Next: 12.7 Kurvendiskussion Up: 12. Übungsbeispiele Previous: 12.5 Logische Indizierung Contents
Anzufertigen sind die MATLAB-Funktionen reihe und eulernum. Die Funktion reihe löst die Reihenentwicklung einiger Funktionen, und die Funktion eulernum berechnet die Eulerschen Zahlen, die für eine spezielle Reihe notwendig sind.
Darüber hinaus benötigt man ein MATLAB-Skript uebreihe, welches die Funktionen testet und die Ergebnisse in einfachen Plots darstellt. Exemplarische Plots sind nach der Beschreibung der Übung eingefügt.
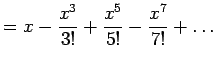 |
(12.7) | |
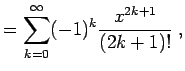 |
(12.8) |
In allen numerischen Programmiersprachen kann man solche unendlichen Reihen natürlich nur näherungsweise auswerten, da die Summation von unendlich vielen Termen unendlich lange dauern würde. Daher gibt man sich mit der endlichen Teilsumme
Summen dieser Art kann man in MATLAB sehr gut ohne die Verwendung von for-Schleifen programmieren. Nützlich sind dabei folgende Informationen:
x = [-2:2]; k = [0:5]; [xx,kk] = meshgrid(x,k);erzeugen
A=xx.^(2*kk+1) kann man nun z.B. f*A) für alle
Werte von Der Aufruf der MATLAB-Funktion reihe soll folgendermaßen aussehen
[r,u,a] = reihe(typ,x,n)wobei typ eine Schaltvariable (switch), x ein Array von
Alle Outputwerte müssen die gleiche Größe wie ![]() haben. Dazu merkt man sich
am Anfang des Programms die Größe von
haben. Dazu merkt man sich
am Anfang des Programms die Größe von ![]() (size), macht aus dem
Array
(size), macht aus dem
Array ![]() einen Vektor (colon). Am Ende des Programms kann man dann
mit reshape
sicherstellen, dass die richtige Größe zurückgegeben
wird.
einen Vektor (colon). Am Ende des Programms kann man dann
mit reshape
sicherstellen, dass die richtige Größe zurückgegeben
wird.
typ='sin'). Für
Stellen Sie mit Hilfe des Skripts uebreihe einen Vergleich zwischen
der Teilsumme der Reihe und der Funktion für verschiedene Werte von ![]() dar.
dar.
'geom' den Wert r der
geometrischen Reihe 12.13, in a den analytischen
Wert aus 12.13 und in u den Wert der unendlichen
Reihe 12.14. Die Fallunterscheidungen können Sie mit
Hilfe der logischen Indizierung durchführen.
Probieren Sie in uebreihe das Konvergenzverhalten aus und stellen Sie die Ergebnisse für r, a und u gemeinsam als Funktion von x dar.
'sechasymp'.
Geben Sie in r die Werte der Teilsumme, in u die Werte der Funktion sech und in a einen Vektor mit NaN zurück.
 |
(12.16) | |
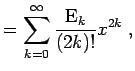 |
(12.17) |
typ='sech'). Außerhalb
des Konvergenzintervalls geben Sie NaN zurück.
Die Eulerschen Zahlen ![]() sind durch folgende Reihe definiert
sind durch folgende Reihe definiert
e = eulernum(k,lmax)berechnet werden sollen. Hier wird nun über
eulernum([0:6]) erhalten.
Vergleichen Sie im Skript uebreihe die Ergebnisse der beiden Reihenentwicklungen und stellen Sie sie graphisch dar.
![\includegraphics[width=0.45\textwidth]{appdata/reihesin}](img587.gif)
![\includegraphics[width=0.45\textwidth]{appdata/reihesech}](img588.gif)
![\includegraphics[width=0.45\textwidth]{appdata/reihegeom}](img589.gif)
Winfried Kernbichler 2005-04-26