Face Recognition
Inhaltsverzeichnis
Introduction
It isn’t difficult to find a lot of literature about face recognition – the improvement of computer calculations opened new possibilities and approaches – therefore a lot of research was done in the last years.
In general, two groups of face recognition algorithms based on the face representation, exist:
- Holistic matching methods: These methods use the whole face region as the raw input to a recognition system. One of the most widely used representations of the face region is the eigenpicture or eigenface, which is based on principal-component analysis.
- Feature based methods: Typically, in these methods, local features such as eyes, nose, and mouth are first extracted and their locations and local statistics (geometric and/or appearance) are fed into a structural classifier.
The so-called “Hybrid-methods” are a combination of the two groups above and use both local features and the whole face region to recognize a face. A machine recognition system should use both, just as the human perception system. One can argue that these methods could potentially offer the best of the two types of methods.[6]
The appearance-based method uses the whole face region as an input to the recognition system. Subspace analysis is done by projecting an image into a lower dimensional subspace formed with the help of training face images. Recognition is performed by measuring the distance between known images and the image to be recognized. The most difficult part of such a system is finding a good subspace. Some well known face recognition algorithms for face recognition are:
- Principal Component Analysis (PCA) [1][2]
- Independent Component Analysis (ICA) [3]
- Linear Discriminant Analysis (LDA) [4] and
- Probalistic neural network Analysis (PNNA) [5].
Also Fourier transformation can be used in recognizing faces.
Implemented Algorithms
2D(1D) Fourier Transformation
The transformation of a picture to frequency-space is quite helpful when comparing patterns or faces. This transformation is done with a 2D Fourier transformation with the in Matlab implemented method fft2. It is interesting that a main part of the information about a pattern on the picture is in the lower frequencies.
After a database of known faces are transformed into frequency-space, the variances for the real and the imaginary part have to be calculated. The frequencies with the higher variances are saved, because they are the most helpful ones when comparing the faces. Another advantage of not using all frequencies is that the training data is reduced - memory/CPU time is saved.
It is also possible to use just the 1D Fourier Transformation to get good results with higher speed. In the following pictures a face is shown after transforming into Fourier-space (1D), cutting off some frequencies and transforming back:
 Picture with all (4096) frequencies
Picture with all (4096) frequencies
 Picture with 4000 frequencies
Picture with 4000 frequencies
 Picture with 2000 frequencies -----
Picture with 2000 frequencies -----
 Picture with 500 frequencies
Picture with 500 frequencies
 Picture with 30 frequencies
Picture with 30 frequencies
With the last picture (30 frequencies) a lot of faces were recognized during our tests.
In [7] it was found, that 22 real and 8 imaginary frequencies are enough for correct classification of faces.
PCA-Method using Eigenfaces
The already mentioned PCA-method was used for face recognition by Turk and Pentland in [8]. They used in their method so-called Eigenfaces for recognition, this system based on the Principal-Component-Analysis (PCA). PCA is a method to reduce the dimension of the vector space of the pictures. Usually all images can be seen as vectors in a vector space with dimension width*height (of the pictures). With PCA the eigenvectors of the covariance-matrix are calculated and the original pictures are described with them as good as possible. In this case the eigenvectors are the "principal components".
The following steps are important when using this method:
- The mean value of all the faces (N*N pixels) in the database has to be determined
- The dimension of the vectorspace is now N*N, therefore it's an intractible problem to get the eigenvectors.
- If M<N^2 there are only M-1 important eigenvectors, which can be easily determined.
- The weights of the pictures in the database have to be determined.
- The Eigenvectors and the weights of the given set of faces have to be saved
- When a new face should be classified it has to be approximated with the given eigenvectors.
- The resulting weights are compared with the weights of the given faces.
For more information see [1],[2] and [8].
The following pictures show two faces and one resulting Eigenface:
Fisher's Linear Discriminant (Fisherfaces)
This method is only useful if more than one face-picture of a given person exists. Influences of the illumination and of facial expressions can be reduced using this method, which is comparable with the Eigenface-method.
For details see [11].
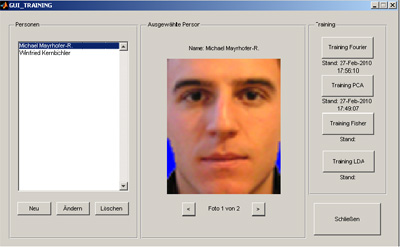
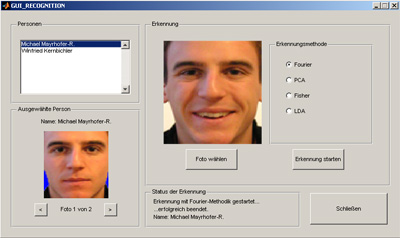
GUI
For an easier user interaction with the programs a GUI was implemented. There are different interfaces for the training and the recognition system:
Tests
References
- [1] I. T. Jolliffe: Principal Component Analysis, 2nd edition. New York, Springer-Verlag, 2002.
- [2] M. Turk and A. Pentland: Face Recognition using Eigenfaces, Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Maui, Hawaii: 586-591, 1991.
- [3] P. C. Yuen and J. H. Lai: Independent Component Analysis of Face Images. IEEE workshop on Biologically Motivated Computer Vision, Seoul, 2000.
- [4] K. Etemad and R. Chellappa: Discriminant Analysis for recognition of human face images. Journal of the Optical Society of America A, 4(8): 1724–1733, 1997
- [5] S. Haykin: Neural Networks, A Comprehensive Foundation, Macmillan, New York, NY, 1994.
- [6] Wenyi Zhao, Rama Chellappa: Face Processing, Elsevier, Amsterdam, 2006.
- [7] H. Spies: Face Recognition - a novel technique, Department of Applied Computing, University of Dundee, Master thesis
- [8] M. Turk, A. Pentland: Eigenfaces for recognition, Journal of Cognitive Neuroscience, 3(1), pp 71-86, 1991
- [9] Lex, Elisabth: Robuste Gesichtserkennung Masterarbeit TU Graz, 2007
- [10] Nikunj, Kela et al: Illumination Invariant Elastic Bunch Graph Matching for Efficient Face Recognition
- [11] Belhumeur et al: Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection, IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 19, NO. 7, JULY 1997