Optimaler Guillotine Zuschnitt
Inhaltsverzeichnis
Allgemeines
Schnittoptimierung ist ein großes Themengebiet mit einer breiten Anwendung. z.B. Holz, Glas, Textilindustrie. Bei reinen Rechtecksproblemen unterscheidet man Guillotine-Schnitt und Nicht-Guillotine-Schnitt. 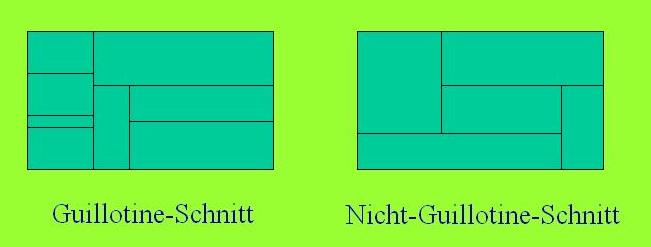
Optimierung
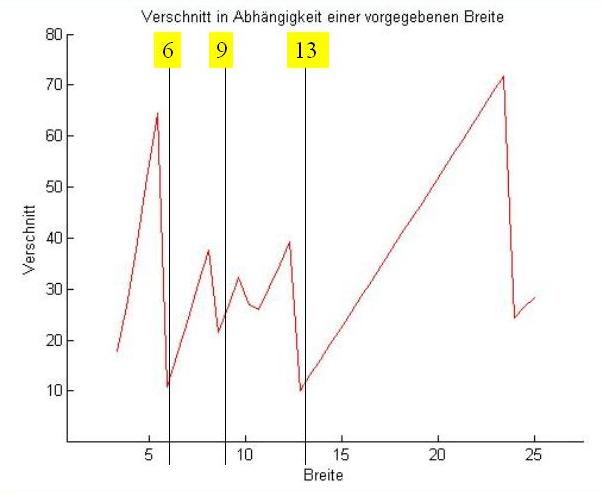
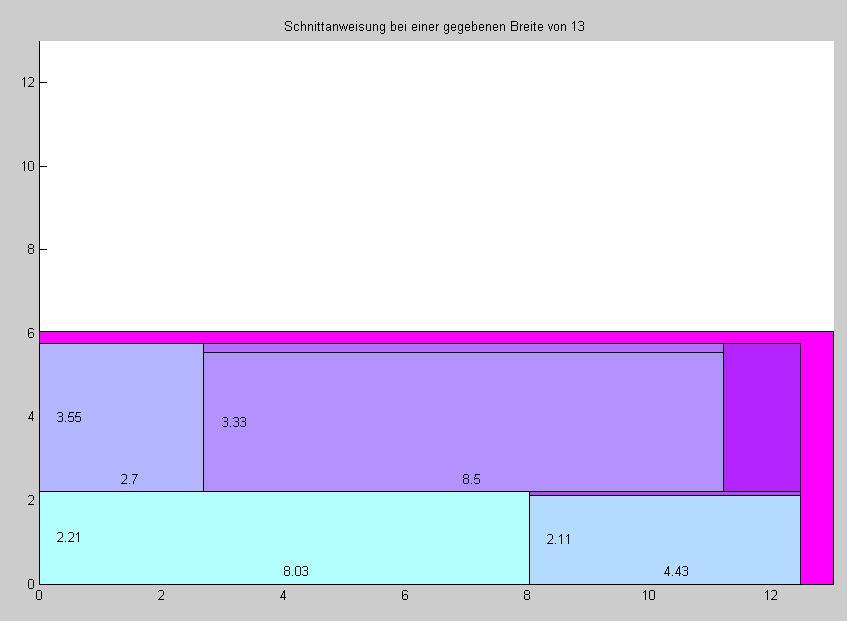
Wichtig ist je nach Anwendung herauszufinden nach welchem konkrten Kriterium optimiert werden soll. In meinem Fall optimiere ich bei gegebener Breite die Länge. D.h. Die Eingabeparameter sind: Länge/Breite der kleinen Rechtecke, Breite des Stücks aus dem ausgeschnitten werden soll. Die Ausgabe ist der Verschnitt, eine grafische Schnittanweisung, die minimal mögliche Länge.
Ansatz
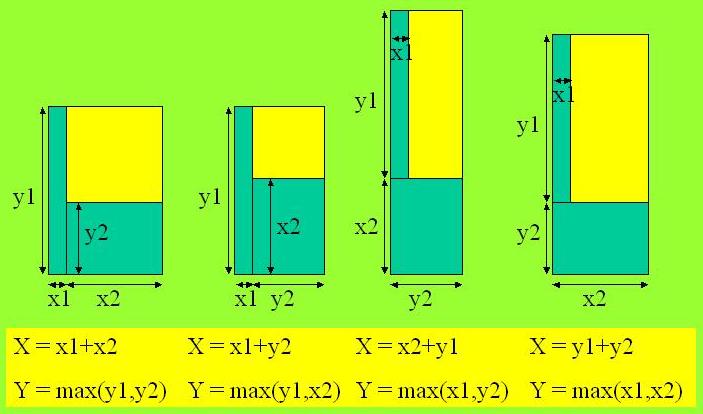
Der programmiertechnische Ansatz beim Guillotineschnitt ist immer zwei und zwei kleine Rechtecke „zusammenkleben“. Dafür gibt es exakt 4 Möglichkeiten.
praktische Umsetzung
Bei jedem Schritt werden aus 2 kleinen Rechtecken ein Großes, wobei eine Optimierung vorgenommen wird, indem aus den 4 Möglichkeiten das kleinste ausgewählt wird und dies bei allen Kombinationsmöglichkeiten der kleinen Rechtecke. Die Randbedienung lautet dabei, nicht breiter als eine die Eingabe zu werden und nicht länger als nötig.
Beispiel
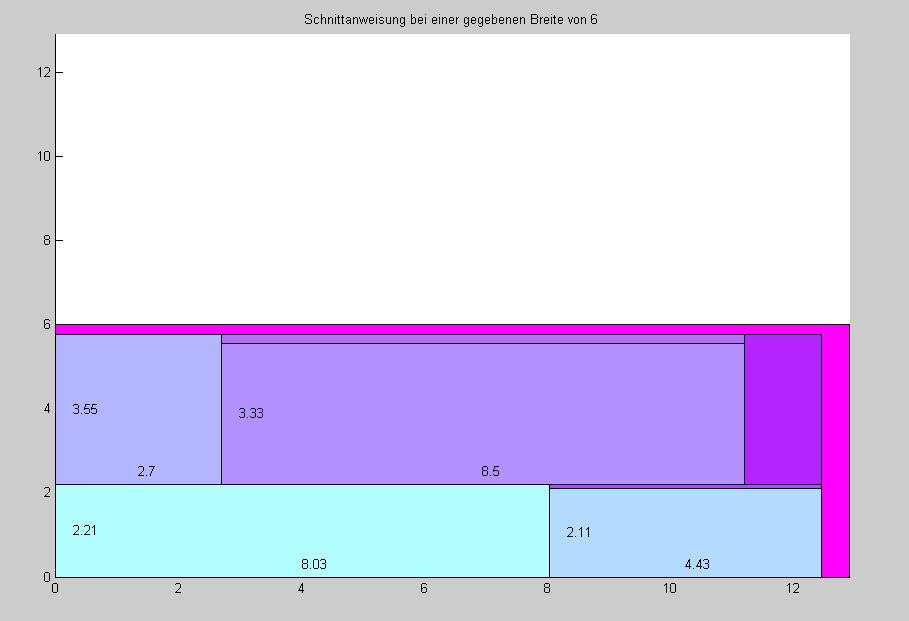
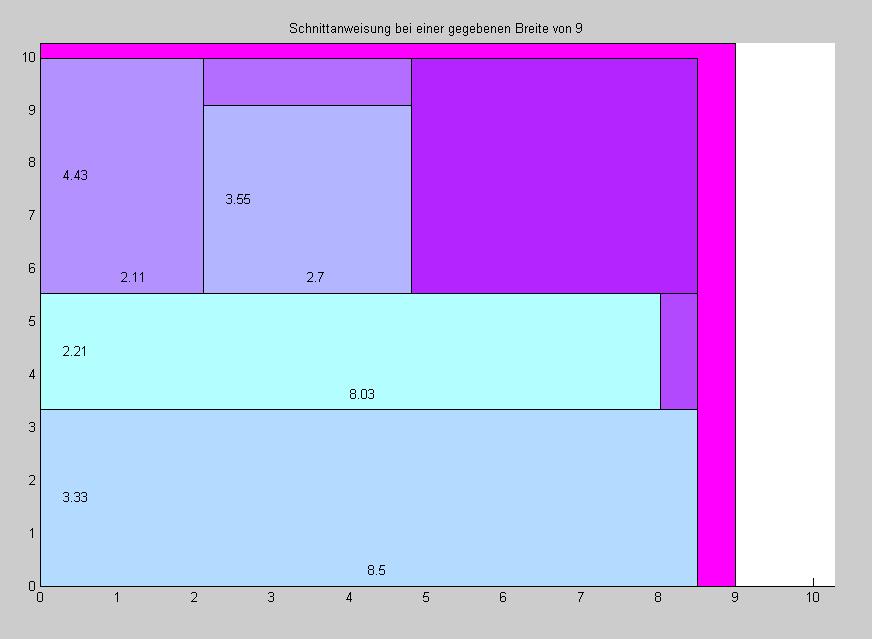
4 kleine Rechtecke werden ausgewertet nach Verschnitt bei verschiedenen Breiten. (x,y): (4.43,2.11),(8.50,3.33), (2.21,8.03), (3.55,2.70)
Literatur
Guntram Scheithauer; "Zuschnitt- und Packungsoptimierung"; ISBN 978-3-8351-0215-6; Vieweg + Teubner Verlag
Fritsch Andreas; "Verschnittoptimierung durch iteriertes Matching" Diplomarbeit im Studiengang Diplom Mathematik; Universität Osnabrück