12.4 Felder

Ziel:

Ziel der Übung ist die Verwendung grundlegender Befehle zum Erstellen und Verändern von Arrays und das Üben der Doppelpunkt Notation für den Zugriff auf Arrays.

Anzufertigen ist eine MATLAB-Funktion arrtest, die die Lösungen für alle Unterbeispiele enthalten soll. Diese werden beim Aufruf durch die Übergabe einer Stringvariablen sw ausgewählt.

Voraussetzung:

Die Eigenschaften von Arrays und von Funktionen, die Arrays erzeugen bzw. verändern werden im Kapitel 3 erklärt. Die Basiseigenschaften werden dort in Tabelle3.1 zusammengefasst, während Befehle zum Erzeugen von Matrizen in den Tabellen 3.3 und 3.4 dargestellt sind. Befehle zum Verändern von Matrizen findet man im Abschnitt 3.5.

Der Zugriff auf Teile von Arrays wird wir im Abschnitt 3.6 erläutert, wobei man im Abschnitt 3.6.2 ausführliche Beispiele findet.

Basiswissen über dieses Kapitel des Skriptums ist unbedingte Voraussetzung für die Übung. Probieren Sie daher u.a. die Befehle zeros, ones, eye, diag aus, und versuchen Sie mit der Doppelpunkt Notation auf Teile der Matrizen zuzugreifen.

Der Aufruf der Funktion sollte mit r = arrtest(sw,m,n,o) erfolgen, wobei sw als Schalter für die einzelnen Subaufgaben dient, m, n und o erfüllen je nach Unterbeispiel unterschiedliche Aufgaben und haben auch jeweils andere Defaultwerte.

Um das Setzen der Defaultwerte in den Unterbeispielen zu erleichtern, sollen am Beginn des Programms nicht übergebene Parameter (nargin) auf den Wert [] (leeres Array) gesetzt werden. Dann kann man innerhalb der switch-Kosntruktion mit Hilfe des Befehls isempty die eigentlichen Defaultwerte setzen.

1. Erzeugen Sie z.B. ein $m \times n$-Array (Default $3 \times 4$) mit lauter gleichen Zahlen (Default o=3). Für den Schalterwert sollte 'const' verwendet werden.

2. Mit dem Schalterwert 'chess' soll eine schachbrettartige Anordnung von Einsern und Nullen als Symbole für schwarz und weiß erzeugt werden. Die Defaultgröße der $m \times n$-Matrix sollte $8 \times 5$ sein und sie sollte links oben mit einer Eins beginnen.

   Denken Sie dabei an die Verwendung der Befehle eye und repmat. Praktisch ist auch der Befehl ceil und das Löschen von ganzen Zeilen oder Spalten mit Hilfe der Zuweisung eines leeren Arrays [], bzw. der Zugriff auf einen Teil der Matrix mit Hilfe der Doppelpunkt Notation.

3. Studieren Sie den Befehl diag und erzeugen Sie dann für den Schalterwert 'diag' mit Hilfe der Befehls diag folgende Matrix mit m=8 Zeilen und n=7 Spalten (Defaultwerte)
   $$r = \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 2 & 0 & 0 &... ...\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 2 & 0 & 0 & 2 & 0 & 0 \end{bmatrix} \; .$$
   Die Einheitszelle sollte dabei allgemein von 1 bis o reichen,
   $$\begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 0 & 2 & 0 & \dots & 0 \... ...\vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & o \end{bmatrix} \; ,$$
   wobei als Defaultwert für o=3 verwendet werden soll.

4. Erstellen Sie für den Schalterwert 'diagplus' eine $m \times m$-Matrix mit einem Defaultwert m = 5.
   $$r = \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 1 & 1 & 1 \\ 1 & 1 & 3 & 1 & 1 \\ 1 & 1 & 1 & 4 & 1 \\ 1 & 1 & 1 & 1 & 5 \end{bmatrix} \; .$$
   Die Werte in der Diagonale sollten immer von 1 bis m laufen. Die restlichen Werte der Matrix sollten den Wert von n haben, wobei der Defaultwert 1 ist.

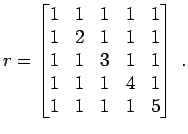
5. Erstellen Sie für den Schalterwert 'randsym' eine $m \times m$-Matrix (Default 5) mit Zufallszahlen im Intervall $\left[0,\; 1\right]$, die zusätzlich symmetrisch ist. Als symmetrische Matrix bezeichnet man eine Matrix für die $a_{ij}=a_{ji}$. Verwenden Sie dazu die Befehle rand, triu und transpose.

   Die Lösung dieses Problems ist ein wenig schwieriger und erfolgt in zwei Stufen. Die erste Stufe erzeugt mit rand und triu eine Matrix, bei der nur der Teil über und inklusive der Hauptdiagonale besetzt ist. In einer zweiten Stufe wird dann die zweite Form des Befehls triu(A,k) verwendet, das Ergebnis transponiert und zum ersten Teil addiert.

   Wie immer gibt es natürlich auch hier andere Lösungen.

6. Erzeugen Sie für die Schalterstellung 'magic' mit dem Befehl magic ein $m \times m$ magisches Quadrat M, wobei $m=5$ ist. Beweisen Sie durch Anwendung der Befehle sum, diag und fliplr, dass alle Summen über die Reihen, die Spalten und die beiden Diagonalen gleich groß sind.

   Verwenden Sie dazu die verschiedenen Formen von sum(M,k) und die Befehle diag und fliplr.

   Verbinden Sie die vier Summenvektoren zu einem Zeilenvektor und bedenken Sie dabei, dass die Ausrichtung der resultierenden Vektoren von sum(M,1) und sum(M,2) unterschiedlich ist.

   Das Zusammenhängen von Arrays erfolgt mit dem Befehl cat bzw. mit seiner Kurzform [A,B] oder [A;B].

   Geben Sie den Vektor mit allen -Summenwerten als Resultat r zurück. Das magische Quadrat wird von der Funktion nicht zurückgegeben.

7. Erzeugen Sie für die Schalterstellung 'numberst' folgende $m \times n$-Matrix (Default $4 \times 6$)
   $$r = \begin{bmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 7 & 8 & 9 & 10 & 1... ...vdots & \vdots \\ 19 & \dots & \dots & \dots & m n -1 & m n \end{bmatrix}\; ,$$
   Erzeugen Sie dabei einen Vektor und verwenden Sie dann die Befehle reshape und transpose. Die Erzeugung des Vektors soll mit der Doppelpunkt Notation erfolgen.

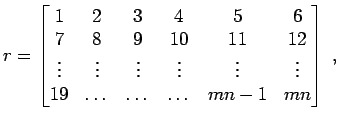
8. Erzeugen Sie mit 'star' folgende Matrix der Größe $2m \times 2m$, wobei als Defaultwert m=3 zu verwenden ist,
   $$r = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 2 & 0 & 0 & 2 ... ... 0 & 0 \\ 0 & 2 & 0 & 0 & 2 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \; .$$

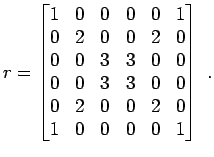
9. Erzeugen Sie mit der 'rstar' folgende Matrix der Größe $2m-1 \times 2m-1$, wobei als Defaultwert m=3 zu verwenden ist,
   $$r = \begin{bmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 2 & 0 & 2 & 0 \\ ... ...& 3 & 0 & 0 \\ 0 & 2 & 0 & 2 & 0 \\ 1 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \; .$$

10. Erzeugen Sie mit der Schalterstellung 'setnan' folgende Matrix der Größe $m \times n$ (Defaultwert $5 \times 6$),
    $$r = \begin{bmatrix} nan & 1 & 1 & 1 & 1 & nan \\ 1 & nan & nan ... ... & nan & nan & nan & nan & 1 \\ nan & 1 & 1 & 1 & 1 & nan \end{bmatrix} \; .$$

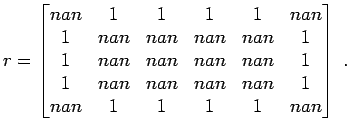
    Beginnen Sie mit einer Matrix mit lauter Einsen und setzen Sie dann mit Hilfe der Doppelpunkt-Notation in zwei Befehlszeilen einmal die Eckpunkte und dann den Mittelbereich auf nan. Dabei ist immer das Keyword end zu verwenden. Der Wert nan symbolisiert in MATLAB ''Not a Number''. Mit nan kann man immer weiterrechnen, wobei die Rechenregel ganz einfach ist. Jede Operation mit nan gibt wieder nan.

Hier noch Anregungen für Studenten mit etwas fortgeschrittenem Interesse:

1. Man kann ganz einfach einen Schalterwert 'test' erstellen, wo die Funktion arrtest sich immmer wieder für alle Fälle aufruft. Dafür erzeugt man eine Zelle
   testcases = {'const','chess','diag', .... };
   und ruft in einer for-Schleife von 1 bis length(testcases)
   arrtest(testcases{k},m,n,o)
   und gibt z.B. in diesem Fall die Resultate mit disp aus.
2. Auf ähnliche Weise kann man auch einen Fall 'in' erstellen, der den Benutzer nach den Werten für sw, m, n und o fragt (input) und dann damit wiederum arrtest aufruft.

In solchen Fällen kann auch eine Ausgabe am Schirm aus einer Funktion, bzw. die zuätzliche Eingabe von Werten mit input interessant sein. Viel Spaß beim Ausprobieren.