Subsections
12.3 Spiralen, Schwebung, Gaußverteilung
- Ziel:
- Umgang mit Funktionen. Setzen von Defaultwerten für
Inputparameter. Erstellen einfacher Plots.
- Vorraussetzung:
- Grundlagen von Funktionen in MATLAB.
Erstellen Sie ein Skript sfunk.m, das alle folgenden Funktionen testet
und einfache Kurven der Funktionen erstellt. Erklärungen zu den Plotbefehlen
finden Sie in dem Abschnitt 11.2.1 bzw. in der MATLAB-Hilfe
für plot.
Defaultwerte kann man setzen, indem man die Anzahl der Input-Variablen
überprüft. Dafür steht nach dem Aufruf der Funktion die Variable
nargin
zur Verfügung. Darüberhinaus bietet sich auch die
Funktion isempty
an. Erklärungen dafür finden Sie in dem
Abschnitt 7.1.6.
12.3.1 Spiralen
Schreiben Sie eine MATLAB-Funktion spirale1, die mit dem Aufruf
[x,y] = spirale1(t,nu,a1,a2)
folgende Funktion berechnet
wobei 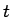 ein Zeitvektor ist. Der Defaultwert für die Frequenz
ein Zeitvektor ist. Der Defaultwert für die Frequenz 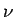 soll
soll 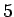 sein und für
sein und für 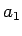 und
und 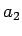 sollen als Defaultwert
sollen als Defaultwert 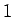 gesetzt werden.
Erzeugen Sie im zugehörigen Testskript sfunk einen vernünftigen
Zeitvektor und plotten Sie
gesetzt werden.
Erzeugen Sie im zugehörigen Testskript sfunk einen vernünftigen
Zeitvektor und plotten Sie 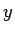 als Funktion von
als Funktion von  , bzw.
, bzw.  und
und 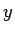 als
Funktion von
als
Funktion von 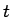 .
.
Schreiben Sie eine MATLAB-Funktion spirale2, die mit dem Aufruf
[x,y] = spirale2(t,nu,a1,a2)
folgende Funktion berechnet
wobei 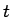 ein Zeitvektor ist. Der Defaultwert für die Frequenz
ein Zeitvektor ist. Der Defaultwert für die Frequenz 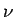 soll
soll 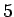 sein und für
sein und für 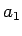 und
und 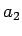 sollen als Defaultwert
sollen als Defaultwert 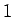 gesetzt werden. Erzeugen Sie im Skript einen vernünftigen Zeitvektor und
plotten Sie
gesetzt werden. Erzeugen Sie im Skript einen vernünftigen Zeitvektor und
plotten Sie 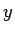 als Funktion von
als Funktion von  , bzw.
, bzw.  und
und 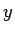 als Funktion von
als Funktion von 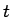 .
.
12.3.2 Schwebung
Schreiben Sie eine MATLAB-Funktion schwebung, die mit dem Aufruf
[x,y] = schwebung(t,nu1,nu2,a1)
folgende Funktion berechnet
wobei 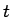 ein Zeitvektor ist. Die Defaultwerte für die Frequenz
ein Zeitvektor ist. Die Defaultwerte für die Frequenz 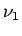 und
und
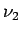 sollen
sollen 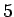 und
und 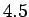 sein. Der Defaultwert für für
sein. Der Defaultwert für für 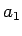 soll
soll 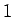 sein. Erzeugen Sie im Skript einen vernünftigen Zeitvektor und plotten Sie
sein. Erzeugen Sie im Skript einen vernünftigen Zeitvektor und plotten Sie
 und
und 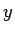 als Funktion von
als Funktion von 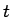 , bzw.
, bzw. 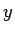 als Funktion von
als Funktion von  . Der
Zeitvektor sollte so gewählt werden, dass man das Phänomen der Schwebung
erkennen kann. Die Darstellung
. Der
Zeitvektor sollte so gewählt werden, dass man das Phänomen der Schwebung
erkennen kann. Die Darstellung 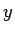 als Funktion von
als Funktion von  nennt man eine
Lissajous-Figur. Die Kurve schließt sich zum ersten Mal, wenn
nennt man eine
Lissajous-Figur. Die Kurve schließt sich zum ersten Mal, wenn 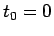 und
und
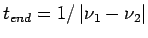 ist.
ist.
12.3.3 Gaußverteilung
In der Wahrscheinlichkeitsrechnung und auch in der Physik hat die
Normalverteilung bzw. Gaußverteilung eine große Bedeutung. Sie ist definiert
durch
wobei 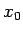 und
und 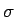 die Parameter der Verteilung sind. In
die Parameter der Verteilung sind. In 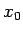 liegt sowohl das Maximum als auch das Symmetriezentrum, und
liegt sowohl das Maximum als auch das Symmetriezentrum, und 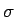 ist
der Abstand von diesem Zentrum zu den Wendepunkten. Wie für jede
Wahrscheinlichkeitsverteilung gilt
ist
der Abstand von diesem Zentrum zu den Wendepunkten. Wie für jede
Wahrscheinlichkeitsverteilung gilt
In der Physik verwendet man häufig auch eine Summation über mehrere
Gaußfunktionen mit jeweils unterschiedlichen Parametern. Dies hat den Sinn,
dass man gleichzeitig mehrere Maxima darstellen kann. Allgemein kann man
die Funktion dann definieren als
wobei 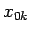 und
und 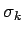 die gleiche Bedeutung wie vorher haben. Die
Summation erfolgt über alle
die gleiche Bedeutung wie vorher haben. Die
Summation erfolgt über alle 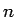 Werte der Parameter
Werte der Parameter 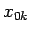 und
und 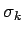 .
.
Schreiben Sie eine MATLAB-Funktion gauss1d, die mit folgendem Aufruf
g(x) = gauss1d(x,x0,sigma)
die Gaußverteilung als Funktion des Vektors  berechnet. Setzen Sie die
Defaultwerte
berechnet. Setzen Sie die
Defaultwerte
![$ x_{0}=[-1,1]$](img497.gif) und
und
![$ \sigma=[0.5,1]$](img498.gif) .
.
- Initialisieren Sie
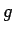 als Feld mit lauter Nullen in der Größe von
als Feld mit lauter Nullen in der Größe von
 .
.
- Um sicherzustellen, dass die Vektoren für
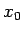 und
und 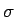 gleich
lang sind, kann man deren Länge (length) vergleichen und bei
unterschiedlicher Länge einen Fehler (error) melden.
gleich
lang sind, kann man deren Länge (length) vergleichen und bei
unterschiedlicher Länge einen Fehler (error) melden.
- Bilden Sie die Summe über alle Werte (
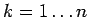 ) der Parameter mit
Hilfe einer einzigen for-Schleife. Vergessen Sie dabei nicht,
dass
) der Parameter mit
Hilfe einer einzigen for-Schleife. Vergessen Sie dabei nicht,
dass  ein Array sein kann.
ein Array sein kann.
Hinweis: Eine for-Schleife hilft bei der Summation über
die einzelnen Beiträge zur Summe 12.3.3. Dabei ist es
praktisch, wenn man noch vor der Schleife ein Feld erzeugt, das gleich
groß ist, wie die Inputvariable x, das aber lauter Nullen
enthält. Der sinnvollste Befehl dafür ist:
g = zeros(size(x))
Dann kann man in der Schleife
g = g + ...
schreiben und bei jedem Durchlauf werden die Werte für einen Peak
addiert. Nach dem Ende der Schleife muss man durch die Anzahl der Peaks
n, also durch die Länge des Vektors x0 (oder sigma)
dividieren. Damit ist dann die Normierung auch bei mehreren Peaks
sichergestellt.
- Probieren Sie die Funktion mit Hilfe des Skripts sfunk
aus und machen Sie einen Plot
plot(x,g)
Wählen Sie den  -Vektor in einem vernünftigen Bereich, damit die
Funktion
-Vektor in einem vernünftigen Bereich, damit die
Funktion 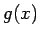 sinnvoll dargestellt wird
(linspace). Beschriften Sie den Plot mit Achsenbeschriftung und
Titel.
sinnvoll dargestellt wird
(linspace). Beschriften Sie den Plot mit Achsenbeschriftung und
Titel.
![\includegraphics[width=0.45\textwidth]{appdata/gauss}](img503.gif)
Winfried Kernbichler
2005-04-26
![\includegraphics[width=0.45\textwidth]{appdata/spirale}](img480.gif)
![\includegraphics[width=0.45\textwidth]{appdata/schwebung}](img488.gif)
![\includegraphics[width=0.45\textwidth]{appdata/schwebungxy}](img489.gif)
![\includegraphics[width=0.45\textwidth]{appdata/gauss}](img503.gif)