Unterabschnitte
Wenn in einem System ein Teil aus der Ruhelage, z.B. durch einen
Stoß, etwas herausgeschoben wird, dann treten meist Kräfte auf, die diesen
in die Ruhelage (E. equilibrium position) zurücktreiben. Auf grund der
Trägheit der Masse dieses Teiles bleibt dieser aber nicht in der Ruhelage
stehen, sodern schießt darüber hinaus. Dabei wachsen die rücktreibenden
Kräfte wieder so an, daß diese Masse wieder umkehrt. Somit kommt es zu
Schwingungen um die Ruhelage. Wenn auch Reibung vorhanden ist, wird dieser
Schwingungsvorgang früher oder später zur Ruhe kommen (gedämpfte Schwingung,
E. damped oscillation). Im Idealfall, daß keine Reibung vorhanden ist,
kommt es zu einer ungedämpften Schwingung.
Oft ist die genaue analytische Form der rücktreibenden Kraft nicht bekannt.
Dann behilft man sich mit Reihenentwicklungen (Taylorreihen) um die Ruhelage,
berücksichtigt aber meist nur einen Teil der Glieder, nämlich nur die niedrigsten
Potenzen. Begnügt man sich mit den linearen Termen, spricht man von einem
harmonischen Oszillator (E. harmonic oscillator); werden auch noch höhere
Potenzen mitgenommen, spricht man von einem anharmonischen Oszillator
(E. anharmonic oscillator). Dies sind die einfachsten und
wichtigsten Modelle für Schwingungen. Selbst wenn die Kraft genau bekannt ist,
ist es oft zweckmäßig mit den gerade beschriebenen Näherungen zu arbeiten.
Wirkt keine äußere Kraft, heißt der Oszillator frei (E.: free oscillator).
Wirkt noch eine zusätzliche äußere (meist zeitabhängige) Kraft, dann kommt
es zu erzwungenen Schwingungen und dabei kann Resonanz auftreten. In diesem
Fall ist es besonders wichtig, die Reibung zu berücksichtigen.
Die gerade zuvor besprochene Reihenentwicklung der rücktreibenden Kraft wird
hier am eindimensionalen Fall erklärt. Die Kraft sei eine Funktion der
Koordinate 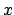 , also
, also 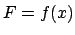 .
. 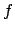 wird nun in eine Taylorreihe um
wird nun in eine Taylorreihe um
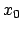 entwickelt:
entwickelt:
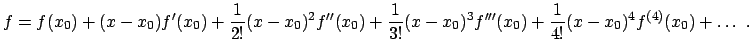 |
(41) |
Weil 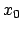 die Koordinate der Gleichgewichtslage ist, sind dort die auf die
Masse
die Koordinate der Gleichgewichtslage ist, sind dort die auf die
Masse 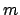 wirkenden Kräfte im Gleichgewicht, die resultierende Kraft ist Null,
wirkenden Kräfte im Gleichgewicht, die resultierende Kraft ist Null,
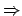
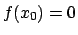 .
. 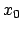 sei eine stabile Gleichgewichtslage: Die
Kräfte, die bei einer Entfernung der Masse aus der Gleichgewichtslage wirksam
werden, wollen die Masse in die Gleichgewichtslage zurücktreiben. Dazu muß gelten:
sei eine stabile Gleichgewichtslage: Die
Kräfte, die bei einer Entfernung der Masse aus der Gleichgewichtslage wirksam
werden, wollen die Masse in die Gleichgewichtslage zurücktreiben. Dazu muß gelten:
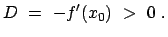 |
(42) |
Wenn vorläufig die höheren Terme in der Entwicklung (4.1) vernachläßigt
werden, dann lautet die Kraft:
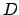 heißt die Direktionskraft. Die Skala auf der
heißt die Direktionskraft. Die Skala auf der 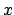 -Achse wird nun so gewählt,
daß der Gleichgewichtspunkt der Nullpunkt ist, also
-Achse wird nun so gewählt,
daß der Gleichgewichtspunkt der Nullpunkt ist, also
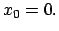 Damit haben wir
folgenden Ausdruck für die Kraft und die Bewegungsgleichung:
Damit haben wir
folgenden Ausdruck für die Kraft und die Bewegungsgleichung:
Division durch 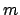 und Einführung der Abkürzung
und Einführung der Abkürzung 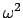 machen aus
der obigen Bewegungsgleichung die Differentialgleichung:
machen aus
der obigen Bewegungsgleichung die Differentialgleichung:
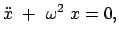 mit mit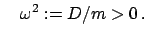 |
(43) |
Dies ist eine Schwingungsgleichung. In diese wird folgender Ansatz
für die Lösungsfunktion 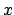 eingesetzt:
eingesetzt:
Diese Identität soll für alle Zeiten (eines gewissen Zeitintervalls) gelten;
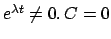 ergäbe nur die triviale Lösung (
ergäbe nur die triviale Lösung (
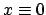 ), diese ist uninteressant. Es muß daher gelten:
), diese ist uninteressant. Es muß daher gelten:
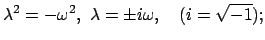 |
|
|
|
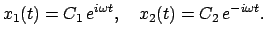 |
|
|
(44) |
In der Vorlesung über Differentialgleichungen wird gezeigt, daß diese beiden
Funktionen ein
Fundamentalsystem bilden und daher die allgemeine Lösung eine Linearkombination
von
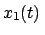 und
und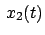 ist:
ist:
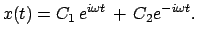 |
(45) |
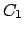 und
und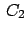 sind willkürliche Konstanten
sind willkürliche Konstanten
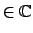 . Für
unser Problem sind nur reelle Lösungen von Bedeutung, wir formen daher um
mittels der Eulerschen Identität:
. Für
unser Problem sind nur reelle Lösungen von Bedeutung, wir formen daher um
mittels der Eulerschen Identität:
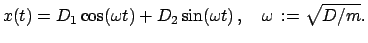 |
(46) |
Die allgemeine Lösung kann noch in anderer Form geschrieben werden,
nämlich als:
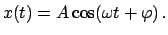 |
(47) |
Der Übergang zwischen beiden Schreibweisen erfolgt auf folgende Weise:
Die Konstanten
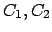 bzw.
bzw.
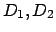 bzw.
bzw.
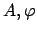 sind aus den Anfangsbedingungen zu bestimmen.
sind aus den Anfangsbedingungen zu bestimmen.
Eine spezielle Anfangsbedingung: 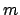 ist aus der Ruhelage herausgezogen worden,
wird nun ausgelassen (Abb. 4.1).
ist aus der Ruhelage herausgezogen worden,
wird nun ausgelassen (Abb. 4.1).
 |
(48) |
Diese Anfangsbedingung wird in die allg. Lösung eingesetzt:
Die spezielle Lösung zur obigen Anfangsbedingung ist:
Abbildung:
Lösung der Schwingungsgleichung bei Elongation aus der Ruhelage.
Links die Lage und der Impuls als Funktion der Zeit.
Rechts oben das Potential, unten das Phasenraumdiagramm. Die Punkte schließen
den Weg innerhalb gleicher Zeitintervalle ein.
|
![\includegraphics[scale=0.93]{k4_schwingungsglg}](img497.gif) |
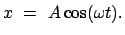 |
(49) |
Die Schwingung kann wie in Abb. 4.1 dargestellt werden. Die Kurven links
geben die Lage 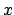 und den Impuls
und den Impuls 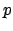 des Massenpunkts
als Funktion der Zeit
des Massenpunkts
als Funktion der Zeit 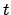 .
.
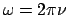 heißt die Kreisfrequenz,
heißt die Kreisfrequenz,
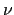 ist die Frequenz,
ist die Frequenz, 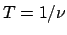 die Schwingungsdauer. Alle diese Größen sind
durch die Direktionskraft
die Schwingungsdauer. Alle diese Größen sind
durch die Direktionskraft 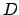 und die Masse
und die Masse 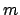 festgelegt.
festgelegt.
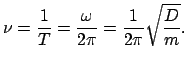 |
(410) |
Zu anderen Anfangsbedingungen ergeben sich auch andere spezielle Lösungen.
Z.B. ergibt sich für die Anfangsbedingung:
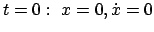 die spezielle Lösung
die spezielle Lösung
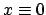 . Wenn der Massenpunkt anfänglich im
Gleichgewichtgspunkt in Ruhe ist, bleibt er es in alle Ewigkeit. - Wird die Masse
aus der Ruhelage gestoßen, gibt dies die Anfangsbedingungen:
. Wenn der Massenpunkt anfänglich im
Gleichgewichtgspunkt in Ruhe ist, bleibt er es in alle Ewigkeit. - Wird die Masse
aus der Ruhelage gestoßen, gibt dies die Anfangsbedingungen:
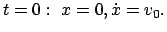 Dies führt zur speziellen Lösung:
Dies führt zur speziellen Lösung:
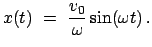 |
(411) |
Wird die Anfangsbedingung ganz allgemein gehalten, nämlich: Am Anfangszeitpunkt
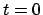 ist die Masse am Punkt
ist die Masse am Punkt 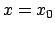 und hat dort die Geschwindigkeit
und hat dort die Geschwindigkeit
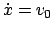 , dann ist die spezielle Lösung:
, dann ist die spezielle Lösung:
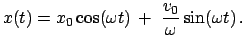 |
(412) |
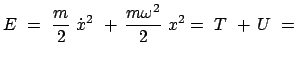 const. const. |
(413) |
Die Konstanz der Gesamtenergie 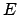 ergibt sich auch wenn man eine der Lösungen
(4.9), (4.11) oder (4.12) in den Energieausdruck einsetzt.
Z.B. liefert (4.9) in den obigen Energieausdruck eingesetzt:
ergibt sich auch wenn man eine der Lösungen
(4.9), (4.11) oder (4.12) in den Energieausdruck einsetzt.
Z.B. liefert (4.9) in den obigen Energieausdruck eingesetzt:
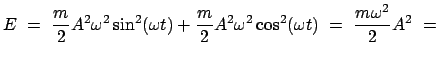 const. const. |
(414) |
Man sieht auch hier, daß 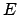 nicht von
nicht von 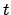 abhängt. Die Gesamtenergie ist proportional
zum Quadrat der Amplitude
abhängt. Die Gesamtenergie ist proportional
zum Quadrat der Amplitude 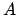 und auch zum Quadrat der Kreisfrequend
und auch zum Quadrat der Kreisfrequend 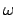 .
Das Potential errät man leicht aus dem Ausdruck für die Gesamtenergie:
.
Das Potential errät man leicht aus dem Ausdruck für die Gesamtenergie:
In Abb. 4.1 ist rechts oben die potentielle Energie 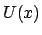 eingezeichnet.
Für eine
gegebene Energie
eingezeichnet.
Für eine
gegebene Energie 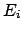 oszilliert der Massenpunkt zwischen den Punkten
oszilliert der Massenpunkt zwischen den Punkten 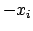 und
und
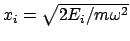 . Dies ergibt sich aus dem Energiesatz. Löst man
Gl. (4.13) nach der Geschwindigkeit
. Dies ergibt sich aus dem Energiesatz. Löst man
Gl. (4.13) nach der Geschwindigkeit 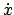 auf, so ergibt sich:
auf, so ergibt sich:
Die Geschwindigkeit muß reell sein; daher darf der Radikand nicht negativ sein.
Diese Bedingung ist zwischen 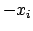 und
und 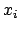 erfüllt; an den beiden Endpunkten
ist der Radikand Null, also die Geschwindigkeit Null; dies sind die Umkehrpunkte.
Im Phasenraumdiagramm, rechts unten in Abb. 4.1, entspricht dieser
Schwingung eine Ellipse mit den Halbachsen
erfüllt; an den beiden Endpunkten
ist der Radikand Null, also die Geschwindigkeit Null; dies sind die Umkehrpunkte.
Im Phasenraumdiagramm, rechts unten in Abb. 4.1, entspricht dieser
Schwingung eine Ellipse mit den Halbachsen 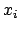 und
und
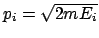 . Aus
Gl. (4.13) erhält man die Gleichung einer Ellipse, wenn man mit der Energie
. Aus
Gl. (4.13) erhält man die Gleichung einer Ellipse, wenn man mit der Energie 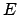 durchdividiert. Gln. (4.9), (4.11) oder (4.12) sind die
Parameterdarstellung einer Ellipse. Der dicke Punkt im Zentrum des Phasendiagramms (und
die tiefste Stelle des Potentials) entsprechen dem in der Gleichgewichtslage ruhenden
Punkt. Während die Masse im realen Raum eine Periode absolviert, durchläuft der
Phasenpunkt seine Phasenbahn (hier die seiner Energie
durchdividiert. Gln. (4.9), (4.11) oder (4.12) sind die
Parameterdarstellung einer Ellipse. Der dicke Punkt im Zentrum des Phasendiagramms (und
die tiefste Stelle des Potentials) entsprechen dem in der Gleichgewichtslage ruhenden
Punkt. Während die Masse im realen Raum eine Periode absolviert, durchläuft der
Phasenpunkt seine Phasenbahn (hier die seiner Energie 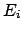 entsprechende Ellipse)
im Uhrzeigersinn. Es gibt nur eine Art von Bewegung, eine Schwingung mit größerer
oder kleinerer Amplitude, je nach den Anfangsbedingungen.
entsprechende Ellipse)
im Uhrzeigersinn. Es gibt nur eine Art von Bewegung, eine Schwingung mit größerer
oder kleinerer Amplitude, je nach den Anfangsbedingungen.
Anharmonische Schwingung
Die Bewegungstypen werden zahlreicher, wenn man in der Entwicklung der Kraftfunktion,
Gl. (4.1), den ersten nichtlinearen Term ( mit 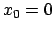 und
und
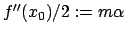 )
hinzunimmt:
)
hinzunimmt:
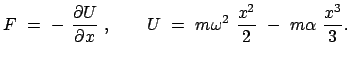 |
(416) |
Abbildung 4.2:
Anharmonische Schwingung. Oben Potential U(x), Gl. (4.16), und verschiedene
Energiewerte. Unten das Phasenraumdiagramm.
|
![\includegraphics[scale=0.67]{k4_anharmschwing}](img530.gif) |
Die zugehörige Bewegungsgleichung kann exakt analytisch mit Hilfe elliptischer
Funktionen und Integrale gelöst werden. Wichtige qualitative und quantitative
Aussagen können bereits aus dem Energiesatz und dem Phasenraumdiagramm gefunden
werden. Das Potential ist in Abb. 4.2 oben eingezeichnet. Sind die
Schwingungsamplitude, damit auch die Gesamtenergie
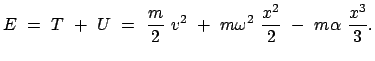 |
(417) |
klein genug, dann schwingt der Massenpunkt zwischen 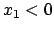 und
und 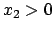 . Diese
beiden Werte ergeben sich wieder aus den Schnittpunkten der horizontalen Geraden
. Diese
beiden Werte ergeben sich wieder aus den Schnittpunkten der horizontalen Geraden 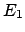 (
(
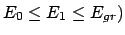 mit der Potentialfunktion U(x). Wegen der unsymmetrischen
Form des Potentials liegen sie nicht symmetrisch zum Ursprung. Die Phasekurve
(
mit der Potentialfunktion U(x). Wegen der unsymmetrischen
Form des Potentials liegen sie nicht symmetrisch zum Ursprung. Die Phasekurve
(
 ) ist geschlossen, es liegt eine anharmonische Schwingung vor.
Das nennt man auch einen gebundenen Zustand.
) ist geschlossen, es liegt eine anharmonische Schwingung vor.
Das nennt man auch einen gebundenen Zustand.
Löst man obige
Gleichung nach der Geschwindigkeit 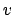 auf, findet man eine Differentialgleichung,
die durch Separation gelöst werden kann:
auf, findet man eine Differentialgleichung,
die durch Separation gelöst werden kann:
Für die Zeit einer halben Periode ergibt sich daraus:
An den Umkehrpunkten ist
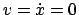 , also die obige Wurzel Null. Der
Integrand ist also dort singulär. Doch ist es eine schwache Singularität
(so wie die von
, also die obige Wurzel Null. Der
Integrand ist also dort singulär. Doch ist es eine schwache Singularität
(so wie die von
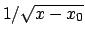 an der Stelle
an der Stelle 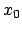 ), der Integrand ist also
integrabel; das obige bestimmte Integral ist endlich.
), der Integrand ist also
integrabel; das obige bestimmte Integral ist endlich.
Für
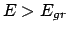 (wie z.B. für
(wie z.B. für 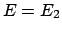 ) kann die Masse nach rechts bis ins
Unendliche laufen (
) kann die Masse nach rechts bis ins
Unendliche laufen (
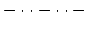 ) .
Ungebunder oder freier Zustand.
Im Bereich
) .
Ungebunder oder freier Zustand.
Im Bereich
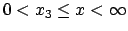 ist der Radikand ebenfalls positiv. Das Teilchen,
damit auch sein Phasenpunkt, können ins Unendliche gelangen (
ist der Radikand ebenfalls positiv. Das Teilchen,
damit auch sein Phasenpunkt, können ins Unendliche gelangen ( ).
Wenn der Massenpunkt einwärts läuft, dann wird er an der Stelle
).
Wenn der Massenpunkt einwärts läuft, dann wird er an der Stelle 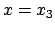 reflektiert und gelangt dann ins Uendliche. Doch ist dieser Bereich vom
physikalischen Standpunkt aus nicht sehr realistisch.
reflektiert und gelangt dann ins Uendliche. Doch ist dieser Bereich vom
physikalischen Standpunkt aus nicht sehr realistisch.
Je näher die Energie 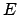 an der Grenzenergie
an der Grenzenergie 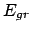 liegt, desto größer wird
der Wert der Periode. Denn bei
liegt, desto größer wird
der Wert der Periode. Denn bei
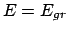 fallen die Nullstellen
fallen die Nullstellen 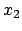 und
und
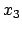 zusammen,
zusammen,
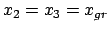 ; unter der Wurzel steht ein quadratischer
Ausdruck
; unter der Wurzel steht ein quadratischer
Ausdruck
 ;
der Integrand in dem obigen Ausdruck für die Periode hat einen Pol 1. Ordnung;
das Integral nimmt den Wert Unendlich an. Das Teilchen kann sich nur von links oder
rechts dem sog. Sattelpunkt nähern, es benötigt unendlich lange Zeit bis es
diesen erreicht ( --- ). Im Phasendiagramm entspricht dieser Bewegung die ausgezogene
Kurve; der Phasenpunkt kann aber immer nur einen Teil eines Astes dieser Kurve
durchlaufen.
Diese Bewegung heißt Limitationsbewegung. Diese Kurve trennt zwei Gebiete
des Phasenraumes, in denen verschiedenartige Bewegungen ablaufen. Deswegen heißt
sie auch Separatrix (E. separatrix).
;
der Integrand in dem obigen Ausdruck für die Periode hat einen Pol 1. Ordnung;
das Integral nimmt den Wert Unendlich an. Das Teilchen kann sich nur von links oder
rechts dem sog. Sattelpunkt nähern, es benötigt unendlich lange Zeit bis es
diesen erreicht ( --- ). Im Phasendiagramm entspricht dieser Bewegung die ausgezogene
Kurve; der Phasenpunkt kann aber immer nur einen Teil eines Astes dieser Kurve
durchlaufen.
Diese Bewegung heißt Limitationsbewegung. Diese Kurve trennt zwei Gebiete
des Phasenraumes, in denen verschiedenartige Bewegungen ablaufen. Deswegen heißt
sie auch Separatrix (E. separatrix).
Harmonischer Oszillator mit Dämpfung
Die Verluste, die z.B. durch Reibung (E.: friction) in der Feder oder in der
Luft verursacht werden, können oft durch eine geschwindigkeitsabhängige
Reibungskraft
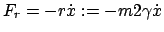 |
(418) |
(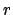 und
und 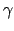 konstant) beschrieben werden. Statt (4.3) erhält man dann die
Schwingungsgleichung
konstant) beschrieben werden. Statt (4.3) erhält man dann die
Schwingungsgleichung
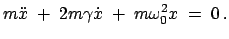 |
(419) |
Mittels Exponentialansatz erhält man die charakteristische Gleichung
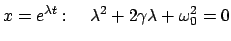 |
(420) |
mit den Wurzeln
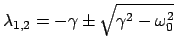 |
(421) |
Wir müssen drei Fälle unterscheiden, je nachdem, ob die Quadratwurzel
imaginär, Null oder reell ist.
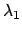 und
und
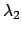 sind zueinander konjugiert komplex. Die
allgemeine Lösung
sind zueinander konjugiert komplex. Die
allgemeine Lösung
beschreibt für 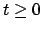 eine gedämpfte Schwingung (E.: damped oscillation).
Für
eine gedämpfte Schwingung (E.: damped oscillation).
Für
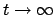 kommt der Oszillator wegen der Reibungsverluste zur Ruhe.
Als Beispiel ist der Fall mit
kommt der Oszillator wegen der Reibungsverluste zur Ruhe.
Als Beispiel ist der Fall mit 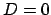 in Abb. 4.3 gezeigt.
in Abb. 4.3 gezeigt.
Abbildung:
Gedämpfte Schwingung: Links die Lagekoordinate über der Zeit.
Rechts das Phasendiagramm. Die Punkte trennen gleiche Zeitintervalle  .
.
|
![\includegraphics[scale=0.83]{k4_gedaempfteschw}](img567.gif) |
Man beachte, daß die Frequenz des gedämpften Oszillators
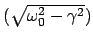 gegenüber der des ungedämpften Oszillators
gegenüber der des ungedämpften Oszillators
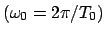 herabgesetzt ist. Die Phasenkurve zieht sich allmählich auf den Ursprung zusammen,
wobei die Schwingung immer langsamer wird.
herabgesetzt ist. Die Phasenkurve zieht sich allmählich auf den Ursprung zusammen,
wobei die Schwingung immer langsamer wird.
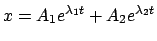 |
(423) |
Die Reibung ist so stark, daß überhaupt keine Schwingung möglich ist, sondern
der Oszillator in seine Ruhelage zurückkehrt. Dies verläuft entweder überhaupt
monoton oder der Massenpunkt durchquert einmal die Ruhelage (Abb. 4.4).
Abbildung 4.4:
Aperiodische Bewegung, Kriechfall.
|
![\includegraphics[scale=0.88]{k4_aperiodbew}](img572.gif) |
Da die charakteristische Gl. (4.20) für 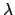 nur eine Lösung hat, muß
man noch eine
zweite linear unabhängige Lösung finden. Man sieht durch Einsetzen, daß in
diesem Fall mit
nur eine Lösung hat, muß
man noch eine
zweite linear unabhängige Lösung finden. Man sieht durch Einsetzen, daß in
diesem Fall mit
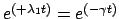 auch
auch
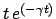 eine Lösung von (4.19) ist.
Auch diese Lösung strebt für
eine Lösung von (4.19) ist.
Auch diese Lösung strebt für
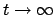 gegen Null. Die allg. Lösung
gegen Null. Die allg. Lösung
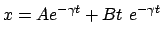 |
(424) |
gibt ähnliche Bewegungsformen wie im vorhergehenden Fall.
Auf den Massenpunkt 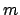 wirkt neben den Federn (oder sonstigen elastischen
Kräften, die ihn in die Ruhelage zurückziehen wollen,
noch eine zusätzliche zeitabhängige Kraft
wirkt neben den Federn (oder sonstigen elastischen
Kräften, die ihn in die Ruhelage zurückziehen wollen,
noch eine zusätzliche zeitabhängige Kraft
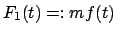 :
:
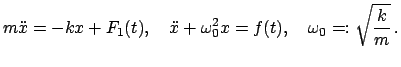 |
(425) |
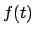 heißt manchmal das Störglied. Es macht aus der homogenen DGl. (4.3)
bzw. (4.19) eine inhomogene Differentialgleichung. Die allgemeine Lösung
der letzteren kann man aus der Summe der allg. Lösung der homogenen Gl. (4.3),
heißt manchmal das Störglied. Es macht aus der homogenen DGl. (4.3)
bzw. (4.19) eine inhomogene Differentialgleichung. Die allgemeine Lösung
der letzteren kann man aus der Summe der allg. Lösung der homogenen Gl. (4.3),
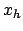 , plus einer partikulären Lösung,
, plus einer partikulären Lösung,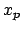 , der inhomogenen (4.25)
aufbauen:
Dies beweist man, indem man zwei partikuläre Lösungen,
, der inhomogenen (4.25)
aufbauen:
Dies beweist man, indem man zwei partikuläre Lösungen,
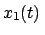 und
und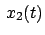 , in obige Gleichung einsetzt
und die resultierenden Gleichungen voneinander abzieht:
, in obige Gleichung einsetzt
und die resultierenden Gleichungen voneinander abzieht:
ist Lösung der homogenen Schwingungsgleichung (4.3).
Die partikuläre Lösung 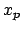 hängt von der Form der Kraft
hängt von der Form der Kraft 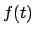 ab.
Besonders wichtig sind periodische Anregungen. Wir betrachten den Sonderfall
einer harmonischen Störkraft der Kreisfrequenz
ab.
Besonders wichtig sind periodische Anregungen. Wir betrachten den Sonderfall
einer harmonischen Störkraft der Kreisfrequenz 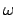 .
.
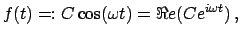 |
(426) |
(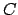 reell, gibt die Stärke der anregenden Kraft). Die obige Einführung des
Realteiles gestattet eine bequeme Rechnung mit komplexen Größen. Wir finden
eine partikuläre Lösung durch den Ansatz
reell, gibt die Stärke der anregenden Kraft). Die obige Einführung des
Realteiles gestattet eine bequeme Rechnung mit komplexen Größen. Wir finden
eine partikuläre Lösung durch den Ansatz
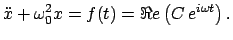 |
(427) |
Einsetzen des obigen Ansatzes in Gl. (4.25) gibt:
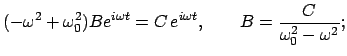 |
|
|
|
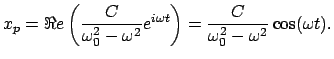 |
|
|
(428) |
Die allgemeine Lösung ist die Überlagerung zweier Schwingungen mit den
Frequenzen 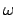 und
und
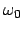 .
.
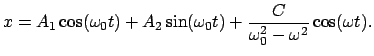 |
(429) |
Die Elongation und der Impuls als Funktion der Zeit haben eine übersichtliche
Form. Das Phasenraumdiagramm wird sehr undurchsichtig, wenn das Frequenzverhältnis
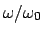 nicht ein einfaches Zahlenverhältnis darstellt
(vgl. Abb. 4.5).
nicht ein einfaches Zahlenverhältnis darstellt
(vgl. Abb. 4.5).
Die Lösung wird unendlich für
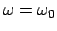 (Resonanz, E.: resonance).
In diesem Fall ist die Reibung so wesentlich, daß sie nicht vernachlässigt
werden darf. Wir betrachten daher die Gleichung
(Resonanz, E.: resonance).
In diesem Fall ist die Reibung so wesentlich, daß sie nicht vernachlässigt
werden darf. Wir betrachten daher die Gleichung
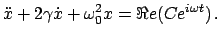 |
(430) |
Wir betrachten wiederum den Schwingfall (s.  4.1.3),
4.1.3),
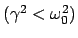 . Wieder erhalten wir eine partikuläre Lösung
der obigen inhomogenen Gleichung durch den Ansatz
. Wieder erhalten wir eine partikuläre Lösung
der obigen inhomogenen Gleichung durch den Ansatz
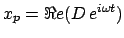 :
:
Die allgemeine Lösung besteht aus
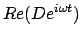 , der partikulären
Lösung von (4.30), und aus der allg. Lösung (4.22)
der homogenen Gleichung (4.19):
, der partikulären
Lösung von (4.30), und aus der allg. Lösung (4.22)
der homogenen Gleichung (4.19):
Man sieht, daß die Lösung der homogenen Gleichung mit zunehmender Zeit
abklingt, sodaß das stationäre (langzeitliche) Verhalten von dem der
partikulären Lösung bestimmt ist. Dies sind man auch aus dem Phasendiagramm,
Abb. 4.6. Die stationäre Lösung 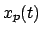 wird daher genauer untersucht.
Diese partikuläre Lösung (2. Zeile von Gl. (4.31)) läßt sich schreiben als
wird daher genauer untersucht.
Diese partikuläre Lösung (2. Zeile von Gl. (4.31)) läßt sich schreiben als
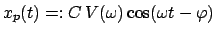 |
(432) |
mit
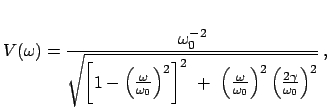 |
(433) |
![$\displaystyle \varphi = \arctan \frac{\omega_{0}^{2} - \omega^{2}}{2 \omega \ga...
...mega_{0}^2}}{\frac{\omega}{\omega_{0}} \frac{2 \gamma}{\omega_{0}}}\right] .$](img607.gif) |
(434) |
Dies ist ebenfalls eine harmonische Schwingung der Kreisfrequenz 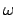 mit
der Amplitude
mit
der Amplitude 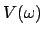 und der Phasenverschiebung
und der Phasenverschiebung 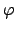 gegenüber der
anregenden Schwingung. Man sieht, daß vor allem zwei dimensionslose
Parameter in diese beiden Ausdrücke eingehen:
gegenüber der
anregenden Schwingung. Man sieht, daß vor allem zwei dimensionslose
Parameter in diese beiden Ausdrücke eingehen:
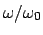 ,
das Verhältnis der anregenden Frequenz zur Eigenfrequenz
,
das Verhältnis der anregenden Frequenz zur Eigenfrequenz
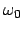 des ungestörten Systems und der Dämpfungsparameter
des ungestörten Systems und der Dämpfungsparameter
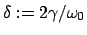 .
In Abb. 4.7(a) ist
.
In Abb. 4.7(a) ist
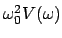 als Funktion dieser beiden
Parameter aufgezeichnet.
Man sieht, daß bei schwacher Dämpfung (kleine
als Funktion dieser beiden
Parameter aufgezeichnet.
Man sieht, daß bei schwacher Dämpfung (kleine 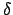 ) die Resonanz sehr
stark ausgeprägt ist.
) die Resonanz sehr
stark ausgeprägt ist. 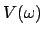 heißt deswegen auch der
Verzerrungsfaktor. Für zunehmende Dämpfung wird das Maximum der
Amplitude zu immer kleineren Frequenzen verschoben (genauso wie die
Frequenz der freien Schwingung, Gl. (4.22)). Bei sehr starker
Dämpfung, z.B.
heißt deswegen auch der
Verzerrungsfaktor. Für zunehmende Dämpfung wird das Maximum der
Amplitude zu immer kleineren Frequenzen verschoben (genauso wie die
Frequenz der freien Schwingung, Gl. (4.22)). Bei sehr starker
Dämpfung, z.B.
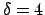 , gibt es kein Maximum mehr, die Amplitude der erzwungenen
Schwingung ist in weiten Bereichen unabhängig von der anregenden Frequenz,
aber sehr klein. Abb. 4.7(b) zeigt, daß für kleine
, gibt es kein Maximum mehr, die Amplitude der erzwungenen
Schwingung ist in weiten Bereichen unabhängig von der anregenden Frequenz,
aber sehr klein. Abb. 4.7(b) zeigt, daß für kleine
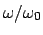 die
stationäre Schwingung in Phase mit der Erregung ist; bei
die
stationäre Schwingung in Phase mit der Erregung ist; bei
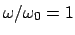 ist sie um 90^&cir#circ; verschoben, für noch höhere
ist sie um 90^&cir#circ; verschoben, für noch höhere
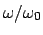 strebt die Phasendifferenz gegen 180^&cir#circ;.
strebt die Phasendifferenz gegen 180^&cir#circ;.
Abbildung:
Amplitude und Phasendiagramm eines gedämpften linearen Oszillators,
der von einer äußeren zeitharmonischen Kraft angeregt wird. Links gibt die
strichlierte Kurve die gedämpften Eigenschwingung an. Rechts gibt die ausgezogene
Kurve die erzwungene Schwingung, die strichlierte den Einschwingvorgang.
|
![\includegraphics[scale=0.8]{k4_phasend_ged_schw}](img616.gif) |
Abbildung 4.7:
(a) Resonanzkurven: Amplitude = Verzerrungsfaktor. (b) Resonanzkurven: Phase.
|
[]
![\includegraphics[scale=0.75]{k4_resonanzkurve_ampl}](img617.gif) []
[]
![\includegraphics[scale=0.75]{k4_resonanzkurve_phase}](img618.gif) |
Die Bewegung in einem Freiheitsgrad ist noch verhaltnismäßig übersichtlich.
Wenn die Kraft nur vom Ort abhängt, dann existiert sicher ein Potential,
die Energie ist erhalten, das System ist integrabel. Die Bewegung ist vorhersagbar.
Zwei Freiheitsgrade bieten wesentlich mehr Bewegungmöglichkeiten. Sind
die Bewegunggleichungen nichtlinear und gekoppelt, dann treten neue Phänomene auf,
insbesondere chaotische Bewegung. Zuerst wird aber der lineare Fall behandelt,
der isotrope und der anisotrope harmonische Oszillator. Diese Systeme
sind integrabel. Als ein Beispiel eines nichtlinearen, nicht integrablen Systems
wird das von Hénon-Heiles entwicklte Modell betrachtet.
Beim zweidimensionalen Oszillator muß man zwei Fälle unterscheiden, nämlich
ob die Kraft in allen Richtungen dieselbe ist (isotroper Oszillator,
Abb. 4.8(a)) oder in verschiedenen Richtungen verschieden
(anisotroper Oszillator, 4.8(b)) ist.
Abbildung 4.8:
(a) Der isotrope harmonische Oszillator.
(b) Der anisotrope Oszillator
|
[]
![\includegraphics[scale=0.7]{k4_iso_harm_oszi}](img619.gif) []
[]
![\includegraphics[scale=0.7]{k4_aniso_harm_oszi}](img620.gif) |
Beim isotropen Oszillator ist die Direktionskraft für alle Elongationen gleicher
Größe gleich groß und immer zum Gleichgewichtspunkt gerichtet. Dieser Punkt
wird als Koordinatenursprung genommen.
Die Kraft ist dann proportional zum Radiusvektor
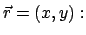
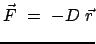 |
(435) |
Die Bewegungsgleichungen lauten:
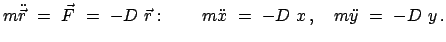 |
|
|
(436) |
mit der allgemeinen Lösung:
![$\displaystyle \vec r(t) = \left( \begin{array}{c} x(t) [2mm] y(t) \end{a...
... \varphi_{1}) [2mm] A_{2} \cos(\omega t + \varphi_{2}) \end{array} \right) .$](img625.gif) |
(437) |
Der Zusammenhang zwischen den beiden Darstellungen der allgemeinen Lösung
ist bereits bei Gln. (4.6) und (4.7) gegeben worden.
Eine spezielle Anfangsbedingung ist: 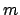 ist um die Strecke
ist um die Strecke 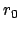 aus der
Ruhelage gezogen worden (Abb. 4.9(a)) :
aus der
Ruhelage gezogen worden (Abb. 4.9(a)) :
Abbildung:
Zwei Beispiele von Anfangsbedingungen für einen
zweidimensionalen harmonischen Oszillator und zugehörige Bahnen: (a) Radiale Elongation,
(b) Elongation und Stoß senkrecht dazu.
|
[]
![\includegraphics[scale=0.7]{k4_radial_elong_harm}](img627.gif) []
[]
![\includegraphics[scale=0.7]{k4_stosz_elong_harm}](img628.gif) |
Die zugehörige spezielle Lösung ist:
Dividiert man eine Lösung durch die andere, so findet man:
Der Massenpunkt oszilliert auf der Geraden
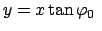 !
!
Eine andere Anfangsbedingung ist: 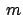 ist um die Länge
ist um die Länge 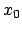 längs einer
Richtung aus der Ruhelage gezogen worden und erhält beim Auslassen einen
Stoß in der dazu senkrechten Richtung (Abb. 4.9(b)):
längs einer
Richtung aus der Ruhelage gezogen worden und erhält beim Auslassen einen
Stoß in der dazu senkrechten Richtung (Abb. 4.9(b)):
Die Konstanten bestimmt man wie zuvor und erhält die spezielle Lösung :
Die Bahnkurve ist eine Ellipse! Auch das vorherige Resultat stellt eine Ellipse
dar, wenn diese auch zu einer Strecke degeneriert ist. Unten wird gezeigt werden,
daß jede Bahnkurve eine Ellipse ist, deren Zentrum mit dem Kraftzentrum
zusammenfällt.
Mit der allgemeinen Lösung, Gl. (4.37), erhält man:
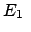 |
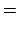 |
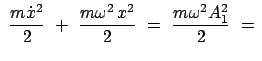 const. const.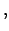 |
(438) |
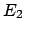 |
 |
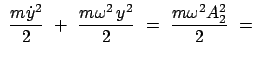 const. const.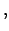 |
(439) |
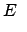 |
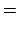 |
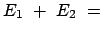 const. const. |
|
Die Gesamtenergie 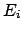 für die Bewegung in jeder Koordinatenrichtung ist erhalten,
damit auch die gesamte Energie
für die Bewegung in jeder Koordinatenrichtung ist erhalten,
damit auch die gesamte Energie 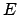 des Oszillators. Der Drehimpuls ist:
des Oszillators. Der Drehimpuls ist:
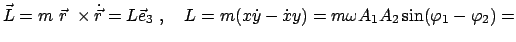 const. const. |
(440) |
Wann ist
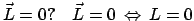 .
.
1) Wenn 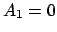 oder
oder 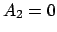 , d.h. wenn sich der Massenpunkt auf der
y-Achse oder x-Achse bewegt.
, d.h. wenn sich der Massenpunkt auf der
y-Achse oder x-Achse bewegt.
2) Wenn
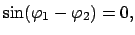 d.h.
d.h.
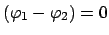 oder
oder 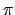 .
.
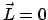 bedeutet eine Bewegung auf einer Geraden durch das Kraftzentrum.
bedeutet eine Bewegung auf einer Geraden durch das Kraftzentrum.
Ein weiteres Integral der Bewegung ist:
Die Zeitableitung von 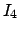 ist wegen der Bewegungsgleichungen (4.36)
Null. Wir haben also 4 Integrale der Bewegung,
ist wegen der Bewegungsgleichungen (4.36)
Null. Wir haben also 4 Integrale der Bewegung, 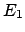 ,
, 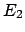 ,
, 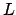 und
und 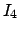 gefunden.
Die Gesamtenergie
gefunden.
Die Gesamtenergie
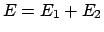 wird nicht mehr extra gezählt. Da das System nur
2 Freiheitsgrade hat, kann es nur 3 unabhängige zeitfreie Integrale der Bewegung
haben. Es muss also eine Beziehung zwischen den gerade angeführten Größen
bestehen. Diese ist unten angegeben. Man bestätigt sie durch Ausrechnen,
nachdem man die Definitionen aller vier Größen einsetzt hat.
wird nicht mehr extra gezählt. Da das System nur
2 Freiheitsgrade hat, kann es nur 3 unabhängige zeitfreie Integrale der Bewegung
haben. Es muss also eine Beziehung zwischen den gerade angeführten Größen
bestehen. Diese ist unten angegeben. Man bestätigt sie durch Ausrechnen,
nachdem man die Definitionen aller vier Größen einsetzt hat.
Im vierdimensionalen Phasenraum 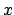 ,
, 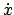 ,
, 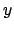 ,
, 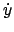 stellt jedes Integral
der Bewegung eine Hyperfläche, also einen dreidimensionalen Unterraum dar. Die
Phasenkurve muß auf jeder dieser Hyperflächen liegen. Der Durchschnitt zweier
derartiger dreidimensionaler Teilräume, z.B. der Hyperflächen, die
stellt jedes Integral
der Bewegung eine Hyperfläche, also einen dreidimensionalen Unterraum dar. Die
Phasenkurve muß auf jeder dieser Hyperflächen liegen. Der Durchschnitt zweier
derartiger dreidimensionaler Teilräume, z.B. der Hyperflächen, die 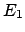 und
und
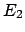 zugeordnet sind, ist ein zweidimensionaler Unterraum. Das dritte Integral
der Bewegung nimmt noch einen Freiheitsgrad weg. Es bleibt ein eindimensionaler
Unterraum übrig, das ist die Phasenkurve. Dies kann man hier auch ausrechnen.
Dazu werden im Quadrat des Drehimpulses die Quadrate der Geschwindigkeiten mittels
der Energiesätze
zugeordnet sind, ist ein zweidimensionaler Unterraum. Das dritte Integral
der Bewegung nimmt noch einen Freiheitsgrad weg. Es bleibt ein eindimensionaler
Unterraum übrig, das ist die Phasenkurve. Dies kann man hier auch ausrechnen.
Dazu werden im Quadrat des Drehimpulses die Quadrate der Geschwindigkeiten mittels
der Energiesätze 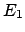 und
und 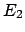 eliminiert. Die resultierende Gleichung wird
umgestellt und dann das Integral
eliminiert. Die resultierende Gleichung wird
umgestellt und dann das Integral 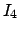 , Gl. (4.41), eingesetzt:
, Gl. (4.41), eingesetzt:
Der erste und der letzte Teil der letzten Zeile geben die Bahnkurve, einen
Kegelschnitt. Durch Hauptachsentransformation wird gezeigt, dass dieser eine
Ellipse darstellt. Hiezu wird diese Gleichung umgeschrieben:
Die Eigenwerte der Matrix M geben die Halbachsen des Kegelschnittes.
Diese sind beide positiv:
det
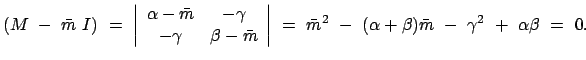
Die erste Zeile zeigt, dass der Radikand positiv ist. Die letzte Zeile zeigt,
dass die Wurzel kleiner ist als die vorhergehende Summe zweier positiver Grössen.
Daher sind beide Eigenwerte positiv; daher der Kegelschnitt eine Ellipse.
Eine zweite Methode zum Nachweis des gleichen Sachverhalts wird im nächsten Kapitel
entwickelt werden.
Der gerade rechnerisch gezeigte Zusammenhang läßt sich auch geometrisch
veranschaulichen. Da man den vollen vierdimensionalen Phasenraum nicht
anschaulich darstellen kann, muss man in einem dreidimensionalen Unterraum
arbeiten. Dieser wird geschaffen, indem die Geschwindigkeit 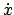 mittels des Energiesatzes
mittels des Energiesatzes 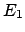 eliminiert wird. Im verbleibenden
Unterraum
eliminiert wird. Im verbleibenden
Unterraum
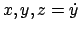 liefern das Quadrat des Drehimpulses
und der Energiesatz
liefern das Quadrat des Drehimpulses
und der Energiesatz 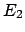 je eine (zweidimensionale) Fläche; deren
Durchschnitt gibt die Bahnkurve (s. Abb. 4.10).
je eine (zweidimensionale) Fläche; deren
Durchschnitt gibt die Bahnkurve (s. Abb. 4.10).
Der eben beschriebene Sachverhalt wird durch weitere Rechung ausgeführt.
Im Quadrat des Drehimpules, Gl. (4.40). werden 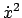 und
und 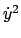 mittels der Energien
mittels der Energien 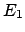 und
und 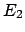 , Gln. (4.38)
und (4.39), eliminiert; ebenso
, Gln. (4.38)
und (4.39), eliminiert; ebenso 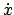 mittels des Drehimpulses,
Gl. (4.40).
mittels des Drehimpulses,
Gl. (4.40).
Im dreidimensionalen Unterraum
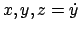 stellt dieses Polynom ein
einschaliges Hyperboloid dar. Auch dies wird wieder durch Hauptachsentransformation
der Matrix M gezeigt.
stellt dieses Polynom ein
einschaliges Hyperboloid dar. Auch dies wird wieder durch Hauptachsentransformation
der Matrix M gezeigt.
Daraus ergeben sich die Eigenwerte und Eigenvektoren :
Da zwei Eigenwerte positiv und einer negativ ist, ist die durch Gl. (4.42)
definierte Fläche ein einschaliges Hyperboloid; dessen Achse ist durch den Vektor
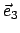 gegeben und liegt in der
gegeben und liegt in der
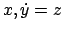 -Ebene.
-Ebene.
Zu Gl. (4.42) wird noch der Energiesatz 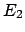 , Gl. (4.39),
hinzugenommen. Dieser stellt einen elliptischen Zylinder parallel zur
, Gl. (4.39),
hinzugenommen. Dieser stellt einen elliptischen Zylinder parallel zur
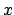 -Achse dar. Das Hyperboloid umschließt den Zylinder wie eine schief sitzende
Halskrause und berührt ihn längs einer Kurve, der Bahnkurve (s. Abb. 4.10).
-Achse dar. Das Hyperboloid umschließt den Zylinder wie eine schief sitzende
Halskrause und berührt ihn längs einer Kurve, der Bahnkurve (s. Abb. 4.10).
Abbildung:
Die Zylinderfläche entspricht 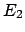 , Gl. (4.39);
das Hyperboloid, dessen Achse ebenfalls eingezeichnet ist, Gl. (4.42).
Die beiden Flächen berühren sich in der Bahnkurve.
, Gl. (4.39);
das Hyperboloid, dessen Achse ebenfalls eingezeichnet ist, Gl. (4.42).
Die beiden Flächen berühren sich in der Bahnkurve.
|
![\includegraphics[scale=0.82]{k4_zyl_hyperbol}](img701.gif) |
Wir nehmen nun an, daß die Federn in x-Richtung eine andere Direktionskraft
aufweisen als die in y-Richtung (s. Abb. 4.8(b)). Bei einer
Elongation der
Masse aus der Ruhlage ist die rücktreibende Kraft meist nicht mehr auf das
Kraftzentrum 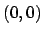 gerichtet. Die Bewegungsgleichungen lauten dann:
gerichtet. Die Bewegungsgleichungen lauten dann:
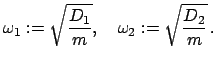 |
(444) |
Die allgemeine Lösung ist:
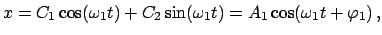 |
|
|
|
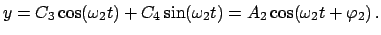 |
|
|
(445) |
Die Gesamtenergie ist:
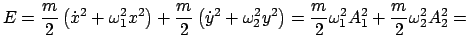 const. const. |
(446) |
Abbildung:
Entstehung einer Lissajous-Kurve mit Frequenzverhältnis 1:2.
|
|
Die zeitliche Änderung des Drehimpulses berechnet man direkt aus den
Bewegungsgleichungen:
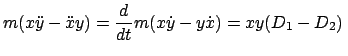 |
|
|
|
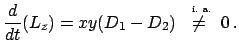 |
|
|
(447) |
Im allgemeinen ist der Drehimpuls nicht erhalten. Das hängt mit dem Fehlen
der radialen Symmetrie zusammen.
Es sind nun zwei Fälle möglich, je nachdem ob die Frequenzen kommensurabel
oder nicht kommensurabel sind.
Die Elimination der Zeit führt hier auf eine Kurvengleichung, die ein Polynom
in 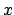 und
und 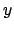 ist; die Bahn ist eine algebraische Kurve: Lissajous-Kurven.
Physikalisch: Es existiert ein kleinstes gemeinsames Vielfaches von
ist; die Bahn ist eine algebraische Kurve: Lissajous-Kurven.
Physikalisch: Es existiert ein kleinstes gemeinsames Vielfaches von 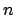 und
und
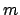 , d.h. nach einer gewissen Zeit befindet sich der Massenpunkt wieder am
Ausgangspunkt
, d.h. nach einer gewissen Zeit befindet sich der Massenpunkt wieder am
Ausgangspunkt
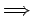 geschlossene Kurven, z.B. Abb. 4.11.
geschlossene Kurven, z.B. Abb. 4.11.
Die Frequenzen haben kein kleinstes gemeinsames Vielfaches, daher kehrt die
Kurve nicht an den Ausgangspunkt zurück. Sie erfüllt allmählich das ganze
umschriebene Rechteck mit den Seitenkanten
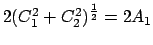 bzw.
bzw.
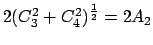 ,
(s. Abb. 4.12(b)). Man nennt diese Bewegung fastperiodisch oder
mehrfach periodisch (E.: almost periodic, multiply periodic).
Doch wird auch für ein Frequenzverhälnis,
das zwar rational, aber der Verhältnis zweier großer ganzer Zahlen ist, das
Periodenrechteck stark ausgefüllt (s. Abb. 4.12(a)).
Nun soll die Darstellung der Dynamik im Phasenraum behandelt werden.
Die Lagekoordinaten, Gl. (4.45), und die zugehörigen Impulse können
mit Relationen analog zu Gl. (4.14) folgendermaßen geschrieben werden.
,
(s. Abb. 4.12(b)). Man nennt diese Bewegung fastperiodisch oder
mehrfach periodisch (E.: almost periodic, multiply periodic).
Doch wird auch für ein Frequenzverhälnis,
das zwar rational, aber der Verhältnis zweier großer ganzer Zahlen ist, das
Periodenrechteck stark ausgefüllt (s. Abb. 4.12(a)).
Nun soll die Darstellung der Dynamik im Phasenraum behandelt werden.
Die Lagekoordinaten, Gl. (4.45), und die zugehörigen Impulse können
mit Relationen analog zu Gl. (4.14) folgendermaßen geschrieben werden.
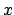 und
und 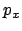 ,
, 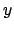 und
und 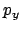 stellen in ihren jeweiligen zweidimensionalen
Phasenräumen Ellipsen dar, deren Halbachsen durch die Koeffizienten der
trigonometrischen Funktionen gegeben sind. Betrachtet man alle vier Variablen
stellen in ihren jeweiligen zweidimensionalen
Phasenräumen Ellipsen dar, deren Halbachsen durch die Koeffizienten der
trigonometrischen Funktionen gegeben sind. Betrachtet man alle vier Variablen
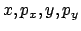 als Funktionen zweier unabhängiger Parameter
als Funktionen zweier unabhängiger Parameter 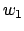 und
und 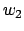 ,
dann stellen diese einen elliptischen Torus dar. Da aber
,
dann stellen diese einen elliptischen Torus dar. Da aber 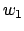 und
und 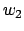 gemäß
den obigen Gleichungen Funktionen der Zeit
gemäß
den obigen Gleichungen Funktionen der Zeit 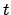 sind, liefern die obigen Funktionen
eine Raumkurve im vierdimensionalen Phasenraum, die Phasenkurve. Diese muß auf dem
Torus liegen. Ist das Frequenzverhältnis rational,
sind, liefern die obigen Funktionen
eine Raumkurve im vierdimensionalen Phasenraum, die Phasenkurve. Diese muß auf dem
Torus liegen. Ist das Frequenzverhältnis rational,
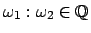 ,
dann bildet die Phasenkurve ein diskretes Netz auf dem Torus. Ist es irrational,
,
dann bildet die Phasenkurve ein diskretes Netz auf dem Torus. Ist es irrational,
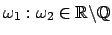 , dann überdeckt die Phasenkurve den
Torus im Laufe der Zeit vollständig.
, dann überdeckt die Phasenkurve den
Torus im Laufe der Zeit vollständig.
Die Poincaré-Abbildung ist ein wichtiges Hilfsmittel zur Untersuchung der
Existenz lokaler Integrale der Bewegung. Diese soll nun am Beispielen des
zweidimensionalen anisotropen harmonischen Oszillators erläutert werden.
Der Bewegung des Massenpunktes im zweidimensionalen Ortsraum entspricht im
vierdimensionale Phasenraum der Ablauf des Phasenpunkts auf der Phasenkurve.
Da man den vierdimensionalen Raum nicht darstellen kann, muß man sich mit
Projektionen begnügen.
Bei der Poincaré-Abbildung betrachtet man eine Ebene, einen zweidimensionalen
Unterraum des Phasenraumes, z.B. die 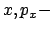 oder die
oder die 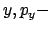 Ebene. In dieser
Ebene werden alle Punkte, an denen die Phasenbahn die Ebene durchstößt, eingetragen;
oder die Teilmenge der Durchstoßpunkte, die zu einer bestimmten
Geschwindigkeitsrichtung
gehören; also die zu
Ebene. In dieser
Ebene werden alle Punkte, an denen die Phasenbahn die Ebene durchstößt, eingetragen;
oder die Teilmenge der Durchstoßpunkte, die zu einer bestimmten
Geschwindigkeitsrichtung
gehören; also die zu 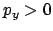 oder
oder 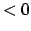 im ersten Fall,
also die zu
im ersten Fall,
also die zu 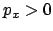 oder
oder 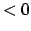 im zweiten Fall. Diese Konstruktion ist in
Abb. 4.13 für den zweidimensionalen harmonischen Oszillator dargestellt.
Bei kleinen Frequenzverhältnissen ist die Bewegung mit einem entsprechend kleinen
kleinsten gemeinsamen Vielfachen periodisch. Diese Zahl und damit die Zahl der
Druchstoßpunkte nehmen mit dem Frequenzverhältnis zu, sodaß eine quasikontinuierliche
Kurve entsteht. Im nächsten Pragraphen wird gezeigt, daß dies nur der Fall ist, wenn
entsprechend viele Integrale der Bewegung, zumindest lokal, existieren; andernfalls
füllen die Durchstoßpunkte die Ebene in einem weiten Bereich in unregelmäßiger und
chaotischer Weise.
im zweiten Fall. Diese Konstruktion ist in
Abb. 4.13 für den zweidimensionalen harmonischen Oszillator dargestellt.
Bei kleinen Frequenzverhältnissen ist die Bewegung mit einem entsprechend kleinen
kleinsten gemeinsamen Vielfachen periodisch. Diese Zahl und damit die Zahl der
Druchstoßpunkte nehmen mit dem Frequenzverhältnis zu, sodaß eine quasikontinuierliche
Kurve entsteht. Im nächsten Pragraphen wird gezeigt, daß dies nur der Fall ist, wenn
entsprechend viele Integrale der Bewegung, zumindest lokal, existieren; andernfalls
füllen die Durchstoßpunkte die Ebene in einem weiten Bereich in unregelmäßiger und
chaotischer Weise.
Ein System, das mathematisch einem nichtlinearen, gekoppelten Oszillator gleicht,
ist von Hénon und Heiles untersucht worden:
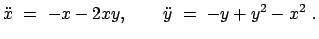 |
(450) |
Der erste Term jeder der rechten Seiten gibt eine lineare rücktreibende Kraft,
entspricht also einem linearen Oszillator mit der Masse 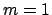 und der Kreisfrequenz
und der Kreisfrequenz
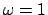 . Die weiteren Terme geben nichtlineare Koppelglieder.
. Die weiteren Terme geben nichtlineare Koppelglieder.
Das Modell zu den obigen Gleichungen stammt aber aus der Astronomie. Die beiden
Autoren untersuchten die Bewegung eines Sterns in dem sehr vereinfachten Modell
einer scheibenförmigen Galaxie. Die Kräfte entsprechen dem mittleren Kraftfeld,
das die übrigen Massen dieser Milchstraße erzeugen.
Man kann sofort das Potential und die Gesamtenergie angeben. (Dazu wird die erste
der obigen Gln. mit 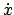 , die zweite mit
, die zweite mit 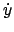 multipliziert; die resultierenden
Ausdrücke werden addiert.)
multipliziert; die resultierenden
Ausdrücke werden addiert.)
Das Potential 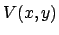 ist in Abb. 4.14(a) und
4.14(b) gezeigt. Es entspricht einer
ungefähr dreieckigen Potentialgrube, die an gewissen Teilen
des Randes von unendlich hohen Bergen begrenzt wird. Zwischen diesen Bergen gibt
es aber drei Pässe der Höhe
ist in Abb. 4.14(a) und
4.14(b) gezeigt. Es entspricht einer
ungefähr dreieckigen Potentialgrube, die an gewissen Teilen
des Randes von unendlich hohen Bergen begrenzt wird. Zwischen diesen Bergen gibt
es aber drei Pässe der Höhe
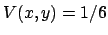 . Deren Sattelpunkte sind an den Stellen:
. Deren Sattelpunkte sind an den Stellen:
Der Wert 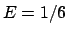 begrenzt den Bereich der stabilen Bewegung; für höhere Werte
der Gesamtenergie kann der Massenpunkt über einen der Pässe entkommen. Die Untersuchung
durch numerische Lösung der Bewegungsgleichungen zeigt, daß die Bewegung für
kleine Werte der Energie
begrenzt den Bereich der stabilen Bewegung; für höhere Werte
der Gesamtenergie kann der Massenpunkt über einen der Pässe entkommen. Die Untersuchung
durch numerische Lösung der Bewegungsgleichungen zeigt, daß die Bewegung für
kleine Werte der Energie 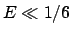 geordnet und voraussehbar ist. Aber selbst
für gebundene Zustände verläuft die Bewegung für eine Energie in der Nähe von,
jedoch unter
geordnet und voraussehbar ist. Aber selbst
für gebundene Zustände verläuft die Bewegung für eine Energie in der Nähe von,
jedoch unter 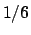 meist chaotisch und nicht voraussagbar.
meist chaotisch und nicht voraussagbar.
Zuerst ein Beispiel für niedrige Energie und hohe Ordnung: Bei Fehlen der nichtlinearen
Terme ist die Bahn eine Ellipse. Die nichtlinearen Terme bewirken, daß diese Ellipse
etwas verschoben und verdrückt wird; auch schließt sie sich nicht mehr
(Abb. 4.15(a)). Bei den in diesem Beispiel benützten
Anfangsbedingungen dreht sie sich ständig weiter,
(Abb. 4.15(b)), und füllt allmählich einen Teilbereich der 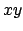 -Ebene aus,
(Abb. 4.15(c)). Die dreizählige Symmetrie des Potentials tritt dabei
klar zu Tage.
Diese Drehung führt zu einer periodischen Amplitudenmodulation der
-Ebene aus,
(Abb. 4.15(c)). Die dreizählige Symmetrie des Potentials tritt dabei
klar zu Tage.
Diese Drehung führt zu einer periodischen Amplitudenmodulation der 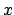 - und
- und 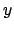 -
Koordinate des Massenpunkts, die eine regelmäßige Schwingung mit einer Periode
geringfügig größer als
-
Koordinate des Massenpunkts, die eine regelmäßige Schwingung mit einer Periode
geringfügig größer als 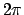 aufweisen, Abb. 4.16. Dies ist nur ein Beispiel,
das zu ganz speziellen
Anfangsbedingungen gehört. Andere Anfangsbedingungen können zu einer verdrückten
Bahnellipse führen, deren Achsen in einem begrenten Winkelbereich hin- und
herschwanken.
aufweisen, Abb. 4.16. Dies ist nur ein Beispiel,
das zu ganz speziellen
Anfangsbedingungen gehört. Andere Anfangsbedingungen können zu einer verdrückten
Bahnellipse führen, deren Achsen in einem begrenten Winkelbereich hin- und
herschwanken.
Abb. 4.17 zeigt eine chaotische Bahnkurve für einen Energiewert
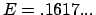 ,
der schon recht nahe am Grenzwert
,
der schon recht nahe am Grenzwert
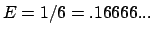 liegt. Die Bahnkurve ist
vollständig unregelmäßig; es ist unmöglich, aus dem bisherigen Verlauf derselben
irgendeine Voraussage über den zukünftigen zu machen, außer dieser, daß er
weiterhin chaotisch sein wird. Abbn. 4.18
geben die Koordinaten als Funktionen der Zeit. Man sieht unregelmäßige
Schwankungen der Periode und der Amplitude. Der Vergleich zwischen den ausgezogenen
und den strichlierten Kurven beweist, daß mit hoher Genauigkeit gerechnet werden
muß, wenn man für längere Zeiten verläßliche Resultate benötigt. Ein einfacher
Test ist, von der Endzeit zur Anfangszeit zurückzurechnen und nachzusehen, ob man
dabei wieder bei den Anfangsdaten ankommt; dabei muß man die Geschwindigkeiten
der Anfangsdaten für den Rücklauf umkehren. Doch auch für solche hohe Energiewerte
kann es spezielle Anfangswerte geben, für die man eine relativ regelmäßige und
übersichtliche Bahn erhält.
liegt. Die Bahnkurve ist
vollständig unregelmäßig; es ist unmöglich, aus dem bisherigen Verlauf derselben
irgendeine Voraussage über den zukünftigen zu machen, außer dieser, daß er
weiterhin chaotisch sein wird. Abbn. 4.18
geben die Koordinaten als Funktionen der Zeit. Man sieht unregelmäßige
Schwankungen der Periode und der Amplitude. Der Vergleich zwischen den ausgezogenen
und den strichlierten Kurven beweist, daß mit hoher Genauigkeit gerechnet werden
muß, wenn man für längere Zeiten verläßliche Resultate benötigt. Ein einfacher
Test ist, von der Endzeit zur Anfangszeit zurückzurechnen und nachzusehen, ob man
dabei wieder bei den Anfangsdaten ankommt; dabei muß man die Geschwindigkeiten
der Anfangsdaten für den Rücklauf umkehren. Doch auch für solche hohe Energiewerte
kann es spezielle Anfangswerte geben, für die man eine relativ regelmäßige und
übersichtliche Bahn erhält.
Abbildung 4.17:
Eine chaotische Bahn des Hénon-Heiles-Systems.
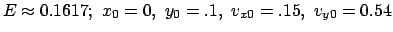 .
.
|
![\includegraphics[scale=0.86]{k4_hh_chaot_bahn}](img767.gif) |
Die wohlgeordnete Bewegung bei niedriger Energie gibt Anzeichen für das Wirken von
weiteren Integralen der Bewegung. Hiezu wird wieder die Poincaré-Abbildung
herangezogen. 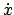 wird aus der Gleichung für die Gesamtenergie, Gl. (4.52),
berechnet. Es wird die Ebene
wird aus der Gleichung für die Gesamtenergie, Gl. (4.52),
berechnet. Es wird die Ebene 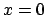 als die Ebene des Poincaré-Schnitts gewählt.
Es werden die Punkte in der
als die Ebene des Poincaré-Schnitts gewählt.
Es werden die Punkte in der 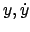 -Ebene gesucht, in denen die Phasenkurve
diese Ebene durchstößt. Diese werden in einem Bereich liegen, der durch die folgende
Bedingung festgelegt ist:
-Ebene gesucht, in denen die Phasenkurve
diese Ebene durchstößt. Diese werden in einem Bereich liegen, der durch die folgende
Bedingung festgelegt ist:
 |
(453) |
Abb. 4.19 zeigt die Poincaré-Schnitte für die beiden vorher behandelten
Beispiele. Der Schnitt zu niedriger Gesamtenergie führt zu geordneter Bewegung und
zu einer geschlossenen Kurve im Poincaré-Schnitt. Bei dem Energiewert, der knapp
unter der Bindungsenergie liegt, sind die Bewegung und damit auch die Verteilung der
Punkte im Poincaré-Schnitt chaotisch.
Variiert man bei geringer Energie, z.B. für 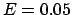 , die Anfangsbedingungen,
erhält man für jedes System von Anfangswerten eine geschlossene Kurve. Diese
Schar von Kurven scheint den ganzen Energiebereich, Gl. (4.53), auszufüllen.
Bei höheren Werten, z.B.
, die Anfangsbedingungen,
erhält man für jedes System von Anfangswerten eine geschlossene Kurve. Diese
Schar von Kurven scheint den ganzen Energiebereich, Gl. (4.53), auszufüllen.
Bei höheren Werten, z.B. 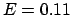 , ist ein neues Verhalten zu beobachten.
Für gewissen Anfangswerte gibt es eine ungeordnete, chaotische Menge von
Schnittpunkten, die alle zu einer Phasenkurve gehören. Phasenpunkte, die zu
anfänglich benachbarten Phasenkurven gehören, driften im Laufe der Zeit weit
auseinander. Für
, ist ein neues Verhalten zu beobachten.
Für gewissen Anfangswerte gibt es eine ungeordnete, chaotische Menge von
Schnittpunkten, die alle zu einer Phasenkurve gehören. Phasenpunkte, die zu
anfänglich benachbarten Phasenkurven gehören, driften im Laufe der Zeit weit
auseinander. Für 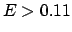 sind nur mehr ganz wenige Kurven vorhanden;
bei
sind nur mehr ganz wenige Kurven vorhanden;
bei
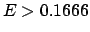 sind diese fast vollständig verschwunden.
sind diese fast vollständig verschwunden.
Solange geschlossene Kurven im Poincaré-Schnitt vorhanden sind, ist dies
als ein Hinweis auf die Wirksamkeit von zumindest lokal gültigen Integralen
der Bewegung aufzufassen.
Christian Sommer
2003-01-27
![]() , also
, also ![]() .
. ![]() wird nun in eine Taylorreihe um
wird nun in eine Taylorreihe um
![]() entwickelt:
entwickelt:
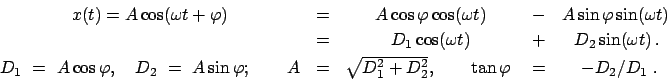
![]() ist aus der Ruhelage herausgezogen worden,
wird nun ausgelassen (Abb. 4.1).
ist aus der Ruhelage herausgezogen worden,
wird nun ausgelassen (Abb. 4.1).
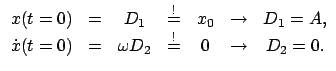
![\includegraphics[scale=0.93]{k4_schwingungsglg}](img497.gif)
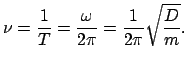
![]() die spezielle Lösung
die spezielle Lösung
![]() . Wenn der Massenpunkt anfänglich im
Gleichgewichtgspunkt in Ruhe ist, bleibt er es in alle Ewigkeit. - Wird die Masse
aus der Ruhelage gestoßen, gibt dies die Anfangsbedingungen:
. Wenn der Massenpunkt anfänglich im
Gleichgewichtgspunkt in Ruhe ist, bleibt er es in alle Ewigkeit. - Wird die Masse
aus der Ruhelage gestoßen, gibt dies die Anfangsbedingungen:
![]() Dies führt zur speziellen Lösung:
Dies führt zur speziellen Lösung:
![$\displaystyle 0 \quad \Rightarrow \quad
\frac{d}{dt} \left[ \frac{m}{2} \dot{x}^{2} + m \frac{\omega^{2}}{2} x^{2}
\right] = 0;$](img512.gif)
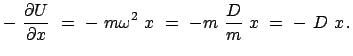
![]() eingezeichnet.
Für eine
gegebene Energie
eingezeichnet.
Für eine
gegebene Energie ![]() oszilliert der Massenpunkt zwischen den Punkten
oszilliert der Massenpunkt zwischen den Punkten ![]() und
und
![]() . Dies ergibt sich aus dem Energiesatz. Löst man
Gl. (4.13) nach der Geschwindigkeit
. Dies ergibt sich aus dem Energiesatz. Löst man
Gl. (4.13) nach der Geschwindigkeit ![]() auf, so ergibt sich:
auf, so ergibt sich:
![]() und
und
![]() )
hinzunimmt:
)
hinzunimmt:
![\includegraphics[scale=0.67]{k4_anharmschwing}](img530.gif)
![]() auf, findet man eine Differentialgleichung,
die durch Separation gelöst werden kann:
auf, findet man eine Differentialgleichung,
die durch Separation gelöst werden kann:
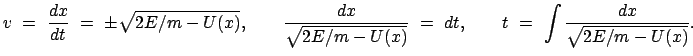
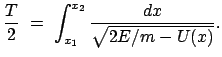
![]() (wie z.B. für
(wie z.B. für ![]() ) kann die Masse nach rechts bis ins
Unendliche laufen (
) kann die Masse nach rechts bis ins
Unendliche laufen (
![]() ) .
Ungebunder oder freier Zustand.
Im Bereich
) .
Ungebunder oder freier Zustand.
Im Bereich
![]() ist der Radikand ebenfalls positiv. Das Teilchen,
damit auch sein Phasenpunkt, können ins Unendliche gelangen (
ist der Radikand ebenfalls positiv. Das Teilchen,
damit auch sein Phasenpunkt, können ins Unendliche gelangen (![]() ).
Wenn der Massenpunkt einwärts läuft, dann wird er an der Stelle
).
Wenn der Massenpunkt einwärts läuft, dann wird er an der Stelle ![]() reflektiert und gelangt dann ins Uendliche. Doch ist dieser Bereich vom
physikalischen Standpunkt aus nicht sehr realistisch.
reflektiert und gelangt dann ins Uendliche. Doch ist dieser Bereich vom
physikalischen Standpunkt aus nicht sehr realistisch.
![]() an der Grenzenergie
an der Grenzenergie ![]() liegt, desto größer wird
der Wert der Periode. Denn bei
liegt, desto größer wird
der Wert der Periode. Denn bei
![]() fallen die Nullstellen
fallen die Nullstellen ![]() und
und
![]() zusammen,
zusammen,
![]() ; unter der Wurzel steht ein quadratischer
Ausdruck
; unter der Wurzel steht ein quadratischer
Ausdruck
![]() ;
der Integrand in dem obigen Ausdruck für die Periode hat einen Pol 1. Ordnung;
das Integral nimmt den Wert Unendlich an. Das Teilchen kann sich nur von links oder
rechts dem sog. Sattelpunkt nähern, es benötigt unendlich lange Zeit bis es
diesen erreicht ( --- ). Im Phasendiagramm entspricht dieser Bewegung die ausgezogene
Kurve; der Phasenpunkt kann aber immer nur einen Teil eines Astes dieser Kurve
durchlaufen.
Diese Bewegung heißt Limitationsbewegung. Diese Kurve trennt zwei Gebiete
des Phasenraumes, in denen verschiedenartige Bewegungen ablaufen. Deswegen heißt
sie auch Separatrix (E. separatrix).
;
der Integrand in dem obigen Ausdruck für die Periode hat einen Pol 1. Ordnung;
das Integral nimmt den Wert Unendlich an. Das Teilchen kann sich nur von links oder
rechts dem sog. Sattelpunkt nähern, es benötigt unendlich lange Zeit bis es
diesen erreicht ( --- ). Im Phasendiagramm entspricht dieser Bewegung die ausgezogene
Kurve; der Phasenpunkt kann aber immer nur einen Teil eines Astes dieser Kurve
durchlaufen.
Diese Bewegung heißt Limitationsbewegung. Diese Kurve trennt zwei Gebiete
des Phasenraumes, in denen verschiedenartige Bewegungen ablaufen. Deswegen heißt
sie auch Separatrix (E. separatrix).
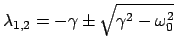
![]() eine gedämpfte Schwingung (E.: damped oscillation).
Für
eine gedämpfte Schwingung (E.: damped oscillation).
Für
![]() kommt der Oszillator wegen der Reibungsverluste zur Ruhe.
Als Beispiel ist der Fall mit
kommt der Oszillator wegen der Reibungsverluste zur Ruhe.
Als Beispiel ist der Fall mit ![]() in Abb. 4.3 gezeigt.
in Abb. 4.3 gezeigt.
![\includegraphics[scale=0.83]{k4_gedaempfteschw}](img567.gif)
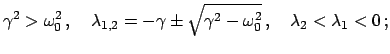
![]() wirkt neben den Federn (oder sonstigen elastischen
Kräften, die ihn in die Ruhelage zurückziehen wollen,
noch eine zusätzliche zeitabhängige Kraft
wirkt neben den Federn (oder sonstigen elastischen
Kräften, die ihn in die Ruhelage zurückziehen wollen,
noch eine zusätzliche zeitabhängige Kraft
![]() :
:
![]() hängt von der Form der Kraft
hängt von der Form der Kraft ![]() ab.
Besonders wichtig sind periodische Anregungen. Wir betrachten den Sonderfall
einer harmonischen Störkraft der Kreisfrequenz
ab.
Besonders wichtig sind periodische Anregungen. Wir betrachten den Sonderfall
einer harmonischen Störkraft der Kreisfrequenz ![]() .
.
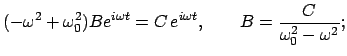
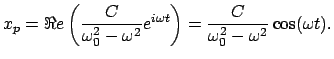
![\includegraphics[scale=0.8]{k4_elong_imp_phasend}](img591.gif)
![]() und
und
![]() .
.
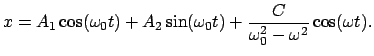
![]() (Resonanz, E.: resonance).
In diesem Fall ist die Reibung so wesentlich, daß sie nicht vernachlässigt
werden darf. Wir betrachten daher die Gleichung
(Resonanz, E.: resonance).
In diesem Fall ist die Reibung so wesentlich, daß sie nicht vernachlässigt
werden darf. Wir betrachten daher die Gleichung
![]() 4.1.3),
4.1.3),
![]() . Wieder erhalten wir eine partikuläre Lösung
der obigen inhomogenen Gleichung durch den Ansatz
. Wieder erhalten wir eine partikuläre Lösung
der obigen inhomogenen Gleichung durch den Ansatz
![]() :
:
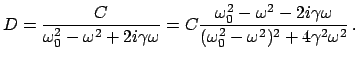
![]() , der partikulären
Lösung von (4.30), und aus der allg. Lösung (4.22)
der homogenen Gleichung (4.19):
, der partikulären
Lösung von (4.30), und aus der allg. Lösung (4.22)
der homogenen Gleichung (4.19):
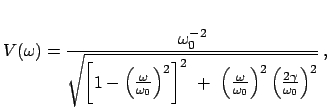
![$\displaystyle \varphi = \arctan \frac{\omega_{0}^{2} - \omega^{2}}{2 \omega \ga...
...mega_{0}^2}}{\frac{\omega}{\omega_{0}} \frac{2 \gamma}{\omega_{0}}}\right] .$](img607.gif)
![\includegraphics[scale=0.8]{k4_phasend_ged_schw}](img616.gif)
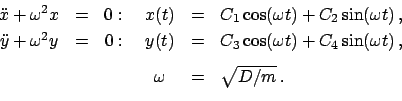
![\includegraphics[scale=0.7]{k4_radial_elong_harm}](img627.gif) []
[]
![\includegraphics[scale=0.7]{k4_stosz_elong_harm}](img628.gif)
![$\displaystyle t = 0: \quad
\vec {r}(t=0) = \left( \begin{array}{c} r_{0} \c...
...{\vec r}(t=0) = \left( \begin{array}{c} 0 [2mm] 0 \end{array} \right);
$](img629.gif)
![$\displaystyle \vec r(t=0) = \left( \begin{array}{c} C_1 [2mm] C_3 \end{a...
...)
\stackrel{!}{=} \left( \begin{array}{c} 0 [2mm] 0 \end{array} \right);$](img630.gif)
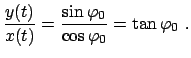
![]() ist um die Länge
ist um die Länge ![]() längs einer
Richtung aus der Ruhelage gezogen worden und erhält beim Auslassen einen
Stoß in der dazu senkrechten Richtung (Abb. 4.9(b)):
längs einer
Richtung aus der Ruhelage gezogen worden und erhält beim Auslassen einen
Stoß in der dazu senkrechten Richtung (Abb. 4.9(b)):
![$\displaystyle t = 0: \quad
\vec r(t=0) = \left( \begin{array}{c} x_0 [2...
...c r}(t=0) = \left( \begin{array}{c} 0 [2mm] v_0 \end{array} \right) .
$](img636.gif)
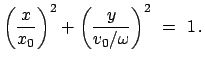
![]() ,
, ![]() ,
, ![]() ,
, ![]() stellt jedes Integral
der Bewegung eine Hyperfläche, also einen dreidimensionalen Unterraum dar. Die
Phasenkurve muß auf jeder dieser Hyperflächen liegen. Der Durchschnitt zweier
derartiger dreidimensionaler Teilräume, z.B. der Hyperflächen, die
stellt jedes Integral
der Bewegung eine Hyperfläche, also einen dreidimensionalen Unterraum dar. Die
Phasenkurve muß auf jeder dieser Hyperflächen liegen. Der Durchschnitt zweier
derartiger dreidimensionaler Teilräume, z.B. der Hyperflächen, die ![]() und
und
![]() zugeordnet sind, ist ein zweidimensionaler Unterraum. Das dritte Integral
der Bewegung nimmt noch einen Freiheitsgrad weg. Es bleibt ein eindimensionaler
Unterraum übrig, das ist die Phasenkurve. Dies kann man hier auch ausrechnen.
Dazu werden im Quadrat des Drehimpulses die Quadrate der Geschwindigkeiten mittels
der Energiesätze
zugeordnet sind, ist ein zweidimensionaler Unterraum. Das dritte Integral
der Bewegung nimmt noch einen Freiheitsgrad weg. Es bleibt ein eindimensionaler
Unterraum übrig, das ist die Phasenkurve. Dies kann man hier auch ausrechnen.
Dazu werden im Quadrat des Drehimpulses die Quadrate der Geschwindigkeiten mittels
der Energiesätze ![]() und
und ![]() eliminiert. Die resultierende Gleichung wird
umgestellt und dann das Integral
eliminiert. Die resultierende Gleichung wird
umgestellt und dann das Integral ![]() , Gl. (4.41), eingesetzt:
, Gl. (4.41), eingesetzt:
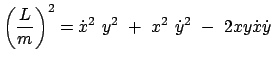
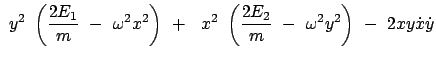
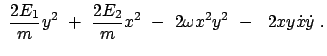
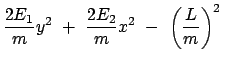
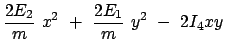
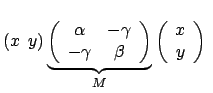
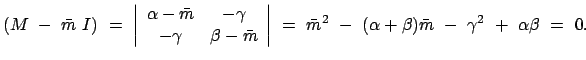
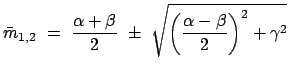
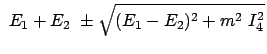
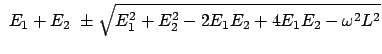
![]() mittels des Energiesatzes
mittels des Energiesatzes ![]() eliminiert wird. Im verbleibenden
Unterraum
eliminiert wird. Im verbleibenden
Unterraum
![]() liefern das Quadrat des Drehimpulses
und der Energiesatz
liefern das Quadrat des Drehimpulses
und der Energiesatz ![]() je eine (zweidimensionale) Fläche; deren
Durchschnitt gibt die Bahnkurve (s. Abb. 4.10).
je eine (zweidimensionale) Fläche; deren
Durchschnitt gibt die Bahnkurve (s. Abb. 4.10).
![]() und
und ![]() mittels der Energien
mittels der Energien ![]() und
und ![]() , Gln. (4.38)
und (4.39), eliminiert; ebenso
, Gln. (4.38)
und (4.39), eliminiert; ebenso ![]() mittels des Drehimpulses,
Gl. (4.40).
mittels des Drehimpulses,
Gl. (4.40).

![]() , Gl. (4.39),
hinzugenommen. Dieser stellt einen elliptischen Zylinder parallel zur
, Gl. (4.39),
hinzugenommen. Dieser stellt einen elliptischen Zylinder parallel zur
![]() -Achse dar. Das Hyperboloid umschließt den Zylinder wie eine schief sitzende
Halskrause und berührt ihn längs einer Kurve, der Bahnkurve (s. Abb. 4.10).
-Achse dar. Das Hyperboloid umschließt den Zylinder wie eine schief sitzende
Halskrause und berührt ihn längs einer Kurve, der Bahnkurve (s. Abb. 4.10).
![\includegraphics[scale=0.82]{k4_zyl_hyperbol}](img701.gif)
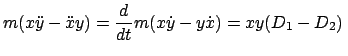
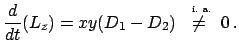
![\includegraphics[scale=0.74]{k4_period_bew}](img722.gif)
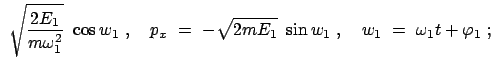
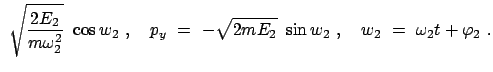
![]() oder die
oder die ![]() Ebene. In dieser
Ebene werden alle Punkte, an denen die Phasenbahn die Ebene durchstößt, eingetragen;
oder die Teilmenge der Durchstoßpunkte, die zu einer bestimmten
Geschwindigkeitsrichtung
gehören; also die zu
Ebene. In dieser
Ebene werden alle Punkte, an denen die Phasenbahn die Ebene durchstößt, eingetragen;
oder die Teilmenge der Durchstoßpunkte, die zu einer bestimmten
Geschwindigkeitsrichtung
gehören; also die zu ![]() oder
oder ![]() im ersten Fall,
also die zu
im ersten Fall,
also die zu ![]() oder
oder ![]() im zweiten Fall. Diese Konstruktion ist in
Abb. 4.13 für den zweidimensionalen harmonischen Oszillator dargestellt.
Bei kleinen Frequenzverhältnissen ist die Bewegung mit einem entsprechend kleinen
kleinsten gemeinsamen Vielfachen periodisch. Diese Zahl und damit die Zahl der
Druchstoßpunkte nehmen mit dem Frequenzverhältnis zu, sodaß eine quasikontinuierliche
Kurve entsteht. Im nächsten Pragraphen wird gezeigt, daß dies nur der Fall ist, wenn
entsprechend viele Integrale der Bewegung, zumindest lokal, existieren; andernfalls
füllen die Durchstoßpunkte die Ebene in einem weiten Bereich in unregelmäßiger und
chaotischer Weise.
im zweiten Fall. Diese Konstruktion ist in
Abb. 4.13 für den zweidimensionalen harmonischen Oszillator dargestellt.
Bei kleinen Frequenzverhältnissen ist die Bewegung mit einem entsprechend kleinen
kleinsten gemeinsamen Vielfachen periodisch. Diese Zahl und damit die Zahl der
Druchstoßpunkte nehmen mit dem Frequenzverhältnis zu, sodaß eine quasikontinuierliche
Kurve entsteht. Im nächsten Pragraphen wird gezeigt, daß dies nur der Fall ist, wenn
entsprechend viele Integrale der Bewegung, zumindest lokal, existieren; andernfalls
füllen die Durchstoßpunkte die Ebene in einem weiten Bereich in unregelmäßiger und
chaotischer Weise.
![]() , die zweite mit
, die zweite mit ![]() multipliziert; die resultierenden
Ausdrücke werden addiert.)
multipliziert; die resultierenden
Ausdrücke werden addiert.)
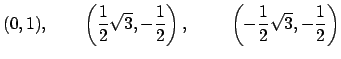
![\includegraphics[scale=0.73]{k4_hh_pot_relief}](img754.gif) []
[]
![\includegraphics[scale=0.65]{k4_hh_pot_contur}](img755.gif)
![]() begrenzt den Bereich der stabilen Bewegung; für höhere Werte
der Gesamtenergie kann der Massenpunkt über einen der Pässe entkommen. Die Untersuchung
durch numerische Lösung der Bewegungsgleichungen zeigt, daß die Bewegung für
kleine Werte der Energie
begrenzt den Bereich der stabilen Bewegung; für höhere Werte
der Gesamtenergie kann der Massenpunkt über einen der Pässe entkommen. Die Untersuchung
durch numerische Lösung der Bewegungsgleichungen zeigt, daß die Bewegung für
kleine Werte der Energie ![]() geordnet und voraussehbar ist. Aber selbst
für gebundene Zustände verläuft die Bewegung für eine Energie in der Nähe von,
jedoch unter
geordnet und voraussehbar ist. Aber selbst
für gebundene Zustände verläuft die Bewegung für eine Energie in der Nähe von,
jedoch unter ![]() meist chaotisch und nicht voraussagbar.
meist chaotisch und nicht voraussagbar.
![\includegraphics[scale=0.8]{k4_hh_sys_bahn_1p}](img759.gif) []
[]
![\includegraphics[scale=0.8]{k4_hh_sys_bahn_4p}](img760.gif) []
[]
![\includegraphics[scale=0.8]{k4_hh_sys_bahn_125p}](img761.gif)
![]() ,
der schon recht nahe am Grenzwert
,
der schon recht nahe am Grenzwert
![]() liegt. Die Bahnkurve ist
vollständig unregelmäßig; es ist unmöglich, aus dem bisherigen Verlauf derselben
irgendeine Voraussage über den zukünftigen zu machen, außer dieser, daß er
weiterhin chaotisch sein wird. Abbn. 4.18
geben die Koordinaten als Funktionen der Zeit. Man sieht unregelmäßige
Schwankungen der Periode und der Amplitude. Der Vergleich zwischen den ausgezogenen
und den strichlierten Kurven beweist, daß mit hoher Genauigkeit gerechnet werden
muß, wenn man für längere Zeiten verläßliche Resultate benötigt. Ein einfacher
Test ist, von der Endzeit zur Anfangszeit zurückzurechnen und nachzusehen, ob man
dabei wieder bei den Anfangsdaten ankommt; dabei muß man die Geschwindigkeiten
der Anfangsdaten für den Rücklauf umkehren. Doch auch für solche hohe Energiewerte
kann es spezielle Anfangswerte geben, für die man eine relativ regelmäßige und
übersichtliche Bahn erhält.
liegt. Die Bahnkurve ist
vollständig unregelmäßig; es ist unmöglich, aus dem bisherigen Verlauf derselben
irgendeine Voraussage über den zukünftigen zu machen, außer dieser, daß er
weiterhin chaotisch sein wird. Abbn. 4.18
geben die Koordinaten als Funktionen der Zeit. Man sieht unregelmäßige
Schwankungen der Periode und der Amplitude. Der Vergleich zwischen den ausgezogenen
und den strichlierten Kurven beweist, daß mit hoher Genauigkeit gerechnet werden
muß, wenn man für längere Zeiten verläßliche Resultate benötigt. Ein einfacher
Test ist, von der Endzeit zur Anfangszeit zurückzurechnen und nachzusehen, ob man
dabei wieder bei den Anfangsdaten ankommt; dabei muß man die Geschwindigkeiten
der Anfangsdaten für den Rücklauf umkehren. Doch auch für solche hohe Energiewerte
kann es spezielle Anfangswerte geben, für die man eine relativ regelmäßige und
übersichtliche Bahn erhält.
![]() wird aus der Gleichung für die Gesamtenergie, Gl. (4.52),
berechnet. Es wird die Ebene
wird aus der Gleichung für die Gesamtenergie, Gl. (4.52),
berechnet. Es wird die Ebene ![]() als die Ebene des Poincaré-Schnitts gewählt.
Es werden die Punkte in der
als die Ebene des Poincaré-Schnitts gewählt.
Es werden die Punkte in der ![]() -Ebene gesucht, in denen die Phasenkurve
diese Ebene durchstößt. Diese werden in einem Bereich liegen, der durch die folgende
Bedingung festgelegt ist:
-Ebene gesucht, in denen die Phasenkurve
diese Ebene durchstößt. Diese werden in einem Bereich liegen, der durch die folgende
Bedingung festgelegt ist:
![\includegraphics[scale=0.78]{k4_poincare_geord_bew}](img776.gif) []
[]
![\includegraphics[scale=0.75]{k4_poincare_ungeord_bew}](img777.gif)