Next: Quantified MaxEnt Up: Abel Inversion using the Previous: Introduction Contents
For numeric calculations we approximate the density ![]() by a piecewise
constant function:
by a piecewise
constant function:
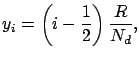 |
(4) |
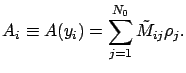 |
(5) |
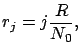 |
(6) |
In order to ensure smoothness of the plasma density ![]() we represent it
by a natural cubic spline passing through
we represent it
by a natural cubic spline passing through ![]() control points
control points
![]() and calculate
and calculate ![]() by interpolation at
by interpolation at ![]() . Fixing
. Fixing
![]() and
and ![]() while varying only
while varying only
![]() , we get
, we get ![]() by a simple matrix multiplication:
by a simple matrix multiplication:
![]() . In
order to obtain the spline matrix
. In
order to obtain the spline matrix ![]() we calculate the cubic spline
we calculate the cubic spline
![]() passing through
passing through
![]() and set
and set
![]() .
.
We finally arrive at a matrix equation relating
![]() and the
absorbance
and the
absorbance ![]() :
: