Taking into account noise 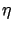 which is always present in expermental data,
we have to rewrite (8) as
which is always present in expermental data,
we have to rewrite (8) as
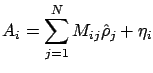 |
(9) |
In order to infer
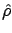 , we apply
Bayesian probability theory for the calculation of the posterior probability
, we apply
Bayesian probability theory for the calculation of the posterior probability
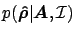 of a density distribution
of a density distribution
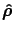 given the absorbance data
given the absorbance data
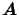 . Using Bayes' Theorem we obtain:
. Using Bayes' Theorem we obtain:
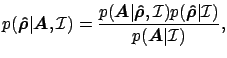 |
(10) |
Assuming uncorrelated Gaussian noise with mean zero and variance
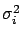 the likelihood is given by:
the likelihood is given by:
![$\displaystyle p({\boldsymbol{A}}\vert{\boldsymbol{\hat{\rho}}},\mathcal{I}) = \...
...N_d} \left[\frac{A_i - \sum_j M_{ij} \hat{\rho}_j }{\sigma_i} \right]^2 \right)$](img41.gif) |
(11) |
As prior we choose the MaxEnt prior (see e.g. [Siv96] for
further discussion):
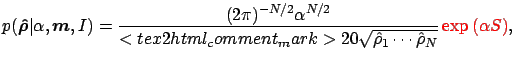 |
(12) |
with hyperparameter 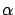 , default model
, default model
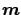 and entropy
and entropy 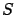 defined by:
defined by:
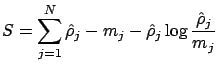 |
(13) |
The default model
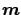 is the MaxEnt-solution in case of strong
regularization
is the MaxEnt-solution in case of strong
regularization
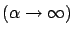 .
.
In order to obtain the maximum posterior or MAP solution for fixed
hyperparameter 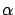 , we have to maximize
, we have to maximize
denoting the misfit by
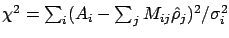 and ignoring the denominator in
(12) since we assume that it does not vary much compared
to the exponential. The maximum is calculated numerically by Newton's method,
for the details we refer to [Lin01].
and ignoring the denominator in
(12) since we assume that it does not vary much compared
to the exponential. The maximum is calculated numerically by Newton's method,
for the details we refer to [Lin01].
Finally we have to specify the optimal hyperparameter 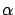 , which is fixed
by the relation:
, which is fixed
by the relation:
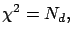 |
(14) |
since we expect each data point 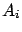 to deviate by
to deviate by 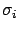 from its true
value on average. Starting with large
from its true
value on average. Starting with large 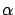 (in order to ensure
convergence of the Newton iterations), the hyperparameter is determined by
interval bisection.
(in order to ensure
convergence of the Newton iterations), the hyperparameter is determined by
interval bisection.
Danilo Neuber
2003-10-03
![]() which is always present in expermental data,
we have to rewrite (8) as
which is always present in expermental data,
we have to rewrite (8) as
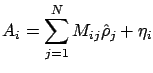
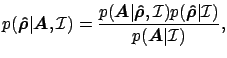
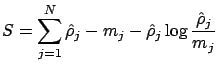
![]() , we have to maximize
, we have to maximize
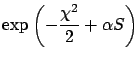
![]() , which is fixed
by the relation:
, which is fixed
by the relation: