Das Einheitsquaternion
BITTE LÖSCHEN
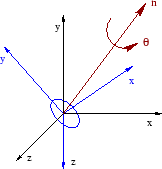
Das Quaternion beschreibt eine Rotation um einen Vektor, der durch den Ursprung des Koordinatensystems geht. In der Abbildung sind ein Einheitsvektor [math]\mathbf{n}[/math] und ein Winkel [math]\theta[/math] dargestellt, die die Rotation der beiden Koordinatensysteme beschreiben. Das blaue Koordinatensystem ist das Ergebnis der Drehung des schwarzen Systems um einen Winkel [math]\theta[/math].
Das Quaternion geht auf Hamilton zurueck und kann mathematisch als eine komplexe Zahl mit drei verschiedenen imaginaeren Anteilen behandelt werden:
[math]\dot q = q_0 + \mathfrak{i}q_x + \mathfrak{j}q_y + \mathfrak{k}q_z[/math] mit [math]\ q_0, q_x, q_y, q_z \in \mathbb{R}.[/math]
Bei gegebenem Einheitsvektor [math]\mathbf{n}= (n_x, n_y, n_z)^T[/math] und Rotationswinkel [math]\theta_n[/math] laesst sich das Einheitsquaternion berechnen durch:
[math]q_0 = \cos \frac{\theta_n}{2}[/math]
[math]q_x = n_x \, \sin \frac{\theta_n}{2}[/math]
[math]q_y = n_y \, \sin \frac{\theta_n}{2}[/math]
[math]q_z = n_z \, \sin \frac{\theta_n}{2}.[/math]
Die Rotationsmatrix berechnet sich aus einem Einheitsquaternion [math]\dot q [/math] wie folgt:
[math]R = \begin{pmatrix} (q_0^2 + q_x^2 - q_y^2 - q_z^2) & 2(q_xq_y + q_zq_0) & 2(q_xq_z + q_yq_0) \\ 2(q_xq_y + q_zq_0) & (q_0^2 - q_x^2 + q_y^2 + q_z^2) & 2(q_yq_z - q_xq_0) \\
2(q_zq_x - q_yq_0) & 2(q_zq_y + q_xq_0) & (q_0^2 - q_x^2 - q_y^2 + q_z^2) \end{pmatrix}[/math]
Die Verwendung des Einheitsquaternions zur Darstellung von Rotationen garantiert, dass die entsprechende Rotationsmatrix orthonormal ist.