MLTutor - Hints

Einführung

Assignment

Für die Zuweisung von Werten zu einer Variablen wird das Zeichen = verwendet:

a = 3;
b = 7.5; % Der Punkt steht für Komma
c = 1.7e-5; % 1.7 * 10^(-5)
d = pi; % Die Zahl Pi ist bekannt

Variablen werden überschrieben, daher hat nach

a = 1;
a = 2;
a = 3;

die Variable a den Wert 3 und jeglicher Bezug zu den vorherigen Werten ist verloren.

Einfache Rechnungen

Einfache Rechnungen mit arithmetischen Operatoren funktionieren so

x1 = 3 + 4;
x2 = x1 * 2;

wäre identisch mit

x2 = (3 + 4) * 2;

Die runden Klammern dienen hier der Gliederung. Wie bei normalen Rechnungen ist die Reihenfolge der Abarbeitung

Potenzieren

Multiplizieren, Dividieren

Addieren, Subtrahieren

Daher liefert

x3 = 3 + 4 * 2

etwas anderes als x2 von oben.

Ansonsten erfolgt die Abarbeitung von Links nach Rechts

2 / 2 / 2 

liefert als Ergebnis 0.5, wohingegen

2 / (2 / 2)

das Ergebnis 2 liefern würde.

Bei folgenden Typen von Aufgaben sollte man ganz Besonders an die Reihenfolge der Abarbeitung denken:

(a + b) / (a - b)
(a + b) / a - b % Gleich wie ((a + b) / a) - b
a + b / a - b % Gleich wie a + (b / a) - b
a^(3 / 2)
a^3 / 2 % Das Ergebnis von a^3 wird durch 2 dividiert
(a + b)^2 
a + b^2 % Nur b wird quadriert

Einfache Funktionen

Funktionen können in folgender Form aufgerufen werden

x1 = sin(1.5);
x2 = cos(pi/2); Cosinus von pi/2
x3 = cos(pi/4) / 2; Cosinus von pi/4, dann das Ergebnis durch 2 dividiert
x4 = 5 + tan(3);
a = pi/4;
b = sin(a)^2 % Sinus von a, dann das Ergebnis quadriert

Doppelpunkt

Mit der Doppelpunkt-Notation (colon) kann man sehr einfach Zeilenvektoren erstellen. Der Befehl

x = 1:5;

erzeugt den Vektor

1 2 3 4 5

Folgende Befehle erzeugen die dargestellten Ergebnisse:

x = 0:4;    % 0 1 2 3 4
x = 0:2:4;  % 0 2 4
x = 0:2:5;  % 0 2 4
x = 0:5:5;  % 0 5
x = 1:5:5;  % 1
x = 5:0;    % [] entspricht einem leeren Feld
x = 5:-1:0; % 5 4 3 2 1 0

Die Syntax ist also

start:schritt:ende

oder

start:ende

wobei hier die Standard-Schrittweite 1 verwendet wird.

linspace

Mit dem Matlab Befehl linspace kann man Vektoren von einem Startwert bis zu einem Endwert mit äquidistantem Abstand erzeugen

x = linspace(0,1,11); % 0.0 0.1 0.2 ... 1.0

wobei Anfangs und Endpunkt immer Teil des Vektor sind.

x = linspace(anfang,ende,num) % num ist die Länge des Vektors
x = linspace(anfang,ende) % Der Defaultwert für num = 100

input

Will man vom Benutzer eines Skripts Werte abfragen, sollte man die Matlab Funktion input verwenden:

var = input('Bitte geben Sie der Variablen var einen Wert: ');
x = var^2;
...

Dann sieht man

Bitte geben Sie der Variablen var einen Wert: |

Man kann nun einen Wert angeben und die Zeile mit <ENTER> beenden

Bitte geben Sie der Variablen var einen Wert: 3.75 <ENTER-TASTE>

und danach hat die Variable var den Wert 3.75 und die Berechnungen laufen weiter ab.

Defaultwerte bei input

Wird vom Benutzer kein Wert eingegeben und lediglich die <ENTER-TASTE> betätigt wird die Variable mit einem leeren Feld belegt. Deshalb ist es möglich mit Hilfe von isempty einen Defaultwert zu vergeben.

var = input('Bitte geben Sie der Variablen var einen Wert: ');
if isempty(var), var = 5; end

Workspace

clear

Mit dem Befehl clear können lokale und globale Variablen im Matlab-Wokspace gelöscht werden. Bei allen Übungsabgaben soll das nicht gemacht werden. In MLTutor-Tests ist der Befehl clear lahm gelegt und mit der Variablen MLTutor_CLEAR_COUNT kann gezählt werden, wie oft clear verwendet wird.

Formatierung

Strichpunkt

Matlab Skripts und Funktionen sollten so geschrieben werden, dass sie keine Ausgabe am Schirm machen, die nicht explizit durch disp oder fprintf im Program veranlasst wird. Daher muss man am Ende von Anweisungen, die eine Ausgabe erzeugen einen Strichpunkt verwenden.

Korrekt:

x = 1:5; 
y = x.^2;
plot(x,y)

Ebenfalls korrekt sind Befehle in einer Zeile:

x = 1:5; y = x.^2; plot(x,y)

Ebenfalls korrekt, da jetzt auch Ausgabe vom Befehl plot:

x = 1:5; y = x.^2; ph=plot(x,y);

Syntax korrekt, erzeugt aber unerwünschte Ausgabe:

x = 1:5
y = x.^2
plot(x,y)

Syntax korrekt, erzeugt aber unerwünschte Ausgabe, da Beistrich satt Strichpunkt als Trennzeichen verwendet wird:

x = 1:5, y = x.^2, plot(x,y)

Syntax nicht korrekt, da Befehle in einer Zeile nicht einfach aneinander gereiht werden können:

x = 1:5 y = x.^2 plot(x,y)

In MLTutor Tests können fehlende Strichpunkte an Hand der Variablen MLTutor_DISPLAY_COUNT überprüft werden. Ist dieser Wert nicht Null fehlen Strichpunkte. Alle Übungsabgaben sollen so geschrieben sein, dass sie keine fehlenden Strichpunkte enthalten.

Kommentare

Kommentare kann man in Matlab schreiben, wenn man das Zeichen % verwendet. Das kann am Anfang der Zeile oder aber nach Befehlen gemacht werden:

% Initialisieren von Werten
x_start = 0; % Startwert
x_end = pi; % Endwert

Kommentare sollen sinnvoll zur Dokumentation von Programmen eingesetzt werden.

Hilfe

Der erste zusammenhängende Block von Kommentarzeilen in einem Skript oder einer Funktion wird bei Verwendung des Befehls help am Schirm ausgegeben. Dieser Text soll über den Aufruf bzw. die Aufgaben eines Matlab-Skrips oder einer Matlab-Funktion Auskunft geben:

function h = secansh(x,x_0,s)
% Funktion: secansh
% Aufruf: h = secansh(x,x_0,s)
% Berechnet fuer den Vektor x die Werte der normierten Secans Hyperbolicus 
% Funktion mit dem Maximum bei x_0 und mit der Halbwertsbreite s
% Input:  Vektor x, Skalar x_0, Skalar s
% Output: Vektor h(x)
%
% Name: Winfried Kernbichler
% Datum: 15.02.2006

% Beginn des eigentlichen Programms
h = ...

Unter der Annahme, dass dieses Programm im File secansh.m abgespeichert ist, liefert der Befehl help secansh die Zeilen

Funktion: secansh
Aufruf: h = secansh(x,x_0,s)
Berechnet fuer den Vektor x die Werte der normierten Secans Hyperbolicus 
Funktion mit dem Maximum bei x_0 und mit der Halbwertsbreite s
Input:  Vektor x, Skalar x_0, Skalar s
Output: Vektor h(x)

Name: Winfried Kernbichler
Datum: 15.02.2006

als Output am Schirm.

Solche Hilfetexte sollen bei allen Übungsbeispielen erstellt werden, manchesmal wird der Inhalt explizit überprüft. Dies wird aber in der Angabe zur Übung festgehalten.

disp

Formatierte Ausgabe am Schirm wird am einfachsten mit dem Befehl disp gemacht.

disp('Kernbichler')
name = 'Kernbichler'; disp(name)

gibt in beiden Fällen die Zeichenkette (string)

Kernbichler

aus.

Skalare, Vektoren, Matrizen können natürlich auch mit disp ausgegeben werden. So liefert

n = 5; disp(n) % Skalar
    5

z = 1:5; disp(z) % Zeilenvektor
    1     2     3     4     5

s = z.'; disp(s) % Spaltenvektor; z.' bedeutet transpose(z)
    1
    2
    3
    4
    5

o = ones(3,4); disp(o)
    1     1     1     1
    1     1     1     1
    1     1     1     1

Will man die Ausgabe von Zahlen mit der Ausgabe von Zeichen kombinieren, muss man die Zahlen in Zeichen verwandeln. Dazu gibt es unter anderem die Befehle num2str und mat2str. Damit kann man schreiben:

disp(['n = ',num2str(n)])
    n = 5

disp(['v = ',num2str(v)]) 
    v = 1  2  3  4  5

Die Klammern [] verbinden mehrere Zeichenketten zu einer

str1 = 'Mein'; str2 = 'Name';
str3 = [str1,str2]; disp(str3)
    MeinName

str3 = [str1,' ',str2]; disp(str3) % Mit Leerzeichen
    Mein Name

Die Befehle

disp(['s = ',num2str(s)])
disp(['o = ',num2str(o)])

würden Fehler der Art

??? Error using ==> horzcat
All matrices on a row in the bracketed expression must have the same number of rows.

liefern, da man nicht Variablen mit einer verschiedenen Anzahl von Zeilen nebeneinandet verbinden kann. Hier kann man sich mit mat2str behelfen

disp(['s = ',mat2str(s)])
    v = [1;2;3;4;5]

disp(['o = ',mat2str(o)])
    o = [1 1 1 1;1 1 1 1;1 1 1 1]

wobei hier der Strichpunkt die Zeilen trennt.

Graphik

plot

Die einfachste Möglichkeit Kurven darzustellen bietet die Matlab-Funktion plot. In diesem Beispiel erzeugt man mit linspace einen Vektor x_d mit n Zahlen zwischen x_s und x_e, berechnet dann für all diese Werte die Funktion sin und stellt die Werte in Form einer Kurve dar.

x_s = -pi; x_e = pi; n = 400;
x_d = linspace(x_s,x_e,n);
y_1 = sin(x_d);
plot(x_d,y_1);

Natürlich kann man das Aussehen der Kurve selbst bestimmen. Eine Zusammenfassung über die verschiedenen Spezifikationen für Linien liefert Informationen über Linienart, Markierungen, Farben, Liniendicke, usw.. So kann man obige Linie z.B. rot und strichliert zeichnen:

plot(x_d,y_1,'r--');

Will man mit dem Befehl plot mehrere Linien in einem Achsensystem zeichen, hat man zwei Möglichkeiten. Man kann die Anweisungen in einer Zeile schreiben

y_2 = cos(x_d);
plot(x_d,y_1,x_d,y_2);  % Ohne Angabe von Linienspezifikationen
plot(x_d,y_1,'r-',x_d,y_2,'b:'); % durchgehend rot, punktiert blau

oder als Folge von Anweisungen

plot(x_d,y_1,'r-'); % erste Linie; löscht vorhandenes Achsensystem
hold on % Modus "Hinzufügen"
plot(x_d,y_2,'b:'); % zweite Linie; zeichnet in das bereits vorhandene Achsensystem
hold off % beendet Modus "Hinzufügen"

Der Befehl hold schaltet dabei zwischen dem Modus zum Hinzufügen (on) und zum Neuzeichnen (off) um.

Matlab selbst bietet auch eine Einführung in die einfache Erstellung von Graphiken.

Ein Überblick über einige Möglichkeiten für einfache Graphiken wurde in diesem Matlab Skript zusammengestellt.

Vektoren mit NaN

Die Zahl nan ist besonders praktisch, wenn man Zeichnungen mit unterbrochenen Linien machen willl, die aber trotzdem eine Einheit (ein Graphikobjekt) bilden sollen. Zum Thema Rechnungen mit nan gibt es auch diesen Eintrag.

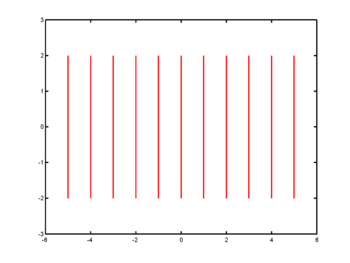
Als Beispiel seien hier 10 parallele Strecken angeführt, die in der Graphik selbst nicht verbunden sind, die aber eine Linie darstellen sollen. Das folgende Program erledigt diese Aufgabe

n = 11; a = 5; b = 2; 
x_v = linspace(-a,a,n);   % (1 x n)-Vektor von -a bis a
y_v = zeros(1,n) + b;     % (1 x n)-Vektor mit b
nan_v = nan(1,n);         % (1 x n)-Vektor mit NaNs
x_m = [ x_v; x_v; nan_v]; % (3 x n)-Matrix
y_m = [-y_v; y_v; nan_v]; % (3 x n)-Matrix
x = x_m(:); % Spaltevektor: -5,-5,nan,-4,-4,nan,..., 5,5,nan
y = y_m(:); % Spaltevektor: -1, 1,nan,-1, 1,nan,...,-1,1,nan
ph = plot(x,y); % Plot einer Linie
set(ph,'Color','r')
xlim([-a-1,a+1]); ylim([-b-1,b+1]);

Parallele Linien in einem Objekt

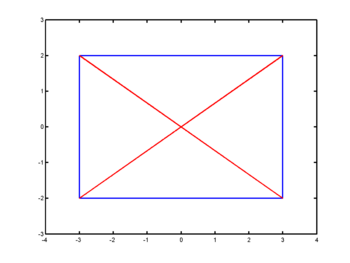
Ein anderes Beispiel zeichnet einen blauen Kasten und ein rotes Kreuz. Das Kreuz wird von links unten (-a,-b) nach rechts oben (a,b) und dann von links oben (-a,b) nach rechts unten (a,-b) gezeichnet. Wegen der Präsenz nan in den Vektoren wird die Linie von (a,b)->(-a,b) nicht gezeichnet. Beachte auch die Duplizierung des ersten Punktes am Ende der Vektoren für den Kasten. Damit wird eine geschlossene Linie erzeugt.

a = 3; b = 2;
xkasten = [a,-a,-a,a,a]; % Fuer geschlossene Linie
ykasten = [b,b,-b,-b,b];
plot(xkasten,ykasten,'b'); % Beginn bei (a,b), Ende bei (a,b)
xkreuz = [-a,a,nan,-a,a];
ykreuz = [-b,b,nan,b,-b];
hold on, plot(xkreuz,ykreuz,'r'); hold off % Hizufuegen des Kreuzes
xlim([-a-1,a+1]); ylim([-b-1,b+1]);

Kasten und Kreuz

polar

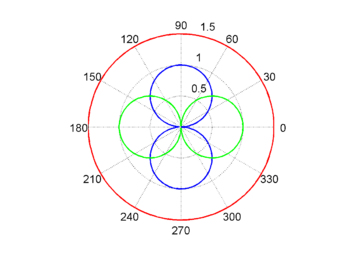
Im Gegensatz zum Befehl plot, der in einem kartesischen Koordinatensystem zeichnet, macht der Befehl polar seine Darstellung in Polarkoordinaten. Dies sei an folgendem Beispiel demonstriert, das einen Kreis

n = 100; a = 1.5;
phi = linspace(0,2*pi,n);  % phi-Vektor
r_k = ones(size(phi)) * a; % Radius-Vektor (gleich gross)
polar(phi,r_k,'r')         % Kreis

und zwei weitere Kurven darstellt. Hier sieht man einen weiteren Unterschied zu plot, da man bei polar nicht mit einem Aufruf mehrere Kurven zeichnen kann. Hier ist unbedingt die Verwendung von hold notwendig.

r_s = abs(sin(phi));
r_c = abs(cos(phi));
polar(phi,r_s,'b') % stehende Acht
hold on % Hinzufuegen eingeschaltet
polar(phi,r_c,'g') % liegende Acht
hold off % Hinzufuegen ausgeschaltet

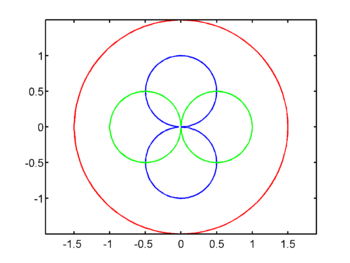
Will man das Gleiche mit plot machen, muss man die Vektoren in ein kartesisches Koordinatensystem umrechnen:

x_k = r_k .* cos(phi); y_k = r_k .* sin(phi); % Kreis
x_s = r_s .* cos(phi); y_s = r_s .* sin(phi); % stehende Acht
x_c = r_c .* cos(phi); y_c = r_c .* sin(phi); % liegende Acht
plot(x_k,y_k,'r',x_s,y_s,'b',x_c,y_c,'g')
axis 'equal' % Verhindert Verzerrung

Kreis und zwei Achter (polar)

Kreis und zwei Achter (plot)

Der Unterschied zwischen den Zeichnungen sollte evident sein.

Zum Umrechnen zwischen den Koordinatensystemen gibt es auch die Matlab-Befehle pol2cart und cart2pol.

fill

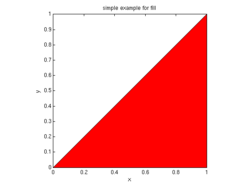
Mit fill lassen sich Bereiche in einem Plot einfärben. fill erwartet zwei Vektoren, die den Rand des zu füllenden Bereiches vorgeben als Input. Als drittes Argument ist noch die Farbe anzugeben. Einige Farben können als String (siehe fill), beliebige als [r g b]-Vektor angegeben werden.

%Beisp. zu fill; 
x = [0 1 1] ;
y = [0 0 1] ;
figure
fill(x,y,'r') ;
axis square; xlabel('x'); ylabel('y'); title('simple example for fill');

figure
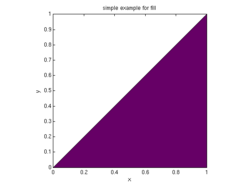
fill(x,y,[0.4 0 0.4])
axis square; xlabel('x'); ylabel('y'); title('simple example for fill');

pcolor vs. surf

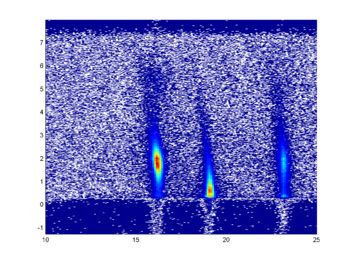
Oft wird zur Erzeugung von 2 dimensionalen Falschfarbenbilder surf verwendet und anschließend durch view(2) von oben auf die Fläche geschaut. surf ist allerdings nicht auf diese Art von Darstellung ausgelegt und es kann dabei zu gravierenden Rendering-Problemen kommen (z.B. bei der Darstellung von verrauschten Daten).

surf(x,y,z); view(2); shading flat

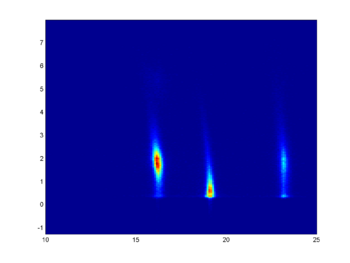
pcolor ist auf diese Anwendung ausgelegt und in der Regel werden damit bessere Ergebnisse erzielt. Zusätzlich geht pcolor sparsamer mit Ressourcen um.

pcolor(x,y,z); shading flat

Programmeinheiten

Skript

Ein Matlab-Skript läuft im Workspace ab und kann alle Variablen im Workspace verwenden und verändern. Somit verhält es sich nicht anders, als wenn man die Befehle Zeile für Zeile eingeben würde. Es stellt somit nur eine Vereinfachung gegenüber der händischen Eingabe dar, da man die Befehle abspeichern und somit immer wieder aufrufen kann.

Funktion

Im Unterschied zu einem Skript läuft eine Matlab Funktion in einem abgeschlossenen Arbeitsbereich ab und kann daher nicht auf Variablen im Basis-Workspace zugreifen oder diese verändern.

Eine Funktion braucht eine Deklarationszeile am Anfang

function out = name_func(in1,in2,in3,...)
function [out1,out2,out3,...] = name_func(in1,in2,in3,...)

mit dem Keyword function, den Namen der Outputvariablen, einem =, dem Namen der Funktion und den Namen der Inputvariablen.

So würde die Funktion

function res = test(a,b)
% Wurzel aus der Summe der Quadrate von a und b
% Name des Autors
% Datum
res = sqrt(a.^2 + b.^2);

die Wurzel aus der Summe der Quadrate von a und b berechnen. Der erste Block von Kommentarzeilen wird beim Aufruf von

help test

ausgegeben.

Die Werte von a und b werden erst beim Ausführen der Funktion übergeben

r_1 = test(1,2);  % a wird 1, b wird 2, r_1 wird sqrt(5) (innerhalb res)

oder

x = 2;
y = 3;
r_2 = test(x,y);  % a wird 2 (x), b wird 3 (y), r_2 wird sqrt(13) (innerhalb res)

Die Namen der Variablen innerhalb der Funktion und ausserhalb können gleich sein, müssen es aber nicht. Auch bei gleichen Namen haben die Variablen nichts miteinander zu tun, da sie in verschiedenen Workspaces (Arbeitsbereichen) existieren. Der Austausch findet nur über die Übergabeparameter (Input und Output) statt. Wäre der Ablauf also

a = 10; b = 20; x = 2; y = 3;
r_2 = test(x,y);  % a in test wird 2 (x), b in test wird 3 (y), r_2 wird sqrt(13) (innerhalb res)
disp(a) % ist noch immer 10, da in einem anderen Workspace
disp(b) % ist noch immer 20

Fehler und Warnungen

Es empfiehlt sich ungültige Funktionsaufrufe mit Hilfe der Funktion error anzuzeigen.

if Bedingung, error ('Fehlertext'); end
restliches Programm

Wenn im Programm der Befehl error ausgeführt wird, wird der Fehlertext ausgegeben und dann das Programm beendet. Daher ist es nicht notwendig, das Program in folgender Form zu schreiben

if Bedingung
  error ('Fehlertext')
else
  restliches Programm
end

Eine Warnung kann auf die gleiche Art mit der Funktion warning erzeugt werden. Bei einer Warnung wird der Text ausgegeben und dann wird das Programm fortgesetzt, also nicht wie bei einem Fehler unterbrochen.

Setzen von Defaultwerten

In Abhängigkeit von der Anzahl der Inputparameter mit der Funktion nargin:

function [o1,o2] = foo(a,b,c)
if nargin < 1, a = 4; end
if nargin < 2, b = 2; end
...

Setzen eines Defaultwertes wenn Parameter als leeres Feld [] übergeben wird (isempty):

function [o1,o2] = foo(a,b,c)
if isempty(a), a = 4; end
if isempty(b), b = 2; end
...

Dies ermöglicht den Aufruf einer Funktion auf folgende Weise:

[o1,o2] = foo(a,[],c);

Hier werden also für a und c Werte übergeben, und für den zweiten Parameter der Defaultwert verwendet. Dies ist mit der alleinigen Verwendung von nargin nicht möglich.

Eine Kombination von nargin und isempty:

function [o1,o2] = foo(a,b,c)
if nargin < 1, a = 1; end, if isempty(a), a = 1; end
if nargin < 2, b = 3; end, if isempty(b), a = 3; end

Eine kürzere Schreibweise ist mit Hilfe des Short-circuit OR möglich:

function [o1,o2] = foo(a,b,c)
if nargin < 1 || isempty(a), a = 1; end
if nargin < 2 || isempty(b), b = 3; end
...

Eine ausführlichere Zusammenstellung finden Sie im Skriptum in Kapitel 9.

Siehe dazu auch die Erläuterungen zum Befehl if.

Handle auf Funktionen

Ein function_handle stellt eine Referenz auf eine Funktion dar. Referenz bedeutet vereinfacht dargestellt, dass eine (Matlab oder selbst geschriebene) Funktion über einen alternativen Namen angesprochen werden kann. Einen großer Vorteil ist, dass ein function_handle an eine Funktion als Parameter übergeben werden kann. Dies soll hier aber nicht weiter erläutert werden (siehe Matlab-Dokumentation unter function_handle)

Es ist auch möglich einen function_handle derart zu definieren, dass die "Funktion" nur über diesen ansprechbar ist. Dies nennt man dann einen Handle auf eine anonyme Funktion. Dies ist sehr praktisch, da man damit einfache Funktionen (ähnlich zu inline-Funktionen) direkt in einem Skript definieren kann. Ein Vorteil von function_handles gegenüber inline-Funktionen ist, dass sie einfacher miteinander kombiniert und modifiziert werden können.

Beispiel

% Definition eines Handles auf eine anonyme Funktion
   mod_fun = @(A,x) A*(x.^2+x.^3) ;
% Definition eines weiteren Handles, der sich vom ersten durch die Reihenfolge
% der Parameter unterscheidet.
   fun_han = @(x,A) mod_fun(A,x) ;
% Berechnung
   A = 5 ;
   x = linspace(-1,1,50) ;
   y1 = mod_fun(A,x) ;
   y2 = fun_han(x,A) ; 
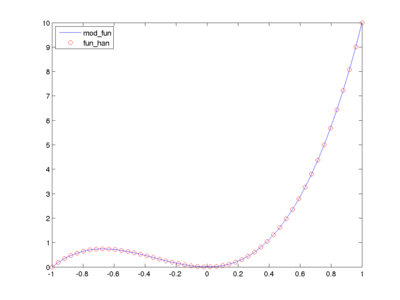
% Visualisierung ergibt hier natürlich das gleiche
   plot(x,y1,x,y2,'ro') ;
   legend('Location','NW',{'mod\_fun','fun\_han'}) ;

Sie sehen, dass es möglich ist den function_handle auch für weitere Definitionen zu verwenden. Hier wurde z.B. bei der Definition von fun_han die Reihenfolge der Eingabeparameter vertauscht (Die Reihenfolge hinter @ ist maßgeblich).

Noch ein Beispiel

% Definition
   mod_fun = @(A,x) A*(x.^2+x.^3) ;
   A = 5 ;
   fun_han = @(x) -mod_fun(A,x) ;
% Berechnung
   x = linspace(-1,1,50) ;
   y1 = mod_fun(A,x) ;
   y2 = fun_han(x) ;
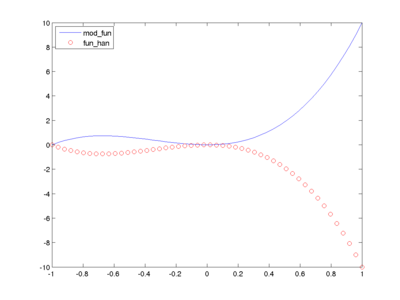
% Visualisierung
   plot(x,y1,x,y2,'ro') ;
   legend('Location','NW',{'mod\_fun','fun\_han'}) ;

Hier unterscheidet sich fun_han durch 2 Eigenschaften von mod_fun

1. wurde mod_fun mit -1 multipliziert.
2. wurde fun_han so erzeugt, dass A keinen Inputparamter mehr darstellt. In diesem Fall muss die Variable A existieren, bevor der Handle definiert wird. Der Wert den A zu diesem Zeitpunkt hat wird dann fix in die Funktion integriert. Ändern Sie A nach der Definition und rufen fun_han nochmal auf ändert sich das Ergebnis nicht.

Beispiel:

   A = 5 ;
   fun_han = @(x) A*sin(x) ;
   fun_han(pi/2) ; % -> 5
   A = 2 ;
   fun_han(pi/2) ; % -> IMMER NOCH 5 !!!
% aber
  fun_han = @(x) A*sin(x) ;
  fun_han(pi/2) ; % -> 2

Wollen Sie den function_handle an eine Funktion übergeben, so können Sie den function_handle direkt beim Aufruf der Funktion definieren:

   A = 5 ;
   flaeche = quadl(@(x) A*(x.^2+x.^3) ,0,10) ;

Leerer Übergabeparameter:

   A = 5; x = 1:3; 
   fun_t = @() A*x;

Hier gibt es keine Übergabeparameter, da A und x schon vorher definiert sind. Sowohl bei der Definition als auch bei der Ausführung muss das Klammerpaar () verwendet werden.

   y = fun_t()  % -> liefert [5 10 15]
   f = fun_t    % -> @() A*x

wobei die erste Zeile das gewünschte Ergebniss der Rechnung liefert und die zweite Zeile eine Kopie der Funktion erzeugt, die danach wie die ursprüngliche Funktion verwendet werden kann (f()).

Weitere Information finden Sie in der Matlab-Hilfe unter:

• http://itp.tugraz.at/matlab/techdoc/ref/function_handle.html
• http://itp.tugraz.at/matlab/techdoc/matlab_prog/ch_func3.html

Steuerstrukturen

if

Eine einfache Entscheidung, kann in Matlab mit if getroffen werden,

if "Bedingung"
    "Das tue ich, wenn die Bedingung erfuellt ist"
end

also z.B.,

if a < 3
    disp('a ist kleiner als 3')
end

Wenn also die Variable a einen Wert hat der kleiner als 3 ist, wird die Zeile ausgegeben, sonst passiert nichts. Die Bedingung muss entweder wahr (1) oder falsch (0) sein, also eine logische Information enthalten. Das Ganze kann natürlich mit elseif bzw. else weiter ausgebaut werden

if a < 3 % Erste Bedingung
    disp('a ist kleiner als 3')
elseif a > 3 % Zweite Bedingung
    disp('a ist groesser als 3')
else % Der Rest
    disp('a ist gleich 3')
end

Siehe dazu auch die Erläuterungen zum Setzen von Defaultwerten.

Als Bedingung sind alle Matlab-Ausdrücke erlaubt, die wahr oder falsch ergeben

if isempty(x) % wenn x ein leeres Feld ist
if isempty(x) || isempty(y) % oder
if isempty(x) && isempty(y) % und
if all(isnan(x)) % wenn alle Werte in x NaN sind
if any(isnan(x)) % wenn zumindest ein Wert in x NaN ist
if ~any(isnan(x)) % wenn kein Wert in x NaN ist 
if not(any(isnan(x))) % wenn kein Wert in x NaN ist

Siehe dazu auch die Erläuterungen zum Logische Verknüpfungen mit Short Circuit.

switch

Die switch-Konstruktion eignet sich am besten zur Auswahl zwischen einzelnen Fällen, die abgearbeitet werden sollen. Sie benötigt eine Schaltervariable und dann verschiedene unterschiedliche Fälle (case).

switch schalter
  case 1
    "Das tue ich, wenn die Variable schalter den Wert 1 hat"
  case 2
    "Das tue ich, wenn die Variable schalter den Wert 2 hat"
  case 3
    "Das tue ich, wenn die Variable schalter den Wert 3 hat"
end

Es wird maximal ein Fall (der erste der passt) abgearbeitet. Wenn keiner passt, wird nicht getan.

Das geht auch mit Zeichen bzw. Zeichenketten

switch typ
  case 'Kreis'
    "Das tue ich, wenn die Variable schalter den Wert 'Kreis' hat"
  case 'Ellipse'
    "Das tue ich, wenn die Variable schalter den Wert 'Ellipse' hat"
  case 'Hyperbel'
    "Das tue ich, wenn die Variable schalter den Wert 'Hyperbel' hat"
end

In einem case können mehrere Varianten vorkommen:

switch typ
  case {'Kreis','kreis','K','k'}
    "Das tue ich, wenn die Variable schalter den Wert 'Kreis', 'kreis', 'K' oder 'k' hat"
end

Mit Hilfe der Erläuterungen über Zeichenketten sollte man nun auch die Variante

switch lower(typ(1))
  case 'k'
    "Das tue ich, wenn die Variable schalter einen Wert hat, der mit 'k' bzw. 'K' beginnt"
  case 'e'
    "Das tue ich, wenn die Variable schalter einen Wert hat, der mit 'e' bzw. 'E' beginnt"
  case 'h'
    "Das tue ich, wenn die Variable schalter einen Wert hat, der mit 'h' bzw. 'H' beginnt"
end

Ein einfaches Beispiel kann also so aussehen

typ = 'Hyperbel';
switch lower(typ(1))
  case 'k'
    disp('Ich bin ein Kreis')
  case 'e'
    disp('Ich bin eine Ellipse')
  case 'h'
    disp('Ich bin eine Hyperbel')
end

Matlab würde nun mit

'Ich bin eine Hyperbel'

antworten.

otherwise

Im obigen Beispiel, werden nur jene Fälle abgehandelt, die mit einem der definierten cases übereinstimmt. Will man in allen anderen Fällen, wenn es also keine Übereinstimmung gibt, einen Programmteil ausühren, dann muss man otherwise verwenden.

Obiges Beispiel würde für

typ = 'Gerade';

nichts tun, da 'g' nicht in der Liste der Fälle vorkommt. Modifiziert man aber das Beispiel

typ = 'Gerade';
switch lower(typ(1))
  case 'k'
    disp('Ich bin ein Kreis')
  case 'e'
    disp('Ich bin eine Ellipse')
  case 'h'
    disp('Ich bin eine Hyperbel')
  otherwise
    disp('Fall nicht definiert')
end

würde Matlab mit

'Fall nicht definiert'

antworten.

for

In einer for-Schleife existiert eine Zählvariable, die nacheinander vorgegeben Werte (bis zu einem vorab bekannten Maximalwert) annimmt.

n = 5;
x = zeros(1,5) % Eine Zeile mit fünf Spalten; alles Null
for k = 1:n;
    x(k) = k^2;
end

Dies würde also einen Vektor x = [1^2, 2^2, 3^2, 4^2, 5^2] = [1, 4, 9, 16, 25] ergeben.

Berechnung einer Summe

Die for-Schleife kann auch verwendet werden um eine Summe zu berechnen.
Beispiel:
Die Summe [math] S = \sum_{k=0}^5 x^k [/math] läßt sich folgendermaße berechnen:

...
S = 0;
for k = 0:n
    S = S + x^k ;
end
...

Besser verwendet man dafür natürlich den Befehl sum.

Operatoren

Elementweise Operationen

Einige arithmetische Operatoren nämlich

* / \ ^

gibt es auch in der Form

.* ./ .\ .^

wobei diese Form für die elementweise Anwendung des Operators bestimmt ist. Die Form ohne Punkt ist für Matrizenoperationen zuständig.

Will man also die Vektoren

x = 0:5
y = 10:15

elementweise miteinander multiplizieren, muss man schreiben

r = x .* y

Das Gleiche gilt für

r = x ./ y; r = x.^y; r = x .\ y

Ist ein Partner ein Skalar kann man oft beide Formen verwenden

x .* 2 oder x * 2
2 .* x oder 2 * x
x ./ 2 oder x / 2
2 ./ x aber nicht 2 / x
x .\ 2 aber nicht x \ 2
2 .\ x oder 2 \ x
x .^ 2 aber nicht x ^ 2
2 .^ x aber nicht 2 ^ x

Für Plus (+) und Minus (-) gibt es aus verständlichen Gründen keine Version mit einem Punkt

Vergleichsoperationen

Wie alle Operatoren in Matlab kann man auch die Vergleichsoperatoren auf Matrizen und Vektoren anwenden. Hat man also z.B. die Vektoren

x = 1 2 3
y = 3 2 1

so liefert

x <  y   %  1 0 0 (kleiner)
x <= y   %  1 1 0 (kleiner gleich)
x >  y   %  0 0 1 (größer)
x >= y   %  0 1 1 (größer gleich)
x == y   %  0 1 0 (gleich)
x ~= y   %  1 0 1 (nicht gleich)

wobei 1 (Eins) für Wahr und 0 (Null) für Falsch steht. Das Ergebnis sind also logische Variablen.

Einer oder beide der zu vergleichenden Größen kann natürlich auch ein Skalar sein:

x <  2   %  1 0 0 (kleiner)
x <= 2   %  1 1 0 (kleiner gleich)
x >  2   %  0 0 1 (größer)
x >= 2   %  0 1 1 (größer gleich)
x == 2   %  0 1 0 (gleich)
x ~= 2   %  1 0 1 (nicht gleich)

Die Regel ist also ganz einfach, entweder sind beide Partner Felder mit gleicher Größe oder zumindest ein Partner ist ein Skalar.

Logische Verknüpfung von Vergleichsoperationen

Hierzu existieren die logischen Operatoren.

x = 1 2 3 1
y = 3 2 1 4

x == 1 & y == 3 % AND [1 0 0 1] & [1 0 0 0] => [1 0 0 0]
x == 1 | y == 2 % OR  [1 0 0 1] & [0 1 0 0] => [1 1 0 1]

Logische Verknüpfungen mit Short Circuit

Die Short Circuit Operatoren lauten || und &&. Hier wird die Abarbeitung des Ausdrucks beendet, sobald der Ausgang klar ist.

x = true;
y = false;

if x || y, disp('mindestens eines wahr'); end

Hier wird der Wert von y gar nicht mehr überprüft, da der gesamte Ausdruck auf jeden Fall true (1) sein wird. Bei && verhält es sich natürlich genau umgekehrt.

if y && x, disp('beide wahr'); end;

Hier wird x nicht mehr überprüft, da der Gesamtausdruck auf jeden Fall false (0) sein wird. Bei der ursprünglichen Reihenfolge

if x && y, disp('beide wahr'); end 

müssen natürlich beide Variablen überprüft werden, damit ein Urteil gefällt werden kann, da bei einem Wert true für die Variable x die Entscheidung vom Wert für y abhängt.

Für eine Anwendung des Short-Circuit OR siehe MLTutor_-_Hints#Setzen_von_Defaultwerten

Besondere Zahlen

NaN

DIe Zahl nan oder auch NaN steht für "Not a Number", ist also eigentlich keine Zahl, sondern eine Art Platzhalter.

Matrizen, sofern sie nicht insgesamt leer sind, müssen ja an jeder Position einen Wert haben. Will man dafür eine unbestimmte Zahl verwenden, bietet sich nan an

x = [1, 2; 3, nan]

liefert als Ergebnis die (2x2)-Matrix

1 2
3 nan

Damit kann man alle beliebigen Rechnungen machen, wobei die Regel gilt: Arithmetische Operationen mit nan liefern wieder nan:

y = x*2

liefert also

2 4
6 nan

Auch mathematische Funktionen angewandt auf NaN liefern NaN

sin(nan)   ->   nan

Will man eine (nxm)-Matrix mit lauter NaNs schaffen, kann man

m = 3; n = 4; nan_matrix = zeros(m,n) + nan;

schreiben.

Vergleiche mit NaN liefern immer den Wert "falsch" (0):

3 < nan   ->   0
nan == nan   ->   0

Will man also wissen, ob ein Ergebnis NaN ist, muss man die Funktion isnan verwenden. Angewandt auf obiges Beispiel bekommt man damit für

was_ist_nan = isnan(x)

das Ergebnis

0 0
0 1

bzw. für

was_ist_nicht_nan = ~isnan(x)

das Ergebnis

1 1
1 0

Zum Thema Plotten mit nan gibt es auch diesen Eintrag.

Komplexe Zahlen

In den neuesten Versionen von Matlab wird für den Imaginärteil von komplexen Variablen folgende Schreibweise

z = 5 + 3i
z = 5.1 + 3.7i
z = 5.1 + 1e-5i    % 1e-5 ist die Exponentialdarstellung für 0.00001 (10^(-5))

empfohlen. Dies ersetzt die alte Schreibweise

z = 5 + 3*i
z = 5.1 + 3.7*i
z = 5.1 + 1e-5*i

und behebt damit die Schwierigkeiten wenn die imaginäre Einheit i z.B. als Zählvariable verwendet wird. Dann liefern nämlich die Befehle

i = 4
z = 5 + 3*i

den korrekten aber vielleicht ungewollten Wert

5 + 3*4 = 17

während

i = 4
z = 5 + 3i

wirklich das komplexe Resultat

z = 5 + 3i

liefert. Damit ist ganz klar der Vorteil der neuen Schreibung definiert. Natürlich ist es aber eine Ausnahme von der Regel, dass Variablen nicht ohne Operator aneinander gereiht werden dürfen, da man ja auf keinen Fall

x = i; z = 5 + 3x

schreiben dürfte und man folgenden Fehler bekommt:

z = 5 + 3x Error: Unexpected MATLAB expression.

Im Ausnahmefall der komplexen Zahlen ist also 5i als Einheit zu verstehen. Das Gleiche gilt jedoch nicht bei einem Umdrehen der Schreibung. Hier liefert

z = 5 + i3

natürlich den Fehler

Undefined function or variable 'i3',

da i3 natürlich als Variable aufgefasst wird.

Praktische Funktionen

atan2

Die Umrechnung zwischen kartesischen Koordinaten und Polarkoordinaten erfolgt folgenden Formeln:

Umrechnung

[math]x = r\;\cos \phi[/math],	[math]y = r\;\sin \phi[/math]
[math]r = \sqrt{x^2 + y^2}[/math],	[math]\phi = \arctan\frac{y}{x} [/math]

Bei der Umrechnung von Polarkoordinaten zu kartesischen Koordinaten gibt es keine Probleme. Probleme kann es aber bei der Berechnung des Winkels [math]\phi[/math] geben, da die Funktion [math]\arctan[/math] im Intervall [math][0,2\pi][/math] nicht eineindeutig ist. Das soll an folgendem Beispiel demonstriert werden:

n = 200;
p_k = linspace(0,2*pi,n);  % phi-Vektor
r_k = ones(size(p_k)); % Radius-Vektor (gleich gross) 
% Transformation zu kartesichen Koordinaten
x_k = r_k .* cos(p_k); 
y_k = r_k .* sin(p_k);
% Ruecktransfromation
r_r = sqrt(x_k.^2 + y_k.^2);
p_r1 = atan(y_k./x_k);
p_r2 = atan2(y_k,x_k);
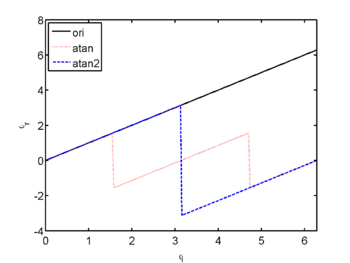
plot(p_k,p_k,'k-',p_k,p_r1,'r:',p_k,p_r2,'b--')
xlabel('\phi'); ylabel('\phi_r');
legend({'ori','atan','atan2'},'Location','nw')
xlim([0,2*pi])

Rücktransformation

Die Funktion atan liefert immer Werte im Intervall [math][-\pi/2,\pi/2][/math] und eignet sich daher nicht für die Transformation. Die Funktion atan2 liefert die Werte im Intervall [math][-\pi,\pi][/math] und eignet sich dager bestens für die Zuordnung zu den einzelnen Quadranten.

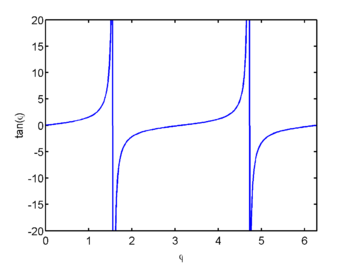
Der Plot von [math]\tan\phi[/math] zeigt die Nicht-Eineindeutigkeit dieser Funktion

plot(p_k,tan(p_k))
xlabel('\phi'); ylabel('tan(\phi)'); xlim([0,2*pi]); ylim([-20,20])

Tangens

Zeichenketten

Zeichenketten in Matlab sind nichts anderes als Vektoren (Matrizen) von Zeichen. Man kann daher mit einem Index auf einzelne Zeichen zugreifen

s = 'Kreis';
s(1)   ->   'K'
s(2)   ->   'r'

Es gibt eine Menge praktischer Funktionen für die Verarbeitung solcher Zeichenketten, wie z.B., die Umwandlung in Klein- oder Großbuchstaben mit lower bzw. upper.

kl = lower(s)   ->   'kreis'
gr = upper(s)   ->   'KREIS'

Praktisch sind diese einfachen Funktionen bei der Verwendung von Schaltern.

Links

Folgende Linkarten sind vordefiniert:

mltutor://Projektname	Interner Link zu MLTutor Projekt
matref://Funktionsname	Link zu Matlab Hilfe wird zu http://itp.tugraz.at/matlab/techdoc/ref/sin.html
itpwiki://Wikieintrag	Link zu ITP Wiki
appsoftkapitel://7	Link zu Applikationssoftwareskriptum Kapitel 7
appsoftskriptum	Link zu Applikationssoftwareskriptum