Matlab - Fehler

In jeder Programmiersprache, so auch in Matlab, gibt es eine Reihe von Fehlermöglichkeiten, die dazu führen, dass das Programm scheinbar ordnungsgemäß beendet wird. Trotzdem ist das Ergebnis falsch oder zumindest entspricht es nicht den Erwartungen. Einige dieser Fehler sind lustig, andere für Anfänger oft verblüffend.

Sie können hier zu einer Sammlung und Beschreibung dieser Fehler beitragen, da ich glaube, dass man daraus sehr viel lernen kann.

Verwechslung von : und ;

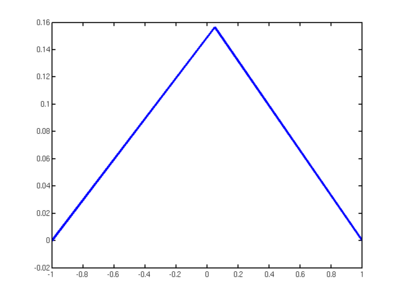
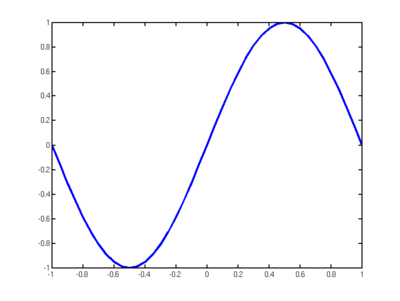
Ein Plot der Funktion f(x) = sin(π x) im Intervall [-1,1] wurde mit folgendem Code versucht:

x = [-1;0.05;1]; y = sin(pi*x); plot(x,y)

Dabei wurden die Zeichen ; und : verwechselt. Der richtige Code müsste daher so lauten:

x = [-1:0.05:1]; y = sin(pi*x); plot(x,y)

Der Grund, das Matlab hier keine Fehlermitteilung liefert, liegt darin, dass zwar für das gewünschte Ziel ein falscher Befehl verwendet wurde, dieser Befehl aber eine korrekte Syntax hat:

x = [-1;0.05;1]   Spaltenvektor    [-1
                                     0.05
                                     1]
x = [-1,0.05,1]   Zeilenvektor     [-1 0.05 1]
x = [-1:0.05:1]   Bereich von bis  [-1 -0.95 -0.9 ... 0.9 0.95 1]

Überprüfung von Übergabeparametern

Aufgabenstellung

Es soll eine MATLAB-Funktion test geschrieben werden, die für den zweiten Inputparameter einen Defaultwert von 5 setzt und zwar für den Fall wenn dieser nicht übergeben wird oder wenn er leer [] ist.

Mögliche Lösungen

• Zwei getrennte bedingte Anweisungen, wobei die Variable nargin dabei als Zähler für die Anzahl der übergebenen Inputparameter fungiert.

function r = test(a,b)
bd = 5; % Defaultwert für b
if nargin < 2, b = bd; end
if isempty(b), b = bd; end
r = a + b;

Fehler: Vertauschung der beiden bedingten Anweisungen

if isempty(b), b = bd; end
if nargin < 2, b = bd; end

• Zwei gekoppelte bedingte Anweisungen

function r = test(a,b)
bd = 5; % Defaultwert für b
if nargin < 2
  b = bd;
elseif isempty(b)
  b = bd;
end
r = a + b;

Fehler: Vertauschung der beiden bedingten Anweisungen

if isempty(b)
  b = bd;
elseif nargin < 2
  b = bd;
end

• Lösung mit einer bedingten Anweisung unter Verwendung des Befehls or in seiner "short circuit" Version ||

function r = test(a,b)
bd = 5; % Defaultwert für b
if nargin < 2 || isempty(b), b = bd; end
r = a + b;

Fehler: Verwendung des normalen or Befehls |

if nargin < 2 | isempty(b), b = bd; end

Fehler: Falsche Verwendung des if-Befehls

if nargin < 2 || if isempty(b), b = bd; end
if nargin < 2, b = bd; || if isempty(b), b = bd; end

Fehler: Falsche Verwendung von isempty

if nargin < 2 || isempty, b = bd; end

• Alternative für nargin mit Hilfe des Befehls exist

function r = test(a,b)
bd = 5; % Defaultwert für b
if ~exist('b','var') || isempty(b), b = bd; end
r = a + b;

• Ergänzung um eine Fehlermitteilung

function r = test(a,b)
bd = 5; % Defaultwert für b
if nargin < 1 || isempty(a), error('a muss übergeben werden!'); end
if nargin < 2 || isempty(b), b = bd; end
r = a + b;

• Lösung mit variabler Inputliste, wobei varargin eine Zelle mit allen Inputparametern ist.

function r = test(varargin)
bd = 5;
a = varargin{1};
if nargin < 2 || isempty(varargin{2})
  b = bd;
else
  b = varargin{2};
end
r = a + b;

Aufruf

Nach Fertigstellung der Funktion kann man sie in folgender Weise aufrufen:

x = 1; y = 2;
r = test(x);      % b Default
r = test(x,[]);   % b Default
r = test(x,3);    % b = 3
r = test(x,y);    % b = 2

Nicht möglich ist folgender Aufruf

r = test(x,b);    % FALSCH!

da das aufrufende Programm die Variable b nicht kennt (verschiedene Workspaces)

Lieblingsfehler

Unter sanfter Vernachlässigung aller Informationen wurde das Problem so gelöst:

function r = test(a,b)
if nargin < 3, b = 5; end
b = input('Bitte geben sie b ein: ');
r = a + b;

Das Programm produziert keine Fehlermitteilung, überschreibt aber in der zweiten Zeile eine eventuelle Übergabe für b mit dem Wert 5 um diesen dann in der dritten Zeile mit einer Eingabe des Benutzers zu überschreiben.

Umsetzung von Funktionen

Einfacher Fall

Die Umsetzung einer simplen Funktion

[math] g(x) = \frac{1}{\sqrt{2\pi}\sigma} \exp(-\frac{(x-x_{0})^2}{2\sigma^2}) [/math]

erfolgt in MATLAB in einfachster Form mit

function g = gauss(x,x0,s)
g = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi)*s);

Interessante Fehlemöglichkeiten sind

• die Verwendung von x als Index

g(x) = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi)*s);

• die Verwendung eines falschen Operators (x ist ein Array)

g = exp(-(x-x0)^2/(2*s^2)) / (sqrt(2*pi)*s);

• das Vergessen von Klammern

g = exp(-(x-x0).^2/2*s^2) / (sqrt(2*pi)*s);

• die Erstreckung des Wurzelausdruckes auf andere Variablen

g = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi*s));

• die Inkonsistenz bei der Benennung von Variablen

function g = gauss(x,x_0,s)
g = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi)*s);

Fall mit mehreren Peaks

Will man nun die Funktion erweitern, so dass sie mehrere Peaks umfassen kann, dann kann man das in der Mathematik so schreiben:

[math] g(x) = \frac{1}{n} \sum_{k=1}^{n} \frac{1}{\sqrt{2\pi}\sigma_k} \exp(-\frac{(x-x_{0,k})^2}{2\sigma_k^2}) [/math],

wobei n die Anzahl der Peaks und k eine Art Zählvariable ist.

Der erste Versuch

function g = gauss(x,x0,s)
g = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi)*s);

schlägt fehl, da x0 und s nun Vektoren sind und man, z.B., zwei ungleich lange Vektoren nicht von einander subtrahieren kann.

Der zweite Versuch mit einer for-Schleife

function g = gauss(x,x0,s)
for k = 1:numel(x0)
  g = exp(-(x-x0).^2/(2*s^2)) / (sqrt(2*pi)*s);
end

schlägt fehl, da die Verwendung der Schleife noch nichts an der Formel geändert hat.

Die Einführung der Indizes x0(k) und s(k)

function g = gauss(x,x0,s)
for k = 1:numel(x0)
  g = exp(-(x-x0(k)).^2/(2*s(k)^2)) / ...
      (sqrt(2*pi)*s(k));
end

lässt das Programm laufen, liefert aber nur den letzten Peak als Ergebnis.

Die Idee, das man alle Peaks addieren muss

function g = gauss(x,x0,s)
for k = 1:numel(x0)
  g = g + exp(-(x-x0(k)).^2/(2*s(k)^2)) / ...
      (sqrt(2*pi)*s(k));
end

führt aber wieder zu einem Fehler, da beim ersten Durchlauf durch die Schleife g auf der rechten Seite nicht bekannt ist.

Die Initialisierung von g und die Division durch n am Ende

function g = gauss(x,x0,s)
n = numel(x0);
g = zeros(size(x));
for k = 1:n
  g = g + exp(-(x-x0(k)).^2/(2*s(k)^2)) / ...
      (sqrt(2*pi)*s(k));
end
g = g / n;

führt schließlich zum gewünschten Ergebnis, das man sich, z.B., mit

x = linspace(-5,5,1000);
plot(x, gauss(x, [-1,0,1], [0.5,0.3,1]) )

anschauen kann.