RLC-Serienschwingkreis
Inhaltsverzeichnis
Uebertragungsverhalten eines RLC-Serienresonanzkreis
Einleitung
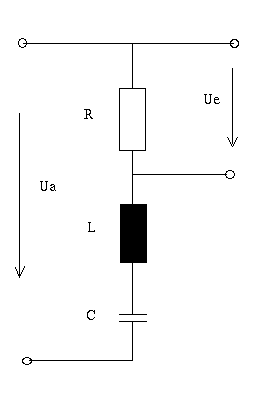
Ziel ist es das Uebertragungsverhalten eines RLC-Kreis darzustellen:
An einen Serienresonanzkreis wird ein periodisches Spannungssignal angelegt, wie sieht die Ausgangsspannung am Widerstand aus?
Hierzu wurden 2 verschieden Moeglichkeiten implementiert
- Fourierzerlegung - Uebertragungsfunktion:
Das Signal kann in seine Sinuskomponenten zerlegt, das Problem im Frequenzbereich geloest und fuer die Darstellung in den Zeitbereich transformiert werden - Simulation der Differentialgleichung:
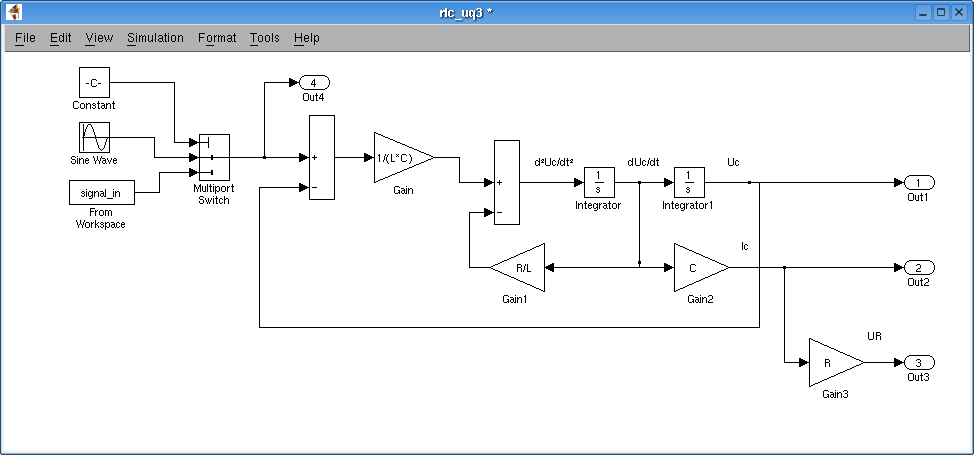
Die Differentialgleichung fuer einen Schwingkreis muss aufgestellt und mit Simulink simuliert werden.
Fourierzerlegung - Uebertragungsfunktion
Benutzeroberflaeche
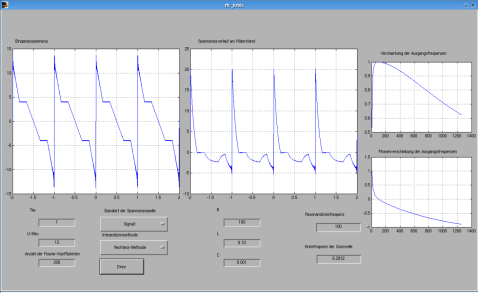
Benutzeroberflache vergroessern
- Einstellen der Periodendauer
- Einstellen der Maximalspannung der Spannungsquelle
- Hier kann man die Anzahl der Fourierkoeffizienten einstellen, die berechnet werden (max 200)
- Popupmenue zum einstellen der gewuenschten Signalform
- Popupmenue zum auswaehlen der Integrationsmethode bei der Berechnung der Fourierkoeffizienten
- Bauteilwerte des RLC Schwingkreises
- Errechnete Kreisfrequenz der Grundwelle des Sapnnungssignals und Resonanzkreisfrequenz des Serienschingkreises
- Spannungsverlauf der Spannungsquelle
- Spannungsverlauf am Widerstand
- Uerbertragungsfunktion: Verstaerkung und Phasenverschiebung in Abhaengigkeit von der Kreisfrequenz
- Berechnen der Signale
Fourierzerlegung
Als erster Schritt muss das Signal wenn es nicht-sinusfoermig ist mittels Fourier-Reihe angenaehert werden:
[math]u_q(t) = \frac{a_0}{2} + \sum_{i=1}^N(a_n\cos(n \omega_0 t)+b_n\sin(n \omega_0 t))[/math]
Kreisfrequenz der Grundwelle...[math]\omega_0 = \frac{2\pi}{\tau}[/math]
[math]a_0 = \frac{1}{\tau} \cdot \int_0^{\tau}u_q(t)dt[/math]
[math]b_n = \frac{1}{\tau} \cdot \int_0^{\tau}uq(t)\cdot \sin(n\cdot t)dt[/math]
da es sich bei unseren Signalen nur um ungerade Funktionen handelt die keinen Gleichanteil besitzen, muessen wir nur [math]b_n[/math] bestimmen,
[math]a_n[/math] sowie [math]a_0[/math] sollten 0 sein. Die Fourierkoeffizienten werden mittels numerischer-Integration errechnet
Uebertragungsfunktion
Nun muss noch die Uebertragunsfunktion [math]F\left( j\omega\right)[/math] aufgestellt werden:
Die Gesamtimpedanz der Schaltung ist: [math]Z_{ges} = R + j\omega L + \frac{1}{j\omega C}[/math]
Die Spannung am Widerstand kann mittels Spannungsteiler errechnet werden: [math]U_a = U_q \cdot \frac{R}{R + j\omega L + \frac{1}{j\omega C}}[/math]
Dies ergibt die Uebertragungsfunktion:
[math]F(j\omega ) = \frac{U_a}{Ue} = \frac{R}{R + j\omega L + \frac{1}{j\omega C}}[/math]
Nun kann fuer alle Kreisfrequenzen des Fourier zerlegeten Signals die Verstaerkung und Phasenverschiebung errechnet werden:
Verstaerkung :[math] k_n = |F(j\cdot n \cdot \omega_0)|[/math]
Phasenverschiebung : [math]\phi_n = Arg(F(j\cdot n \cdot \omega_0))[/math]
Das Signal am Widerstand ergibt sich somit zu:
[math]u_q(t) = \sum_{i=1}^N(k_n\cdot b_n\cdot \sin(\omega_0\cdot n \cdot t + \phi_n))[/math]
Simulation der Differentialgleichung:
Strom - Spannungsbeziehung fuer einen ohmschen Widerstand eine Induktivitaet und einen Kondensator
[math]u(t) = R\cdot i(t)[/math]
[math]u(t) = L \frac{di(t)}{dt}[/math]
[math]i(t) = C \frac{du(t)}{dt}[/math]
Aufstellen der DGL:
[math]u_R + u_L + u_C = u_q[/math]
[math]i_L = i_C[/math]
[math]u_L = L\cdot\frac{di_C}{dt} = LC \cdot \frac{d^2u_C}{dt^2}[/math]
[math]u_R = R\cdot i_C = RC \frac{du_C}{dt}[/math]
[math]\Rightarrow LC \cdot \frac{d^2u_C}{dt^2} + RC \frac{du_C}{dt} + u_C = u_q[/math]
[math]\Rightarrow \frac{d^2u_C}{dt^2}+ \frac{R}{L} \frac{du_C}{dt} + \frac{1}{LC}u_C = \frac{1}{LC} uq[/math]
Nachdem dies DGL ermittelt worden ist kann sie in Simulink modelliert und simuliert werden: