Selbstständig lernender Algorithmus

Projektidee

Trotz der immer höher werdenden Rechenleistungen der heutigen Computer, kann der Rechner nach wie vor nur die vom Programmierer vorgegebenen Befehle ausführen. Dieses Projekt startet einen Versuch einen primitiv selbstständig denkenden Algorithmus zu entwickeln, ohne die Theorie von neuronalen Netzen oder den Besitz eines Supercomputers vorauszusetzen.

Planungsphase

Vision

Es soll ein Algorithmus entwickelt werden, der in der Lage ist Gelerntes abzuspeichern und später darauf wieder zuzugreifen. Zu diesem Zweck wird das einfache Spiel Tic Tac Toe implementiert, bei welchem zwei Spieler abwechselnd Markierungen in ein Gitter einfügen und der Sieg durch eine durchgehende waagrechte, senkrechte oder diagonale Reihe erzielt wird. Grundsätzlich ist es üblich bei der Implementierung von künstlichen Gegnern dem Computer eine Strategie zur Erreichung eines Siegs fest vorzugeben und nach jedem Spielzug die Abfrage durchzuführen, ob ein Sieg oder eine Niederlage erreicht wurde.

Bei diesem Projekt sollen jedoch nur die Befehle für die Benutzerinteraktion und die Gewinnabfrage fest vorgegeben werden. Das System soll mit jedem Spiel lernen, ob die gewählten Züge gewinnbringend oder nicht waren und so mit der Zeit eine immer größere Spielzug-Datenbank aufbauen.

Grundkonzept des Algorithmus

Der menschliche Spieler und der Computer machen abwechselnd Züge, wobei die allerersten Züge des Computers völlig zufällig sind. Nach jedem Zug wird abgefragt, ob einer der beiden Kontrahenten einen Sieg erreicht oder das Spiel in einem Unentschieden geendet hat. Sollte der Benutzer gewonnen haben (wovon bei den ersten Runden natürlich auszugehen ist, da der Computer noch nichts gelernt hat), so wird sich der Algorithmus den Spielverlauf merken und beim nächsten Mal nicht mehr die gleichen Züge durchführen, da sie nicht gewinnbringend waren. Bei einem Sieg des Computers wird der Spielverlauf ebenso gespeichert und die Züge in Zukunft bevorzugt ausgeführt. Jederzeit gilt, dass bei einer unbekannten Spielsituation wieder der Zufallsgenerator den nächsten Zug bestimmt, solange bis wieder bekannte Situationen auftauchen.

Ziele

Durch eine Analyse der Anforderungen sollen Klassen identifiziert werden, um die Möglichkeit der objektorientierten Programmierung in Matlab zu nützen. Das System soll dabei so gestaltet werden, dass eine bestimmte Klasse für die Speicherung der Daten verantwortlich ist und nichts vom dahinter liegenden Spiel weiß. Somit ist es möglich das Programm durch eine neue Klasse des Typs Spiel sofort auf ein anderes Spiel zu erweitern. Die Grundidee bleibt dabei dieselbe, so dass wieder nur eine Gewinnabfrage definiert wird und keine Strategie zur Erreichung des Siegs. Diese ergibt sich automatisch aus den gelernten Daten.

Durch eine allgemein gehaltene Spieler-Klasse soll es möglich sein, dass zwei menschliche Spieler gegeneinander spielen bzw. der Mensch gegen den Computer. Die wichtigste Funktion des Programms wird allerdings die Möglichkeit des selbstständigen Lernens sein, so dass zwei Computer in hohem Tempo gegeneinander spielen können und eine immer größer werdende Lerndatenbank aufbauen. Damit sollte es nach einer bestimmten Zeit dieses Lernvorgangs nicht mehr möglich sein, gegen den Computer zu gewinnen. Die objektorientierte Programmierung wird im späteren Punkt zur Realisierungsphase noch genauer erklärt.

Weiters soll eine grafische Benutzeroberfläche erzeugt werden, die mit den dahinter liegenden Klassen interagiert. Dabei sollen die Namen der Spieler, der Schwierigkeitsgrad des Computers und die Art des Spiels ausgewählt werden können und die Spielfelder grafisch dargestellt werden.

Realisierungsphase

Analyse

Klassendiagramm

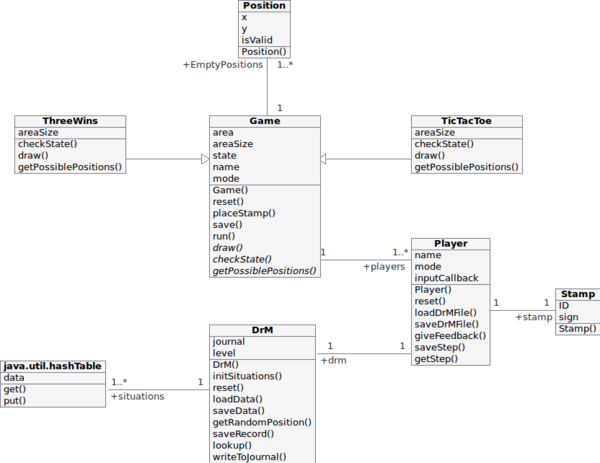
Die Analyse der Anforderungen ergab folgendes vereinfachtes Klassendiagramm.

Klassendiagramm des Projekts

Erklärung der Klassen

• Game

  Hier handelt es sich um eine abstrakte Klasse, die Attribute und Methoden vorgibt, welche eine abgeleitete Klassen besitzen muss, um mit dem Programm verwendet werden zu können. Die drei kursiven Methoden sind die einzigen Methoden, die von einer vererbten Klasse implementiert werden müssen, da sich diese von Spiel zu Spiel unterscheiden.

• TicTacToe

  Abgeleitet von Game. Die Methode getPossiblePositions() gibt alle leeren Felder zurück auf die noch gesetzt werden kann. checkState() überprüft, ob einer Spieler gewonnen hat oder ob ein Unentschieden erspielt wurde. draw() ist eine Methode, die das Spielfeld auf der Konsole ausgibt und wird in späterer Folge durch die GUI ersetzt.

• ThreeWins

  Abgeleitet von Game. Die Methode getPossiblePositions() überprüft welche Spalten noch nicht mit vier Steinen voll sind und gibt die restlichen möglichen Spalten zurück. checkState() überprüft in allen Reihen, Spalten und Diagonalen, ob es einem Spieler gelungen ist drei Steine gleicher Farbe in Folge gesetzt zu haben.

• Player

  Diese Klasse kann sowohl einen menschlichen als auch einen computerbasierten Gegner repräsentieren. Die Klasse Game besitzt ein Feld von Spielern und interagiert über die Methode getStep() mit diesen. Dabei macht es für die Klasse Game keinen Unterschied ob die Koordinaten von getStep() per Benutzerinteraktion eingegeben wurden oder im Falle eines künstlichen Gegners berechnet wurden. Dies ist hier der große Vorteil der objektorientierten Programmierung. Über die Methode giveFeedback() teilt die Klasse Game dem Spieler mit, ob das vorherige Spiel gewonnen oder verloren wurde, was im Falle eines künstlichen Gegners weiter verarbeitet wird.

• DrM

  Die zentralste Klasse dieses Projekts. Diese Klasse verwaltet die gesamten Lerndaten, berechnet Gewinn- und Verlustwahrscheinlichkeiten und kann bei vorgegebenen Spielsituationen den optimalsten nächsten Schritt zurückliefern. Um dem Spielecomputer eine gewisse Persönlichkeit zu verleihen wird er nachfolgend Dr. M. genannt, woraus sich auch der Klassenname herleitet. Fordert das laufende Spiel in der Methode run() der Klasse Game einen nächsten Spielzug über die Methode getStep() der Klasse Player an, so wird im Falle eines Computergegners die Methode lookup() der Klasse DrM aufgerufen.

• java.util.hashTable

  Eine vordefinierte Java-Klasse, die das Speichern der Daten in sogenannten Hashtables ermöglicht.

Aktivitätsdiagram

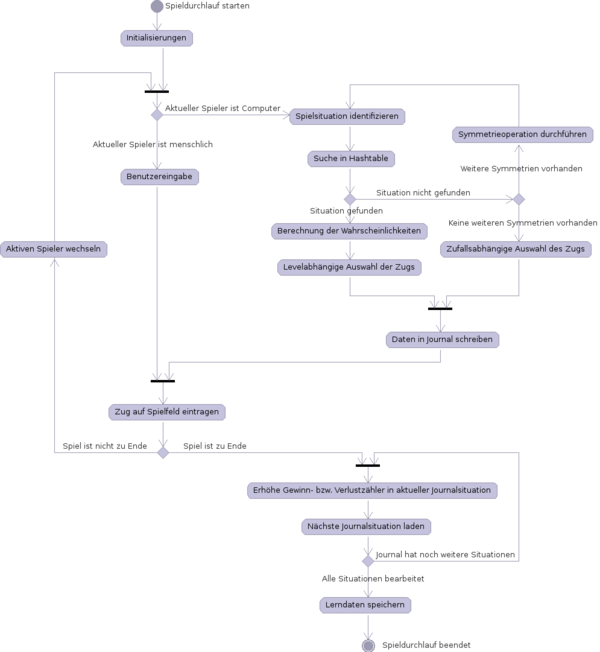
Der Ablauf eines Spiels kann am besten anhand eines groben Aktivitätsdiagramms dargestellt werden.

Aktivitätsdiagramm eines Spielablaufs

Erklärung des Algorithmus

Wird ein Spielzug des Computers angefordert, so wird eine eindeutige ID des aktuellen Spielfeldes erzeugt. Durch die Verwendung von java.util.Hashtables kann mit der Methode get() eine schnellere Suche als über die logische Indizierung durchgeführt werden. Wurde keine passende Situation gefunden, so wird im Fall von Drei gewinnt das Spielfeld vertikal gespiegelt und die Suche erneut durchgeführt. Bei der späteren Programmierung hat sich herausgestellt, dass es besser ist im schlechtesten Fall zweimal zu Suchen, als gleichbedeutende (symmetrische) Situationen doppelt zu speichern, da während der Lernphasen oft Arbeitsspeicher im 500 Megabyte Bereich angefordert werden mussten.

Jeder Hashtable-Eintrag beinhaltet eine Matrix, in der die Zeilen die verschiedenen möglichen Spielzüge auf diese Spielsituation repräsentieren. In den Spalten stehen die jeweiligen Anzahlen von Siegen und Niederlagen, die mit diesem Spielzug erzielt wurden. Durch Berechnung der Gewinn/Remis/Niederlagen-Verhältnisse können Wahrscheinlichkeiten für diese Fälle berechnet werden. Der Spielzug mit dem minimalen Verlustrisiko ist der optimale Spielzug um Fortzufahren. In der Präsentation wird erläutert warum der Spielzug mit der höchsten Gewinnwahrscheinlichkeit nicht optimal ist.

Bei Unkenntnis einer Spielsituation wird per Zufallsgenerator ein Zug erzeugt.

Der durchgeführte Spielzug (egal ob berechnet oder per Zufall) wird zusammen mit der ID der Spielsituation in einem Journal abgespeichert. Nachdem das Spiel beendet wurde, wird das Spielerobjekt über Sieg oder Niederlage informiert. Dann wird das Journal durchlaufen und die jeweiligen Gewinn- bzw. Niederlagenzähler erhöht.

Dadurch hat der Computer wieder eine Lerninformation mehr erhalten und der nächste Spieldurchlauf mit den aktualisierten Lerndaten beginnt wieder von vorne.

Design

GUI- Präsentation der Bedienerführung

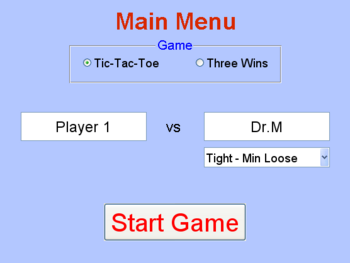
Bei Start des Programs im Spielbetrieb öffnet sich zuerst eine Oberfläche, welche es ermöglicht die Basiseinstellungen für das Spiel vorzunehmen.
Über die Auswahl mittels Radiobutton kann man die gewünschte Spielart einstellen. Außerdem ist es möglich im Textfeld mit der Inschrift PLAYER 1 den eigenen Namen einzutragen. Es stehen weiters 4 Spielmodi zur Verfügung, wobei man zwischen drei unterschiedlich agierenden Computergegnern auswählen oder gegen einen menschlichen Mitspieler antreten kann. Entscheidet man sich für einen menschlichen Gegner, so kann auch dieser seinen Namen ins vorgesehene Textfeld eingeben.

Startansicht der GUI.

Mögliche Basiseinstellungen.

Nach Drücken des Startbuttons verschwindet die Startoberfläche und die jeweilige Spieloberfläche erscheint.

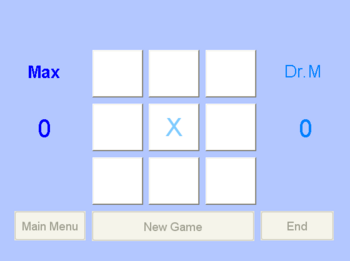
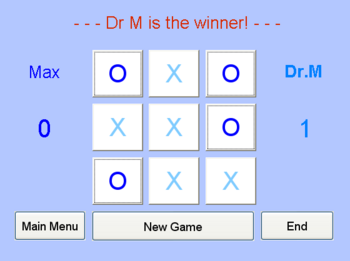
Hat der Spieler TicTacToe ausgewählt, erscheint die typische 3x3 Spieloberfläche. Durch einen Klick auf das entsprechende Feld wird eine Marke gesetzt. Ist das Spiel beendet, sei es durch den vorzeitigen Gewinn eines Spielers oder durch ein Unentschieden, so wird das Ergebnis bekanntgegeben und die jeweiligen Spielstände werden angepasst.
Nach dem Spiel ist es mittels der drei unten liegenden Buttons möglich, das Spiel eine weitere Runde lang zu spielen, wobei die Spielstände selbstverständlich mitgenommen werden (New Game), zu den Basiseinstellungen zurückzukehren (Main Menu), oder das Spiel zu beenden (End). Aus Stabilitätsgründen werden diese Buttons während eines Spiels deaktiviert.

Startansicht der Spieloberfläche von TicTacToe. Der Computer hat bereits gesetzt.

Ansicht der Spieloberfläche von TicTacToe nach Beendigung des Spiels. Der Gewinner wird angezeigt, die Zähler werden aktualisiert.

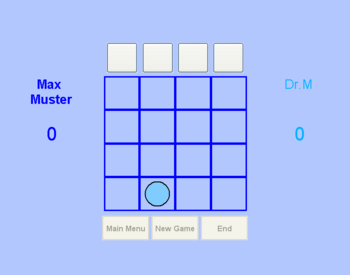
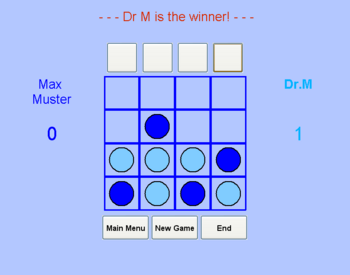
Bei Auswahl des Spiels Drei gewinnt erscheint eine 4x4 Oberfläche. Das Setzen der Spielsteine erfolgt hier durch Klicken auf einen der oberen vier Buttons, wobei jeder Button einer Spalte zugeordnet ist. Wenn eine Spalte gefüllt ist, so wir der zugehörige Button deaktiviert um einen "Überlauf" zu verhindern.
Für die weiteren Möglichkeiten nach Beendigung des Spiels gilt Gleiches wie schon bei TicTacToe beschrieben.

Startansicht der Spieloberfläche von Drei gewinnt.

Ansicht der Spieloberfläche Drei gewinnt nach Beendigung des Spiels. Der Gewinner wird angezeigt, die Zähler werden aktualisiert.

Programmierung des GUI

Um dem Benutzer die Bedienung zu erleichtern, wurde die Implementierung eines GUI beschlossen. Dies führte zu vereinzelten Schwierigkeiten, da die Verwendung des GUI für den Betrieb eines Spieles eine gewisse Zweckentfremdung der Funktion darstellt.
Das oben beschriebene Fenster Main Menu stellt die klassische Anwendung eines GUI in Matlab dar. Es können gewisse Einstellungen vorgenommen werden, die in der Handle Struktur des GUI in der Zuweisung einiger Variablen umgesetzt werden. Das Drücken des Startbuttons führt zum Aufruf einer Callbackfunktion. In unserem Fall wird in dieser Funktion wiederum eine Funktion zum Start des Spieles aufgerufen, wobei alle durch die Einstellungen festgelegten Variablen zum Funktionsaufruf verwendet werden.

Schwieriger liegen die Dinge bei den jeweiligen Spieloberflächen. Hier wird nämlich nicht nur einmal eine Funktion aufgerufen, sondern das GUI muss während des Spiels immer wieder aktualisiert werden. Dabei liegt dem GUI eine eigene Handle Struktur zugrunde, welche im aktuellen Workspace nicht zur Verfügung steht. Die jeweiligen Funktionen müssen deshalb die gesamte Handle Struktur aus dem GUI laden, die entsprechenden Änderungen vornehmen und die Struktur dann wieder rückspeichern.
Besonders schwierig gestaltet sich dieser Umstand beispielsweise bei der Aktualisierung des Plots von Drei gewinnt. Hier muss der axes Handle, bestehend aus einer Zahl die die Position des Plotfensters im Speicher identifiziert, aktualisiert werden. Die Übergabe dieser Zahl war schlussendlich nur durch Festlegung einer globalen Variablen zu bewerkstelligen.

Außerdem ist zu beachten, dass alle in der Struktur eines GUIs abgespeicherten Daten verloren gehen, sobald das GUI geschlossen wird. Besonders wenn man wie in unserem Fall mit zwei GUIs arbeitet sollte man dies beachten, denn oft benötigt man die im Fenster Main Menu abgefragten Daten auch in der Spieloberfläche (beispielsweise den Spielernamen). Durch die Objektorientiertheit des zugrundeliegenden Algorithmus können diese Daten aber nicht in Form einer Variablen in einem Skript gespeichert werden sondern müssten durch alle Funktionen gezogen werden. Deshalb empfiehlt es sich das Fenster bei Nichtbenutzung nicht zu schließen sondern nur unsichtbar zu machen um so die zugrundeliegende Struktur zu erhalten.
Grundsätzlich sind alle Interaktionen des GUI mit den dem Spiel zugrundeliegenden Funktionen und Klassen möglich, doch erfordert die Aktualisierung der Oberfläche in "Echtzeit" einiges an zusätzlichem Aufwand.

Resultate

Ermittlung der Lerndaten

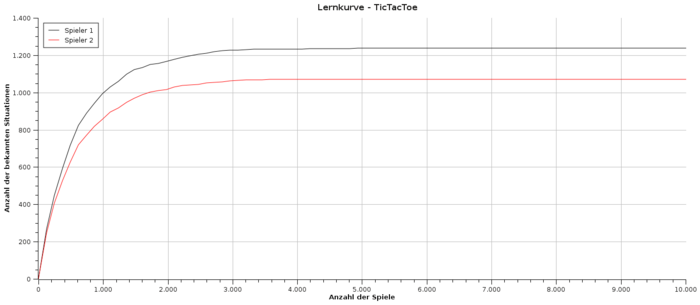
Wie bereits erwähnt können Lerndaten erzeugt werden, indem zwei Computergegner gegeneinander spielen. Hier war es wichtig das Programm sehr performanceorientiert zu implementieren, um möglichst viele Spiele pro Minute berechnen zu können. Eine interessante Grafik ergibt sich, wenn die Anzahl der insgesamt bekannten Spielsituationen über der Anzahl der gespielten Spiele dargestellt wird. Dabei ist zu beachten, dass der beginnende Computergegner mehr verschiedene Situationen kennenlernen wird, da er zu Beginn ein leeres Spielfeld vorfindet und der zweite Spieler jeweils eine Möglichkeit weniger für den ersten Zug hat.

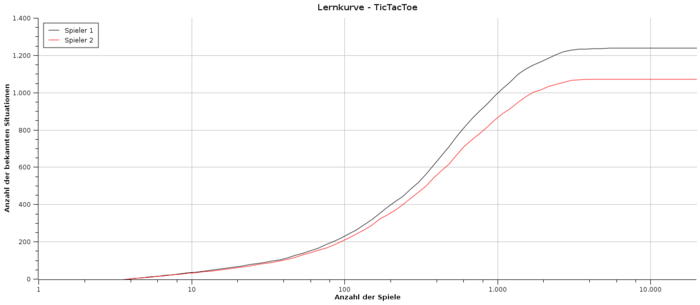
TicTacToe

Die folgenden Abbildungen zeigen, dass nach etwa 4.000 Spielen keine neuen Situationen mehr kennengelernt werden. Das bedeutet jedoch noch nicht, dass der Computer perfekt spielen wird, da er jede Situation öfter als nur einmal spielen muss, um genaue Wahrscheinlichkeiten für Sieg bzw. Niederlage berechnen zu können. Dabei gilt, je öfter eine Situation gespielt wurde, desto eher wird der Wert für die jeweilige Wahrscheinlichkeit konvergieren und desto besser wird der Computer schlussendlich spielen.

Lernkurve von TicTacToe in linearer Darstellung

Lernkurve von TicTacToe in logarithmischer Darstellung

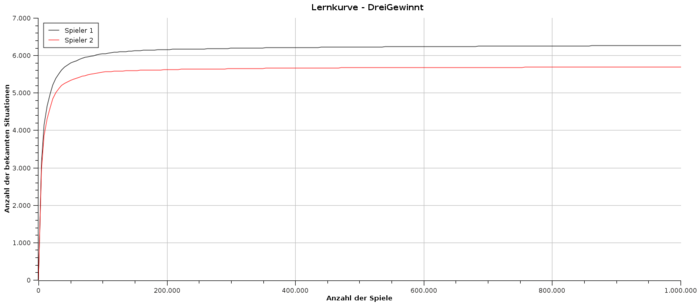
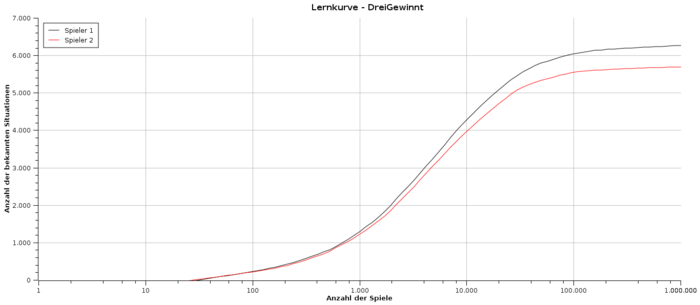
Drei gewinnt

Obwohl das Spielfeld um nur eine Zeile und eine Spalte vergrößert wurde, bedeutete dies einen unglaublichen Anstieg der möglichen Situationen. Auch wenn die folgenden Abbildungen ähnlich aussehen wie jene von TicTacToe, so ist das Hauptaugenmerk auf die Skalierung der x-Achse zu legen. In der logarithmischen Darstellung ist deutlich zu erkennen, dass nach 1.000.000 Durchläufen zwar fast, aber noch nicht ganz Konvergenz erreicht wurde. Da hier wieder gilt, dass selbst nach Kennenlernen jeder Situation noch weitergespielt werden sollte, bedeutet das weitere mehrere Stunden Rechenzeit. Bei der Anzahl der Situationen auf der y-Achse ist zu beachten, dass die Symmetrie um die vertikale Achse berücksichtigt wurde.

Lernkurve von Drei gewinnt in linearer Darstellung

Lernkurve von Drei gewinnt in logarithmischer Darstellung

Resümee

Es zeigte sich bald, dass die größte Hürde in den großen Datenmengen liegt, welche bei dieser Art der Programmierung auftreten. Dies kann man sich leicht veranschaulichen wenn man bedenkt, dass während der Lernphase in jeder Spielsituation überprüft werden muss, ob diese Situation nun schon einmal aufgetreten ist oder ob es sich um eine gänzlich neue Situation handelt. Natürlich müssen hierfür jedesmal alle bereits abgespeicherten Situationen mit der gerade vorherrschenden verglichen werden.

Im Falle des Spiels Tic-Tac-Toe stellten diese Fakten noch kein nennenswertes Problem dar, da es hier nur 255.168 verschiedene Spielverläufe gibt [1]. Dies stellt für einen modernen Rechner keine große Hürde dar und ist sogar ohne aufwändige Optimierungen programmierbar. Anders sieht es hier schon beim Spiel Vier gewinnt aus, bei dem es immerhin 7.1*10^13 verschiedene mögliche Bilder gibt [2]. Selbst unter Zuhilfenahme der hier einzig sinnvollen Symmetrieoperation (Spiegelung an der vertikalen Mittelachse) lässt sich diese Zahl nur halbieren, was immer noch 3.55*10^13 verschiedene Möglichkeiten bedeutet. Nun lässt sich diese Zahl an Spielsituationen bei heutigen Speicherdichten immer noch mit herkömmlichen Rechnern abspeichern, doch während dem Lernprozesses müssen wie bereits oben erwähnt immer alle bereits bekannten Situationen überprüft werden, um eine neue Situation erkennen zu können. Was dies schon bei Durchgang 1*10^10 bedeutet wird dem Leser sofort klar sein.

Da nun das Verwenden eines Clusters für dieses Projekt gleichermaßen übertrieben wie das zweiwöchig durchgängige Rechnen mit dem Privatrechner für dessen temperaturempfindliche Teile schädlich ist, wurde beschlossen stattdessen eine kleine Version eines Drei gewinnt auf einem 4*4 Spielfeld zu realisieren.

Durch die bereits vorigen Abschnitt beschriebenen Optimierungsmaßnahmen war die Durchführung dieses Projektes nun möglich. Dies zeigt, dass mit dem gewählten Ansatz auch das Spiel Vier gewinnt programmiert werden könnte, wenn man im Lernprozess über die erforderliche Rechenleistung verfügt. Eine weitere Verkomplizierung, zum Beispiel durch die dreidimensionale Form des Spieles (Sogo), würde dann wahrscheinlich auch im Spielverlauf zu Verzögerungen führen.

Literaturverzeichnis

[1]: http://de.wikipedia.org/wiki/Tic_Tac_Toe
[2]: Victor Allis Master's Thesis mit der Lösungsstrategie (PDF - Datei) in: 1988 as Report IR-163 by the Faculty of Mathematics and Computer Science at the Vrije Universiteit Amsterdam, The Netherlands. Also published in 1992 as Report CS 92-04 by the Faculty of General Sciences at the University of Limburg, Maastricht, The Netherlands. (http://www.connectfour.net/Files/connect4.pdf)