Simulation unseres Sonnensystems

Projektdefinition

Projektidee Die Idee, die hinter diesem Projekt steckt, ist eine Simulation unseres Sonnensystems. Im Vordergrund dieser Simulation steht die programmtechnische Verwirklichung der physikalischen Zusammenhänge und nicht die grafische Darstellung. Ziele Wirklichkeitsgetreue Simulation unseres Sonnensystems Leichte Adaptierbarkeit auf ein beliebiges Sonnensystem Programmtechnische Anforderungen Kernfunktionalität ist die Modulation der physikalischen Beziehungen Lösung des Differentialgleichungssystems der Umlaufbahnen der Planeten Grafische Darstellung wahlweise in 2D oder 3D

Projektentwurf

Physikalische Grundlagen

Damit die Planetenumlaufbahnen berechnet werden können, muss folgendes Differentialgleichungssystem gelöst werden.

Anfangsbedingungen

• Startposition von n Planeten ([math]\vec r_1,\;\vec r_2,\;\cdots\;\vec r_n[/math])
• Startgeschwindigkeiten von n Planeten ([math]\vec v_1,\;\vec v_2,\;\cdots\;\vec v_n[/math])

Die Anfangsbedingungen wurden mit Hilfe von Wikipedia und der Astronomiesoftware Easysky eruiert. Simulationsstart ist am 2000-01-01 um 00:00 CMT.
Die Ungenauigkeit der Angaben von Easysky bzgl. der Startpositionen liegt bei [math]\approx 10^{-4}\;\%\;[/math]. Die Startgeschwindigkeiten haben eine Genauigkeit von [math]\approx 99.9\;\%\;[/math]. Da es in nicht kommerziellen Programmen zumeist nicht möglich ist die Geschwindigkeitsvektoren als Ausgabedaten zu erhalten, wird in der Simulation der Startgeschwindigkeitsvektor angenähert, indem zwei Positionen eines Planeten im zeitlichen Abstand von fünf Stunden ausgewertet werden. Die Subtraktion der beiden Positionsvektoren ergibt die Richtung der Startgeschwindigkeiten.

Differentialgleichungen

Geschwindigkeiten
[math]\vec \dot{r_1}\;=\;\vec v_1[/math]
[math]\vec \dot{r_2}\;=\;\vec v_2[/math]
[math]\cdots\;[/math]
[math]\vec \dot{r_n}\;=\;\vec v_n[/math]

Beschleunigungen
[math]\vec \dot{v_1}\;=\;\vec a_1[/math]
[math]\vec \dot{v_2}\;=\;\vec a_2[/math]
[math]\cdots\;[/math]
[math]\vec \dot{v_n}\;=\;\vec a_n[/math]

Die Teilbeschleunigungen, die ein Planet durch die Gravitationsfelder aller anderen Planeten erfährt, werden mit Hilfe des NEWTONschen Gravitationsgesetzes, das die Anziehungskraft zweier Massepunkte bzw. zweier homogener Kugeln, wie es Planeten in diesem Modell näherungsweise sind, berechnet:

[math]\vec F_n\;=\;-\gamma\;\frac{m_nm_2}{r^2}\frac{\vec r}{\begin{Vmatrix} r \end{Vmatrix}} [/math]    und    [math]\vec F_n\;=\;m_n\vec a_n [/math] [math]\Longrightarrow \vec a_n\;=\;-\gamma\;\frac{m_2}{r^2}\frac{\vec r}{\begin{Vmatrix} r \end{Vmatrix}} [/math]

[math]\vec F_n\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Gravitationskraft, die auf Planeten }n\mbox{ wirkt}\;[/math]
[math]m_n\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Masse des Planeten }n\;[/math]
[math]m_2\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Masse des weiteren Planeten zu dem die Gravitationskraft gerichtet ist}\;[/math]
[math]r\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Abstand der beiden Planeten}\;[/math]
[math]\vec a_n\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Gravitationsbeschleunigung des Planeten }n\;[/math]
[math]\gamma\;=\;6.67\;10^{-11}\;[/math]	[math]\cdots\;[/math]	[math]\mbox{Gravitationskonstante}\;[/math]

Um zur Gesamtbeschleunigung zu gelangen, werden alle Teilbeschleunigungen vektoriell addiert: [math]\vec a_{ges}\;=\;\vec a_1\;+\;\vec a_2\;+\;\cdots\;+\;\vec a_n[/math]

Sequenzdiagramm nach UML

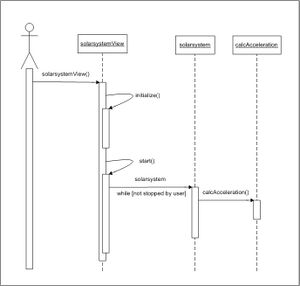
Das Sequenzdiagramm zeigt schematisch den Ablauf des Systems. Grundsätzlich ist das Sequenzdiagramm der objektorientierten Programmierung vorbehalten, doch auch in der strukturierten Programmierung kann man dadurch ausgezeichnete Einblicke in das System erlangen. Das Sequenzdiagramm beschreibt in der Horizontalen die Funktionen, die aufgerufen werden, die Vertikale repräsentiert die Zeit.

Sequenzdiagramm

Projektrealisierung

Die Lösung des Differentialgleichungssystem wird mit Hilfe des Solvers ode23 durchgeführt, da dieser geringere Toleranzwerte besitzt als ode45.
Die Zeit, die in der Simulation zwischen zwei dargestellten Frames vergeht, beträgt [math]\approx\,10^6\,[/math] Sekunden ([math]\approx\,11,5[/math] Tage). Außerdem ist es möglich das System auf eine beliebige Anzahl von Planeten zu erweitern oder zu reduzieren, in dem man die Konfigurationsdatei überarbeitet.
Die Darstellelung kann entweder in drei oder in zwei Dimensionen erfolgen.

Ergebnisse

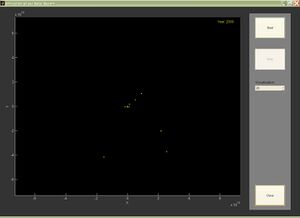
In nebenstehender Abbildung ist das Ergebnis der Simulation in 2D zu sehen. Die Sonne hat den Startpunkt [math](x\,=\,0,\,y\,=\,0,\,z\,=\,0)[/math]. Jedoch behält sie diesen über längere Zeit gesehen nicht exakt bei, da sie auch von den anderen Planeten - wenn auch auf Grund der weit größeren Masse nicht gravierend - angezogen wird. Bezüglich der Stabilität und der Übereinstimmung der Simulation mit der Wirklichkeit kann ausgesagt werden, dass die Planetenbahnen stabil sind, dh es treten keine Planeten aus ihren Umlaufbahnen aus. Diese Ausage beruht auf einen Test, der bis zum Jahr 15.000 erfolgreich durchgeführt wurde. Jedoch sollte hier auf die Ungenauigkeiten der Initialisierungsdaten hingewiesen werden (siehe auch Anfangsbedingungen).

Start der Simulation am 2000-01-01

Kontakt

Für Fragen oder Anregungen stehe ich gerne zur Verfügung (knami)