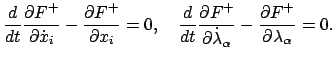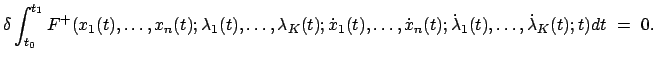Unterabschnitte
Anhang über Variationsrechnung
In diesem Anhang werden die Problemstellung und die Lösungsmethoden der
Variationsrechnung kurz erläutert und mit denen der gewöhnlichen
Maximum-Minimum-Rechnung verglichen.
Maximum-Minimum-Rechnung
Gegeben ist eine Funktion
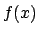 gegeben.
|
Variationsrechnung
Gegeben ist ein bestimmtes Integral
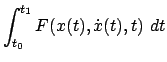 gegeben,
worin
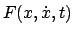 als Funktion seiner Argumente als Funktion seiner Argumente
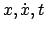 bekannt ist. bekannt ist.
|
Gesucht ist ein Wert 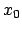 , für den , für den 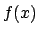 einen Extremwert annimmt. einen Extremwert annimmt.
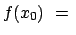 Extr.
|
Gesucht ist eine Funktion 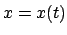 , die in das obige Integral eingesetzt,
diesem einen extremen Wert verleiht: , die in das obige Integral eingesetzt,
diesem einen extremen Wert verleiht:
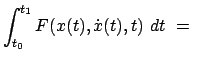 Extr. Extr. |
(121) |
|
Lösungsvorschift: Die Werte 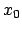 suchen,
für die die erste Ableitung der Funktion Null ist: suchen,
für die die erste Ableitung der Funktion Null ist:
|
Lösungsvorschift: Die erste Variation des Integrals muß Null sein:
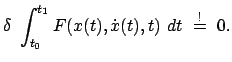 |
(122) |
|
Wie unten gezeigt wird, ist das der Fall, wenn die Funktion 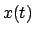 Lösung der
Eulerschen Differentialgleichung des Variationsproblems ist: Lösung der
Eulerschen Differentialgleichung des Variationsproblems ist:
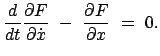 |
(123) |
|
Die Problemstellung der Variationsrechnung soll zunächst am Beispiel
der Brachystochrone (Abb. A.2(b)) erläutert werden: Ein Teilchen
bewegt sich in einer vertikalen Ebene auf einer vorgeschriebenen Kurve unter
dem Einfluß der Schwerkraft. Welche Kurve muß man wählen, damit die Laufzeit
vom gegebenen Anfangspunkt 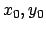 zum gegebenen Endpunkt
zum gegebenen Endpunkt 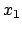 ,
, 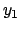 möglichst kurz ist?
möglichst kurz ist?
Dazu wird der Energiesatz für ein Teilchen der Masse
 im Schwerefeld nach der Geschwindigkeit aufgelöst
im Schwerefeld nach der Geschwindigkeit aufgelöst
Die Bahnkurve soll so gewählt werden, daß die Laufzeit 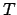 ein Extremum ist:
ein Extremum ist:
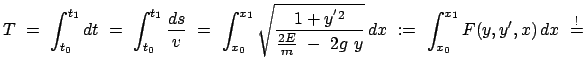 Extr. Extr. |
(124) |
Die Methode zur Lösung des Variationsproblems (A.1) besteht darin, daß das
Variationsproblem auf ein gewöhnliches Maximum-Minimum-Problem zurückgeführt
wird. Dazu wird angenommen, daß die Lösung 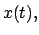 die dem Integral in
Gl. (A.1) einen extremalen Wert verleiht, schon bekannt ist. Der mit der
Lösung
die dem Integral in
Gl. (A.1) einen extremalen Wert verleiht, schon bekannt ist. Der mit der
Lösung 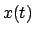 berechnete Wert des Integrals (A.1), nämlich
berechnete Wert des Integrals (A.1), nämlich
wird verglichen mit den Werten, die man erhält, wenn man in das Integral (A.1)
die folgenden Vergleichsfunktionen
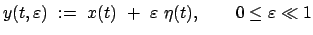 |
(125) |
einsetzt. Diese sollen in der Nähe von 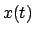 liegen
(daher
liegen
(daher
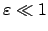 !) und
durch denselben Anfangs- und Endpunkt gehen wie die Lösung
(vgl. Abb. A.1), d.h.
!) und
durch denselben Anfangs- und Endpunkt gehen wie die Lösung
(vgl. Abb. A.1), d.h.
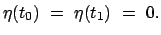 |
(126) |
Abbildung:
Die Lösung 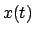 -- und
zwei Vergleichsfunktionen
-- und
zwei Vergleichsfunktionen
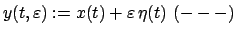 .
.
|
|
Einsetzen der Vergleichsfunktionen in das Integral (A.1) gibt:
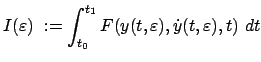 |
(127) |
Es ist klar, daß
 ist. Weil
ist. Weil 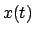 die Lösung des
Variationsproblems ist, also dem Integral (A.1) den extremalen Wert verleiht, muß
aber auch gelten:
die Lösung des
Variationsproblems ist, also dem Integral (A.1) den extremalen Wert verleiht, muß
aber auch gelten:
Durch diese Vorgangsweise mit dem Ansatz (A.5) und dessen Einsetzen in (A.1)
ist das Variationsproblem in ein
gewöhnliches Extremalproblem bezüglich des Parameters
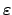 transformiert worden. Dies wird nun weiter im Integral (A.7) ausgeführt:
Für
transformiert worden. Dies wird nun weiter im Integral (A.7) ausgeführt:
Für
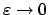 folgt daraus gemäß (A.4)
folgt daraus gemäß (A.4)
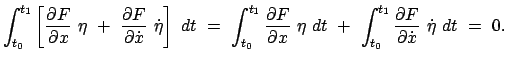 |
(128) |
Im zweiten Integral wird die Zeitableitung
durch partielle Integration überwälzt:
Wegen (A.5) ist der integrierte Anteil Null. Durch Einsetzen der gerade
berechneten Relation in das Integral (A.8) wird dieses auf folgende Form
gebracht:
Die Funktion 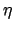 ist in hohem Maße willkürlich.
Deswegen kann das vorstehende Integral nur dann Null sein, wenn der Ausdruck
in der Klammer Null ist. Dies gibt die Eulersche Differentialgleichung
des Variationsproblems (A.1):
Deren Lösung
ist in hohem Maße willkürlich.
Deswegen kann das vorstehende Integral nur dann Null sein, wenn der Ausdruck
in der Klammer Null ist. Dies gibt die Eulersche Differentialgleichung
des Variationsproblems (A.1):
Deren Lösung 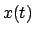 ist die gesuchte Funktion, die dem Integral (A.1) seinen extremalen
Wert verleiht.
ist die gesuchte Funktion, die dem Integral (A.1) seinen extremalen
Wert verleiht.
In dem wichtigen Spezialfall, daß die Funktion
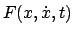 nicht
explizit von der unabhängigen Variablen
nicht
explizit von der unabhängigen Variablen  abhängt, ist folgende einfachere
Bedingung, das Jacobiintegral, der Eulerschen Differentialgleichung äquivalent:
abhängt, ist folgende einfachere
Bedingung, das Jacobiintegral, der Eulerschen Differentialgleichung äquivalent:
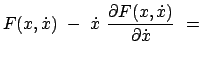 const. const. |
(129) |
Aus
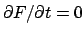 und aus Gl. (A.3) folgt nämlich
und aus Gl. (A.3) folgt nämlich
Diese Resultate werden nun zur Lösung des Beispiels, Gl. (A.4), verwendet. Zur
Anfangsbedingung
gehört 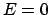 , sodaß wir schreiben können
, sodaß wir schreiben können
Es ist sehr langwierig, zu diesem Variationsproblem die Eulersche
Differentialgleichung (A.3) aufzustellen und zu lösen. Da 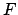 nicht
explizit von
nicht
explizit von 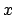 , der unabhängigen Variablen, abhängt, kann Formel
(A.9) verwendet werden, was wesentlich
günstiger ist. Diese lautet hier:
, der unabhängigen Variablen, abhängt, kann Formel
(A.9) verwendet werden, was wesentlich
günstiger ist. Diese lautet hier:
Diese Differentialgleichung kann durch Separation der Variablen gelöst werden
Das Integral wird mittels der nachfolgenden Substitution für 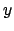 ausgewertet.
Damit folgt dann aus der obigen Gleichung auch ein Ausdruck für
ausgewertet.
Damit folgt dann aus der obigen Gleichung auch ein Ausdruck für 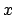 .
.
Diese Lösung ist eine Parameterdarstellung einer gewöhnlichen Zykloide
(s. Gl. (6.11)). Die noch unbestimmten Konstanten ( 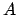 ,
, 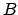 ,
,
 ,
, 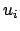 ) werden durch den vorgeschriebenen Anfangspunkt
) werden durch den vorgeschriebenen Anfangspunkt
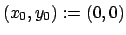 und Endpunkt
und Endpunkt
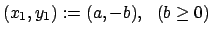 festgelegt.
festgelegt.  und
und 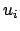 legen den Bereich des Parameters
legen den Bereich des Parameters 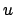 fest,
fest,
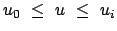 .
.
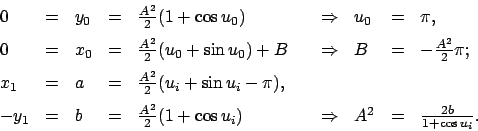 |
(1212) |
Division der vorletzten Gleichung durch die letzte gibt nach Umordnen
Diese Gleichung wird durch Einführung von Hilfsvariablen
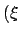 und
und 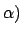 umgeformt.
umgeformt.
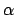 wird durch die obige Definition festgelegt. Die letzte Gleichung ist eine
transzendente Gleichung in
wird durch die obige Definition festgelegt. Die letzte Gleichung ist eine
transzendente Gleichung in 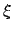 , das seinerseits das gesuchte
, das seinerseits das gesuchte 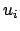 gibt. Die Lösungen
gibt. Die Lösungen
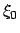 ,
, 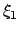 ,
, 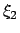 , ... sind die Schnittpunkte der Geraden
mit der Sinuskurve
, ... sind die Schnittpunkte der Geraden
mit der Sinuskurve
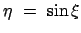 , (s. Abb. A.2):
gibt den Anfangspunkt. Die übrigen Wurzeln
(für
, (s. Abb. A.2):
gibt den Anfangspunkt. Die übrigen Wurzeln
(für
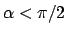 endlich viele)
geben zum Endpunkt passende Parametergrenzen
endlich viele)
geben zum Endpunkt passende Parametergrenzen
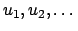 .
Aus
.
Aus 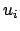 folgt dann
folgt dann
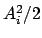 gemäß der letzten Gl. (A.12). Damit und mit (A.10),
(A.11) ist die Brachystrochrone (A.4) vollständig bestimmt.
gemäß der letzten Gl. (A.12). Damit und mit (A.10),
(A.11) ist die Brachystrochrone (A.4) vollständig bestimmt.
Aus Abb. A.2(a)) ersieht man: Für
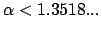 gibt es neben
gibt es neben 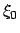 nur eine Wurzel
nur eine Wurzel 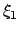 , (
, (
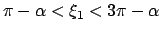 );
für 1.3518 ...
);
für 1.3518 ...
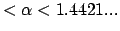 gibt es
gibt es 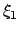 ,
, 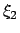 ,
, 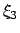 ,
(
,
(
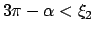 ,
,
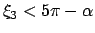 ). Die zu
). Die zu  ,
, 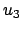 gehörigen Zykloiden (s. Abb. A.2(b)) haben längere Laufzeiten als die zu
gehörigen Zykloiden (s. Abb. A.2(b)) haben längere Laufzeiten als die zu
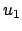 gehörige. Sie sind wegen der Reibung praktisch nicht realisierbar.
gehörige. Sie sind wegen der Reibung praktisch nicht realisierbar.
Abbildung:
Links: a) Die Lösungen
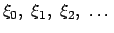 für einen
bestimmten Wert von
für einen
bestimmten Wert von 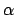 sind die Schnittpunkte der zu diesem
sind die Schnittpunkte der zu diesem 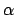 gehörigen Geraden mit
gehörigen Geraden mit 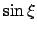 .
Rechts: b) Zu jedem Wert
.
Rechts: b) Zu jedem Wert
 gehört eine Brachystochrone.
gehört eine Brachystochrone.
![\includegraphics[width=16cm]{K11Bra}](img3446.gif) |
Die oben gebrachte Variationsrechnung läßt sich für den Fall von 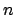 abhängigen Variablen
abhängigen Variablen 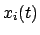 verallgemeinern: Gesucht sind die Funktionen
verallgemeinern: Gesucht sind die Funktionen
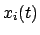 , sodaß das Integral
, sodaß das Integral
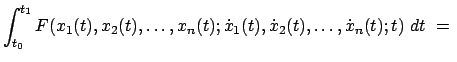 Extr. Extr. |
(1213) |
ein Extrem wird, wobei 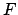 eine bekannte Funktion der Argumente ist.
Dies bedeutet also
Eine Schlußweise ganz wie die im Falle einer unbekannten abhängigen Variablen führt zu dem
System von Eulerschen Gleichungen
eine bekannte Funktion der Argumente ist.
Dies bedeutet also
Eine Schlußweise ganz wie die im Falle einer unbekannten abhängigen Variablen führt zu dem
System von Eulerschen Gleichungen
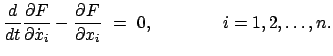 |
(1214) |
Es wird dazu angenommen, die 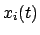 seien die gesuchten Funktionen, die
dem Integral seinen extremen Wert verleihen. Setzt man die Vergleichsfunktionen
seien die gesuchten Funktionen, die
dem Integral seinen extremen Wert verleihen. Setzt man die Vergleichsfunktionen
die durch den gleichen Anfangs- und Endpunkt gehen sollen wie die Lösungen, d.h.
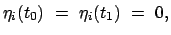 |
(1215) |
in das Integral (A.13) ein, dann ist das Variationsproblem wieder auf ein
gewöhnliches Extremalproblem für das folgende Integral zurückgeführt:
Die Ableitung des Integrals ist partiell integriert worden.
Der integrierte Term ist wegen Bedingung (A.15) Null. Wegen der Willkürlichkeit
und der Unabhängigkeit der 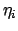 muß jede geschweifte Klammer für sich
Null sein. Das gibt die oben bereits angeführten Eulerschen
Gleichungen (A.14).
muß jede geschweifte Klammer für sich
Null sein. Das gibt die oben bereits angeführten Eulerschen
Gleichungen (A.14).
Als letztes behandeln wir Variationsprobleme mit Nebenbedingungen. In der
gewöhnlichen Maximum-Minimum-Rechnung sollen die Argumente
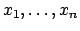 aufgesucht werden, die der Funktion
aufgesucht werden, die der Funktion
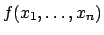 einen
extremen Wert verleihen. Dabei sind diese Argumente durch Nebenbedingungen
eingeschränkt.
einen
extremen Wert verleihen. Dabei sind diese Argumente durch Nebenbedingungen
eingeschränkt.
Die Lösungsvorschrift ist (ohne Beweis): Mittels Lagrangescher
Multiplikatoren
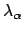 bilde man die Funktion
bilde man die Funktion
und suche deren Extrema gemäß
Der zweite Satz von Bedingungen sind gerade die Nebenbedingungen, die in
formaler Weise ebenfalls als Ableitungen ausgedrückt worden sind. Aus den obigen
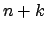 Gleichungen können die
Gleichungen können die 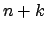 Unbekannten
Unbekannten
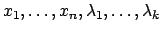 bestimmt werden.
bestimmt werden.
Das analoge Problem der Variationsrechnung ist wieder: die Funktionen 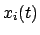 zu finden, so daß
zu finden, so daß
Diese Funktionen, 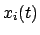 , werden durch die Nebenbedingungen
, werden durch die Nebenbedingungen
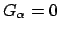 eingeschränkt. Kommen in den
eingeschränkt. Kommen in den
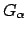 keine Ableitungen vor, heißen
die Nebenbedingungen holonom,
sonst anholonom. Die Lösungsvorschrift ist in beiden Fällen die
gleiche: Man bilde die Funktion
keine Ableitungen vor, heißen
die Nebenbedingungen holonom,
sonst anholonom. Die Lösungsvorschrift ist in beiden Fällen die
gleiche: Man bilde die Funktion
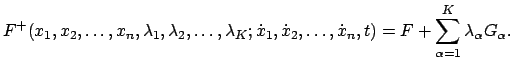 |
(1218) |
Die gesuchten Funktionen 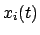 und die Lagrangeschen Multiplikatoren
und die Lagrangeschen Multiplikatoren
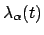 sind die Lösungen der Eulerschen
Differentialgleichungen
Daher kann man das Variationsproblem (A.16) und
(A.17) auch schreiben als
sind die Lösungen der Eulerschen
Differentialgleichungen
Daher kann man das Variationsproblem (A.16) und
(A.17) auch schreiben als
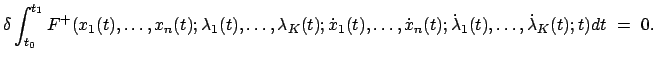 |
(1219) |
Die strenge mathematische Behandlung der Variationsrechnung ist ungleich
schwieriger als die der gewöhnlichen Maximum-Minimum-Rechnung. Insbesondere
ist die
Existenz von stationären Werten der Integrale (dieser Begriff ist allgemeiner
und zutreffender als der des Extremums) nicht immer gesichert. Auch der Beweis
der Methode der Lagrangeschen Multiplikatoren ist sehr kompliziert. Auf diese
Schwierigkeiten kann hier nicht eingegangen werden.
Literatur zur Variationsrechnung
O. Bolza: Vorlesung über Variationsrechnung, B.G.Teubner, Leipzig,1909
Christian Sommer
2003-01-27
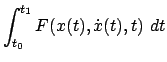 gegeben,
gegeben,
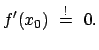
![]() zum gegebenen Endpunkt
zum gegebenen Endpunkt ![]() ,
, ![]() möglichst kurz ist?
möglichst kurz ist?
![]() im Schwerefeld nach der Geschwindigkeit aufgelöst
im Schwerefeld nach der Geschwindigkeit aufgelöst
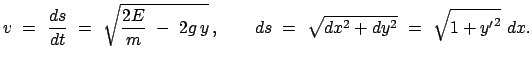
![]() die dem Integral in
Gl. (A.1) einen extremalen Wert verleiht, schon bekannt ist. Der mit der
Lösung
die dem Integral in
Gl. (A.1) einen extremalen Wert verleiht, schon bekannt ist. Der mit der
Lösung ![]() berechnete Wert des Integrals (A.1), nämlich
berechnete Wert des Integrals (A.1), nämlich
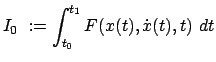
![]() ist. Weil
ist. Weil ![]() die Lösung des
Variationsproblems ist, also dem Integral (A.1) den extremalen Wert verleiht, muß
aber auch gelten:
die Lösung des
Variationsproblems ist, also dem Integral (A.1) den extremalen Wert verleiht, muß
aber auch gelten:
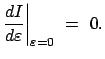
![$\displaystyle \frac{dI}{d \varepsilon} = \int_{t_{0}}^{t_{1}}
\left[ \frac...
...tial y} \eta + \
\frac{\partial F}{\partial \dot y} \dot \eta
\right] dt.
$](img3394.gif)
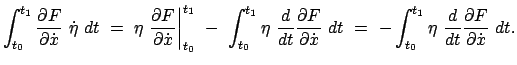
![$\displaystyle \frac{dI}{d \varepsilon} \bigg\vert _{\varepsilon = 0} = \
\in...
...al x} - \
\frac{d}{dt} \frac{\partial F}{\partial \dot x} \right] dt = 0.
$](img3398.gif)
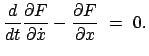
![]() nicht
explizit von der unabhängigen Variablen
nicht
explizit von der unabhängigen Variablen ![]() abhängt, ist folgende einfachere
Bedingung, das Jacobiintegral, der Eulerschen Differentialgleichung äquivalent:
abhängt, ist folgende einfachere
Bedingung, das Jacobiintegral, der Eulerschen Differentialgleichung äquivalent:
![$\displaystyle \frac{d}{dt} \left[ F(x,\dot{x}) - \dot{x} \frac{\partial F(x,\dot{x})
}{\partial \dot{x}}
\right] $](img3403.gif)
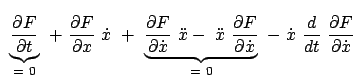
![$\displaystyle \dot{x} \left[ \frac{\partial F}{\partial x} - \frac{d}{dt}
\frac{\partial F}{\partial \dot{x}} \right]
= 0.$](img3405.gif)
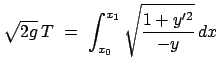
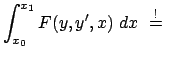 Extr.
Extr.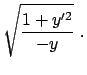
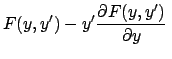
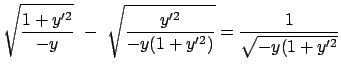
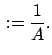
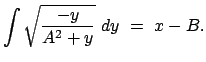
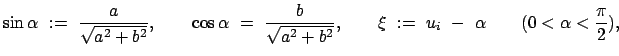
![]() gibt es neben
gibt es neben ![]() nur eine Wurzel
nur eine Wurzel ![]() , (
, (
![]() );
für 1.3518 ...
);
für 1.3518 ...
![]() gibt es
gibt es ![]() ,
, ![]() ,
, ![]() ,
(
,
(
![]() ,
,
![]() ). Die zu
). Die zu ![]() ,
, ![]() gehörigen Zykloiden (s. Abb. A.2(b)) haben längere Laufzeiten als die zu
gehörigen Zykloiden (s. Abb. A.2(b)) haben längere Laufzeiten als die zu
![]() gehörige. Sie sind wegen der Reibung praktisch nicht realisierbar.
gehörige. Sie sind wegen der Reibung praktisch nicht realisierbar.
![\includegraphics[width=16cm]{K11Bra}](img3446.gif)
![]() abhängigen Variablen
abhängigen Variablen ![]() verallgemeinern: Gesucht sind die Funktionen
verallgemeinern: Gesucht sind die Funktionen
![]() , sodaß das Integral
, sodaß das Integral
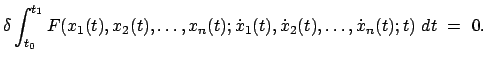
![]() seien die gesuchten Funktionen, die
dem Integral seinen extremen Wert verleihen. Setzt man die Vergleichsfunktionen
seien die gesuchten Funktionen, die
dem Integral seinen extremen Wert verleihen. Setzt man die Vergleichsfunktionen
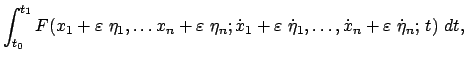
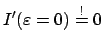
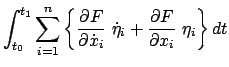
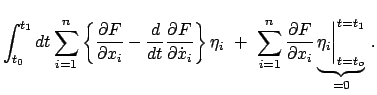
![]() muß jede geschweifte Klammer für sich
Null sein. Das gibt die oben bereits angeführten Eulerschen
Gleichungen (A.14).
muß jede geschweifte Klammer für sich
Null sein. Das gibt die oben bereits angeführten Eulerschen
Gleichungen (A.14).
![]() aufgesucht werden, die der Funktion
aufgesucht werden, die der Funktion
![]() einen
extremen Wert verleihen. Dabei sind diese Argumente durch Nebenbedingungen
eingeschränkt.
einen
extremen Wert verleihen. Dabei sind diese Argumente durch Nebenbedingungen
eingeschränkt.
![]() bilde man die Funktion
bilde man die Funktion
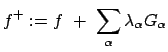
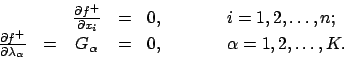
![]() zu finden, so daß
zu finden, so daß