Nächste Seite: Literatur Aufwärts: am_main Vorherige Seite: Anhang über Variationsrechnung Inhalt
In diesem Kapitel wird noch ein neuer Typ von Bewegungsgleichungen, die kanonischen Bewegungsgleichungen, abgeleitet werden. Diese eignen sich besonders zu allgemeinen Untersuchungen über die allgemeine Struktur der Mechanik. Die wichtigste Methode zur Lösung dieser Bewegungsgleichungen ist die der kanonischen Transformationen die es gestatten, mittels bekannter Integrale der Bewegung die Ordnung des Differentialgleichungssystems zu erniedrigen. Die Hamilton-Jacobische Theorie gibt ein allgemeines Verfahren zum Auffinden von solchen kanonischen Transformationen, die es im Prinzip gestatten, die Bewegungsgleichungen vollständig zu lösen.
Die Newtonschen Bewegungsgleichungen sind am Anfang in kartesischen Koordinaten
angegeben worden. Die Geometrie des Kraftfeldes oder das Bestehen von
Nebenbedingungen, die die Bewegungsfreiheit der Massenpunkte einschränken,
legen oft
die Verwendung von krummlinigen Koordinaten nahe. Diese Transformationen der
abhängigen Variablen
Ein weiterer Grund betrifft die Lösungsmöglichkeiten: Will man bekannte Integrale der Bewegung zur Lösung der Bewegungsgleichungen bzw. zur Verringerung deren Grades benützen, so reichen die Transformationen (12.1) nicht aus. Denn diese Integrale der Bewegung, wie z.B. Drehimpuls oder Gesamtenergie, hängen auch von den Geschwindigkeiten oder Impulsen ab. Transformationen für solche Größen müssen daher allgemeiner sein als die obigen Koordinatentransformationen (12.1). Diese allgemeineren Transformationen, die auch die Impulse erfassen, heißen kanonische oder Kontaktransformationen. Diese werden auf die kanonischen Bewegungsgleichungen angewendet.
Die kanonischen Bewegungsgleichungen werden aus dem Hamiltonschen Prinzip (Gl. (11.81))
Die Lagrangefunktion für ein konservatives mechanisches Problem bzw. für eines
mit verallgemeinertem Potential für ein geladenes Teilchen in einem
elektromagnetischen Feld ist
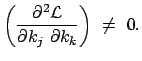
Dies ist die einfachste Form, die ein solches Variationsprinzip annehmen kann. Es treten nur die Ableitungen der einen Reihe von Variablen auf, auch diese nur linear. Die Eulerschen Gleichungen dieses Variationsprinzips
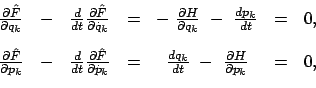
sind die Hamiltonschen oder kanonischen Bewegungsgleichungen:
Die vorhergehende Ableitung wird nochmals in Form eines Kochrezepts zusammengefaßt:
Aus der Lagrangefunktion
Die Größe (12.9) wird als kanonischer Impuls bezeichnet,
weil in einfachen Fällen, z.B. in
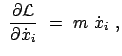 |
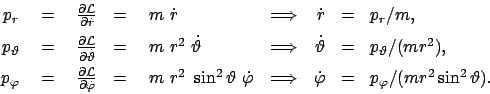
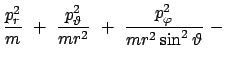 |
|||
![$\displaystyle - \frac{m}{2} \left[ \left( \frac{p_r}{m} \right)^2 + \
r^...
...\left( \frac{p_\varphi}{m r^2 \sin^2\vartheta} \right)^2 \right]
+ U(r) =$](img3517.gif) |
|||
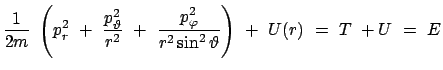 |

Mit ihrer Lösung werden wir uns erst später beschäftigen.
Wir betrachten eine Lagrangefunktion mit gewöhnlichem mechanischem Potential:
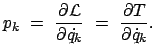
Die Lagrangefunktion für dieses Problem ist (s. Gl. 11.46)
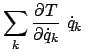 |
|||
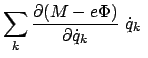 |
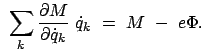 |
In kartesischen Koordinaten ist die Lagrangefunktion für ein Teilchen in einem elektromagnetischen Feld gegeben durch:
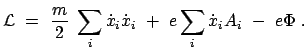
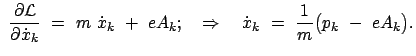 |
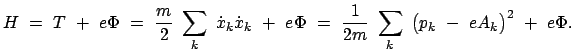
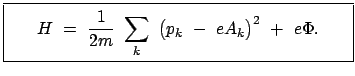 |
(1218) |
Eine Funktion mehrerer Variabler
![]() heißt eine
homogene Form, wenn sie nachfolgende Bedingung erfüllt:
heißt eine
homogene Form, wenn sie nachfolgende Bedingung erfüllt:
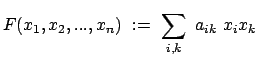
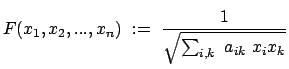
Der Satz von Euler lautet: Eine homogene Form vom Grade ![]() erfüllt
folgende Beziehung:
erfüllt
folgende Beziehung:
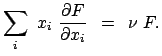 |
(1219) |
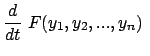 |
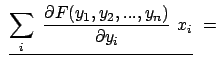 |
||
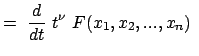 |
Der Phasenraum (E. phase space) ist der reelle ![]() -dimensionale Raum der
Koordinaten
-dimensionale Raum der
Koordinaten
![]() . In diesem entspricht der Bewegung eines Systems eine Raumkurve dargestellt
durch die
. In diesem entspricht der Bewegung eines Systems eine Raumkurve dargestellt
durch die ![]() Funktionen
Funktionen
Schreibt man die kanonischen Gleichungen (12.13) als Differenzengleichungen, so bekommt man:
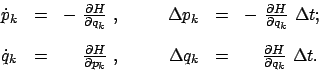
Der Phasenraum gestattet oft einen Überblick über die verschiedenen Typen von Bewegungen eines Systems. Er ist daher für viele dynamische Untersuchungen von Teilchenbewegungen in Beschleunigern, in der Astronautik und in der statistischen Mechanik sehr zweckmäßig. Die Tatsache, daß unsere Vorstellung auf den dreidimensionalen Raum beschränkt ist, ist ein Handikap (bei 2 Freiheitsgraden ist der Phasenraum bereits vierdimensional!). Doch genügen für viele Zwecke Projektionen des Phasenraums auf eine zweidimensionale Ebene. Diese Verwendung des Phsenraums soll an einigen Beispielen vorgeführt werden.
Aus der Lagrangefunktion erhält man den kanonischen Impuls. Damit bildet man die Hamiltonfunktion
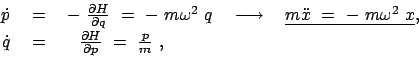 |
(1222) |
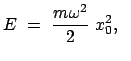 |
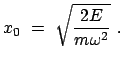 |
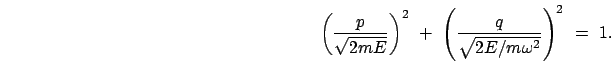
Diese ist in der ![]() -Ebene eine
Ellipse, auf der der den augenblicklichen Zustand des Systems beschreibende
Phasenpunkt während einer vollen Periode
-Ebene eine
Ellipse, auf der der den augenblicklichen Zustand des Systems beschreibende
Phasenpunkt während einer vollen Periode
![]() einmal herumläuft
(Abb. 12.1).
Jedem Energiewert
einmal herumläuft
(Abb. 12.1).
Jedem Energiewert ![]() entspricht eine mit den anderen konzentrische Ellipse mit den
Halbachsen
entspricht eine mit den anderen konzentrische Ellipse mit den
Halbachsen
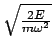 und
und
![]() .
Da in vielen Fällen nur die
Phasenbahn als ganzes, nicht aber der zeitliche Ablauf interessiert, ist es
nicht nötig, die Bewegungsgleichungen zu lösen; denn die Phasenkurve selbst
folgt bereits aus dem Energiesatz (12.21).
.
Da in vielen Fällen nur die
Phasenbahn als ganzes, nicht aber der zeitliche Ablauf interessiert, ist es
nicht nötig, die Bewegungsgleichungen zu lösen; denn die Phasenkurve selbst
folgt bereits aus dem Energiesatz (12.21).
Die Energie ist erhalten. Dies ist der Grund, daß die Phasenbahn nur einen
eindimensionalen Teilraum der zweidimensionalen Phasenebene, die eben erwähnte
Ellipse ausfüllt. Wäre die Energie nicht erhalten, sondern ginge sie ständig verloren,
dann würden die Halbachsen der Phasenellipse ständig schrumpfen. Die Phasenbahn würde
dann das Innere der zum Anfangswert ![]() gehörigen Ellipse spiralig ausfüllen.
gehörigen Ellipse spiralig ausfüllen.
Die kinetische Energie, die potentielle Energie (hier ist aber die z-Achse parallel
zur Erdbeschleunigung gerichtet, s. Abb. 12.2)
und die Lagrangefunktion sind unten angegeben. Daraus folgen der kanonische Impuls ![]() und die Hamiltonfunktion
und die Hamiltonfunktion ![]() . Die Lagekoordinate ist
. Die Lagekoordinate ist
![]() .
.
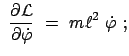 |
|||
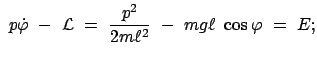 |
|||
Aus der Hamiltonfunktion (= der Gesamtenergie E) können die verschiedenen
Phasenbahnen gefunden werden. In der Tabelle sind diese aufgelistet
und in Abb. 12.2 eingezeichnet. ![]() ist der kleinstmögliche Energiewert;
das Pendel ist in Ruhe.
Diesem Zustand entspricht der Mittelpunkt des Diagramms (
ist der kleinstmögliche Energiewert;
das Pendel ist in Ruhe.
Diesem Zustand entspricht der Mittelpunkt des Diagramms (![]() ); er heißt
das Librationszentrum. Für
); er heißt
das Librationszentrum. Für
![]() schwingt das
Pendel. Die Phasenbahnen sind
geschlossene Kurven, die vom Phasepunkt in der angegebenen Richtung
durchlaufen werden. Dieser Bewegungstyp heißt Libration.
Für
schwingt das
Pendel. Die Phasenbahnen sind
geschlossene Kurven, die vom Phasepunkt in der angegebenen Richtung
durchlaufen werden. Dieser Bewegungstyp heißt Libration.
Für ![]() reicht der mögliche Variationsbereich der Lagekoordinate
reicht der mögliche Variationsbereich der Lagekoordinate ![]() von der Vertikalen (
von der Vertikalen (
![]() ) bis wieder zur Vertikalen. Die Schwingungsdauer
ist aber unendlich. Deswegen durchläuft der Phasenpunkt in
Abb. 12.2 nur einen Teil des oberen oder des unteren Asts der durch
) bis wieder zur Vertikalen. Die Schwingungsdauer
ist aber unendlich. Deswegen durchläuft der Phasenpunkt in
Abb. 12.2 nur einen Teil des oberen oder des unteren Asts der durch ![]() und
und ![]() gehenden Phasenbahn. Diese Limitationsbewegung trennt die Schwingungen von
den Rotationen des Pendels, die für
gehenden Phasenbahn. Diese Limitationsbewegung trennt die Schwingungen von
den Rotationen des Pendels, die für ![]() eintreten. Letzteren entsprechen
die wellenförmigen Kurven ausserhalb der Separatrix im Phasenraumdiagramm, Abb. 12.2.
Dieser Bewegungstyp heißt Nutation.
Vom Standpunkt der Schwingungen kann man die Librationsbewegung als stabil
betrachten, die Nutation als instabil. Die der Limitationsbewegung entsprechende
Phasenkurve trennt das stabile Gebiet vom instabilen und heißt daher die
Separatrix.
eintreten. Letzteren entsprechen
die wellenförmigen Kurven ausserhalb der Separatrix im Phasenraumdiagramm, Abb. 12.2.
Dieser Bewegungstyp heißt Nutation.
Vom Standpunkt der Schwingungen kann man die Librationsbewegung als stabil
betrachten, die Nutation als instabil. Die der Limitationsbewegung entsprechende
Phasenkurve trennt das stabile Gebiet vom instabilen und heißt daher die
Separatrix.
|
|
|
Ruhe | Librations- |
| -zentrum | |||
|
|
|
harmonische | Libration |
| Schwingung | |||
|
|
|
anharmonische | Libration |
| Schwingung | |||
|
|
|
Grenzfall | Limitations- |
| Separatrix | bewegung | ||
|
|
|
Rotation | Nutation |
Wir betrachten ein Teilchen im Feld einer anziehenden Zentralkraft. Wir
benützen Polarkoordinaten in der Bahnebene. Die zugehörige Hamiltonfunktion
findet man aus der für Kugelkoordinaten (Beispiel am Ende von §12.1) mittels
der Spezialisierung
![]() :
:
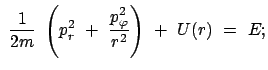 |
|||
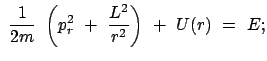 |
|||
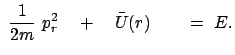 |
![\includegraphics[scale=0.83]{k12_zentr_kraft_pot}](img3616.gif) []
[]
![\includegraphics[scale=0.83]{k12_phasenraumproj_zentrpot}](img3617.gif) []
[]
![\includegraphics[scale=0.83]{k12_bahnkurve_zentrpot}](img3618.gif) |
Für
![]() ist die Bewegung auf einen Kreisring beschränkt, dessen
Grenzen
ist die Bewegung auf einen Kreisring beschränkt, dessen
Grenzen ![]() und
und ![]() aus dem obigen Ausdruck für die Gesamtenergie
für
aus dem obigen Ausdruck für die Gesamtenergie
für
![]() folgen.
folgen.
![]() entspricht ungebundener Bewegung
entspricht ungebundener Bewegung
![]() . Bei der Projektion
des vierdimensionalen Phasenraumes auf die
. Bei der Projektion
des vierdimensionalen Phasenraumes auf die ![]() -Ebene (Abb. 12.4) erhält man
geschlossene Kurven (Librationsbewegung) für
-Ebene (Abb. 12.4) erhält man
geschlossene Kurven (Librationsbewegung) für
![]() . Die Separatrix für
. Die Separatrix für
![]() erstreckt sich bis ins Unendliche, ebenso alle Phasenbahnen mit
erstreckt sich bis ins Unendliche, ebenso alle Phasenbahnen mit
![]() .
In der
.
In der ![]() -Ebene (Abb. 12.3(c)) sieht
man die wahre Bahn. Doch kann man diese nur für einen festen Energiewert
aufzeichnen. Außerdem erfordert dies die Lösung der
Bewegungsgleichungen. Dagegen kann man die Diagramme,
Abb. 12.3(a) und 12.3(b),
direkt aus dem Energiesatz ableiten und in ihnen für alle Energien die wesentlichen
Eigenschaften der Bahn einzeichnen.
-Ebene (Abb. 12.3(c)) sieht
man die wahre Bahn. Doch kann man diese nur für einen festen Energiewert
aufzeichnen. Außerdem erfordert dies die Lösung der
Bewegungsgleichungen. Dagegen kann man die Diagramme,
Abb. 12.3(a) und 12.3(b),
direkt aus dem Energiesatz ableiten und in ihnen für alle Energien die wesentlichen
Eigenschaften der Bahn einzeichnen.
Wichtige praktische Anwendungen derartiger Betrachtungen im Phasenraum liegen in der Astronautik. Ein Raumschiff, das vom Mond zur Erde zurückkehrt, darf nicht zu langsam und nicht zu flach auf den terrestrischen Luftmantel auftreffen, sonst wird es auf Niewiederkehr in den Weltraum reflektiert. Wenn es zu schnell oder zu steil auftrifft, wird die Luftreibung es mehr als zulässig erhitzen. Das sind im Phasenraum Bedingungen für minimale und maximale Geschwindigkeit und Auftreffwinkel, die ein ''Fenster'' vorschreiben, durch das die Phasenbahn des rückkehrenden Raumschiffes geführt werden muß.
| Phasenpunkte | Phasenbahnen | Dimension | |
|
|
1 | 1 | 2Nf |
|
|
N | N | 2f |
![\includegraphics[width=7.5cm]{K12A4}](img3630.gif) |
![\includegraphics[width=12.5cm]{K12PhPoi}](img3631.gif) |
Z.B. ein System von ![]() eindimensionlen Oszillatoren kann dargestellt
werden wie in Abb. 12.4. In Abb. 12.5(a) haben die Oszillatoren nahezu gleiche
Gesamtenergie
eindimensionlen Oszillatoren kann dargestellt
werden wie in Abb. 12.4. In Abb. 12.5(a) haben die Oszillatoren nahezu gleiche
Gesamtenergie ![]() , aber ihre momentanen Lagen sind über alle Möglichkeiten
statistisch verteilt. In Abb. 12.5(b) haben die Oszillatoren
nicht nur gleiche Energie, sondern sie schwingen auch nahezu kohärent
(Modell für Laser).
, aber ihre momentanen Lagen sind über alle Möglichkeiten
statistisch verteilt. In Abb. 12.5(b) haben die Oszillatoren
nicht nur gleiche Energie, sondern sie schwingen auch nahezu kohärent
(Modell für Laser).
Die statistische Mechanik benützt diese Beschreibung; sie liefert
gewissermaßen eine ''Hydromechanik der Flüssigkeit der Phasenpunkte'' im ![]() -Raum.
-Raum.
Wird nachgetragen !
Die Hamiltonfunktion eines Systems ist gleich dessen Gesamtenergie (vgl. §
12.1.1 und §12.1.2). Ist das System konservativ,
dann ist die Hamiltonfunktion zeitlich
konstant. Hängen das mechanische Potential ![]() (Gl. (12.5)) und das Potential des
elektromagnetischen Feldes
(Gl. (12.5)) und das Potential des
elektromagnetischen Feldes ![]() (Gl. (12.6)) nicht explizit von der Zeit ab, dann folgt
aus der Definition der Hamiltonfunktion, Gl. (12.11),
(Gl. (12.6)) nicht explizit von der Zeit ab, dann folgt
aus der Definition der Hamiltonfunktion, Gl. (12.11),
Die totale Zeitableitung der Hamiltonfunktion ist:
Tritt eine Variable, z.B. ![]() , die das System beschreibt, in der Lagrangefunktion
nicht auf, heißt sie zyklisch.
, die das System beschreibt, in der Lagrangefunktion
nicht auf, heißt sie zyklisch.
Aus der Lagrangeschen Gleichung 2. Art für ![]() , Gl. (11.38), und aus der Definition
des kanonischen Impulses, Gl. (12.9), folgt, daß der zur zyklischen
Variablen
, Gl. (11.38), und aus der Definition
des kanonischen Impulses, Gl. (12.9), folgt, daß der zur zyklischen
Variablen ![]() , konjugierte Impuls
, konjugierte Impuls ![]() , zeitlich konstant, also ein
Integral der Bewegung, ist:
, zeitlich konstant, also ein
Integral der Bewegung, ist:
Die verallgemeinerte Geschwindigkeit, ![]() , muß aber in der Lagrangefunktion
vorkommen, sonst ist die Variable
, muß aber in der Lagrangefunktion
vorkommen, sonst ist die Variable ![]() sinnlos. Aus der vorhergehenden Gleichung
folgt, daß
sinnlos. Aus der vorhergehenden Gleichung
folgt, daß ![]() auch in der Hamiltonfunktion nicht vorkommt:
auch in der Hamiltonfunktion nicht vorkommt:
Zusammenfassend: Jede zyklische Koordinate ist in der Hamiltonfunktion nicht enthalten, wohl aber ihr konjugierter Impuls. Dieser ist zeitlich konstant, ist ein Integral der Bewegung. Daher ist es nicht mehr nötig, die kanonischen Bewegungsgleichungen für dieses Paar zu lösen, die Ordnung des Problems verringert sich um 2.
Auch der Energiesatz (§12.3) läßt sich unter
diesem allgemeinen Fall subsummieren.
Die zyklische Variable ist die Zeit ![]() , der hiezu konjugierte Impuls
ist die negative Gesamtenergie
, der hiezu konjugierte Impuls
ist die negative Gesamtenergie ![]() .
.
Ein Integral der Bewegung ist im allgemeinen eine Funktion
![]() , die von der Zeit
, die von der Zeit ![]() unabhängig wird, wenn man für
unabhängig wird, wenn man für ![]() und
und ![]() die Lösungen der kanonischen Bewegungsgleichungen einsetzt. Diese Eigenschaft kann auch
ohne Kenntnis dieser Lösungen festgestellt werden. In die totale Zeitableitung des
Ausdruckes
die Lösungen der kanonischen Bewegungsgleichungen einsetzt. Diese Eigenschaft kann auch
ohne Kenntnis dieser Lösungen festgestellt werden. In die totale Zeitableitung des
Ausdruckes ![]() werden die kanonischen Bewegungsgleichungen eingesetzt:
werden die kanonischen Bewegungsgleichungen eingesetzt:
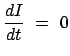 |
(1231) |
Bei der Lösung eines vorgegebenen mechanischen Problems wird man alle Integrale der Bewegung, die man kennt, heranziehen, um die Ordnung des Systems von Bewegungsgleichungen zu erniedrigen. Dazu muß man diese in die Bewegungsgleichungen einführen. Dies geschieht mittels der kanonischen Transformationen. Besonders erstrebenswert ist es, eine solche kanonische Transformation aufzufinden, daß in der neuen Hamiltonfunktion alle Variablen zyklisch sind. Dann gilt:
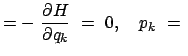 const. const. |
||
| (1232) | ||
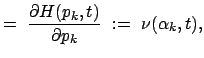 |
||
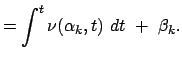 |
Damit ist das Problem vollständig gelöst. Ein Verfahren zum Auffinden solcher günstiger kanonischer Transformationen bietet die Hamilton-Jacobische Integrationstheorie.
Ein mechanisches System ist durch eine Hamiltonfunktion
![]() beschrieben, die Bewegung erfolgt gemäß den Hamiltonschen Bewegungsgleichungen.
Man geht zu
neuen kanonisch konjugierten Variablen
beschrieben, die Bewegung erfolgt gemäß den Hamiltonschen Bewegungsgleichungen.
Man geht zu
neuen kanonisch konjugierten Variablen ![]() über, für die man auch
eine neue Hamiltonfunktion
über, für die man auch
eine neue Hamiltonfunktion
![]() erhält. Es werden nur solche
Transformationen zugelassen, daß auch in den neuen Variablen die
Bewegungsgleichungen kanonische Form haben.
erhält. Es werden nur solche
Transformationen zugelassen, daß auch in den neuen Variablen die
Bewegungsgleichungen kanonische Form haben.
Die kanonischen Transformationen sind die nichtsingulären Transformationen
In den alten Variablen ![]() ,
, ![]() wird die Bewegung durch das
Hamiltonsche Prinzip, z.B.
in kanonischer Form (12.35), festgelegt:
wird die Bewegung durch das
Hamiltonsche Prinzip, z.B.
in kanonischer Form (12.35), festgelegt:
Wenn in den neuen Variablen ![]() das Hamiltonsche Prinzip die äquivalente
Form hat
das Hamiltonsche Prinzip die äquivalente
Form hat
Es ist nicht verlangt, daß die beiden Integrale in den Variationsprinzipien
(12.34) und (12.35) identisch werden, sondern nur, daß
sie gleichzeitig ihr Extremum annehmen: Wenn das Integral (12.34)
für die Funktion ![]() ,
, ![]() sein Extremum annimmt, so soll es das
Integral (12.35) für die Funktionen
sein Extremum annimmt, so soll es das
Integral (12.35) für die Funktionen ![]() ,
, ![]() tun,
die aus den
tun,
die aus den ![]() ,
, ![]() mittels der Transformationen(12.33)
hervorgehen. Dafür ist
notwendig und hinreichend, daß sich die beiden Integranden nur um die totale
Zeitableitung einer willkürlichen Funktion
mittels der Transformationen(12.33)
hervorgehen. Dafür ist
notwendig und hinreichend, daß sich die beiden Integranden nur um die totale
Zeitableitung einer willkürlichen Funktion ![]() unterscheiden
unterscheiden
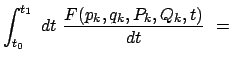 |
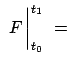 const. const. |
|
| (1238) | ||
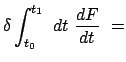 |
Gl. (12.37) und die Funktion ![]() sind äußerst wichtig für die
praktische Durchführung kanonischer Transformationen. F heißt die
erzeugende Funktion der kanonischen Transformation.
In Gl. (12.38) wurden alle
sind äußerst wichtig für die
praktische Durchführung kanonischer Transformationen. F heißt die
erzeugende Funktion der kanonischen Transformation.
In Gl. (12.38) wurden alle ![]() abhängigen Variablen
abhängigen Variablen ![]() ,
, ![]() ,
, ![]() ,
, ![]() als Argumente angegeben. Wegen der
Beziehungen (12.33) sind aber nur
als Argumente angegeben. Wegen der
Beziehungen (12.33) sind aber nur ![]() dieser Variablen
unabhängig; die übrigen
dieser Variablen
unabhängig; die übrigen ![]() Variablen können mittels
Gln. (12.33) durch die ersten
Variablen können mittels
Gln. (12.33) durch die ersten ![]() ausgedrückt werden. Es ist
für die weiteren Anwendungen notwendig, daß die erzeugende Funktion
ausgedrückt werden. Es ist
für die weiteren Anwendungen notwendig, daß die erzeugende Funktion ![]() bekannt ist und, daß sie von
bekannt ist und, daß sie von ![]() der alten und von
der alten und von ![]() der neuen
Variablen abhängt. Z.B. kann angenommen werden, daß
der neuen
Variablen abhängt. Z.B. kann angenommen werden, daß ![]() nur von den
nur von den ![]() und
und ![]() abhängt und dieses
abhängt und dieses ![]() wird in
Gl. (12.37) eingesetzt. Der resultierende Ausdruck wird
anschließend umgestellt.
wird in
Gl. (12.37) eingesetzt. Der resultierende Ausdruck wird
anschließend umgestellt.
Alle ![]() und
und ![]() sind voneinander unabhängig, ebenso deren Zeitableitungen.
Die obige Identität kann nur bestehen, indem die Koeffizienten aller
sind voneinander unabhängig, ebenso deren Zeitableitungen.
Die obige Identität kann nur bestehen, indem die Koeffizienten aller ![]() und
aller
und
aller ![]() , damit auch die rechte Seite Null sind. Dies führt zu folgender
Vorgangsweise:
, damit auch die rechte Seite Null sind. Dies führt zu folgender
Vorgangsweise:
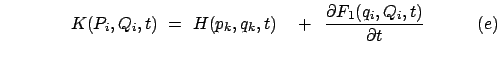
Als Beispiel wird am eindimensionalen harmonischen Oszillator die kanonische
Transformation durchgeführt, die von der folgenden Funktion ![]() erzeugt wird:
erzeugt wird:
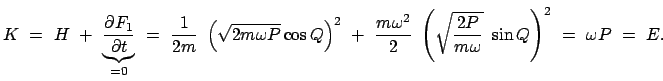 (e)
(e)
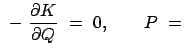 const. const. |
|||
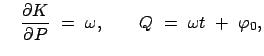 |
|||
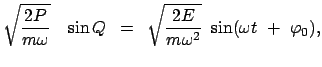 |
|||
Ein anderer Typ einer kanonischen Transformation ergibt sich, wenn man annimmt,
daß die erzeugende Funktion ![]() nur von den alten Koordinaten und den neuen
Impulsen abhängt. Es ist dann zweckmäßig, Gl. (12.37) durch Hinzufügen und
Abziehen der Summe
nur von den alten Koordinaten und den neuen
Impulsen abhängt. Es ist dann zweckmäßig, Gl. (12.37) durch Hinzufügen und
Abziehen der Summe
![]() umzuschreiben:
umzuschreiben:
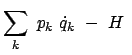 |
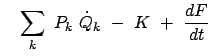 |
(1242) | |
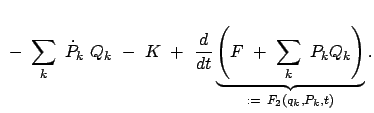 |
(1243) |
 |
(1246) | |
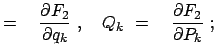 |
(1247) | |
| (1248) | ||
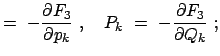 |
(1249) | |
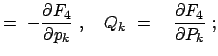 |
(1250) |
Der neue Ausdruck für die Hamiltonfunktion ist in allen Fällen der gleiche:
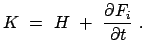
Hängt die kanonische Transformation nicht explizit von der Zeit ab (kanonische Transformation im engeren Sinn), dann gilt
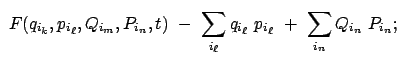 |
|||
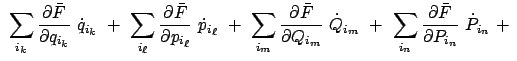 |
|||
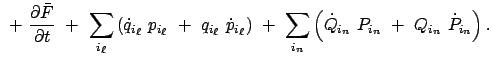 |
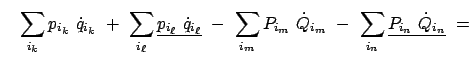 |
|||
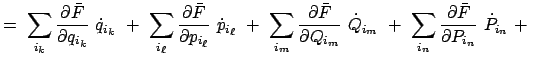 |
|||
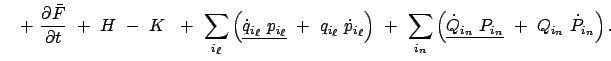 |
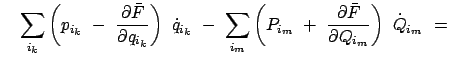 |
|||
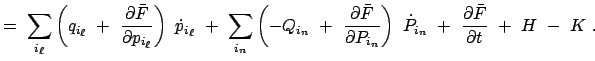 |
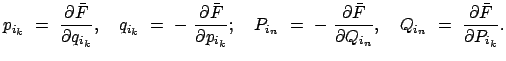
Es sind sehr viele verschiedenartige kanonische Transformationen möglich. Diese hängen nicht von der Hamiltonfunktion ab, sondern nur vom Freiheitsgrad. Eine gegebene kanonische Transformation kann auf alle Hamiltonfunktionen mit entsprechendem Freiheitsgrad angewendet werden. Da man aber mit einer kanonischen Transformation immer einen bestimmten Zweck verfolgt, nämlich die Reduktion der Ordnung des Systems von Bewegungsgleichungen durch Einführung der bekannten Integrale der Bewegung des Systems, muß man in jedem Fall die entsprechende kanonische Transformation zu eben diesem Zweck aufsuchen.
Vom mathematischen Standpunkt interessieren bei einer Transformation (hier bei einer kanonischen) immer die Größen, die bei diesen Transformationen unverändert, d.h. invariant, bleiben. Aus der Anwendung kommt andererseits der Wunsch, bei vorgegebenen Transformationen (12.33) feststellen zu können, ob diese kanonisch sind. Beide Probleme hängen zusammen und werden hier behandelt.
Wir beschränken uns bei den Untersuchungen dieses Paragraphen auf kanonische
Transformationen im engeren Sinn, in denen also die Zeit ![]() nicht explizit auftritt:
nicht explizit auftritt:
Wir nehmen nun an, daß die erzeugende Funktion in Gl. (12.37) so umgeformt worden
ist, daß sie nur von der neuen Variablen ![]() und
und ![]() abhängt. Die eben
erwähnte Gleichung nimmt dann folgende Gestalt an:121
abhängt. Die eben
erwähnte Gleichung nimmt dann folgende Gestalt an:121
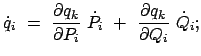 |
|||
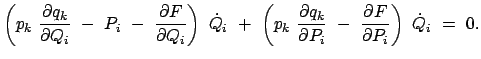 |
Das Kroneckersymbol folgt aus
![]() .
Die linke Seite jeder der obigen Gleichungen besteht aus 2f Termen, weil über den
Index k von 1 bis f zu summieren ist.
.
Die linke Seite jeder der obigen Gleichungen besteht aus 2f Termen, weil über den
Index k von 1 bis f zu summieren ist.
Die obigen Bedingungen, Gln. (12.57), sind notwendig und hinreichend für eine
kanonische Transformation. Aus der Existenz einer zweimal differenzierbaren erzeugenden
Funktion folgen diese Gleichungen. Umgekehrt, sind diese erfüllt, kann man den obigen Weg
rückwärts gehen und die Gln. (12.56) sind die Integrabilitätsbedingungen, die die
Existenz einer zu diesen Gleichungen gehörigen Funktion ![]() gewährleisten.
gewährleisten.
Die Ausdrücke in den Gln. (12.57) heißen Lagrange-Klammern und werden durch das folgende Symbol bezeichnet:
Zur Vereinfachung der weiteren Untersuchungen führen wir eine neue Schreibweise ein und fassen die kanonischen Variablen unter einem einheitlichen Symbol zusammen:
![$\displaystyle \left( \begin{array}{cc} \{ Q_i, Q_k \} & \{Q_i, P_k \} [2mm]
\{P_k, Q_i \} & \{P_k, P_i \} \end{array} \right) = G.
$](img3763.gif)
Ein weiterer Typ solcher Differentialausdrücke sind die Poisson-Klammern :
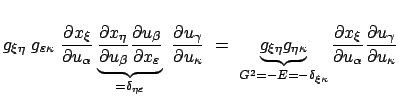 |
|||
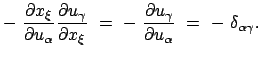 |
![$\displaystyle \underbrace{\{ Y_\alpha , Y_\beta \}_x}_{ = g_{ \alpha\beta}} [ Y_\beta , Y_\gamma]_x $](img3773.gif) |
|||
![$\displaystyle \underbrace{ - g_{\alpha \beta} g_{\alpha \sigma}}_{= \delta_{\beta \sigma}} \
[Y_\beta, Y_\gamma ]_x $](img3775.gif) |
(1271) |
Zum Beispiel ist die Transformation (vgl. (12.41))
![$\displaystyle P = \frac{1}{\omega} \left[ \frac{p^2}{2m} + \frac{m \o...
...2} q^2 \right] ,
\qquad
Q = \arctan \left( \frac{m \omega q}{p} \right)
$](img3777.gif)
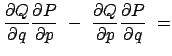 |
|||
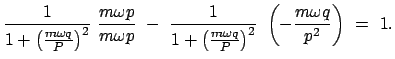 |
Auch die totale Zeitableitung einer beliebigen Größe
![]() läßt sich
durch Poissonklammern ausdrücken. Dabei wird zuerst die Kettenregel angewendet; danach
werden die kanonischen Bewegungsgleichungen eingesetzt.
läßt sich
durch Poissonklammern ausdrücken. Dabei wird zuerst die Kettenregel angewendet; danach
werden die kanonischen Bewegungsgleichungen eingesetzt.
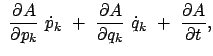 |
|||
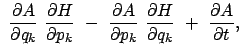 |
|||
![$\displaystyle [A, H] + \frac{\partial A}{\partial t} .$](img3785.gif) |
(1272) |
![$\displaystyle \frac{dA}{dt} = [A, H] + \frac{\partial A}{\partial t} = 0.
$](img3786.gif)
| (1273) |
Neben den Lagrange- und Poissonklammern, Gln. (12.58) und (12.67), die
Differentialinvarianten kanonischer Transformationen sind, gibt es auch
Integralinvarianten. Unter diesen betrachten wir nur eine, das
Volumen des Phasenraumes. Das Gebiet ![]() des Phasenraumes gehe
bei einer kanonischen Transformation in das Gebiet
des Phasenraumes gehe
bei einer kanonischen Transformation in das Gebiet ![]() über. Der
Satz von Liouville behauptet, daß die Volumina
über. Der
Satz von Liouville behauptet, daß die Volumina ![]() bzw
bzw
![]() dieser Gebiete gleich sind. Z.B stellt man sich vor, daß die
Phasenpunkte eines Systems von Teilchen ohne Wechselwirkung das Gebiet
dieser Gebiete gleich sind. Z.B stellt man sich vor, daß die
Phasenpunkte eines Systems von Teilchen ohne Wechselwirkung das Gebiet ![]() erfüllen.
Bei der zeitlichen Entwicklung sind diese in das Gebiet
erfüllen.
Bei der zeitlichen Entwicklung sind diese in das Gebiet ![]() gewandert (auch der
zeitliche Ablauf eines Systems kann durch eine kanonische Transformation
beschrieben werden):
gewandert (auch der
zeitliche Ablauf eines Systems kann durch eine kanonische Transformation
beschrieben werden):
| (1274) |
Die Inhalte der Gebiete G und G' sind:
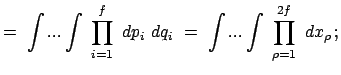 |
||
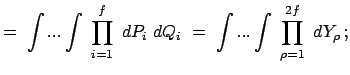 |
(1275) | |
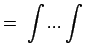 det det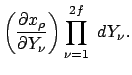 |
Der Satz von Liouville ist bewiesen, wenn gezeigt worden ist, daß die Jacobische Funktionaldeterminante:
Die oben benützten Relationen folgen aus (12.77):
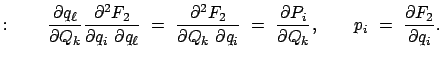
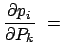 |
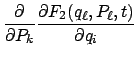 |
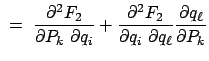 |
|
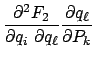 |
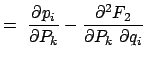 |
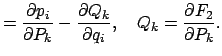 |
Wir suchen eine kanonische Transformation
Zum Beispiel für ein konservatives System mit Potential sind Hamiltonfunktion
und Hamilton-Jacobische Differentialgleichung
Die Hamilton-Jacobische Differentialgleichung ist eine partielle Differentialgleichung
für die ![]() Variablen
Variablen ![]() und
und ![]() . Die
. Die ![]() sind gemäß
Gl. (12.81) Konstante.
Die Differentialgleichung ist nicht linear und es ist daher aussichtslos, eine
allgemeine Lösung (die von willkürlichen Funktionen abhängt) aufsuchen zu
wollen. Doch wird eine solche gar nicht benötigt. Es genügt ein
vollständiges Integral, dies ist eine Funktion, die von allen
sind gemäß
Gl. (12.81) Konstante.
Die Differentialgleichung ist nicht linear und es ist daher aussichtslos, eine
allgemeine Lösung (die von willkürlichen Funktionen abhängt) aufsuchen zu
wollen. Doch wird eine solche gar nicht benötigt. Es genügt ein
vollständiges Integral, dies ist eine Funktion, die von allen ![]() ,
von
,
von ![]() und zusätzlich noch von f willkürlichen Integrationskonstanten
und zusätzlich noch von f willkürlichen Integrationskonstanten
![]() abhängt, die Differentialgleichung befriedigt und noch der
folgenden Bedingung genügt:
abhängt, die Differentialgleichung befriedigt und noch der
folgenden Bedingung genügt:
Außer den genannten Bedingungen ist das vollständige Integral beliebig. Nach
dem Satz von Jacobi erhält man damit die Lösung der ursprünglichen
Bewegungsgleichungen
Aus Gl. (12.89) berechnet man
![]() .
Diese in Gl. (12.88) eingesetzt, ergeben
.
Diese in Gl. (12.88) eingesetzt, ergeben
![]() .
Zum Beweis des Jacobischen
Satzes zeigen wir, daß diese Lösungen tatsächlich Gln. (12.86)
und (12.87) erfüllen.
Differenzieren wir Gl. (12.89) nach
.
Zum Beweis des Jacobischen
Satzes zeigen wir, daß diese Lösungen tatsächlich Gln. (12.86)
und (12.87) erfüllen.
Differenzieren wir Gl. (12.89) nach ![]() und Gl. (12.85)
nach den
und Gl. (12.85)
nach den ![]() .
.
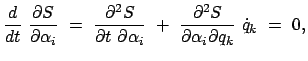 |
|||
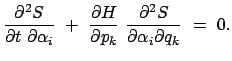 |
 |
|||
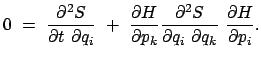 |
Die physikalische Deutung der Wirkungsfunktion findet man, indem man
Gl. (12.88) und (12.85) in die folgende Zeitableitung einsetzt:
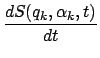 |
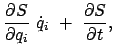 |
||
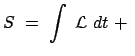 const. const. |
(1290) |
Indem man vom gegebenen Anfangspunkt
![]() zum gegebenen Endpunkt
zum gegebenen Endpunkt
![]() längs der eindeutig durch die beiden Punkte bestimmten Extremalen integriert,
so gilt für diese Wirkungsfunktion
längs der eindeutig durch die beiden Punkte bestimmten Extremalen integriert,
so gilt für diese Wirkungsfunktion ![]() auch Eikonal oder
geodätischer Abstand
der beiden Punkte genannt, die Differentialgleichung (12.84), wobei
auch Eikonal oder
geodätischer Abstand
der beiden Punkte genannt, die Differentialgleichung (12.84), wobei ![]() als Funktion
der Koordinaten des Endpunktes
als Funktion
der Koordinaten des Endpunktes ![]() aufgefasst wird. Daraus ergibt sich
auch, daß die Flächen
aufgefasst wird. Daraus ergibt sich
auch, daß die Flächen
![]() const.
const.![]() geodätisch äquidistant sind, d.h., daß,
wenn man das Integral
geodätisch äquidistant sind, d.h., daß,
wenn man das Integral
![]() längs einer zu den Flächen
längs einer zu den Flächen
![]() const.
const.![]() transversalen Extremale von
(12.91) integriert (es wird in dieser Theorie gezeigt, daß gerade
die Flächen
transversalen Extremale von
(12.91) integriert (es wird in dieser Theorie gezeigt, daß gerade
die Flächen
![]() const.
const.![]() Transversalflächen zu
einer Extremalenschar von (12.91) sind), erhält man für das zwischen zwei
Flächen erstreckte Integral unabhängig von der einzelnen Extremale denselben
Wert.
Transversalflächen zu
einer Extremalenschar von (12.91) sind), erhält man für das zwischen zwei
Flächen erstreckte Integral unabhängig von der einzelnen Extremale denselben
Wert.
![]() beschreibt eine den für die Bewegung in Frage kommenden Phasenraum
schlicht überdeckende Schar von Transversalflächen für die Extremalen von
(12.91), also für die möglichen Bahnkurven, vgl. Abbn. 12.7 und 12.8.
Allerdings werden durch eine einzige Flächenschar mit dem Parameter
beschreibt eine den für die Bewegung in Frage kommenden Phasenraum
schlicht überdeckende Schar von Transversalflächen für die Extremalen von
(12.91), also für die möglichen Bahnkurven, vgl. Abbn. 12.7 und 12.8.
Allerdings werden durch eine einzige Flächenschar mit dem Parameter ![]() nicht
alle möglichen Bahnkurven erfaßt, denn zu dem vollständigen Integral von (12.85)
gehört eine durch (12.89) implizit bestimmte 2
nicht
alle möglichen Bahnkurven erfaßt, denn zu dem vollständigen Integral von (12.85)
gehört eine durch (12.89) implizit bestimmte 2![]() -parametrige Schar von Bahnkurven.
Vor allem sieht man daraus auch sofort, daß die Funktion
-parametrige Schar von Bahnkurven.
Vor allem sieht man daraus auch sofort, daß die Funktion ![]() nicht eine bestimmte
Bewegung festlegen kann, denn diese wird durch die 2
nicht eine bestimmte
Bewegung festlegen kann, denn diese wird durch die 2![]() Parameter
Parameter
![]() bestimmt, während
bestimmt, während ![]() nur von
nur von ![]() Parametern
Parametern ![]() abhängt.
Es gehört also zu dem
vollständigen Integral noch eine f-fache Mannigfaltigkeit von Transversalflächen.
abhängt.
Es gehört also zu dem
vollständigen Integral noch eine f-fache Mannigfaltigkeit von Transversalflächen.
Leider gibt es kein allgemein verwendbares Verfahren zum Auffinden eines
vollständigen Integrals einer nichtlinearen partiellen Differentialgleichung;
man muß ein solches durch Probieren zu erraten suchen. Wenn die Lösung der
zugehörigen Newtonschen Bewegungsgleichung bekannt ist, gibt diese über
Gl. (12.88)
einen Hinweis über das Aussehen der Wirkungsfunktion ![]()
Als Beispiel zur Hamilton-Jacobischen Differentialgleichung wird zunächst der Harmonische Oszillator betrachtet:
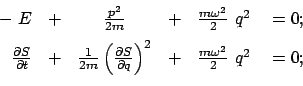 |
(1292) |
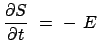 und
und| (1293) |
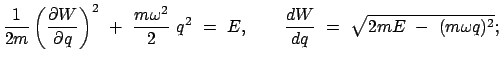 |
|||
![$\displaystyle W = \int \sqrt{()} dq = \frac{1}{2} \
\left[ q \sq...
...ga q)^2} + \frac{2E}{\omega} \arcsin\frac{m \omega q}{\sqrt{2mE}} \right] .$](img3868.gif) |
(1294) |
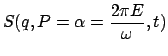 |
![$\displaystyle \frac{1}{2} \
\left[ q \sqrt{2mE - (m \omega q)^2} + \
\frac{2E}{\omega} \arcsin\frac{m \omega q}{\sqrt{2mE}} \right]$](img3871.gif) |
||
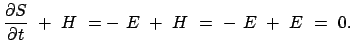 |
|||
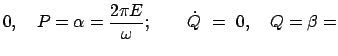 const. const. |
Als zweites Beispiel betrachten wir die Bewegung eines Teilchens in einem
räumlich homogenen, zeitlich linear anwachsenden Feld; die Newtonsche
Bewegungsgleichung und ihre Lösung sind
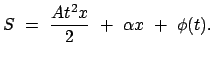 |
(1298) |
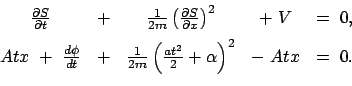
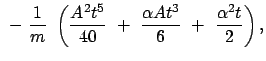 |
|||
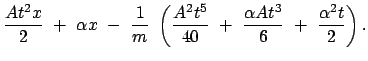 |
(1299) |
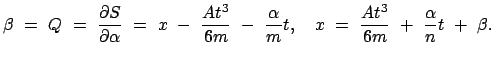
Bei einer gewöhnlichen Differentialgleichung 1. bzw. 2. Ordnung, z.B.
Als Beispiel einer partiellen Differentialgleichung wird zunächst die Wellengleichung betrachtet:
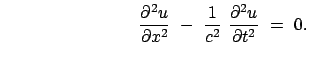 (a)
(a)| mit |
Beispiele solcher Funktionen sind in Abb. 12.6 dargestellt.
![\includegraphics[width=12.5cm]{K12Pulses}](img3907.gif)
|
Die Differentiagleichung (a) besagt nur, daß sich eine Störung mit der Geschwindigkeit ![]() längs der
längs der ![]() -Achse, (z.B. längs eines Drahtes oder einer Saite) ausbreitet. Die Gestalt
des Signals hängt von der Anregung am Anfang ab. Ein Puls mit unendlich steilen Flanken ist
zwar dort nicht differenzierbar, im übrigen ist er ein Lösung.
-Achse, (z.B. längs eines Drahtes oder einer Saite) ausbreitet. Die Gestalt
des Signals hängt von der Anregung am Anfang ab. Ein Puls mit unendlich steilen Flanken ist
zwar dort nicht differenzierbar, im übrigen ist er ein Lösung.
Die charakteristischen Lösungen (wie im Beispiel (c)) werden durch die charakteristischen Gleichungen der partiellen Differentialgleichung festgelegt; diese sind ein System von gewöhnlichen Differentialgeichungen. Bei der Hamilton-Jacobischen Differentialgleichung sind dies die Hamiltonschen Bewegungsgleichungen.
Bei einer nichtlinearen partiellen Differentialgleichung ist es sehr schwierig, oft sogar
unmöglich, die allgemeine Lösung anzugeben. Für die Anwendung in der Hamilton-Jacobischen
Integrationstheorie wird aber eine solche gar nicht benötigt. Sondern es genügt ein
vollständiges Integral. Ein solches ist eine gegebene Funktion der Variablen
![]() , die auch noch von
, die auch noch von ![]() Integrationkonstanten
Integrationkonstanten ![]() abhängt
abhängt
Meist wird zum Auffinden eines solchen vollständigen Integrals die Methode der Separation der Variablen (§12.8) herangezogen, wenn diese anwendbar ist.
Wenn die Lagrangefunktion, damit auch die Hamiltonfunktion, nicht explizit von der Zeit abhängen, ist die Hamiltonfunktion zeitlich konstant
| (12104) |
Die letzte Gleichung läßt sich auch in folgender Form schreiben:
| grad |
(12106) |
Der zeitunabhängige Anteil ![]() der Wirkungsfunktion
der Wirkungsfunktion ![]() kann auch als eine
selbständige Erzeugende einer kanonischen Transformation im engeren Sinn,
Gln. (12.52) und (12.53) betrachtet werden:
kann auch als eine
selbständige Erzeugende einer kanonischen Transformation im engeren Sinn,
Gln. (12.52) und (12.53) betrachtet werden:
Wird nun wieder die Gesamtenergie ![]() mit einer der willkürlichen
Integrationskonstanten, z.B. mit
mit einer der willkürlichen
Integrationskonstanten, z.B. mit
![]() identifiziert,
dann gilt (vgl. Gl. (12.105))
identifiziert,
dann gilt (vgl. Gl. (12.105))
Die physikalische Bedeutung der verkürzten Wirkungsfunktion ersieht man aus
der folgenden Zeitableitung (wobei Gl. (12.102) benützt wird):
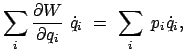 |
|||
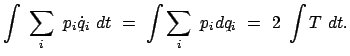 |
Um die Bedeutung von ![]() und
und ![]() deutlich zu machen, wird Gl. (12.102) noch genauer
untersucht. Die Flächen
deutlich zu machen, wird Gl. (12.102) noch genauer
untersucht. Die Flächen ![]() = const. bilden im
= const. bilden im
![]() der
der ![]() eine raumfeste
Flächenschar. Zur Zeit
eine raumfeste
Flächenschar. Zur Zeit ![]() = 0 fallen sie mit den Flächen
= 0 fallen sie mit den Flächen ![]() = const. zusammen;
im Laufe der Zeit wandern die Flächen
= const. zusammen;
im Laufe der Zeit wandern die Flächen ![]() = const. über die Flächen
= const. über die Flächen
![]() = const. hinweg. Wegen (12.88) bzw. (12.102) gilt, daß der Vektor
= const. hinweg. Wegen (12.88) bzw. (12.102) gilt, daß der Vektor
![]() senkrecht zu den Flächen
senkrecht zu den Flächen ![]() = const. steht, in diesem Falle also auch senkrecht
auf den Flächen
= const. steht, in diesem Falle also auch senkrecht
auf den Flächen ![]() = const. steht. Wenn man der Einfachheit halber die Bewegung
eines Teilchens in kartesischen Koordinaten betrachtet, so fällt der
kanonische Impuls mit dem gewöhnlichen zusammen und die Bahnkurven durchsetzen
die Flächen
= const. steht. Wenn man der Einfachheit halber die Bewegung
eines Teilchens in kartesischen Koordinaten betrachtet, so fällt der
kanonische Impuls mit dem gewöhnlichen zusammen und die Bahnkurven durchsetzen
die Flächen ![]() = const. senkrecht. Orthogonalität und Transversalität fallen
zusammen. Die Flächen konstanter Wirkung wandern durch den Raum; dies bedeutet
eine Ähnlichkeit mit der Optik, wo die Wellenflächen ebenfalls durch den Raum
wandern und die Lichtstrahlen orthogonale Trajektorien sind (s. Abbn.
12.7 und 12.8).
= const. senkrecht. Orthogonalität und Transversalität fallen
zusammen. Die Flächen konstanter Wirkung wandern durch den Raum; dies bedeutet
eine Ähnlichkeit mit der Optik, wo die Wellenflächen ebenfalls durch den Raum
wandern und die Lichtstrahlen orthogonale Trajektorien sind (s. Abbn.
12.7 und 12.8).
![\includegraphics[width=12.5cm]{K12WPlo1}](img3945.gif)
|
![\includegraphics[height=6.8cm]{K12WPlo2}](img3946.gif)
|
In §12.7 wurde ein vollständiges
Integral der Hamilton-Jacobischen
Differentialgleichung für gewisse eindimensionale Probleme durch Raten gefunden.
Diese Vorgangsweise wird umso schwieriger, je größer die Zahl der Variablen,
d.h. je größer der Freiheitsgrad ![]() ist. Ein in gewissen Fällen verwendbares
Verfahren zum Auffinden eines vollständigen Integrales der Hamilton-Jacobischen
Differentialgleichung (12.102
ist. Ein in gewissen Fällen verwendbares
Verfahren zum Auffinden eines vollständigen Integrales der Hamilton-Jacobischen
Differentialgleichung (12.102
![]() darf nur von der einzigen Variablen
darf nur von der einzigen Variablen ![]() abhängen. Wenn es gelingt, durch
einen derartigen Ansatz die partielle Differentialgleichung (12.112)
in f gewöhnliche Differentialgleichungen der Form
abhängen. Wenn es gelingt, durch
einen derartigen Ansatz die partielle Differentialgleichung (12.112)
in f gewöhnliche Differentialgleichungen der Form
Dann können die Gln. (12.114) nach der einzigen auftretenden Ableitung aufgelöst und integriert werden.
Der zu ![]() gehörige Anteil
gehörige Anteil ![]() genügt der Differentialgleichung
genügt der Differentialgleichung
Zuerst betrachten wir die Bewegung eines konservativen Systems mit einem
Freiheitsgrad, ![]() = 1. Der Zustand wird durch das Paar kanonisch konjugierter
Variablen
= 1. Der Zustand wird durch das Paar kanonisch konjugierter
Variablen ![]() und
und ![]() beschrieben. Ein System heißt periodisch, wenn es
nach einer endlichen Zeitdauer
beschrieben. Ein System heißt periodisch, wenn es
nach einer endlichen Zeitdauer ![]() wieder im gleichen Zustand ist.
wieder im gleichen Zustand ist.
Für ein konservatives System, das den Periodizitätsbedingungen (12.122) genügt,
wird nun ein vollständiges Integral der Hamilton-Jacobischen
Differentialgleichung (12.102) aufgesucht. Dies liefert die
erzeugende Funktion ![]() , Gl. (12.103), einer kanonischen
Transformation
, Gl. (12.103), einer kanonischen
Transformation
| (12123) | ||
| (12124) |
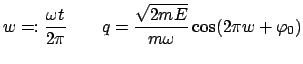 |
Beweis der Gl. (12.127): Die periodische Form ![]() aus
(12.125) läßt sich in eine Fourierreihe entwickeln:
aus
(12.125) läßt sich in eine Fourierreihe entwickeln:
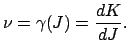 |
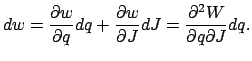 |
Da gemäß Gl. (12.126)
![]() const. ist, gilt für jede Phasenbahn
const. ist, gilt für jede Phasenbahn
![]() . Danach wird noch Gl. (12.131b) eingesetzt. Die totale
Änderung
. Danach wird noch Gl. (12.131b) eingesetzt. Die totale
Änderung ![]() von
von ![]() für den Umlauf des Systems um eine Periode ist
1, wenn für
für den Umlauf des Systems um eine Periode ist
1, wenn für ![]() das Phasenintegral (12.130) eingesetzt wird:
das Phasenintegral (12.130) eingesetzt wird:
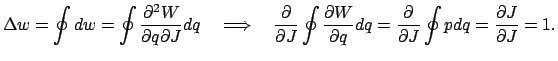 |
Zum Schluß das Ganze als einfaches Rezept zusammengefaßt:
Aus der Hamiltonfunktion berechnet man den Impuls als Funktion von ![]() und
und ![]() ;
damit das Phasenintegral als Funktion von
;
damit das Phasenintegral als Funktion von ![]() . Inversion gibt
. Inversion gibt ![]() als Funktion
von
als Funktion
von ![]() , damit die neue Hamiltonfunktion
, damit die neue Hamiltonfunktion ![]() . Die Grundfrequenz
. Die Grundfrequenz ![]() ist
die Ableitung von
ist
die Ableitung von ![]() nach
nach ![]() .
.
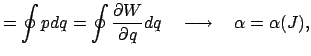 |
(12132) | |
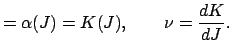 |
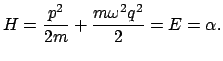 |
Ganz allgemein ist bei mehreren Freiheitsgraden eine Bewegung nur dann
periodisch, wenn die Perioden ![]() ,
, ![]() ,...,
,..., ![]() der einzelnen
Bewegungsrichtungen paarweise kommensurabel sind. Ist diese Bedingung nicht
erfüllt, dann kehrt das System nie zu irgendeinem in der Vergangenheit
angenommenen Zustand zurück, obwohl es in jedem Variablenpaar
der einzelnen
Bewegungsrichtungen paarweise kommensurabel sind. Ist diese Bedingung nicht
erfüllt, dann kehrt das System nie zu irgendeinem in der Vergangenheit
angenommenen Zustand zurück, obwohl es in jedem Variablenpaar ![]() ,
,![]() für sich periodisch ist. Ein solches System heißt mehrfach periodisch oder
fastperiodisch. Wieder können die Koordinaten in eine
für sich periodisch ist. Ein solches System heißt mehrfach periodisch oder
fastperiodisch. Wieder können die Koordinaten in eine ![]() -fache
Fourierreihe entwickelt werden (
-fache
Fourierreihe entwickelt werden (
![]() )
)
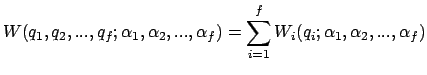 |
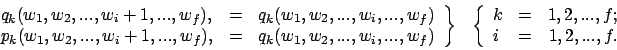 |
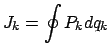 |
(12137) |
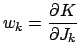
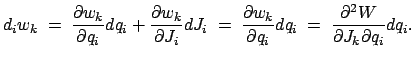 |
(12138) |
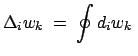 |
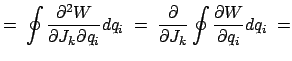 |
|
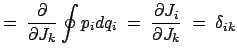 |
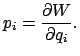
Als Anwendung der in §12.8 entwickelten Theorie wird die Lösung des Zentralkraft- und des Keplerproblems durch Separation der zugehörigen Hamilton-Jacobischen Differentialgleichung für die verkürzte Wirkungsfunktion vorgeführt. In Kugelkoordinaten lautet diese:
![$\displaystyle \left\{2m\left[V(r)-E\right] + \left(\frac{dW_1}{dr} \right)^2\ri...
...}{d\vartheta}\right)^2 + \frac{\alpha_{\varphi}^2}{\sin^2\vartheta}\right]\;=\;$](img4079.gif) const. const. |
(12143) |
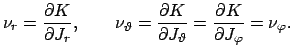
Die Gleichheit
![]() ergibt sich, weil der Integrand von (12.147c) nur
von der Summe
ergibt sich, weil der Integrand von (12.147c) nur
von der Summe
![]() abhängt. Das System hat daher
höchstens zwei verschiedene Eigenfrequenzen
abhängt. Das System hat daher
höchstens zwei verschiedene Eigenfrequenzen ![]() und
und
![]() , es ist entartet. Diese
Entartung hängt zusammen mit der Ebenheit der Bahn im Zentralfeld.
, es ist entartet. Diese
Entartung hängt zusammen mit der Ebenheit der Bahn im Zentralfeld.
Die Auswertung von (12.147c) für ein Coulombpotential ergibt:
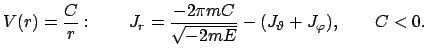 |
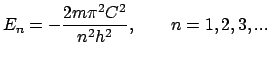
Wer nähere Details zur Berechnung der Phasenintegrale (12.147) erfahren möchte, kann sich direkt an den Vortragenden (B. S.) wenden.
Christian Sommer 2003-01-27