7.1 FUNCTION-Unterprogramme

7.1.1 Deklaration

Die Deklaration eines FUNCTION-Unterprogramms ist mit der Anweisung function auf folgende Arten möglich:

 function name
 function name(Eingangsparameter)
 function Ausgangsparameter = name
 function Ausgangsparameter = name(Eingangsparameter)

Gibt es mehrere Eingangsparameter sind diese durch Beistriche zu trennen. Gibt es mehrere Ausgangsparameter, ist die Liste der Parameter durch Beistriche zu trennen und mit eckigen Klammern zu umschließen.

 [aus_1, aus_2, ..., aus_n]

Ein Typ der Parameter muss, wie schon bei den Skripts, nicht explizit definiert werden, dieser ergibt sich durch die Zuweisungen innerhalb der Funktion.

Die Deklarationszeile sollte unmittelbar von einer oder von mehreren Kommentarzeilen gefolgt werden, die mit dem Prozentzeichen % beginnen. Diese werden beim Programmablauf ignoriert stehen aber als Hilfetext bei Aufruf von help name jederzeit zur Verfügung. Typischerweise sollen sie einem Benutzer mitteilen, was das jeweilige Programm macht.

Danach sollte eine Überprüfung der Eingabeparameter auf ihre Zulässigkeit bzw. auf ihre Anzahl erfolgen. Die Anzahl beim Aufruf muss nämlich nicht mit der Anzahl in der Deklaration übereinstimmen.

Danach folgen alle ausführbaren Anweisungen und die Zuweisung von Werten auf die Ausgangsparameter. Die Anzahl der Ausgangsparameter beim Aufruf muss ebenfalls nicht mit der Anzahl in der Deklaration übereinstimmen. Es muss aber sichergestellt werden, dass alle beim Aufruf geforderten Ausgangsparameter übergeben werden.

7.1.2 Resultat einer Funktion

Das Resultat einer Funktion ist - sofern es existiert - durch den Wert der Ausgangsparameter der Funktion gegeben. Diese können durch gewöhnliche Wertzuweisungen definiert werden; ihr Typ wird implizit über die Wertzuweisung bestimmt.

Normalerweise endet der Ablauf einer Funktion mit der Exekution der letzten Zeile. Es kann aber auch innerhalb der Funktion der Befehl return verwendet werden. Auch dies führt zu einer sofortigen Beendigung der Funktion. Dies kann z.B. bei Erfüllung einer Bedingung der Fall sein

 if Bedingung, return; end

Übergeben wird jener Wert der Ausgangsparameter, der zum Zeitpunkt der Beendigung gegeben ist. Werden die Eingangsparameter verändert, hat das keinen Einfluss auf den Wert dieser Variablen im rufenden Programm.

7.1.3 Aufruf einer Funktion

Der Aufruf einer Funktion erfolgt gleich wie der Aufruf eines MATLAB-Befehls:

 [aus_1, aus_2, ..., aus_n] = name(in_1, in_2, ..., in_m)

Viele der von MATLAB bereitgestellten Befehle liegen in Form von Funktionen vor. Sie können daher nicht nur exekutiert sondern auch im Editor angeschaut werden. Dies ist manchmal äußerst nützlich, da man dadurch herausfinden kann, wie MATLAB gewisse Probleme löst.

7.1.4 Überprüfung von Eingabeparametern

Für den Einsatz von Funktionen ist es sinnvoll, dass innerhalb von Funktionen die Gültigkeit der Eingabeparameter überprüft wird. Dies umfasst typischerweise die Überprüfung von

• der Dimension und Größe von Feldern,
• des Typs von Variablen, und
• des erlaubten Wertebereichs.

Damit soll ein Benutzer davor gewarnt werden, dass eine Funktion überhaupt nicht funktioniert oder für diese Parameter nur fehlerhaft rechnen kann. Dies sollte sinnvoll mit Fehlermitteilungen und Warnungen kombiniert werden, wie sie in 7.1.5 beschrieben werden.

In Ergänzung zu den bekannten logischen Abfragen, gibt es eine Reihe von MATLAB-Befehlen zur Überprüfung des Typs bzw. der Gleichheit oder des Inhalts. Sie geben für k=1, wenn die Bedingung erfüllt ist, bzw. k=0, wenn die Bedingung nicht erfüllt ist. Das Gleiche gilt für TF, außer dass hier ein logisches Feld zurückgegeben wird. Hier sind einige Beispiele angeführt. Eine gesamte Auflistung aller Befehle dieser Art findet man in der MATLAB-Hilfe für is.

k = ischar(S)	Zeichenkette
k = isempty(A)	Leeres Array
k = isequal(A,B,...)	Identische Größe und Inhalt
k = islogical(A)	Logischer Ausdruck
k = isnumeric(A)	Zahlenwert
k = isreal(A)	Reelle Werte
TF = isinf(A)	Unendlich
TF = isfinite(A)	Endliche Zahl
TF = isnan(A)	Not A Number
TF = isprime(A)	Primzahl

7.1.5 Fehler und Warnungen

Die MATLAB-Funktion error zeigt eine Nachricht im Kommandofenster an und übergibt die Kontrolle der interaktiven Umgebung. Damit kann man z.B. einen ungültigen Funktionsaufruf anzeigen.

 if Bedingung, error('Nachricht'); end

Analog dazu gibt es den Befehl warning. Dieser gibt ebenfalls die Meldung aus, unterbricht aber nicht den Programmablauf. Falls Warnungen nicht erwünscht bzw. doch wieder erwünscht sind, kann man mit warning off bzw. warning on aus- bzw. einschalten, ob man gewarnt werden will.

7.1.6 Optionale Parameter und Rückgabewerte

MATLAB unterstützt die Möglichkeit, Formalparameter eines Unterprogramms optional zu verwenden. Das heißt, die Anzahl der Aktualparameter kann kleiner sein, als die Anzahl der Formalparameter.

Formalparameter

sind jene Parameter, die in der Deklaration der Funktion spezifiziert werden.

Aktualparameter

sind jene Parameter, die beim Aufruf der Funktion spezifiziert werden.

Bei einem Aufruf eines FUNCTION-Unterprogramms werden die Aktualparameter von links nach rechts mit Formalparametern assoziiert. Werden beim Aufruf einer Funktion weniger Aktualparameter angegeben, so bleiben alle weiteren Formalparameter ohne Wert, sie sind also undefiniert.

Werden solche undefinierten Variablen verwendet, beendet MATLAB die Abarbeitung des Programms mit einer Fehlermeldung. Der Programmierer hat zwei Möglichkeiten mit dieser Situation umzugehen:

• Sicherstellen, dass nicht übergebene Parameter nicht verwendet werden.
• Vergabe von Defaultwerten für nicht übergebene Parameter am Anfang des Programms.

Zu diesem Zweck hat MATLAB die beiden Variablen nargin und nargout, die nach dem Aufruf einer Funktion die Anzahl der aktuellen Eingabe-, bzw. Ausgabeparameter angeben. Mit Hilfe von nargin kann ganz leicht die Vergabe von Defaultwerten geregelt werden.

Ist die Anzahl der aktuellen Ausgabeparameter kleiner als die der Formalparameter, kann man sich das Berechnen der nicht gewünschten Ergebnisse sparen. Dies macht vor allem bei umfangreichen Rechnungen mit großem Zeitaufwand Sinn und kann helfen sehr viel Rechenzeit einzusparen.

Eine mögliche Realisierung einer solchen Überprüfung kann folgendermaßen aussehen:

 function [o1,o2]=name(a,b,c,d)
 % Hilfetext
 if nargin<1, a=1; end
 if nargin<2, b=2; end
 if nargin<3, c=3; end
 if nargin<4, d=4; end

 if nargout>0, o1 = a+b; end
 if nargout>1, o2 = c+d; end

Eine zusätzlich Möglichkeit bietet auch die Verwendung der Funktion isempty. Damit kann überprüft werden, ob ein Übergabeparameter als leeres Feld [] übergeben wird. Damit könnte obiges Beispiel so aussehen:

 function [o1,o2]=name(a,b,c,d)
 % Hilfetext
 if nargin<1, a=1; end, if isempty(a), a=1; end
 if nargin<2, b=2; end, if isempty(b), b=2; end
 ...

Nun würde auch ein Aufruf [x,y]=name([],4,5,6) den Defaultwert für a setzen.

7.1.7 Inline-Funktionen

Einfache Funktionen, die in einer Befehlszeile Platz finden, können auch mit Hilfe der Funktion inline definiert werden.

 f1 = inline('x.^n .* exp(-x.^2)', 'x', 'n');
 f2 = inline('m*exp(-n*(x.^2 + y.^2))', 'x', 'y', 'm', 'n');

Dabei muss als erster String die Funktion angegeben, der dann von Strings für die Inputparameter gefolgt wird. Die Reihenfolge der Strings für die Inputparameter entscheidet über die Reihenfolge beim Aufruf. Es ist in manchen Fällen auch möglich, keine Inputparameter zu übergeben. Von einer Verwendung dieser Eigenschaft wird jedoch abgeraten.

Wichtig ist auch hier, dass die Funktionen mit den richtigen Operatoren geschrieben werden, sodass eine Verwendung auch für Vektoren und Arrays möglich ist.

Bei der Definition der inline-Funktion wird keine Überprüfung der Syntax der Funktion und auch keine Überprüfung der Übergabeparameter durchgeführt. Daher werden in dieser Phase keine Fehler erkannt, die dann erst bei der Verwendung auftreten. Typische Fehlermitteilungen sind dann

 Error using ==> inlineeval
 Error in inline expression ==> ....

7.1.8 Unterprogramme als Parameter

Bisher wurden Datenobjekte als Parameter eines Unterprogramms betrachtet. Man kann jedoch auch Unterprogramme als Parameter an weitere Unterprogramme übergeben. In diesem Fall wird dem aufgerufenen Unterprogramm der Name des Unterprogramms als String oder als Funktionenhandle übergeben. Dies funktioniert natürlich auch mit inline-Funktionen, in diesem Fall muss diese Funktion direkt übergeben werden.

Als Beispiel sollen hier die Funktionen quad, quadl und dblquad verwendet werden, wobei zuerst die inline-Funktionen aus 7.1.7 Verwendung finden.

Die beiden Unterprogramme quad und quadl unterscheiden sich durch die verwendete numerische Methode, quad verwendet eine adaptive Simpson Methode und quadl verwendet eine adaptive Lobatto Methode.

Berechnet sollen z.B. folgende Integrale werden.

$$A_{1} = \int_{a}^{b} dx \; x^{n}\exp(-x^{2})$$ (7.1)

$$A_{2} = \int_{a}^{b}\int_{c}^{d} dxdy \; m \exp \left( -n(x^{2} + y^{2}) \right) \;$$ (7.2)

 A1 = quadl(f1, a, b, TOL, ANZEIGE, n)
 A1 = quadl(f1, a, b, [],  [],      n)

 A2 = dblquad(f2, a, b, c, d, TOL, METHODE, m, n)
 A2 = dblquad(f2, a, b, c, d, [],  [],      m, n)

Die Reihenfolge der Inputparameter für f1 bzw. f2 ist ganz wichtig, es müssen immer jene Variablen vorne stehen über die integriert wird. Erst danach kann einen beliebige Anzahl von anderen Größen folgen, die durch die Integrationsroutine nur durchgeschleust werden, d.h. diese zusätzlichen Größen haben mit der Integrationsroutine nichts zu tun, werden aber für die Auswertung des Integranden benötigt.

Die optionalen Werte für TOL, ANZEIGE und METHODE müssen nicht übergeben werden. Falls man, wie in unseren Beispielen, weitere Parameter für die zu integrierende Funktion braucht, müssen für TOL, ANZEIGE und METHODE entweder Werte oder leere Arrays [] übergeben werden. Die Defaultwerte sind

 TOL = 1.e-6, ANZEIGE = 0, METHODE='quad'

Größere Werte für TOL resultieren in einer geringeren Anzahl von Funktionsaufrufen und daher einer kürzeren Rechenzeit, verschlechtern aber natürlich die Genaugkeit des Ergebnisses.

Setzt man ANZEIGE = 1, bekommt man eine Statistik der Auswertung am Schirm ausgegeben. Bei der METHODE hat man die Wahl zwischen 'quad' und 'quadl', wobei dies den MATLAB-Funktionen quad und quadl entspricht. In Prinzip könnte man auch eine eigene Integrationsroutine zur Verfügung stellen, die den gleichen Konventionen wie quad folgen muss.

Liegen die Funktionen nicht als inline-Funktionen sondern als Funktionen in den Files ff1.m bzw. ff2.m vor, so hat man zwei Möglichkeiten, (i) Angabe des Namens als String 'ff1' oder als Funktionshandle @ff1. Damit kann man obige Befehle z.B. als

 A1 = quadl('ff1', a, b, TOL, ANZEIGE, n)
 A1 = quadl(@ff1,  a, b, TOL, ANZEIGE, n)

 A2 = dblquad('ff2', a, b, c, d, TOL, 'quadl', m, n)
 A2 = dblquad(@ff2,  a, b, c, d, TOL, @quadl,  m, n)

schreiben. Die Funktionen müssen der Konvention für die Erstellung von Unterprogrammen folgen und müssen mit dem Befehl feval auswertbar sein.

 feval('ff1', x, n)        feval(@ff1, x, n) 
 feval('ff2', x, y, m, n)  feval(@ff2, x, y, m, n)

Wichtig ist vor allem auch, dass sie für beliebige Vektoren x und y auszuwerten sind.

7.1.9 Globale Variablen

In MATLAB ist es möglich, ein Set von Variablen für eine Reihe von Funktionen global zugänglich zu machen, ohne diese Variablen durch die Inputliste zu übergeben. Dafür steht der Befehl global var1 var2 zur Verfügung. Er muss in jeder Programmeinheit ausgeführt werden, wo diese Variablen zur Verfügung stehen sollen, d.h. die Variablen sind nicht automatisch überall verfügbar.

Das global-Statement soll vor allen ausführbaren Anweisungen in einem Skript oder einem function-Unterprogramm angeführt werden. Da diese Variablennamen in weiten Bereichen ihre Gültigkeit haben können, empfiehlt es sich längere und unverwechselbare Namen zu verwenden, damit sie sich nicht mit lokalen Variablennamen decken.

Mit dem Befehl global gibt es also neben den Input- und Outputlisten eine weitere Möglichkeit Informationen zwischen Skripts und Funktionen, bzw. zwischen Funktionen untereinander auszutauschen. Dies ist vor allem dann interessant, wenn Funktionen als Parameter übergeben werden und man sich beim Aufruf der ``Zwischenfunktion'' (z.B. quadl) keine Gedanken über die weiteren Parameter, die eventuell im Unterprogramm noch gebraucht werden, machen will.

Das Skript

  global flag
  k = 3;
  flag = 'a';
  A_a  = quadl(ifunc,0,1,[],[],k);
  flag = 'b';
  A_b  = quadl(ifunc,0,1,[],[],k);
  clear global flag

berechnet mit der Funktion ifunc

  function [y] = ifunc(x,k)
  global flag
  switch flag
  case 'a', y = sin(k*x);
  case 'b', y = cos(k*x);
  otherwise, error('flag existiert nicht');
  end

die Integrale über zwei verschiedene mathematische Funktionen.

Am Ende solcher Berechnungen sollte man in der übergeordneten Einheit diese Variablen wieder löschen. Das geschieht mit clear global var1 var2, damit verschwinden die Variablen aus allen lokalen Speicherbereichen und sind nirgendwo mehr zugänglich.

7.1.10 Beispiele

Einfaches Beispiel (tfunc1.m):

function f = tfunc1(x)
% Einfachste Funktion mit einer Input-Variablen und einer
% Output-Variablen.
% 
% Berechnet die Funktion f(x) = x^2 * sin(x)
%  
% Aufruf: f = tfunc1(x)
% Input:  x   double array x
% Output: f   double array x.^2 .* sin(x)
  
% Der erste Kommentarblock wird bei Aufruf des Befehls 
%            help tfunc1 
% angezeigt
  
% Hier beginnt nun die Berechnung 
  f = x.^2 .* sin(x);

Beispiel mit mehreren Input- und Outputvariablen (tfunc2.m):

function [f1,f2] = tfunc2(x,a,b) 
% Funktion mit drei Input-Variablen und zwei Output-Variablen.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * sin(x)
%                          f2(x) = a * x^2 * sin(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc2(x,a,b)
% Input:  x   double array 
%         a   double scalar
%         b   double scalar
% Output: f1  double array   f1 = a * x.^2 .* sin(x)
%         f2  double array   f2 = a * x.^2 .* sin(x) + b * x
  
  f1 = a * x.^2 .* sin(x);
  f2 = f1 + b * x; % f1 verwendet um Rechenzeit zu sparen

Beispiel mit mehreren Input- und Outputvariablen, wobei Defaultwerte für einige Inputvariablen gesetzt werden. (tfunc2a.m):

function [f1,f2] = tfunc2a(x,a,b) 
% Funktion mit drei Input-Variablen und zwei Output-Variablen.
% Setzen von Default-Werten.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * sin(x)
%                          f2(x) = a * x^2 * sin(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc2a(x,a,b) 
% Input:  x   double array 
%         a   double scalar, optional, default a=1
%         b   double scalar, optional, default b=2
% Output: f1  double array   f1 = a * x.^2 .* sin(x)
%         f2  double array   f2 = a * x.^2 .* sin(x) + b * x

% Die Variable nargin enthaelt nach dem Aufruf der Funktion tfunc2a
% die Anzahl der übergebenen Input-Variablen. Die Variable nargout 
% enthält die Anzahl der Output-Variablen.
% 
% z.B.:  [r1,r2] = tfunc2a([1:10],3,4) => nargin=3, nargout=2
%         r1     = tfunc2a([1:10],3)   => nargin=2, nargout=1
%                  tfunc2a             => nargin=0, nargout=0
%
% Diese Variablen kann man nun zum Steuern der Verhaltens der Funktion,
% zum Setzen von Defaultwerten und zur Entscheidung, welche
% Output-Variablen berechnet werden sollen, verwenden.
  
% Der Befehl isempty(a) überprüft ob die Variable a eine leeres Array []
% ist. Damit kann man auch den Defaultwert von a verwenden, obwohl man b
% eingibt: 
% z.B.:  [r1,r2] = tfunc2a([1:10],[],4)
  if nargin<1, error('Aufruf mit [f1,f2] = tfunc2a(x,a,b)'); end
  if nargin<2,   a = 1; end, if isempty(a), a = 1; end
  if nargin<3,   b = 2; end, if isempty(b), b = 2; end
  f1 = a * x.^2 .* sin(x);
  if nargout>1, f2 = f1 + b * x; end

Beispiel mit mehreren Input- und Outputvariablen, wobei auch globale Variable verwendet werden. (tfunc2b.m):

function [f1,f2] = tfunc2b(x) 
% Funktion mit drei Input-Variablen und zwei Output-Variablen. Verwendung
% von globalen Variablen für die Variablen a und b.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * sin(x)
%                          f2(x) = a * x^2 * sin(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc2b(x)
% Global: a   double scalar, optional, default a=1
%         b   double scalar, optional, default b=2  
% Input:  x   double array 
% Output: f1  double array   f1 = a * x.^2 .* sin(x)
%         f2  double array   f2 = a * x.^2 .* sin(x) + b * x

% Definition von globalen Variablen. Wurden diese vorher noch nicht
% definiert, existieren sie nach der Anweisung global als leere Arrays. 
  global a b
  if nargin<1, error('Aufruf mit [f1,f2] = tfunc2a(x,a,b)'); end
  if isempty(a), a = 1; end
  if isempty(b), b = 2; end
  f1 = a * x.^2 .* sin(x);
  if nargout>1, f2 = f1 + b * x; end

Beispiel mit mehreren Input- und Outputvariablen mit Summation zur Berechnung von:

$$f_1(x) = \sum_{k=1}^{n} a_k x^2 \sin(a(k) x), \qquad f_2(x) = \sum_{k=1}^{n} a_k x^2 \sin(a(k) x) + b_k x$$

(tfunc2c.m):

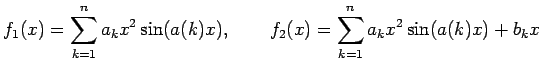
function [f1,f2] = tfunc2c(x,a,b) 
% Funktion mit drei Input-Variablen und zwei Output-Variablen.
% Setzen von Default-Werten.
%
% Bei diesem Beispiel können die Variablen a und b Vektoren sein. 
% 
% Berechnet die Funktionen f1(x) = a(1) * x^2 * sin(x)
%                                + a(2) * x^2 * sin(x)
%                                + ...
%                          f2(x) = a(1) * x^2 * sin(x) + b(1) * x
%                                + a(2) * x^2 * sin(x) + b(2) * x
%                                + ...
%  
% Aufruf: [f1,f2] = tfunc2c(x,a,b) 
% Input:  x   double array 
%         a   double array, optional, default a=[1,2]
%         b   double array, optional, default b=[2,4]
% Output:                    Summation ueber alle k
%         f1  double array   f1 = a(k) * x.^2 .* sin(a(k)*x)
%         f2  double array   f2 = a(k) * x.^2 .* sin(a(k)*x) + b(k) * x

  if nargin<1, error('Aufruf mit [f1,f2] = tfunc2c(x,a,b)'); end
  if nargin<2,   a = [1,2]; end, if isempty(a), a = [1,2]; end
  if nargin<3,   b = [2,4]; end, if isempty(b), b = [2,4]; end
  % Output-Groessen werden mit 0 initialisiert
  f1 = zeros(size(x)); f2 = f1;
  % Summation über alle f1(k) und f2(k)
  for k = 1:length(a)
    h1 = a(k) * x.^2 .* sin(a(k)*x);
    h2 = h1 + b(k) * x;
    f1 = f1 + h1;
    f2 = f2 + h2;
  end

Beispiel mit Fallunterscheidung (tfunc3.m):

function [f1,f2] = tfunc3(f,x,a,b) 
% Funktion mit vier Input-Variablen und zwei Output-Variablen.
% Die Variable f dient dabei zur Fallunterscheidung.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * f(x)
%                          f2(x) = a * x^2 * f(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc3(f,x,a,b)
% Input:  f   char   array,  {'sin', 'cos', 'tan', 'cot'}, default 'sin'
%         x   double array 
%         a   double scalar, optional, default a=1
%         b   double scalar, optional, default b=2
% Output: f1  double array   f1 = a * x.^2 .* f(x)
%         f2  double array   f2 = a * x.^2 .* f(x) + b * x

  if nargin<2, error('Aufruf mit [f1,f2] = tfunc3(f,x,a,b)'); end
  if isempty(f), f = 'sin'; end;
  if nargin<3, a = 1; end; if isempty(a), a = 1; end;
  if nargin<4, b = 2; end; if isempty(b), b = 2; end;
  
  % Die Fallunterscheidung wird mit einer switch-case-Konstruktion
  % durchgeführt, wobei die die String-Variable f als Schalter dient.
  switch f
   case 'sin'
    f1 = a * x.^2 .* sin(x);
   case 'cos'
    f1 = a * x.^2 .* cos(x);
   case 'tan'
    f1 = a * x.^2 .* tan(x);
   case 'cot'
    f1 = a * x.^2 .* cot(x);
   otherwise
    error(['Fall ',f,' existiert nicht!']);
  end
  if nargout>1, f2 = f1 + b * x; end

Beispiel mit Fallunterscheidung und automatischer Konstruktion von Funktionsaufrufen (tfunc3a.m):

function [f1,f2] = tfunc3a(f,x,a,b) 
% Funktion mit vier Input-Variablen und zwei Output-Variablen.
% Die Variable f dient dabei zur Fallunterscheidung.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * f(x)
%                          f2(x) = a * x^2 * f(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc3a(f,x,a,b)
% Input:  f   char   array,  {'sin', 'cos', 'tan', 'cot'}, default 'sin'
%         x   double array 
%         a   double scalar, optional, default a=1
%         b   double scalar, optional, default b=2
% Output: f1  double array   f1 = a * x.^2 .* f(x)
%         f2  double array   f2 = a * x.^2 .* f(x) + b * x

  if nargin<2, error('Aufruf mit [f1,f2] = tfunc3a(f,x,a,b)'); end
  if isempty(f), f = 'sin'; end;
  if nargin<3, a = 1; end; if isempty(a), a = 1; end;
  if nargin<4, b = 2; end; if isempty(b), b = 2; end;
  
  % Die String-Variable f wird nun einerseits als Schalter, aber auch zur
  % Konstruktion der Funktion verwendet.
  switch f
   case {'sin', 'cos', 'tan', 'cot'}
    % Zusammensetzen einer Zeichenkette [s1,s2,s3]
    e_string = ['a * x.^2 .* ',f,'(x)'];
    disp(['Berechnung mit: ',e_string]);
    % Mit eval kann man den Inhalt einer Zeichenkette als Kommando
    % ausführen. 
    % z.B.: f = eval('3*x+2'); equivalent mit f = 3*x+2;
    f1 = eval(e_string);
   otherwise
    error(['Fall ',f,' nicht erlaubt!']);
  end
  if nargout>1, f2 = f1 + b * x; end

Beispiel mit Fallunterscheidung, automatischer Konstruktion von Funktionsaufrufen und rekursivem Aufruf. (tfunc3b.m):

function [f1,f2] = tfunc3b(varargin) 
% Funktion mit vier Input-Variablen und zwei Output-Variablen.
% Die Variable varargin ist eine Zelle, die alle übergebenen
% Input-Variablen enthält.
% 
% Berechnet die Funktionen f1(x) = a * x^2 * f(x)
%                          f2(x) = a * x^2 * f(x) + b * x
%  
% Aufruf: [f1,f2] = tfunc3b(f,x,a,b)
% Input:  f   char   array,  {'sin', 'cos', 'tan', 'cot'}, default 'sin'
%         x   double array 
%         a   double scalar, optional, default a=1
%         b   double scalar, optional, default b=2
% Output: f1  double array   f1 = a * x.^2 .* f(x)
%         f2  double array   f2 = a * x.^2 .* f(x) + b * x

  if nargin<1, error('Aufruf mit [f1,f2] = tfunc3b(f,x,a,b)'); end
  if ~ischar(varargin{1}) % Erstes Element der Zelle kein String
    [f1,f2] = tfunc3b('sin',varargin{:}); % Rekursiver Aufruf von tfunc3b
    % Übergabe von 'sin' und aller Parameter vom ersten Aufruf.	
    return % Beendet ersten Aufruf der Funktion
  end
  
  f = varargin{1}; % Erster Übergabeparameter
  if nargin<2, 
    error('Aufruf mit [f1,f2] = tfunc3b(f,x,a,b)');
  else
    x = varargin{2}; % Zweiter Übergabeparameter
  end
  
  if nargin<3, a = 1; else, a = varargin{3}; end
  if isempty(a), a = 1; end
  if nargin<4, b = 2; else, b = varargin{4}; end
  if isempty(b), b = 2; end
    
  % Die String-Variable f wird nun einerseits als Schalter, aber auch zur
  % Konstruktion der Funktion verwendet.
  switch f
   case {'sin', 'cos', 'tan', 'cot'}
    % Zusammensetzen einer Zeichenkette [s1,s2,s3]
    e_string = ['a * x.^2 .* ',f,'(x)'];
    disp(['Berechnung mit: ',e_string]);
    % Mit eval kann man den Inhalt einer Zeichenkette als Kommando
    % ausführen. 
    % z.B.: f = eval('3*x+2'); equivalent mit f = 3*x+2;
    f1 = eval(e_string);
   otherwise
    error(['Fall ',f,' nicht erlaubt!']);
  end
  if nargout>1, f2 = f1 + b * x; end