8.2 Nullstellen und charakteristische Polynome
se:polynome_nullstellen
Die Nullstellen eines Polynoms können mit dem Befehl
r=roots(p)
gefunden werden. Umgekehrt erzeugt der Befehl
p=poly(r)
das Polynom p, wenn r ein Vektor von
Nullstellen ist. Für Vektoren sind roots
und poly
inverse
Funktionen bis auf Skalierungsfaktoren, Reihenfolge der Nullstellen und
Rundungsfehler.
Der Aufruf von c=poly(A), wobei 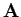 eine
eine 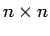 Matrix
sein muss, liefert das charakteristische Polynom
Matrix
sein muss, liefert das charakteristische Polynom 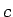 der Matrix
der Matrix 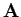 . Das
charakteristische Polynom ergibt sich aus folgender Determinante
. Das
charakteristische Polynom ergibt sich aus folgender Determinante
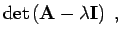 |
(8.5) |
wobei 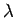 die Eigenwerte der Matrix
die Eigenwerte der Matrix 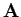 , bzw. die Nullstellen des
charakteristischen Polynoms
, bzw. die Nullstellen des
charakteristischen Polynoms 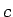 sind.
sind.
Dies soll am Beispiel von
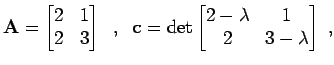 |
(8.6) |
demonstriert werden, wobei sich hier als Lösung
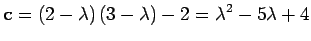 |
(8.7) |
ergibt. Die Darstellung in MATLAB ergibt c=[1,-5,4] und die
Nullstellen des charakteristischen Polynoms liegen bei
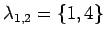 .
.
Das Pascal'sche Dreieck
kann auch in Form der Pascal'schen Matrix, hier für 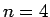 mit z.B. dem
MATLAB-Befehl P=pascal(4)
mit z.B. dem
MATLAB-Befehl P=pascal(4)
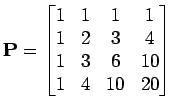 |
(8.9) |
dargestellt werden. Das charakteristische Polynom kann nun mit dem Befehl
p=poly(P)
erzeugt werden und ergibt [1,-29,72,-29,1],
was folgendem Polynom entspricht
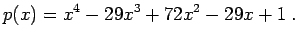 |
(8.10) |
Pascal'sche Matrizen haben die kuriose Eigenschaft, dass der Vektor der
Koeffizienten des charakteristischen Poylnoms ``palindromic'' ist, d.h. er
ergibt das Selbe von vorne und von hinten gelesen.
Evaluiert man das charakteristische Polynom nun im Sinne der
Matrixmultiplikation, so erhält man mit R=polyvalm(p,P)
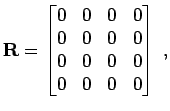 |
(8.11) |
d.h. die Nullmatrix. Dies ist eine Folge des Cayley-Hamilton Theorems, dass
besagt das eine Matrix ihre eigene charakteristische Gleichung erfüllt.
Winfried Kernbichler
2005-04-26
![]() eine
eine ![]() Matrix
sein muss, liefert das charakteristische Polynom
Matrix
sein muss, liefert das charakteristische Polynom ![]() der Matrix
der Matrix ![]() . Das
charakteristische Polynom ergibt sich aus folgender Determinante
. Das
charakteristische Polynom ergibt sich aus folgender Determinante