Next: 10.2 Interpolation Up: 10. Anwendungen Previous: 10. Anwendungen Contents
Kurvenanpassung, oder auch Fitten genannt, ist eine Technik mit der man
versucht, eine gegebene mathematische Modellfunktion bestmöglich an
Datenpunkte anzupassen. Der einfachste Fall ist wohl die Bestimmung einer
Ausgleichsgeraden, wo die Koeffizienten ![]() und
und ![]() des Polynoms ersten
Grades
des Polynoms ersten
Grades
![]() so bestimmt werden, dass die Summe der
Abstandsquadrate von den Datenpunkten den kleinstmöglichen Wert annimmt.
so bestimmt werden, dass die Summe der
Abstandsquadrate von den Datenpunkten den kleinstmöglichen Wert annimmt.
Diese Minimierung der Summe der Abstandsquadrate bezeichnet man als ''Least
Squares''-Verfahren. Bei Vorliegen von ![]() Datenpunkten
Datenpunkten
![]() und
unter der Annahme, dass die Modellfunktion mit
und
unter der Annahme, dass die Modellfunktion mit ![]() bezeichnet wird, kann
die Summe der Abstandsquadrate geschrieben werden als
bezeichnet wird, kann
die Summe der Abstandsquadrate geschrieben werden als
Im Wesentlichen sind zwei unterschiedliche Klassen von Modellfunktionen zu
unterscheiden, solche die lineare Funktionen der Parameter ![]() sind und
solche die nichtlineare Funktionen der Parameter
sind und
solche die nichtlineare Funktionen der Parameter ![]() sind. Lineare
Funktionen sind Polynome bzw. Funktionen, die man im weitesten Sinne als
verallgemeinerte Polynome bezeichnen könnte
sind. Lineare
Funktionen sind Polynome bzw. Funktionen, die man im weitesten Sinne als
verallgemeinerte Polynome bezeichnen könnte
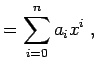 |
(10.2) | |
| (10.3) | ||
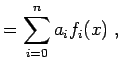 |
(10.4) | |
| (10.5) |
| (10.6) | ||||
| (10.7) |
| (10.8) | ||
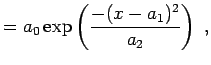 |
(10.9) | |
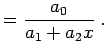 |
(10.10) |
Ein wichtiger Schritt bei der Kurvenanpassung ist die Auswahl der Modellfunktion. Wann immer es möglich ist, lässt man sich von einem zugrunde liegenden physikalischen Modell bei der Auswahl leiten:
Ist die Wahl auf ein lineares Modell in Bezug auf die Parameter gefallen, kann man den Anweisungen in Abschnitt 10.1.2 folgen, sonst den Anweisungen im Abschnitt 10.1.4.
Um lineares Fitten zu verstehen, sollte man sich vergegenwärtigen, wie man
ein Polynom exakt durch ![]() -Datenpunkte
-Datenpunkte
![]() legen kann. Man
benötigt dazu im Normalfall ein Polynom
legen kann. Man
benötigt dazu im Normalfall ein Polynom ![]() -ten Grades mit
-ten Grades mit ![]() Koeffizienten. Die Koeffizienten müssen dabei folgendes bestimmtes
Gleichungssystem erfüllen
Koeffizienten. Die Koeffizienten müssen dabei folgendes bestimmtes
Gleichungssystem erfüllen
a=X\y, wobei
Im Falle des Fittens hat man es normalerweise mit einer größeren Anzahl von
Datenpunkten zu tun und möchte in den seltensten Fällen Modellfunktionen mit
der gleichen Anzahl von Parametern verwenden. Damit hat man es mit einem
überbestimmten Gleichungssystem zu tun, dass nicht mehr exakt gelöst werden
kann. In MATLAB kann man für die Lösung eines solchen überbestimmten
Gleichungssystems aber die gleiche Syntax verwenden. Sobald ein
Gleichungssystem überbestimmt ist, löst MATLAB bei Verwendung des Befehls
a=X\y das Gleichungssystem im Sinne des ''Least-Squares''-Verfahrens
entsprechend der Gleichung 10.1.
Die Unterscheidung zwischen linearen und nichtlinearen Modellfunktionen ist
deswegen so wichtig, weil in der numerischen Umsetzung wesentliche
Unterschiede bestehen. Im Fall von linearen Funktionen kann das
Minimierungsproblem in Gleichung 10.1 immer in ein exakt
lösbares lineares Gleichungssystem überführen. Wie man sich leicht überzeugen
kann, erhält man für
![]() aus
aus
![]() das lineare Gleichungssystem
das lineare Gleichungssystem
| (10.13) | ||
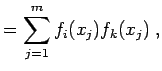 |
(10.14) | |
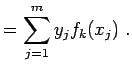 |
(10.15) |
xd = linspace(-pi,pi,9); yd = sin(xd); grad = 5; p1 = polyfit(xd,yd,grad); x = linspace(-pi,pi,500); y1 = polyval(p1,x); subplot(1,2,1);plot(xd,yd,'ro',x,sin(x),'r-',x,y1,'b-'); x = linspace(-2*pi,2*pi,500); y1 = polyval(p1,x); subplot(1,2,2);plot(xd,yd,'ro',x,sin(x),'r-',x,y1,'b-');
![\includegraphics[width=10cm]{appdata/polyfitsin}](img344.gif)
Diese Darstellung demonstriert drei interessante Aspekte:
Will man an diesem Beispiel die Koeffizienten für die geraden Potenzen von vorne herein auf Null setzen, kann man polyfit nicht verwenden und muss sich auf das Lösen von überbestimmten Gleichungssystemen besinnen.
X = [xd(:).^5,xd(:).^3,xd(:)]; b = yd(:); a = X \ b; p2 = zeros(1,grad+1); p2(1:2:end) = a;Hier werden nach Lösen des Gleichungssystems mit
a = X\b die drei
erhaltenen Koeffizienten an den richtigen Stellen im Polynom p2
gespeichert.
Im allgemeinen Fall muss es sich nun nicht um Polynome handeln. Im folgenden
Beispiel soll die Funktion ![]() , die als
, die als
| (10.16) | ||
| (10.17) | ||
| (10.18) |
f1c = 'exp(-0.2*x)'; f2c = 'sin(4*x).*exp(-0.4*x)'; fc = ['a(1)*',f1c,'+a(2)*',f2c]; f1 = inline(f1c,'x'); f2 = inline(f2c,'x'); f = inline(fc,'x','a');Um das lineare Gleichungssystem nun lösen zu können, muss man die Koeffizientenmatrix X und den Inhomegenitätsvektor b definieren und dann die Lösung für die Koeffizienten a bestimmen:
X = [f1(xd(:)),f2(xd(:))]; b = yd(:); a = X\b;Mit diesen Daten kann man nun die Funktionen darstellen.
![\includegraphics[width=10cm]{appdata/fitlinsin}](img352.gif)
| (10.20) | ||
| (10.21) | ||
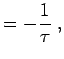 |
(10.22) | |
| (10.23) |
Vorausgesetzt die Zeit- und die Intensitätswerte sind in den Variablen t und I gespeichert, kann man nun wieder das Gleichungssystem aufbauen und lösen. Hier sieht man auch, dass wenn man ein konstantes Glied bestimmen will, die Matrix X einfach eine Reihe mit Einsen enthalten muss:
X = [t(:),ones(size(t(:)))]; b = log(I(:)); a = X\b; tau = -1 / a(1); I0 = exp(a(2));Nach Durchführen des Fits (Lösen des Gleichungssystems) kann man natürlich dann wieder die interessierenden Größen
![\includegraphics[width=10cm]{appdata/radiofit}](img364.gif)
Im Falle einer Modellfunktion, die eine nichtlineare Funktion in den
Modellparametern ist, muss man nun zu anderen Methoden greifen. Als
einfachstes Beispiel soll hier eine Schwingung mit Amplitude ![]() , Frequenz
, Frequenz
![]() und Phase
und Phase ![]() verwendet werden, die durch folgenden Zusammenhang
gegeben ist
verwendet werden, die durch folgenden Zusammenhang
gegeben ist
Für eine Umsetzung des Problems in MATLAB muss man nun eine MATLAB-Funktion oder eine inline-Funktion schreiben, die den funktionalen Zusammenhänge wiedergibt:
fc = 'a(1)*sin(a(2)*t+a(3))'; f = inline(fc,'a','t');Wichtig dabei ist, dass alle Parameter (hier
Der Funktionsaufruf y=f(a,t) muss also für jeden Parametervektor a und jeden Zeitvektor t die Auslenkung y liefern, wobei y die gleiche Größe wie t haben muss.
In diesem Beispiel liegen die Datenpunkte wieder als Vektoren td und yd vor. Im Unterschied zum nichtlinearen Fitten braucht man nun aber auch einen Startwert für die Parameter um MATLAB mitzuteilen, wo man ungefähr die Lösung erwartet. Danach kann man mit dem MATLAB-Programm nlinfit den Fit durchführen. Diese Routine stammt aus dem MATLAB-Statistik Toolbox, ist also beim Grundpaket nicht installiert.
as = [0.8,1,0.2]; af = nlinfit(td,yd,f,as) t = linspace(-4*pi,4*pi,1000); y = f(af,t);
Damit kann man sich dann mit dem Zeitvektor t die Modellfunktion berechnen und zusammen mit den Daten darstellen.
![\includegraphics[width=10cm]{appdata/nonlinfit1}](img368.gif)
Warum braucht man nun einen Startwert. Im Unterschied zum linearen Fitten, wo das zugehörige Gleichungssystem immer eine eindeutige Lösung besitzt, die direkt ermittelt werden kann, benötigt man hier ein iteratives Verfahren. Dabei wird ausgehend von einem Startwert das Minimum einer Funktion gesucht, in dem man sich Schritt für Schritt dem Minimum nähert. Dazu gibt es viele Möglichkeiten (z.B.: Gauss-Newton). Entscheidend ist also der Unterschied, das es kein direktes Verfahren gibt um die Lösung zu finden. Nichtlineare Probleme haben dazu auch häufig mehrere (oft viele) ''lokale'' Minima, interessiert ist man aber am so genannten ''globalen'' Minimum, welches die ''bestmögliche'' Lösung des Problems darstellt. Daher ist eine gute Wahl des Startwertes meist eine essentielle Vorleistung für eine gute Lösung. Meist findet man diese durch ''clevere'' Betrachtung der Daten.
Als weiteres Beispiel soll hier die Funktion aus Gleichung 10.16 verallgemeinert werden, indem alle Parameter veränderlich gemacht werden,
| (10.25) | ||
| (10.26) | ||
| (10.27) |
Dies ist nun ein nichtlineares Problem in ![]() mit folgender Umsetzung in
MATLAB:
mit folgender Umsetzung in
MATLAB:
fc = 'a(1)*exp(-a(3)*x) + a(2)*sin(a(4)*x).*exp(-a(5)*x)'; fa = inline(fc,'a','x');
Unter der Voraussetzung, dass die Daten wieder in xd und yd zur Verfügung stehen, kann man die Lösung folgendermaßen finden
as1 = [2,1,1,2,1]; af1 = nlinfit(xd,yd,fa,as1)
Die Darstellung der Daten, des Ergebnisses und der Resultate von zwei Startwerten kann man in folgender Graphik sehen:
![\includegraphics[width=10cm]{appdata/nonlinfit}](img371.gif)
Die Standard MATLAB-Funktion für das suchen von Minima ist die Routine
fminsearch. Um diese beim vorliegenden Problem verwenden zu können,
muss man eine Funktion programmieren, die den Skalarwert ![]() der
Gleichung 10.1 zurück gibt. Diese Funktion muss also die Summe
der Abstandsquadrate an allen Datenpunkten berechnen und benötigt dafür den
Parametervektor a und die Daten xd und yd. Am Beispiel der
letzten Funktion kann das so aussehen:
der
Gleichung 10.1 zurück gibt. Diese Funktion muss also die Summe
der Abstandsquadrate an allen Datenpunkten berechnen und benötigt dafür den
Parametervektor a und die Daten xd und yd. Am Beispiel der
letzten Funktion kann das so aussehen:
function q = lqfunc(a,xd,yd) y = a(1)*exp(-a(3)*xd) + a(2)*sin(a(4)*xd).*exp(-a(5)*xd); q = sum((y-yd).^2);Wichtig ist also der Punkt, dass hier jeweils nur ein skalarer Wert, nämlich der Wert der zu minimierenden Funktion, zurückgegeben wird. Diese Funktion wird nun an fminsearch zusammen mit Startwerten übergeben
af3 = fminsearch(@lqfunc,as1,[],xd,yd)und liefert die ''besten'' Parameter. An Stelle von
[] kann man
Optionen übergeben (siehe Hilfe zu fminsearch). Die Datenvektoren
xd und yd werden von fminsearch
an die Funktion lqfunc weitergegeben. Dieses Beispiel zeigt somit nochmals, dass
eigentlich die Funktion 10.1 minimiert wird, und dass dies
dann zur besten Annäherung der Modellfunktion an die Daten führt.
Winfried Kernbichler 2005-04-26