12.5 Logische Indizierung

Ziel:

Ziel der Übung ist die Verwendung der logischen Indizierung in MATLAB, wie sie im Abschnitt 3.6.1 besprochen wird.

Anzufertigen sind die MATLAB-Funktionen quadgl, quadgleval, rangetest und ein MATLAB-Skript ueblogical. Die Funktionen enthalten die Lösungen für alle Unterbeispiele und das Skript ist eine einfache Testroutine für die Funktionen.

Voraussetzung:

Der Zugriff auf Teile von Arrays wird wir im Abschnitt 3.6 erläutert, wobei man im Abschnitt 3.6.2 ausführliche Beispiele findet. Teile davon waren Bestandteil der letzten Übung. Für die heutige Übung benötigt man zusätzlich Kenntnisse über die logische Indizierung aus dem Abschnitt 3.6.1. Auch dazu gibt es Beispiele in 3.6.2.3.

Die vorbereiteten Programme für die Übung können mit dem Befehl !uebungsdaten geladen werden. Die Übungsnummer ist 5. Die Programme, die zur Verfügung stehen sind:

issamesize zum Größenvergleich von Arrays
showmat zur graphischen Darstellung von Arrays
showmata zur graphischen Darstellung von Arrays in einem Bild

Benötigt wird auch Basiswissen über Logische Operatoren.

Eine quadratische Gleichung der Form

$\displaystyle ax^2 + bx + c = 0 \qquad a,b,c \in \mathbb{R}$

(12.1)

hat folgende Lösungen

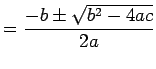$\displaystyle x_{1,2}$	$\displaystyle = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$	$\displaystyle a \neq 0$	(12.2)
$\displaystyle x_{1}$	$\displaystyle = -c/b$	$\displaystyle a = 0 \wedge b \neq 0$
$\displaystyle x_{1}$	$\displaystyle = 0$ triviale Lösung	$\displaystyle a = 0 \wedge b = 0 \wedge c = 0$

Der Ausdruck

$\displaystyle D=b^2 - 4ac$

(12.3)

wird dabei als Diskriminante bezeichnet. Im Falle $a \neq 0$ entscheidet sein Wert, ob es zwei reelle Lösungen, eine reelle Doppellösung, oder zwei konjugiert komplexe Lösungen gibt. Für den Fall $a = 0 \wedge b = 0 \wedge c \neq 0$ gibt es keine Lösung.

Zu erstellen ist nun ein Unterprogramm
[x1,x2]=quadgl(a,b,c)
welches 12.1 löst, wobei die Koeffizienten , und beliebige Felder mit reellen Zahlen sein können. D.h. die Gleichung soll simultan für mehrere Werte der Koeffizienten gelöst werden, wobei die Ergebnisse in den Feldern und gespeichert werden sollen. Zu verwenden sind dabei die Lösungen aus 12.2, wobei dort wo keine Lösungen existieren, der Wert NaN (entspricht: Not A Number) verwendet werden soll. Dort wo beliebige Lösungen erlaubt sind, soll für die triviale Lösung 0 verwendet werden.

Dazu notwendig ist Folgendes:

Zu einem guten Programm gehört die Überprüfung der Eingabeparameter:
Die Anzahl der Eingabeparameter (7.1.6) sollte hier immer drei sein (keine Defaultwerte), ansonsten sollte eine Fehlermitteilung geschrieben werden (error).
Außerdem sollte mit Hilfe der Befehle issamesize (wurde bereitgestellt), isnumeric und isreal überprüft werden, ob die Koeffizientenfelder gleich groß sind, ob sie Zahlen sind und, ob sie reelle Zahlen enthalten. Hilfe zu den Befehlen bekommt man z.B. mit help issamesize oder auch im Abschnitt 7.1.4. Falls die Bedingungen nicht erfüllt sind, sollte wieder eine Fehlermitteilung geschrieben werden.
Die Lösung des Problems ist mit Hilfe der logischen Indizierung relativ einfach. Die beste Strategie ist für x1, x2 und D Felder der Größe von a anzulegen und mit dem Wert nan zu belegen.
Danach kann man drei logische Felder entsprechend der drei logischen Bedingungen in 12.2 erzeugen und diese dann auf beiden Seiten der Zuweisungen verwenden. Damit ist sichergestellt, dass die jeweiligen Berechnungen nur durchgeführt werden, wenn die entsprechende Bedingung erfüllt ist.
Zwei Dinge sollte man sich überlegen: Warum ist es besser die Diskriminante nur einmal zu berechnen und dann in der Formel für $x_{1,2}$ zu verwenden? Warum muss man in MATLAB keine Unterscheidung treffen, ob der Wert größer oder kleiner Null ist?

Schreiben Sie eine kleine MATLAB-Funktion
[r1,r2] = quadgleval(a,b,c,x1,x2)
welche die Resultate der linken Seite von 12.1 berechnet. Damit kann man dann später beurteilen, wie nahe diese bei Null liegen. Überlegen Sie wieder welche Operatoren Sie verwenden müssen. Mit nan kann man normal rechnen, wobei jede arithmetische Operation mit nan wieder nan ergibt.

Zum Testen der Funktionen benötigen Sie ein MATLAB-Skript
ueblogical
wobei mit input die Variablen n (Größe der Matrizen, Default 15), rmin (Minimale Zufallszahl, Default 2), rmax (Maximale Zufallszahl, Default 5), delay (Verzögerungszeit, Default 2), und graph (Graphikoutput, Default 'y') zugewiesen werden. Für das Setzen der Defaultwerte empfiehlt sich die Verwendung von isempty.

Erzeugen Sie nun die drei $n \times n$ -Felder a, b und c mit gleichverteilten Zufallszahlen zwischen $r_{min}$ und $r_{max}$ . Der Befehl rand(n) liefert dabei gleichverteilte Zufallszahlen im Interval zwischen 0 und . Die Anpassung an das Intervall zwischen $r_{min}$ und $r_{max}$ erfolgt dabei durch eine Skalierung (Multiplikation) und Verschiebung (Addition).

Setzen Sie danach die mittlere Spalte von a und die mittlere Zeile von b auf den Wert Null. Wenn es keine mittlere Zeile oder Spalte gibt (gerade Anzahl), dann nehmen Sie die Spalte (Zeile) mit dem nächsthöheren Index.

Rufen Sie quadgl und danach mit den Resultaten quadgleval auf. Die Resultate können Sie graphisch darstellen:

 showmata(real(x1),real(x2)) % Realteile
 pause(delay)                % Verzögerung
 showmata(imag(x1),imag(x2)) % Imaginärteile
 pause(delay)                
 showmata(abs(r1),abs(r2))   % Absolutwerte der rechten Seite
 pause(delay)

Die Befehle real, imag und abs berechnen den Realteil, den Imaginärteil und den Absolutwert.

Sie sollten nun die Resultate in einer Farbcodierung sehen, wobei weisse Bereiche nan symbolisieren. Wegen numerischer Ungenauigkeiten ergeben sich für die Werte auf der rechten Seite nicht nur Null, sondern auch kleine Werte im Bereich $10^{-15}$ .

Zählen Sie nun für die beiden Felder ar1=abs(r1) und ar2 die Anzahl der Werte mit exakter Null, mit nan (isnan). Dabei summiert man immer über alle Werte (Doppelpunkt) in den entsprechenden logischen Arrays.

Außerdem soll man in einer for-Schleife jeweils alle Werte $10^{k} \le \vert r_{1,2}\vert < 10^{k+1}$ zählen, wobei k von bis laufen soll.

Geben Sie all diese Summen formatiert aus und überlegen Sie, ob sie stimmen können. Es sollten eine gewisse Anzahl von Nullen, von nan und sonst eher kleine Werte vorkommen. Kommen zu große Werte vor, ist sicher etwas falsch.

Schreiben Sie eine Funktion
[m,count] = rangetest(m,b,e)
wobei m eine beliebige Matrix, b ein Vektor der Länge 2 und e ein Vektor der Länge 3 ist.

Für die Output-Matrix m soll Folgendes gelten

$\displaystyle m_{i,j}$	$\displaystyle = e_1$	$\displaystyle m_{i,j} < b_1$	(12.4)
$\displaystyle m_{i,j}$	$\displaystyle = e_2$	$\displaystyle b_1 \le m_{i,j} \le b_2$	(12.5)
$\displaystyle m_{i,j}$	$\displaystyle = e_3$	$\displaystyle m_{i,j} > b_2 \; .$	(12.6)

Der Vektor count (Länge 3) soll die Anzahl der jeweiligen Ersetzungen enthalten.

Sie können auf alle Überprüfungen und auf das Setzen von Defaultwerten verzichten, wichtig ist nur die Funktionalität der MATLAB-Funktion. Die gesamte Aufgabe soll wieder ohne if und for unter Verwendung der logischen Indizierung funktionieren.

Ergänzen Sie das MATLAB-Skript
ueblogical
um folgende Teile. Erzeugen Sie eine weitere $n \times n$ -Matrix m mit gleichverteilten Zufallszahlen zwischen $r_{min}$ und $r_{max}$ . Erzeugen Sie einen Vektor b mit zwei Einträgen, der den Bereich zwischen $r_{min}$ und $r_{max}$ in drei gleiche Teile teilt. Als Vektor e verwenden Sie [-1,0,1].

Stellen Sie die Matrix vor und nach der Ersetzung graphisch dar. Die Bilder sollten dabei ungefähr so aussehen.

$\includegraphics[width=0.45\textwidth]{appdata/rangetestv}$ $\includegraphics[width=0.45\textwidth]{appdata/rangetestn}$

Geben Sie die Werte von count formatiert aus und überprüfen Sie, ob die Gesamtzahl der Ersetzungen gleich der Anzahl der Elemente in m ist.

Winfried Kernbichler 2005-04-26