Next: 12.9 Lineare Gleichungssysteme Up: 12. Übungsbeispiele Previous: 12.7 Kurvendiskussion Contents
| (12.19) | ||
| (12.20) |
| (12.21) | ||
| (12.22) |
Die Gestaltung der Graphik und die Auswahl der Defaultwerte ist Ihnen überlassen. Wählen Sie sie so, dass man eine interessante Animation sieht.
Verwenden Sie dabei zur Erstellung der Graphik die Befehle figure, axes, line. Diese (alle) Graphikbefehle haben als Rückgabewert einen sogenannten Graphik-Handle, der einen weiteren Zugriff auf diese Graphikobjekte ermöglicht:
fh = figure; clf reset; % loescht alle Children, Eigenschaften set(fh,'Color',[1,1,0.8]); set(fh,.........)Damit kann man alle Eigenschaften von Graphikobjekten verändern. Dazu kann man sich im helpbrowser die Seite ''Handle Graphics Property Browser'' ansehen, die für alle Graphikobjekte Eigenschaften und mögliche Werte angibt. Eine Einführung zu diesem Konzept gibt es im Abschnitt 11.1. Verwenden Sie dieses Konzept um einige Einstellungen für figure und axes vorzunehmen.
Das gleiche Konzept wird zur Animation von Graphiken verwendet. Dabei tauscht man in einer Schleife (while) z.B. die Daten einer Linie (eines Punktes) aus:
lh = line(x,y,'LineStyle','none');
set(lh,'Marker','o')
% MarkerSize, MarkerEdgeColor, MarkerFaceColor, ....
t = t_anf;
while t <= t_end
t = t + delta_t;
x = ....
y = ....
set(lh,'XData',x,'YData',y);
drawnow;
pause( ........... )
end
Die Animation erfolgt also durch Austauschen der x- und y-Werte. Der Befehl
drawnow
stellt sicher, dass zu diesem Zeitpunkt ein Update der
graphischen Ausgabe (Schirm) stattfindet. MATLAB merkt sich ansonsten
Graphikbefehle in einer Art Pipeline und optimiert die Umsetzung.
Damit sollte es Ihnen möglich sein, dass sich die Punkte über die Graphik bewegen. Wichtig dabei ist, dass man mit den Eigenschaften XLim bzw. YLim die Achsenlimits gleich am Anfang in entsprechender Größe einstellt, damit sich diese nicht bei der Bewegung mitändern. In manchen Fällen, will man das Achsensystem so gestalten, das es sich über die gesamte Graphik ausdehnt und unsichtbar bleibt. Dies erreicht man mit Hilfe der Eigenschaften Position und Visible.
Ein wichtiger Punkt ist auch die oft notwendige Verzögerung der Graphikausgabe mit dem Befehl pause, da sonst oft die Animationen zu schnell abläuft. Dabei kann man mit den Befehlen clock und etime die gegenwärtige Zeit bzw. die verstrichene Zeit berechnen und damit ein vernünftiges Argument für pause berechnen:
t_0 = clock; ...... t_elapsed = etime(clock,t_0);Wenn dieser Teil funktioniert, ergänzen Sie die Ausgabe um ''Schweife'' beschränkter Länge, die jeder Punkt nach sich zieht. Diese stellen quasi eine Spur dar. Dafür führt man weitere zwei Linien ein, die nun nicht mehr nur aus einem Punkt sondern aus einer Reihe von Punkten bestehen. Dies kann man dadurch erreichen, dass man an die entsprechenden Vektoren bei jedem Zeitschritt vorne den neuen Punkt anfügt. Wenn die Vektoren die gewünschte Länge überschreiten, schneidet man den hinteren Bereich ab und animiert dann unter Verwendung von XData und YData diese Kurven.
| ... | Konstante, die aber von der Wellenlänge des Lichtes abhängt | |
| ... | Spannung an einem Kondensator, der das elektrische Feld erzeugt |
Die Datei kerrtab-pu.dat
enthält folgende Daten:
Achtung: Der Befehl polyfit legt die Ausgleichsgerade nicht unbedingt durch
den Ursprung. Wenn man das erreichen will, darf man für die Gerade nur die
Formel ![]() verwenden. Die Steigung
verwenden. Die Steigung ![]() ergibt sich dann aus
ergibt sich dann aus
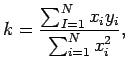
Winfried Kernbichler 2005-04-26