Subsections
12.9 Lineare Gleichungssysteme
- Ziel:
- In dieser Übungseinheit soll der Umgang mit linearen
Gleichungssystemen gelernt werden.
Anzufertigen sind die MATLAB Script-Files
ueblinear.m und kegelgl.m.
- Voraussetzung:
- Grundlegendes Wissen über lineare Algebra, wie sie im
Kapitel 5 besprochen werden.
12.9.1 Netzwerk
Gegeben ist ein Netzwerk mit ohmschen Widerständen und Spannungsquellen
(Abb. 12.1).
Figure 12.1:
Netzwerk mit 4 ohmschen Widerständen und 2 Spannungsquellen.
|
|
Die sich einstellenden Ströme kann man bequem über die Kirchhoffschen
Regeln bestimmen:
- a)
- Knotenregel: An jedem Knoten ist de Summe der
einfließenden Ströme gleich der Summe der ausfließenden Ströme. In
unserem Beispiel heißt das:
- Knoten P:
-
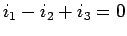 |
(12.24) |
- Knoten Q:
-
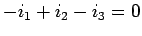 |
(12.25) |
In diesem Fall sind das äquivalente Gleichungen, wovon nur eine
benötigt wird.
- b)
- Schleifenregel: In jeder Schleife ist die Summe der
Spannungsabfälle gleich der Summe der Spannungsquellen.
- Rechte Schleife:
-
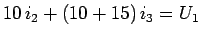 |
(12.26) |
- Linke Schleife:
-
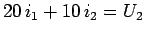 |
(12.27) |
Wir können dieses lineare Gleichungssystem in Matrixform schreiben.
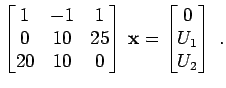 |
(12.28) |
Lösen Sie diese Gleichungssystem für
- a)
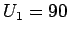 ,
, 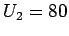
- b)
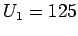 ,
, 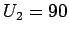
- c)
- Kann man dieses Gleichungssystem auch für mehrere Vektoren
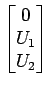 |
(12.29) |
zugleich lösen? Lösen Sie das System für die Vektoren aus a), b) und für
den Vektor mit 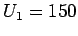 ,
, 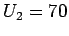 mit einem Befehl.
mit einem Befehl.
Überlegen Sie, wie Sie dafür die Spaltenvektoren in einer Matrix anordnen
müssen.
12.9.2 Vertauschung
Gegeben sind eine Matrix 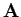 und ein Vektor
und ein Vektor 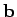 :
:
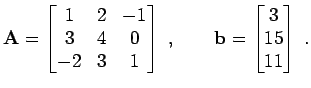 |
(12.30) |
Lösen Sie
- a)
-
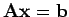
- b)
-
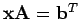
Sind die Ergebnisse gleich?
12.9.3 Diagonalmatrix
Die Matrix 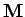 ist eine
ist eine
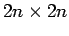 Matrix, deren Hauptdiagonale aus
Einsen besteht und deren beiden Nebendiagonalen mit
Matrix, deren Hauptdiagonale aus
Einsen besteht und deren beiden Nebendiagonalen mit 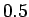 gefüllt sind
gefüllt sind
 |
(12.31) |
Der Vektor 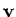 ist durch
ist durch
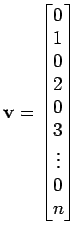 |
(12.32) |
gegeben. Erstellen Sie die Matrix 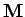 mit Hilfe der Befehle
eye
und diag, und den Vektor
mit Hilfe der Befehle
eye
und diag, und den Vektor 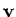 mit Hilfe des
Befehls zeros
und der Doppelpunk Notation.
mit Hilfe des
Befehls zeros
und der Doppelpunk Notation.
- a)
- Berechnen Sie die Lösung der Gleichung
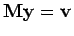 für
für 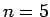 .
.
- b)
- Machen Sie die Probe
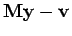 . Kommt tatsächlich der
Nullvektor heraus? Überlegen Sie sich, woher die Abweichungen herrühren!
. Kommt tatsächlich der
Nullvektor heraus? Überlegen Sie sich, woher die Abweichungen herrühren!
Im letzten Punkt haben wir gesehen, dass durch die endliche Genauigkeit der
Zahlen während der Berechnung Rundungsfehler entstehen.
Daher macht
eine Probe in der Form
if all( (M*y - v) == 0 )
disp('Probe bestanden.');
else
disp('Probe nicht bestanden.');
end
keinen Sinn!
Die einzige Möglichkeit, die man hat, ist auf beinahe Gleichheit zu
testen. Dazu bietet sich der absolute oder der relative Fehler
an. Wir wollen hier den absoluten Fehler verwenden.
error_limit = 1.0e-8;
if all( abs(M*y - v) < error_limit )
disp('Probe bestanden.');
else
disp('Probe nicht bestanden.');
end
- c)
- Versuchen Sie diese Programmzeilen zu verstehen!!! Führen Sie
auf diese Weise die Probe durch.
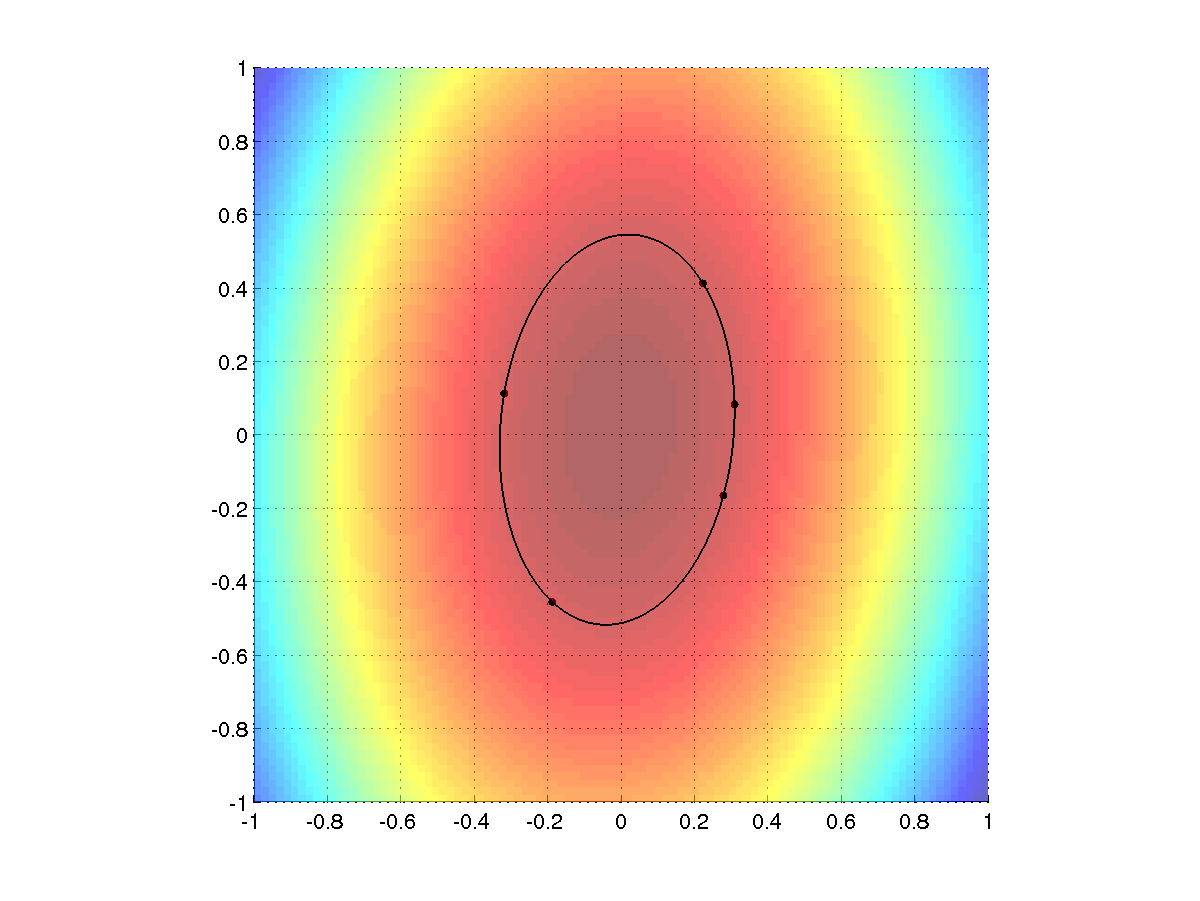
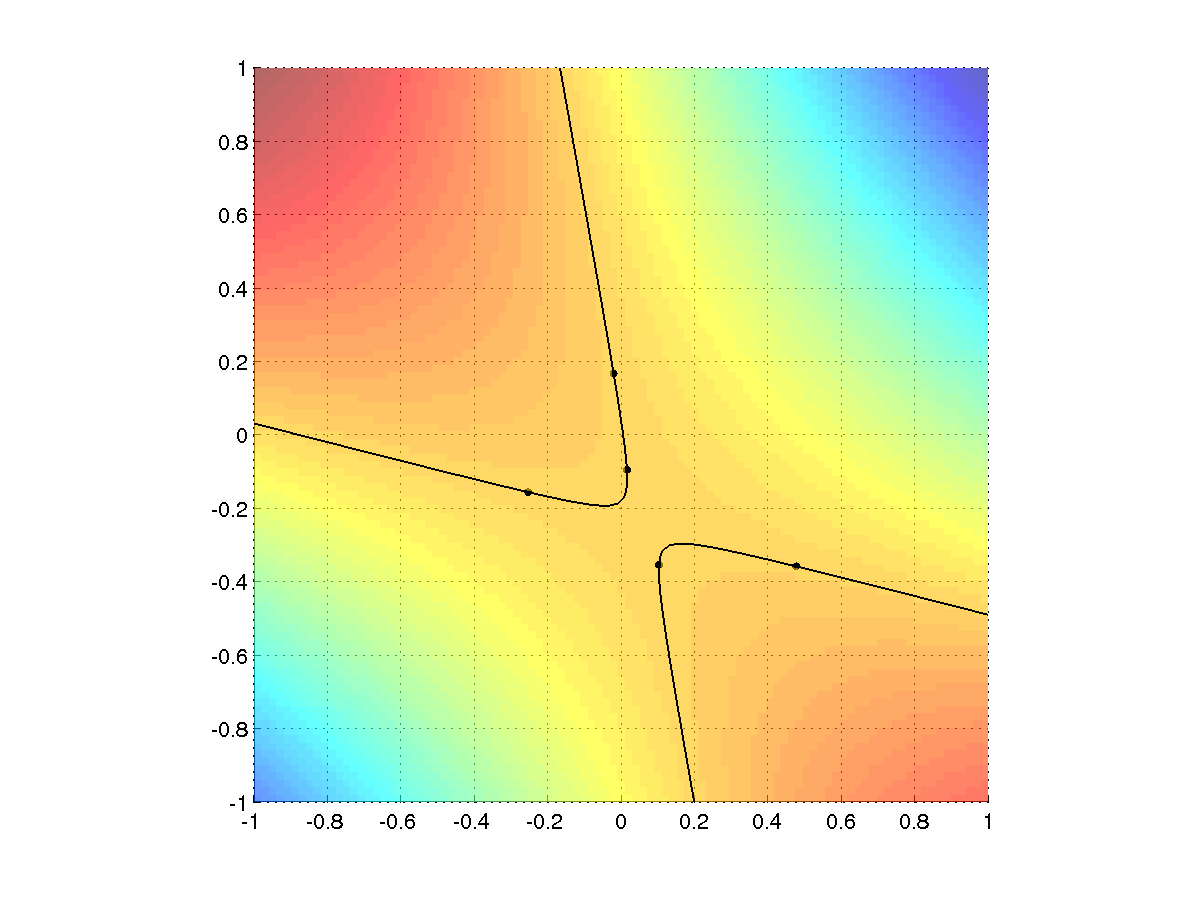
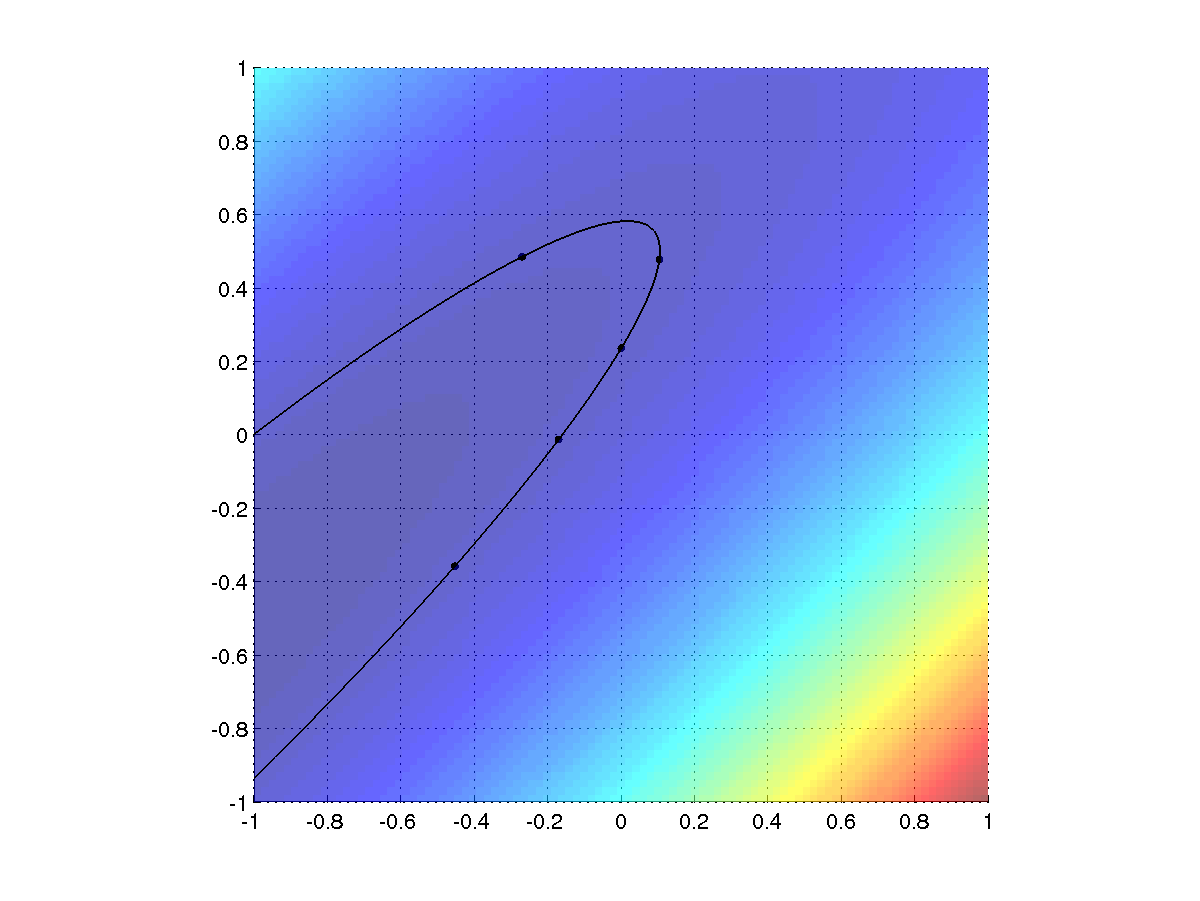
12.9.4 Kegelschnitt
Als verallgemeinerte quadratische Formen bezeichnet man Funktionen folgender
Form:
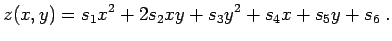 |
(12.33) |
Schnitte einer solchen Fläche mit einer Ebene (z.B., 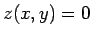 ) bezeichnet
man als Kegelschnitte (Ellipse, Kreis, Hyperbel, Parabel) bzw. als entartete
Kegelschnitte (Gerade, Geradenpaar, Punkt).
) bezeichnet
man als Kegelschnitte (Ellipse, Kreis, Hyperbel, Parabel) bzw. als entartete
Kegelschnitte (Gerade, Geradenpaar, Punkt).
Bei bekannten Datenpunkten 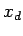 und
und 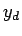 kann man
kann man
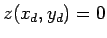 als
lineares Gleichungssystem für
als
lineares Gleichungssystem für 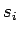 auffassen
auffassen
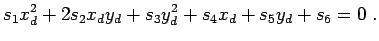 |
(12.34) |
In dieser Form ist es ein homogenes Gleichungssystem, das immer die triviale
Lösung 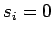 liefern würde. Man kann sich aber helfen und einen der
Koeffizienten
liefern würde. Man kann sich aber helfen und einen der
Koeffizienten 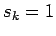 setzen und den entsprechenden Term auf die rechte Seite
bringen. Wählt man z.B. den dritten Term
setzen und den entsprechenden Term auf die rechte Seite
bringen. Wählt man z.B. den dritten Term 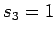 lautet die das inhomogene
Gleichungssystem
lautet die das inhomogene
Gleichungssystem
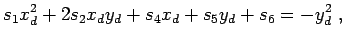 |
(12.35) |
welches nun die Form
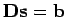 hat und mit MATLAB gelöst
werden kann. Da es nun fünf unbestimmte Koeffizienten gibt, genügen fünf
Datenpunkte
hat und mit MATLAB gelöst
werden kann. Da es nun fünf unbestimmte Koeffizienten gibt, genügen fünf
Datenpunkte 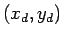 , um den Kegelschnitt genau zu bestimmen.
, um den Kegelschnitt genau zu bestimmen.
Gehen Sie nun im Skript kegelgl.m folgendermaßen vor:
- Erzeugen Sie zwei
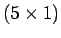 -Vektoren xd und yd mit
gleichverteilten Zufallszahlen zwischen
-Vektoren xd und yd mit
gleichverteilten Zufallszahlen zwischen 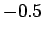 und
und 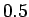 (rand).
(rand).
- Erzeugen Sie mit Hilfe dieser Vektoren die Hilfsmatrix
wobei
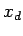 ,
, 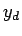 und
und 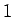 jeweils Spaltenvektoren gleicher Länge sein
müssen.
jeweils Spaltenvektoren gleicher Länge sein
müssen.
- Wählen Sie den Index einer Spalte aus, die auf die rechte Seite des
Gleichungssystems gebracht werden soll und erzeugen Sie damit die Matrix
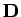 und den Inhomogenitätsvektor
und den Inhomogenitätsvektor 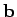 . Diese Auswahl kann man am
leichtesten mit Hilfe eines logischen Vektors (z.B.:
. Diese Auswahl kann man am
leichtesten mit Hilfe eines logischen Vektors (z.B.:
![$ [0,0,1,0,0,0]$](img675.gif) ) und
seiner Negation treffen (logische Indizierung).
) und
seiner Negation treffen (logische Indizierung).
- Lösen Sie das entsprechende Gleichungssytem
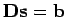 und
fügen im so erhaltenen
und
fügen im so erhaltenen 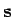 an der richtigen Stelle
an der richtigen Stelle 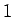 ein (logische
Indizierung). Damit ist das Problem gelöst und das Ergebnis muss nur noch
visualisiert werden.
ein (logische
Indizierung). Damit ist das Problem gelöst und das Ergebnis muss nur noch
visualisiert werden.
- Erzeugen Sie dafür Vektoren
 und
und 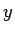 zwischen
zwischen 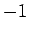 und
und 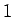 mit
circa
mit
circa 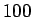 Punkten. Alle Kombinationen von
Punkten. Alle Kombinationen von  - und
- und 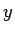 -Werten kann man
mit dem Befehl meshgrid
erzeugen und erhält damit die Matrizen
-Werten kann man
mit dem Befehl meshgrid
erzeugen und erhält damit die Matrizen
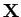 und
und 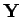 . Durch Auswertung von Gleichung 12.33
für diese Matrizen erhält man
. Durch Auswertung von Gleichung 12.33
für diese Matrizen erhält man
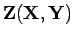 .
.
- Diese Fläche kann man mit dem Befehl surf
graphisch
Darstellen. Die Farbe repräsentiert den Wert der Funktion und man kann
von Oben auf die Fläche schauen (view(2)). Verwendet man
eine Handle für diese ''Surface'', kann man die EdgeColor auf none setzen um die störenden schwarzen Linien zu beseitigen.
- Nun kann man in der gleichen Zeichnung die Datenpunkte einzeichen
(line) und den erhaltenen Kegelschnitt als Höhenschichtlinie
zeichnen. Dafür gibt es in MATLAB den Befehl
contour(X,Y,Z). In dieser Form wählt MATLAB die
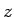 -Werte für die Höhenschichtlinien automatisch aus. Man kann aber auch
einen weiteren Vektor v mit gewünschten Höhenwerten übergeben:
-Werte für die Höhenschichtlinien automatisch aus. Man kann aber auch
einen weiteren Vektor v mit gewünschten Höhenwerten übergeben:
v = [0,0]; contour(X,Y,Z,v);
Will man nur einen Höhenwert muss man ihn seltsamerweise zweimal
übergeben. Vergessen Sie auch nicht die Verwendung von hold.
- Damit sollten nun die Höhe von
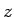 in Farbe dargestellt sein, die
Datenpunkte und der Kegelschnitt als Höhenschichtlinie eingezeichnet
sein. Der Kegelschnitt sollte genau durch die fünf Datenpunkte gehen und
entlang einer gleichen Farbe verlaufen.
in Farbe dargestellt sein, die
Datenpunkte und der Kegelschnitt als Höhenschichtlinie eingezeichnet
sein. Der Kegelschnitt sollte genau durch die fünf Datenpunkte gehen und
entlang einer gleichen Farbe verlaufen.
Winfried Kernbichler
2005-04-26
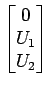
![]() und ein Vektor
und ein Vektor ![]() :
:
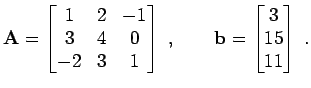
![]() ist eine
ist eine
![]() Matrix, deren Hauptdiagonale aus
Einsen besteht und deren beiden Nebendiagonalen mit
Matrix, deren Hauptdiagonale aus
Einsen besteht und deren beiden Nebendiagonalen mit ![]() gefüllt sind
gefüllt sind

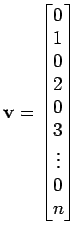
![]() und
und ![]() kann man
kann man
![]() als
lineares Gleichungssystem für
als
lineares Gleichungssystem für ![]() auffassen
auffassen