5. Operatoren für Matrizen - Lineare Algebra

Als Matrizen bezeichnet man eine rechteckige Anordnung von Zahlen (oder Variablen). Im Unterschied zu den Feldern (Arrays), die exakt das gleiche Aussehen haben, werden hier Matrizen als Konstrukte der linearen Algebra aufgefasst, für die natürlich andere Regeln in Bezug auf für Multiplikation und Division gelten.

Eine Matrix 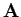${\bf A}$ kann geschrieben werden als

$${\bf A}= \begin{bmatrix}a_{11} & a_{12} & a_{13} & a_{14} & \dots... ...m1} & a_{m2} & a_{m3} & a_{m4} & \dots & a_{mn} \end{bmatrix} = [a_{jk}]\; .$$ (5.1)

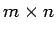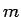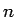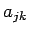Dies ist eine $m \times n$ Matrix mit $m$ Zeilen (rows) and $n$ Spalten (columns). Die einzelnen Elemente werden in der Mathematik mit Hilfe von Indizes $a_{jk}$ bezeichnet, in MATLAB lautet die Schreibweise A(j,k). Die Matrix 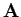${\bf A}$ ist 2-dimensional, es gibt jedoch keine Beschränkung in der Anzahl der Dimensionen. Die beiden MATLAB Befehle ndims und size geben die jeweilige Dimension der Matrix und die Größe in jeder Dimension. Einige Befehle und die zugrundeliegenden Konzepte (z.B.: Transponieren) sind aber nur für 2-dim Matrizen definiert.

Spezielle zweidimensionale Matrizen sind:

Spaltenvektor, column vector:

Matrix mit nur einer Spalte,

$${\bf a}= \begin{bmatrix}a_{11} a_{21} a_{31} \end{bmatrix} = \begin{bmatrix}a_{1} a_{2} a_{3} \end{bmatrix} = [a_{j}]\; .$$ (5.2)

Die Eingabe in MATLAB erfolgt mit a=[1;2;3] oder a=[1,2,3].'. Die Anzahl der Dimensionen ist 2, der Befehl size liefert [3 1].

Zeilenvektor, row vector:

Matrix mit nur einer Zeile,

$${\bf b}=\begin{bmatrix}b_{11} \; b_{12} \; b_{13} \end{bmatrix} = \begin{bmatrix}b_{1} \; b_{2} \; b_{3} \end{bmatrix} = [b_{j}]\; .$$ (5.3)

Die Eingabe in MATLAB erfolgt mit b=[1,2,3]. Die Anzahl der Dimensionen ist 2, der Befehl size liefert [1 3].

Skalar, scalar:

Matrize reduziert auf eine einzige Zahl,

$$s = {\bf s}= s_{11} = s_{1} = [s_{j}]\; .$$ (5.4)

Die Anzahl der Dimensionen ist auch hier 2, der Befehl size liefert [1 1].