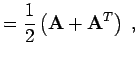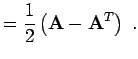5.1 Transponieren einer Matrix
Es erweist sich als praktisch, die Transponierte einer Matrix zu
definieren. Die transponierte Matrix
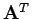 einer
einer
 Matrix
Matrix
![$ {\bf A}= [a_{jk}]$](img162.gif) ist eine
ist eine
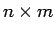 Matrix, wobei die Zeilen in Spalten und die
Spalten in Zeilen verwandelt werden,
Matrix, wobei die Zeilen in Spalten und die
Spalten in Zeilen verwandelt werden,
![$\displaystyle {\bf A}^{T}= [a_{kj}]\; .$](img164.gif) |
(5.5) |
Mit Hilfe der transponierten Matrix können zwei Klassen von reellen
quadratischen Matrizen definiert werden:
- Symmetrische Matrix:
- Für eine symmetrische Matrix gilt
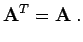 |
(5.6) |
- Schiefsymmetrische Matrix:
- Für eine schiefsymmetrische Matrix gilt
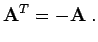 |
(5.7) |
- Zerlegung:
- Jede quadratische Matrix (
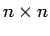 ) lässt sich in eine
Summe aus einer symmetrischen und einer schiefsymmetrischen Matrix
zerlegen,
) lässt sich in eine
Summe aus einer symmetrischen und einer schiefsymmetrischen Matrix
zerlegen,
In MATLAB steht zum Transponieren der Operator .'
oder der Befehl
transpose
zur Verfügung.
Winfried Kernbichler
2005-04-26