5.2 Addition und Subtraktion von Matrizen
Diese beiden Operationen existieren nur ''elementweise'', d.h. es gibt keinen
Unterschied zwischen Matrix- und Array-Operationen
![$\displaystyle {\bf C}= {\bf A}\pm {\bf B}\; \Longrightarrow \; [c_{jk}]= [a_{jk}]\pm [b_{jk}]\; ,$](img174.gif) |
(5.11) |
und daher ist die Defintion von .+ und .- Operatoren nicht notwendig.
- Voraussetzung:
- Gleiche Dimension und gleiche Größe von
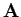 und
und 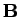 .
.
- Ausnahme:
- A oder B ist ein Skalar, dann wird die skalare Größe zu
allen Elementen addiert (oder von allen subtrahiert).
- Beispiele:
- Mit
![$ {\bf A}= [1 \; 2 \; 3]$](img176.gif) und
und
![$ {\bf B}=[4 \; 5 \; 6]$](img177.gif) ergibt sich,
ergibt sich,
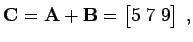 |
(5.12) |
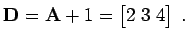 |
(5.13) |
- Fehler:
- Die Rechnung
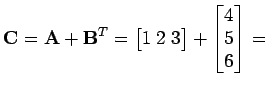 Error Error |
(5.14) |
ergibt natürlich eine Fehlermitteilung.
Winfried Kernbichler
2005-04-26