5.6 Spezielle Matrizen

Für die Beschreibung der Matrix Division beschränken wir uns vorerst auf quadratische Matrizen ( 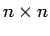$n \times n$). Dafür benötigen wir zuerst die Definition der Einheitsmatrix

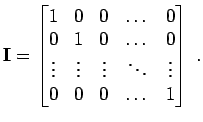$${\bf I}= \begin{bmatrix}1 & 0 & 0 & \dots & 0 0 & 1 & 0 & \dot... ...& \vdots & \vdots & \ddots & \vdots 0 & 0 & 0 & \dots & 1 \end{bmatrix} \; .$$ (5.27)

Für die Einheitsmatrix gilt

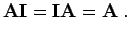$${\bf A}{\bf I}= {\bf I}{\bf A}= {\bf A}\; .$$ (5.28)

In MATLAB steht für die Erzeugung der Befehl eye (zB. eye(3)) zur Verfügung.

Die inverse Matrix ist definiert durch

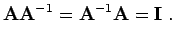$${\bf A}{\bf A}^{-1} = {\bf A}^{-1} {\bf A}= {\bf I}\; .$$ (5.29)

Eine Matrix für die

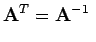$${\bf A}^{T}= {\bf A}^{-1} \;$$ (5.30)

gilt, wird als orthogonale Matrix bezeichnet.

In MATLAB gibt es zur Berechnung der inversen Matrix den Befehl inv(A).