Subsections
12.10 Lineares Fitten
- Ziel:
- Es soll das Fitten von Polynomen durch eine gegebene Datenmenge
erlernt werden.
- Voraussetzung:
- Speichern Sie die Datei
polydat.dat
in Ihrem MATLAB-Directory ab (Skript:
uebungsdaten, Übung 10). Damit bekommen Sie auch eine Reihe von Datenfiles
für Kegelschnitte, die alle mit kschnitt beginnen. Die Befehle
polyval
und polyfit
erleichtern den
Umgang mit Polynomen. Das Lösen von überbestimmten Gleichungssystemen kann
mit dem
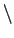 -Operator erfolgen. Das
Kapitel 10 beinhaltet eine detailierte Beschreibung der
Probleme.
-Operator erfolgen. Das
Kapitel 10 beinhaltet eine detailierte Beschreibung der
Probleme.
- Skriptnamen:
- fitlin.m, skegel.m, kegelfit.m
12.10.1 Fitten von Polynomen
- Die Datei
polydat.dat
enthält eine Messkurve. Die erste
Spalte enthält die
 -Werte, die zweite die
-Werte, die zweite die 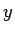 -Werte und die dritte den
Fehler
-Werte und die dritte den
Fehler 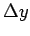 . Lesen Sie diese Daten ein.
. Lesen Sie diese Daten ein.
- Bestimmen Sie die besten Polynome nullter, erster, zweiter und
dritter Ordnung, die durch diese Daten passen.
- Zeichnen Sie die Datenpunkte mit Fehlerbalken (errorbar)
und die gefitteten Polynome (Beschriftung, Legende, ...).
12.10.2 Fitten von Polynomen mit teilweise vorgegebenen Koeffizienten
- Schreiben Sie ein Programm, das durch die Daten
polydat.dat
ein Polynom 3. Ordnung legt,
bei dem jedoch zwei
Koeffizienten bekannt sind:
- Koeffizient der 3. Ordnung (also der Koeffizient vor
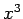 ):
):
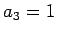 (Achtung der Koeffizient zur höchsten vorkommenden Potenz von
(Achtung der Koeffizient zur höchsten vorkommenden Potenz von
 steht in der MATLAB-Polynomdarstellung immer an erster Stelle im
Koeffizientenvektor)
steht in der MATLAB-Polynomdarstellung immer an erster Stelle im
Koeffizientenvektor)
- Koeffizient der 1. Ordnung (also der Koeffizient vor
 ):
):
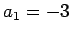
Dafür müssen Sie nun selbst ein lineares Gleichungssystem erstellen und
dieses mit Hilfe des
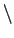 -Operators lösen. Dies liefert
Ihnen dann die gewünschten Koeffizienten. Überlegen Sie sich gut, wie die
rechte Seite dieses Gleichungssystems auszusehen hat.
-Operators lösen. Dies liefert
Ihnen dann die gewünschten Koeffizienten. Überlegen Sie sich gut, wie die
rechte Seite dieses Gleichungssystems auszusehen hat.
- Zeichnen Sie die Datenpunkte mit Fehlerbalken und das gefittete
Polynom (Beschriftung, Legende, ...).
12.10.3 Erzeugen von verrauschten Daten zu Testzwecken
- Erzeugen Sie für ein beliebiges Polynom verrauschte Testdaten. Wählen
Sie dazu einen Vektor mit
 -Werten und berechnen den entsprechenden
Vektor mit
-Werten und berechnen den entsprechenden
Vektor mit 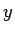 -Werten. Verrauschen Sie die Daten, indem Sie einen
normalverteilten Zufallsvektor mit der Varianz
-Werten. Verrauschen Sie die Daten, indem Sie einen
normalverteilten Zufallsvektor mit der Varianz 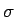 addieren
(sig*randn(size(x))).
addieren
(sig*randn(size(x))).
- Stellen Sie das Polynom und die verrauschten Daten mit Fehlerbalken
(
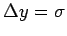 ) grafisch dar.
) grafisch dar.
- Fitten Sie ein Polynom entsprechender Ordnung (mit oder ohne
teilweise vorgegebene Koeffizienten) und stellen Sie es in derselben
Figur grafisch dar.
12.10.4 Fitten von Kegelschnitten
Wie schon in Übung 12.9.4 besprochen, kann
man Kegelschnitte durch verallgemeinerte quadratische Formen darstellen
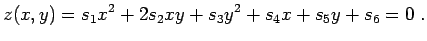 |
(12.36) |
Liegen nun 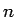 Datenpunkte für
Datenpunkte für  und
und 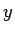 in den Spaltenvektren
in den Spaltenvektren 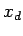 und
und
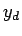 vor, kann man einen der Koeffizienten
vor, kann man einen der Koeffizienten 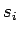 mit einem vorgegebenen Wert
belegen (z.B.:
mit einem vorgegebenen Wert
belegen (z.B.: 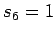 ) und den entsprechenden Term auf die rechte Seite des
Gleichungssystems bringen
) und den entsprechenden Term auf die rechte Seite des
Gleichungssystems bringen
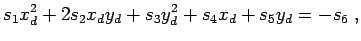 |
(12.37) |
wobei dieses Gleichungssystem nun nicht mehr homogen ist. Ist 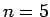 bekommt
man als Lösung des Gleichungssystems einen Kegelschnitt auf dem alle
Datenpunkte liegen. Ist
bekommt
man als Lösung des Gleichungssystems einen Kegelschnitt auf dem alle
Datenpunkte liegen. Ist 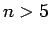 hat man es mit einem überbestimmten linearen
Gleichungssystem zu tun, das von MATLAB im ''Least Squares'' Verfahren
gelöst wird. Damit wird jener Kegelschnitt gefunden für den die Summe der
Abstandsquadrate
hat man es mit einem überbestimmten linearen
Gleichungssystem zu tun, das von MATLAB im ''Least Squares'' Verfahren
gelöst wird. Damit wird jener Kegelschnitt gefunden für den die Summe der
Abstandsquadrate
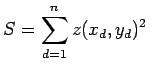 |
(12.38) |
ein Minimum ist.
Probleme mit der Lösung des Gleichungssystems bekommt man, wenn ein
''ungeeigneter'' Term auf die rechte Seite verschoben wird. Ungeeignet sind
Terme, deren Koeffizienten eigentlich Null ergeben würden, wie z.B. bei der
Parabel 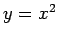 der oben gewählte Trem
der oben gewählte Trem 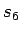 . Daher lohnt es sich, alle
. Daher lohnt es sich, alle 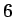 Terme nacheinander auf die rechte Seite zu bringen, das jeweilige
Gleichungssystem zu lösen und die Summe der Fehlerquadrate zu
berechnen. Damit kann man dann jene Lösung mit der geringsten Summe der
Fehlerquadrate als besten Fit verwenden.
Terme nacheinander auf die rechte Seite zu bringen, das jeweilige
Gleichungssystem zu lösen und die Summe der Fehlerquadrate zu
berechnen. Damit kann man dann jene Lösung mit der geringsten Summe der
Fehlerquadrate als besten Fit verwenden.
- Erzeugen Sie jetzt ein MATLAB-Skript skegel.m, das die Namen
aller zugehörigen Datenfiles einliest. Dazu gibt es die Möglichkeit diese
Namen in eine MATLAB-Struktur einzulesen:
files = dir('kschnitt*.dat'); % Struktur
anz = length(files); % Anzahl
k = 5; file = files(k).name; % Name des 5. Files
Der Benutzer soll dann eine Zahl und damit einen Filenamen auswählen, den
File einlesen und die Datenvektoren xd und yd belegen.
- Diese Daten werden der MATLAB-Funktion
[s,err2] = kegelfit(xd,yd)
übergeben, die dann den besten Fit für die Koeffizienten 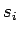 und die
zugehörige Summe der Fehlerquadrate err2 zurückgibt.
und die
zugehörige Summe der Fehlerquadrate err2 zurückgibt.
Folgen Sie bei der Erstellung der Funktion der oben beschriebenen Strategie
alle 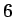 Terme abwechselnd auf die rechte Seite zu bringen. Für die
Aufteilung in Koeffizientenmatrix und Inhomogenitätsvektor eignet sich die
logische Indizierung hervorragend. Damit kann man das Problem leicht in
einer for-Schleife erledigen.
Terme abwechselnd auf die rechte Seite zu bringen. Für die
Aufteilung in Koeffizientenmatrix und Inhomogenitätsvektor eignet sich die
logische Indizierung hervorragend. Damit kann man das Problem leicht in
einer for-Schleife erledigen.
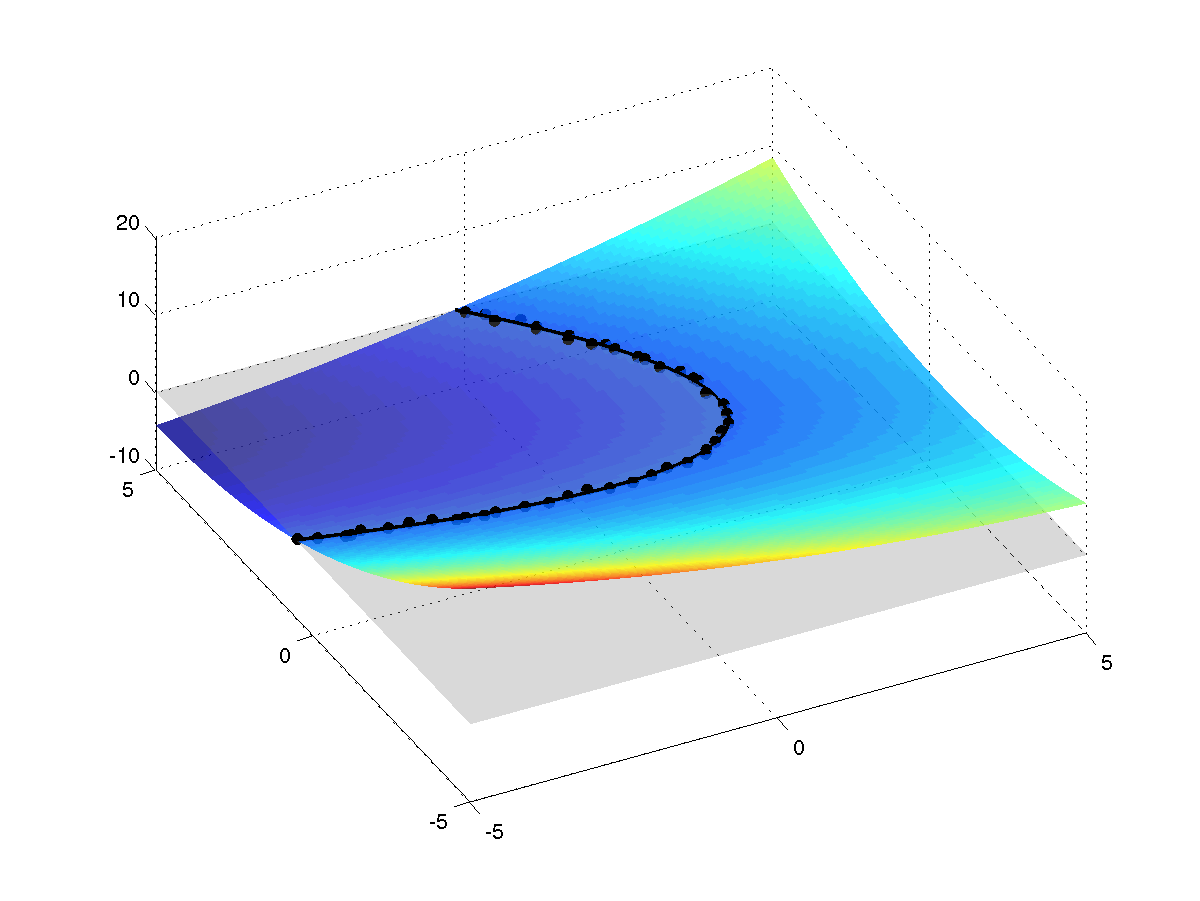
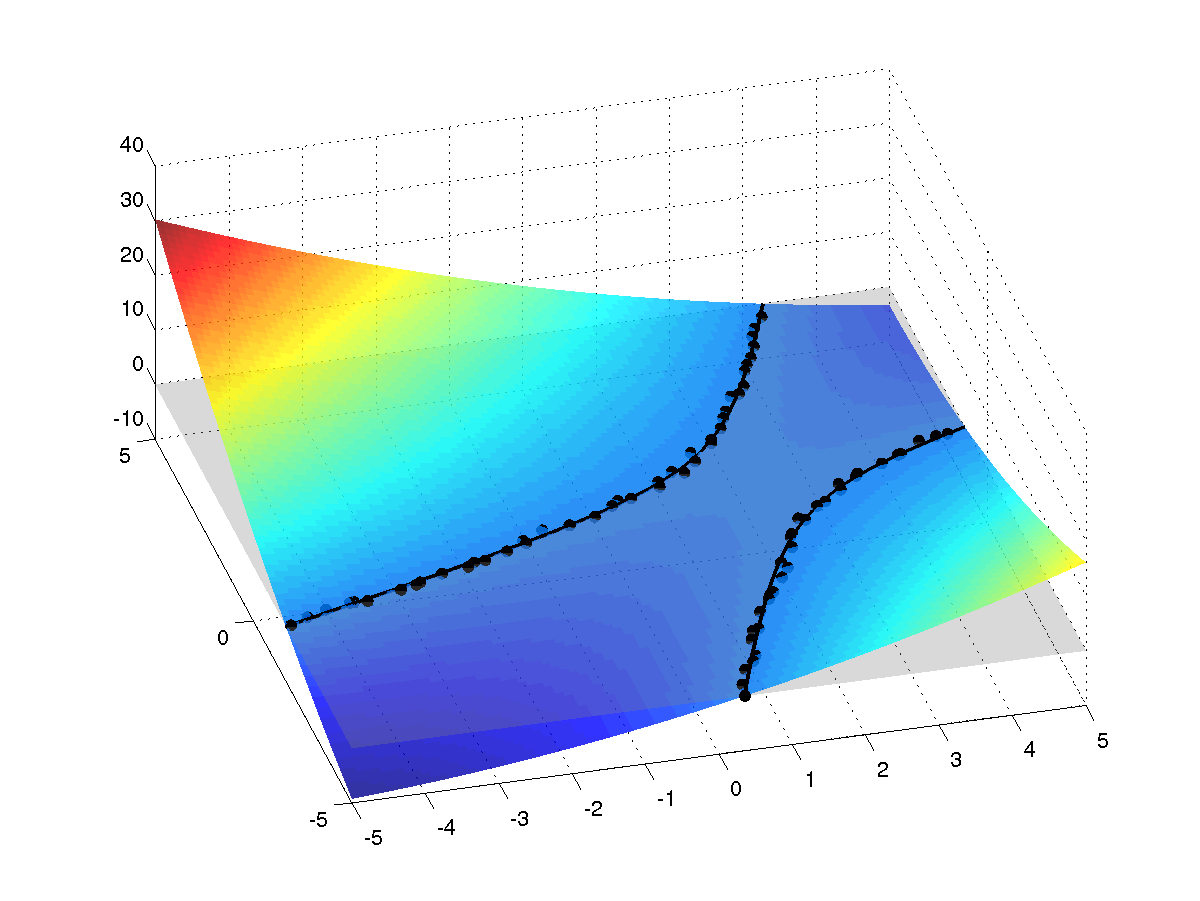
- Erstellen Sie danach im Skript eine Darstellung der Fläche
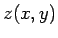 für
für
 - und
- und 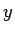 -Werte ungefähr im Bereich der Daten, zeichnen Sie ein
Konturlinie bei
-Werte ungefähr im Bereich der Daten, zeichnen Sie ein
Konturlinie bei 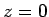 (entspricht Kegelschnitt) ein und plotten die
zugehörigen Datenpunkte. Diese sollten, wenn alles richtig ist, in der
nahen Umgebung des Kegelschnittes liegen.
(entspricht Kegelschnitt) ein und plotten die
zugehörigen Datenpunkte. Diese sollten, wenn alles richtig ist, in der
nahen Umgebung des Kegelschnittes liegen.
Winfried Kernbichler
2005-04-26
![]() -Operators lösen. Dies liefert
Ihnen dann die gewünschten Koeffizienten. Überlegen Sie sich gut, wie die
rechte Seite dieses Gleichungssystems auszusehen hat.
-Operators lösen. Dies liefert
Ihnen dann die gewünschten Koeffizienten. Überlegen Sie sich gut, wie die
rechte Seite dieses Gleichungssystems auszusehen hat.
![]() der oben gewählte Trem
der oben gewählte Trem ![]() . Daher lohnt es sich, alle
. Daher lohnt es sich, alle ![]() Terme nacheinander auf die rechte Seite zu bringen, das jeweilige
Gleichungssystem zu lösen und die Summe der Fehlerquadrate zu
berechnen. Damit kann man dann jene Lösung mit der geringsten Summe der
Fehlerquadrate als besten Fit verwenden.
Terme nacheinander auf die rechte Seite zu bringen, das jeweilige
Gleichungssystem zu lösen und die Summe der Fehlerquadrate zu
berechnen. Damit kann man dann jene Lösung mit der geringsten Summe der
Fehlerquadrate als besten Fit verwenden.
![]() Terme abwechselnd auf die rechte Seite zu bringen. Für die
Aufteilung in Koeffizientenmatrix und Inhomogenitätsvektor eignet sich die
logische Indizierung hervorragend. Damit kann man das Problem leicht in
einer for-Schleife erledigen.
Terme abwechselnd auf die rechte Seite zu bringen. Für die
Aufteilung in Koeffizientenmatrix und Inhomogenitätsvektor eignet sich die
logische Indizierung hervorragend. Damit kann man das Problem leicht in
einer for-Schleife erledigen.

