Next: 12.13 Funktionen Up: 12. ▄bungsbeispiele Previous: 12.11 Nichtlineares Fitten Contents
Eine ![]() -periodische Funktion
-periodische Funktion ![]() kann mit Hilfe einer Fourierreihe
approximiert werden. Diese Reihe konvergiert unter gewissen Bedingungen
gegen die Funktion
kann mit Hilfe einer Fourierreihe
approximiert werden. Diese Reihe konvergiert unter gewissen Bedingungen
gegen die Funktion ![]() und spielt in der Physik eine wichtige Rolle
(Wellenlehre, Wärmeleitung, Quantenmechanik, lineare
Differentialgleichungen).
und spielt in der Physik eine wichtige Rolle
(Wellenlehre, Wärmeleitung, Quantenmechanik, lineare
Differentialgleichungen).
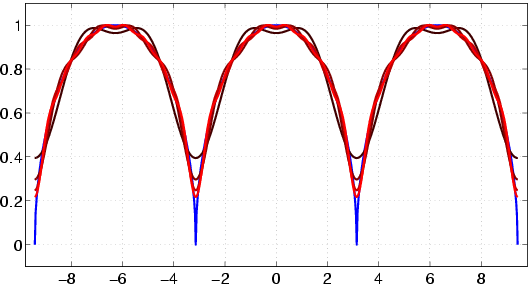
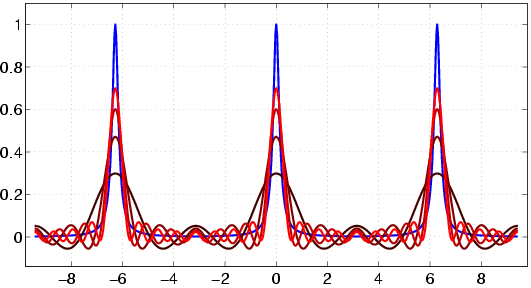
Die ![]() -te Teilsumme der Fourierreihe einer Funktion
-te Teilsumme der Fourierreihe einer Funktion ![]() lautet
lautet
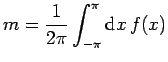
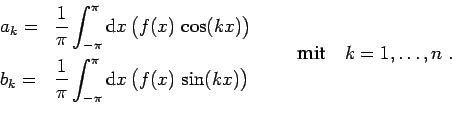
Die Integrale können mit quadl ausgeführt werden. Für die sin/cos-Integrale müssen inline-Funktionen funccos und funcsin definiert werden, die die Integranden bilden.
Tipp: Bei inline-Funktionen kann man mit den Befehlen formula und argnames die Funktion und ihre Argumente als String bzw. Zelle erhalten
f1 = inline('exp((x-x0).^2)','x','x0')
form = formula(f1) -> 'exp((x-x0).^2)'
args = argnames(f1) -> {'x','x0'}
und bekommt damit die benötigten Informationen. Bei der Definition der
inline-Funktionen verwendet man als erstes Argument eine
Zeichenkette, die jeweils die zu integrierende Funktion enthält. Für die
sin/cos-Integrale muss diese Zeichenkette sinnvoll aus form, args und sin/cos zusammengesetzt werden. Teilbereiche aus Zellen
bekommt man mit args{1} oder args{2:end}. Das Zusammensetzen
von Zeichenketten erfolgt wie bei Vektoren mit [], z.B. liefert ['sin','(x)'] den String 'sin(x)'. Bedenken Sie auch, dass der
Integrand neben
Probieren Sie am Anfang des Skripts fouriertest
[m,a,b]=fouriercoeff(f1,4) mit der inline-Funktion für f1=sin(x) aus. Funktioniert es und ist das Ergebnis sinnvoll? Warum
bekommt man für die Koeffizienten, die eigentlich 0 sein müssten, sehr
kleine Werte? Wie kann man das in fouriercoeff beheben?
Probieren Sie ihr Programm mit den inline-Funktionen für
![]() oder
oder
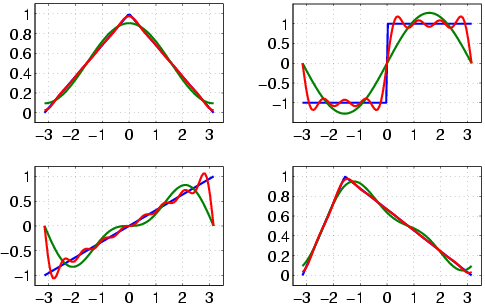
![]() aus. Wie schaut es jetzt mit den
Fourier-Koeffizienten aus?
aus. Wie schaut es jetzt mit den
Fourier-Koeffizienten aus?
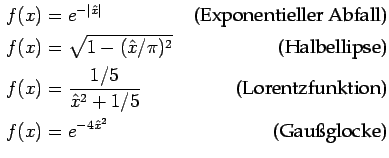
 |
|
In der Folge finden sich einige Übungsbeispiele, die momentan nicht verwendet werden.
Winfried Kernbichler 2005-04-26