12.13 Funktionen

Ziel:

In dieser Übungseinheit soll die Erstellung von Unterprogrammen und der Umgang mit diesen erlernt werden. Es werden drei Skriptfiles zur Verfügung gestellt:

scschleife.m, scpeaks3.m, sczykloide.m

Diese Skripts dienen zum Testen der zu erstellenden Funktionen und stellen die Ergebnisse außerdem graphisch dar. Abzugeben sind fünf MATLAB-Funktionen und ein kleines Skript:

schleife.m, peaks3.m, peaks3a.m, epizykloide.m, hypozykloide.m,
scinttest.m

Die einzelnen Funktionen sind relativ kurz und sollen das Wissen um Funktionen und Operatoren festigen.

Voraussetzung:

Die vorbereiteten Programme für die Übung können mit dem Befehl

!uebungsdaten

geladen werden. Die Übungsnummer ist 5.

Voraussetzung für die Übung sind vor allem die Kapitel 7 und 4 und die entsprechenden Diskussionen in der Vorlesung.

1. Die folgende Funktion und ihre Ableitung soll in Form einer MATLAB-Funktion schleife.m programmiert werden:

   $$y_{1,2} = \pm \frac{x}{a} \sqrt{a^4-x^2} \vert x\vert \leq a^2$$ (12.45)

   $$\frac{dy_{1,2}}{dx} = \pm \frac{a^4-2x^2}{a \sqrt{a^4-x^2}} \vert x\vert \leq a^2$$

   
   

   Der Aufruf für das Programm erfolgt mit

   [y1,dy1] = schleife(x,a),

   wobei außerhalb des Gültigkeitsbereichs von 12.45 NaN zurückgegeben werden soll. Die Variable x ist ein Vektor und a ist ein Skalar. Die Outputgrößen sollen Felder der gleichen Größe wie x sein. Die Werte für $y_2=-y_1$ und $dy_2/dx=-dy_1/dx$ brauchen nicht zurückgegeben zu werden.

   Die mögliche Fehlermeldung bei der Divison durch 0 an der Bereichsgrenze kann mit Hilfe der Befehle warning('off') und warning('on') vor und nach der betreffenden Zeile im Programm verhindert werden.

   talkprint
   Ergebnis von schleife für $a=2$.

2. Die folgende Funktion soll in Form einer MATLAB-Funktion peaks3.m programmiert werden:
   

   $$z(x,y,a) = 3 a_1 (1-\hat{x})^2 \exp \left( -\hat{x}^2 - (\hat{y}+1)^2 \right)$$

   $$- 10 a_2 \left( \hat{x}/5 - \hat{x}^3 - \hat{y}^5 \right) \exp \left( -\hat{x}^2 - \hat{y}^2 \right)$$ (12.46)

   $$- \frac{a_3}{3} \exp \left( -(\hat{x}+1)^2 - \hat{y}^2 \right) \; ,$$

   $$\hat{x}(x) = (x+\pi)\!\!\!\!\mod(2\pi) - \pi \; ,$$

   $$\hat{y}(y) = (y+\pi)\!\!\!\!\mod(2\pi) - \pi \; .$$

   
   Diese Funktion ist periodisch, das heißt

   $$z(x\!+\!2m\pi,y\!+\!2n\pi,a) = z(x,y,a) \qquad m,n \in \mathbb{Z} \; ,$$ (12.47)

   
   
   wobei das Periodizitätsintervall $[-\pi,\pi]$ ist.

   Der Aufruf für das Programm erfolgt mit

   [xx,yy,zz] = peaks3(x,y,a), bzw. mit
   [zz] = peaks3a(xx,yy,a).

   Die Variable a enthält die Parameter $a_i$ in Form eines Vektors. Die Variablen x und y sind auch Vektoren, wobei die Funktion für alle Kombinationen von x und y berechnet werden soll. Dazu wird zuerst der Befehl meshgrid verwendet, mit dem zwei gleich große Matrizen xx und yy erzeugt werden (siehe dazu auch 3.4.3 und insbesonders 3.1).

   Mit diesen Matrizen für xx und yy sollte nun die zweite Funktion gerufen werden. Bevor man nun die Formel für zz auswerten kann, muß man noch mit Hilfe des Befehls mod aus xx und yy die neuen Variablen xh und yh ( $\hat x,\hat y$) berechnen. Dadurch wird die Periodizität 12.47 sichergestellt. Diese Matrizen enthalten nun alle Werte um damit die Formel 12.46 auszuwerten. Überlegen Sie, welche Operatoren Sie verwenden müssen.

   Falls keine Werte für x und/oder y übergeben werden, sollten als Defaultwert 49 Punkte im Intervall $[-\pi,\pi]$ verwendet werden (linspace). Falls vom Dreiervektor a keine oder zuwenige Werte übergeben werden, sollten die fehlenden Werte auf $1$ gesetzt werden.

   talkprint
   Ergebnis von peaks3 für $a=[1,1,1]$ im Intervall $[-\pi,\pi]$ und mit periodischer Fortsetzung.

3. Zykloiden (Rollkurven) sind Kurven, die dadurch entstehen, dass ein Kreis K auf einer Leitkurve L abrollt ohne zu gleiten. Bezeichnet M einen Punkt auf der Peripherie des Kreises K, so beschreibt M bei dieser Bewegung eine Zykloide. Ist C der Mittelpunkt von K und M$^\prime$ ein Punkt auf der Verbindungsstrecke CM, so beschreibt M$^\prime$ eine verkürzte Zykloide. Liegt M $^{\prime\prime}$ außerhalb des Kreises auf der Verlängerung von CM, so beschreibt M $^{\prime\prime}$ eine verlängerte Zykloide.

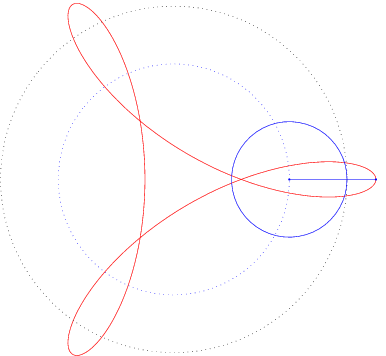
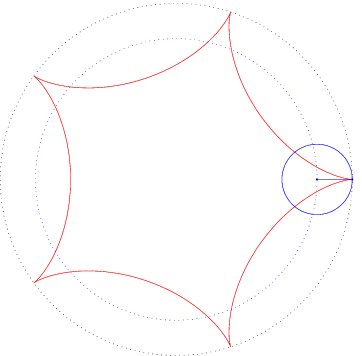
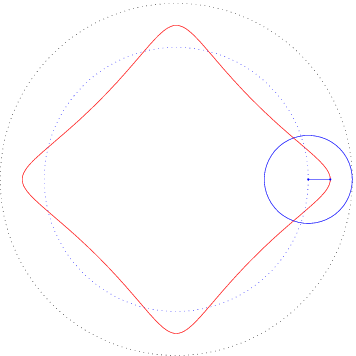
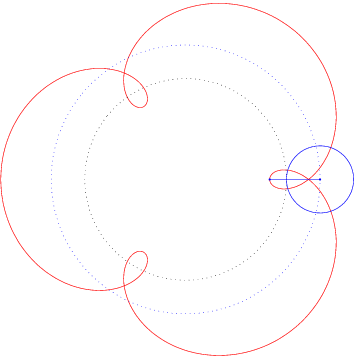
   Ist die Leitkurve L ebenfalls ein Kreis, so spricht man von Epizykloiden, wenn der Kreis K auf der Außenseite abrollt, und von Hypozykloiden, wenn der Kreis K auf der Innenseite abrollt.

   Ist $a$ der Radius des rollenden Kreises K, $b$ der Radius der Leitkurve L und $\lambda$ der Verlängerungs- bzw. Verkürzungsfaktor, so gilt für die Parameterdarstellung der Epizykloide,
   

   $$x = (a+b)\cos\phi - \lambda a \cos\left( \frac{(a+b)\phi}{a}\right)$$

   $$y = (a+b)\sin\phi - \lambda a \sin\left( \frac{(a+b)\phi}{a}\right) \; ,$$ (12.48)

   
   mit

   $$a=\frac{qb}{p}>0, \qquad b>0, \qquad p,q \in \mathbb{N}, \qquad 0 \leq \phi \leq 2q\pi \; .$$ (12.49)

   
   

   Für die Hypozykloide gilt,
   

   $$x = (b-a)\cos\phi - \lambda a \cos\left( \frac{(b-a)\phi}{a}\right)$$

   $$y = (b-a)\sin\phi - \lambda a \sin\left( \frac{(b-a)\phi}{a}\right) \; ,$$ (12.50)

   
   mit

   $$a=\frac{qb}{p}, \qquad b>a>0, \qquad p,q \in \mathbb{N}, \qquad 0 \leq \phi \leq 2q\pi \; .$$ (12.51)

   
   

   Zu programmieren sind nun zwei Funktionen

   [x,y] = epizykloide (b,p,q,l,n) und
   [x,y] = hypozykloide(b,p,q,l,n),

   wobei hier l für $\lambda$ steht. Mit n wird die Länge der Vektoren x und y angegeben.

   Die Minimalversion der Funktionen muß nun $\phi$ (linspace), $a$, und damit dann $x$ und $y$ berechnen.

   Weiters sollte man noch die Anzahl der Inputvariablen überprüfen und Defaultwerte setzen, $b=1$, $p=3$, $q=1$, $\lambda=1$ und $n=500$. Zusätzlich sollte man die Zulässigkeit der Werte für die Inputvariablen überprüfen (nargin) und gegebenfalls Fehlermitteilungen (error) schreiben. Man kann auch durch Anwendung des Befehls floor sicherstellen, dass $p$ und $q$ als ganzzahlige Werte verwendet werden. Damit stellt man sicher, dass sich die Kurve jeweils am Ende schließt.

   Einige typische Beispiele können Sie hier sehen:

   talkprint
   talkprint
   talkprint

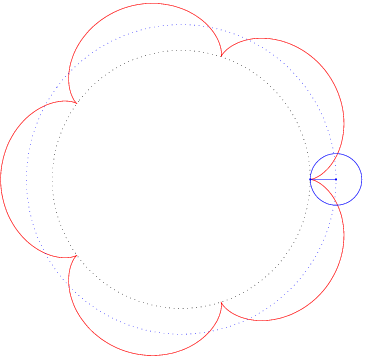
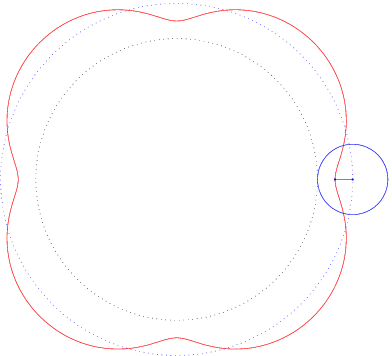
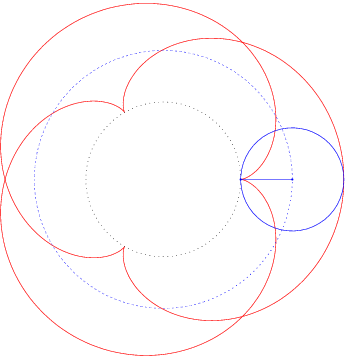
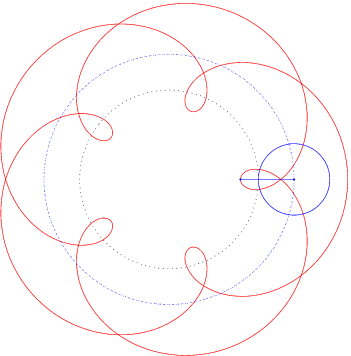
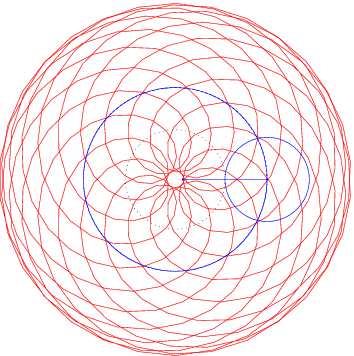
4. Schreiben Sie ein kleines Skript scinttest.m das die Integrale

   $$A_1(a) = \int_{0}^{a} dx \; y_1(x,a)$$ (12.52)

   
   
   mit $y_1(x,a)$ aus 12.45 und

   $$A_2(a) = \int_{-\pi}^{\pi}\int_{-\pi}^{\pi} dxdy \; z(x,y,a)$$ (12.53)

   
   
   mit $z(x,y,a)$ aus 12.46 berechnet.

   Verwenden Sie dazu die MATLAB-Funktionen quadl und dblquad. Bedienen Sie sich der MATLAB-Hilfe bzw. des Kapitels 7.1.8 um herauszufinden, wie diese Integrationsroutinen funktionieren. Überlegen Sie auch, ob Sie im zweiten Fall peaks3 oder peaks3a verwenden müssen.

   Geben Sie die berechneten Größen von Fläche und Volumen mit disp formatiert aus.