12.14 Gaußfunktion
- Ziel:
- Bei der vorliegenden Übung wird nochmals die Erstellung von
Funktionen geübt. Darüber hinaus wird hier auch Wert auf die graphische
Darstellung in zwei und drei Dimensionen gelegt.
Abzugeben sind die Unterprogramme
gauss.m, gauss1d.m, gauss2d.m und gausstest.m.
- Voraussetzung:
- Voraussetzung für
die Übung ist das Kapitel über
Programmeinheiten 7 und über
Graphik 11. Als kleine Einführung zum Plotten können die
Files htplot2d.m
und htplot2da.m
der verwendet werden.
In der Wahrscheinlichkeitsrechnung und auch in der Physik hat die
Normalverteilung bzw. Gaußverteilung eine große Bedeutung. Sie ist definiert
durch
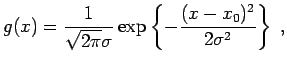 |
(12.54) |
wobei 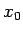 und
und 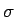 die Parameter der Verteilung sind. In
die Parameter der Verteilung sind. In 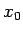 liegt sowohl das Maximum als auch das Symmetriezentrum, und
liegt sowohl das Maximum als auch das Symmetriezentrum, und 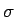 ist
der Abstand von diesem Zentrum zu den Wendepunkten. Wie für jede
Wahrscheinlichkeitsverteilung gilt
ist
der Abstand von diesem Zentrum zu den Wendepunkten. Wie für jede
Wahrscheinlichkeitsverteilung gilt
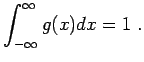 |
(12.55) |
In der Physik verwendet man häufig auch eine Summation über mehrere
Gaußfunktionen mit jeweils unterschiedlichen Parametern. Dies hat den Sinn,
dass man gleichzeitig mehrere Maxima darstellen kann. Allgemein kann man die
Funktion dann definieren als
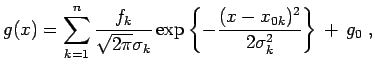 |
(12.56) |
wobei 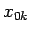 und
und 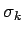 die gleiche Bedeutung wie vorher haben. Der
Parameter
die gleiche Bedeutung wie vorher haben. Der
Parameter 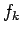 ist ein Multiplikator, um Peaks unterschiedlicher Höhe
darstellen zu können. Die Summation erfolgt über alle
ist ein Multiplikator, um Peaks unterschiedlicher Höhe
darstellen zu können. Die Summation erfolgt über alle 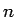 Werte der Parameter
Werte der Parameter
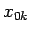 ,
, 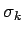 und
und 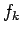 . Zusätzlich kann die ganze Funktion noch um
den Wert
. Zusätzlich kann die ganze Funktion noch um
den Wert 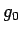 vertikal verschoben sein. Für
vertikal verschoben sein. Für 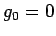 gilt natürlich
gilt natürlich
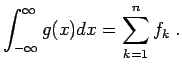 |
(12.57) |
In zwei Dimensionen kann die Gaußverteilung folgendermaßen definiert werden
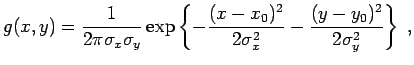 |
(12.58) |
wobei nun 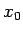 ,
, 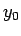 ,
, 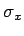 und
und 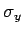 die Parameter der
Verteilung sind. Auch hier gilt die Normierungsbedingung
die Parameter der
Verteilung sind. Auch hier gilt die Normierungsbedingung
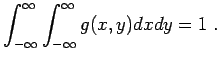 |
(12.59) |
Die Summation über mehrere Peaks kann natürlich auch hier erfolgen,
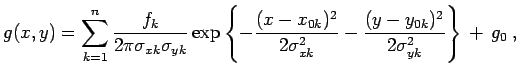 |
(12.60) |
wobei die Parameter die analoge Bedeutung wie in 12.56
haben. Für 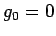 gilt natürlich
gilt natürlich
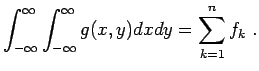 |
(12.61) |
Schreiben Sie nun eine Funktion gauss1d.m, welche die Formel
12.56 für beliebige numerische Arrays von  auswertet.
Die Ausgabegröße sollte ein Feld
auswertet.
Die Ausgabegröße sollte ein Feld 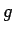 sein, das die gleiche Größe und
Dimension wie
sein, das die gleiche Größe und
Dimension wie  hat. Die Parameter
hat. Die Parameter 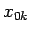 ,
, 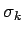 und
und 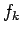 können
ebenfalls in numerischen Arrays gespeichert sein, welche die gleiche Größe
haben müssen. Der Parameter
können
ebenfalls in numerischen Arrays gespeichert sein, welche die gleiche Größe
haben müssen. Der Parameter 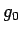 muss natürlich ein Skalar sein.
muss natürlich ein Skalar sein.
- Die Deklaration der Funktion sollte so aussehen.
function [g] = gauss1d(x,x0,s,f,g0)
x0 enthält alle 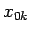 -Werte, s alle
-Werte, s alle
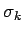 -Werte, und
f alle
-Werte, und
f alle 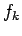 -Werte.
-Werte.
- Setzen Sie die Defaultwerte
![$ x_{0}=[-1,1]$](img497.gif) ,
,
![$ \sigma=[0.5,1]$](img498.gif) ,
,
![$ f=[1,0.5]$](img788.gif) und
und 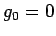 (nargin).
(nargin).
- Überprüfen Sie die Eingabegrößen.
- Initialisieren Sie
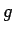 als Feld mit lauter Nullen in der Größe von
als Feld mit lauter Nullen in der Größe von
 .
.
- Bilden Sie die Summe über alle Werte (
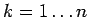 ) der Parameter mit
Hilfe einer einzigen for-Schleife. Vergessen Sie dabei nicht,
dass
) der Parameter mit
Hilfe einer einzigen for-Schleife. Vergessen Sie dabei nicht,
dass  ein Array sein kann.
ein Array sein kann.
- Probieren Sie die Funktion mit Hilfe des Skripts gausstest.m
aus und machen Sie einen Plot
plot(x,g)
Wählen Sie den  -Vektor in einem vernünftigen Bereich, damit die
Funktion
-Vektor in einem vernünftigen Bereich, damit die
Funktion 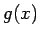 sinnvoll dargestellt wird
(linspace). Beschriften Sie den Plot mit Achsenbeschriftung und
Titel.
sinnvoll dargestellt wird
(linspace). Beschriften Sie den Plot mit Achsenbeschriftung und
Titel.
Schreiben Sie nun eine Funktion gauss2d.m, welche die Formel
12.60 auswertet. Die Inputgrößen  and
and 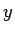 können
entweder gleich große Arrays sein oder eine der beiden ist ein Array und
die andere ein Skalar.
Im ersten Fall (gleich groß) wird die Funktion für alle Punkte
können
entweder gleich große Arrays sein oder eine der beiden ist ein Array und
die andere ein Skalar.
Im ersten Fall (gleich groß) wird die Funktion für alle Punkte 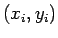 berechnet, im zweiten Fall (ein Skalar) für alle Punkte
berechnet, im zweiten Fall (ein Skalar) für alle Punkte 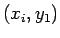 oder
oder
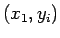 .
Die Ausgabegröße sollte ein Feld
.
Die Ausgabegröße sollte ein Feld 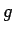 sein, das die
gleiche Größe und Dimension wie das Array
sein, das die
gleiche Größe und Dimension wie das Array  oder
oder 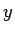 hat. (Aufpassen, da
hat. (Aufpassen, da
 oder
oder 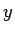 auch ein Skalar sein können!) Die Parameter
auch ein Skalar sein können!) Die Parameter 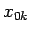 ,
,
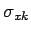 ,
, 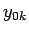 ,
,
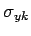 und
und 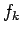 können ebenfalls in
numerischen Arrays gespeichert sein, welche die gleiche Größe haben müssen.
Der Parameter
können ebenfalls in
numerischen Arrays gespeichert sein, welche die gleiche Größe haben müssen.
Der Parameter 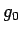 muss natürlich wieder ein Skalar sein.
muss natürlich wieder ein Skalar sein.
- Die Deklaration der Funktion sollte so aussehen.
function [g] = gauss2d(x,y,x0,sx,y0,sy,f,g0)
- Setzen Sie die Defaultwerte für zwei Peaks Ihrer Wahl.
- Überprüfen Sie die Eingabegrößen.
- Initialisieren Sie
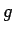 als Feld mit lauter Nullen in der Größe von
als Feld mit lauter Nullen in der Größe von
 oder
oder 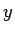 .
.
- Bilden Sie nun die Summe in 12.60 mit einer
for-Schleife über alle Werte
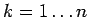 .
.
- Probieren Sie die Funktion mit Hilfe des Skripts gausstest.m
aus und machen Sie eine dreidimensionale Darstellung
surf(xx,yy,g) oder
mesh(xx,yy,g).
Wählen Sie den  -Vektor und den
-Vektor und den 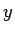 -Vektor in einem vernünftigen
Bereich und bilden Sie mit meshgrid
Arrays für die Darstellung
der Funktion.
-Vektor in einem vernünftigen
Bereich und bilden Sie mit meshgrid
Arrays für die Darstellung
der Funktion.
- Beschriften Sie den Plot und probieren Sie sinnvolle Darstellungen in
Subplots einer Figure. Zum Beispiel sollte man auch Konturplots
ausprobieren.
- Eine numerische Integration kann in MATLAB mit Hilfe der Funktion
quadl
durchgeführt werden. Ein Aufruf zum Auswerten des 1-D
Integrals kann so aussehen,
flaeche = quadl('gauss',x1,x2,tol,trace,parameter),
wobei hier gauss die Funktion ist, über die von x1 bis x2
integriert wird. Für die Genauigkeit tol und für den Wert trace
können zum Testen leere Felder [] eingegeben werden. Danach folgen
die Parameter der Gaußfunktion x0, s, f und y0.
- Schreiben Sie am Ende von gausstest.m den Code für die
Integration und geben Sie das Ergebnis formatiert aus. Überprüfen Sie es
mit der analytischen Lösung 12.57. Was passiert, wenn
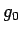 von Null verschieden ist?
von Null verschieden ist?
- Probieren Sie es mit verschiedenen Parametern aus und überprüfen Sie
12.57. Bedenken Sie dabei, dass die
Integrationsgrenzen weit genug entfernt von den Maxima sind, damit
12.57 näherungsweise erfüllt sein kann. Natürlich
dürfen sie aber nicht
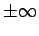 sein.
sein.
- Machen Sie das Gleiche für die 2-dimensionale Gaußfunktion.
- Schreiben Sie die Funktion gauss.m, die auf zwei Arten
aufgerufen
werden kann,
[g] = gauss(a,x) oder
[g] = gauss(a,x,y).
- Aus ihr werden je nach Anzahl der Inputparameter (2 oder 3) die 1-D
oder 2-D Funktionen gauss1d oder gauss2d aufgerufen. Der
Vektor a soll dabei alle Parameter enthalten, also
![$ [x_{0k},\sigma_{k},f_{k},g_{0}]$](img795.gif) in 2-D, oder
in 2-D, oder
![$ [x_{0k},\sigma_{xk},y_{0k},\sigma_{yk},f_{k},g_{0}]$](img796.gif) in
3-D.
in
3-D.
- Diese Vektoren haben die Länge
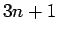 bzw.
bzw. 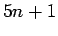 , wobei
, wobei 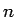 die
Anzahl der Peaks ist. Vor dem Aufruf von gauss1d oder gauss2d
müssen Sie auf die dort benötigten Inputparameter aufgespalten
werden. Bestimmen Sie daher zuerst die Länge von a, daraus dann
n, und damit sollte die Aufspaltung klar sein. Sollte die Länge von
a nicht stimmen, soll eine error-Meldung ausgegeben werden.
die
Anzahl der Peaks ist. Vor dem Aufruf von gauss1d oder gauss2d
müssen Sie auf die dort benötigten Inputparameter aufgespalten
werden. Bestimmen Sie daher zuerst die Länge von a, daraus dann
n, und damit sollte die Aufspaltung klar sein. Sollte die Länge von
a nicht stimmen, soll eine error-Meldung ausgegeben werden.
- Testen Sie die neue Routine im Skript gausstest.m mit zwei
möglichst sinnvollen Aufrufen.
Geben Sie gauss.m, gauss1d.m, gauss2d.m und das Skript
gausstest.m ab. Verwenden Sie dabei wieder !uebungsabgabe.
Winfried Kernbichler
2005-04-26
![]() auswertet.
Die Ausgabegröße sollte ein Feld
auswertet.
Die Ausgabegröße sollte ein Feld ![]() sein, das die gleiche Größe und
Dimension wie
sein, das die gleiche Größe und
Dimension wie ![]() hat. Die Parameter
hat. Die Parameter ![]() ,
, ![]() und
und ![]() können
ebenfalls in numerischen Arrays gespeichert sein, welche die gleiche Größe
haben müssen. Der Parameter
können
ebenfalls in numerischen Arrays gespeichert sein, welche die gleiche Größe
haben müssen. Der Parameter ![]() muss natürlich ein Skalar sein.
muss natürlich ein Skalar sein.
![]() and
and ![]() können
entweder gleich große Arrays sein oder eine der beiden ist ein Array und
die andere ein Skalar.
Im ersten Fall (gleich groß) wird die Funktion für alle Punkte
können
entweder gleich große Arrays sein oder eine der beiden ist ein Array und
die andere ein Skalar.
Im ersten Fall (gleich groß) wird die Funktion für alle Punkte ![]() berechnet, im zweiten Fall (ein Skalar) für alle Punkte
berechnet, im zweiten Fall (ein Skalar) für alle Punkte ![]() oder
oder
![]() .
Die Ausgabegröße sollte ein Feld
.
Die Ausgabegröße sollte ein Feld ![]() sein, das die
gleiche Größe und Dimension wie das Array
sein, das die
gleiche Größe und Dimension wie das Array ![]() oder
oder ![]() hat. (Aufpassen, da
hat. (Aufpassen, da
![]() oder
oder ![]() auch ein Skalar sein können!) Die Parameter
auch ein Skalar sein können!) Die Parameter ![]() ,
,
![]() ,
, ![]() ,
,
![]() und
und ![]() können ebenfalls in
numerischen Arrays gespeichert sein, welche die gleiche Größe haben müssen.
Der Parameter
können ebenfalls in
numerischen Arrays gespeichert sein, welche die gleiche Größe haben müssen.
Der Parameter ![]() muss natürlich wieder ein Skalar sein.
muss natürlich wieder ein Skalar sein.