Subsections
1.6 Programmpakete
Der Schwerpunkt unserer Arbeit wird auf dem Programmpaket MATLAB basieren. Der Name steht für MATrix LABoratory und bezieht sich auf eine
herausragende Eigenschaft von MATLAB, nämlich die Fähigkeit fast alle Befehle
auf Vektoren bzw. Matrizen anwenden zu können.
talkprint
Das Paket ist gleichzeitig:
- eine Art Taschenrechner auch für Vektoren und Matrizen
- eine Programmiersprache
- ein Compiler
- ein mächtiges Programm zur Visualisierung
- ein Tool zur Erstellung von Graphical User Interfaces (GUI)
- erweiterbar durch Toolboxen zu den verschiedensten Themenbereichen
- ein graphisches Werkzeug zur Simulation von komplexen Abläufen
(SIMULINK)
- eine Schnittstelle zu symbolischen Rechenprogrammen (MAPLE)
- eine Schnittstelle zu anderen Programmiersprachen (C, FORTRAN)
In Ergänzung dazu wird auf Seite der symbolischen Programmpakete
MAPLE vorgestellt werden. Dabei werden wir uns maximal mit wenigen Grundzügen
bschäftigen bzw. die Verbindung zwischen MATLAB und MAPLE kennenlernen.
talkprint
Numerischen Programme wie MATLAB und symbolische Programme wie MAPLE oder
MATHEMATICA unterscheiden sich in folgendem Punkt:
- MATLAB
- Numerische Programme arbeiten mit Zahlenwerten, das heißt, einer Variablen
muss ein Wert zugewiesen werden,
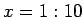 (Vektor der Zahlen 1 bis 10), und
dann können Operationen darauf
angewandt werden, z.B.:
(Vektor der Zahlen 1 bis 10), und
dann können Operationen darauf
angewandt werden, z.B.: 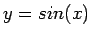 .
Resultate liegen daher immer ``numerisch''
vor und sind mit der inhärenten Ungenauigkeit von numerischen Darstellungen
behaftet. Numerische Programme haben daher ihre Bedeutung bei einer großen
Anzahl ``symbolisch'' nicht lösbarer Probleme bzw. bei der Verarbeitung von
numerisch vorliegenden Daten (Messdaten, ...).
.
Resultate liegen daher immer ``numerisch''
vor und sind mit der inhärenten Ungenauigkeit von numerischen Darstellungen
behaftet. Numerische Programme haben daher ihre Bedeutung bei einer großen
Anzahl ``symbolisch'' nicht lösbarer Probleme bzw. bei der Verarbeitung von
numerisch vorliegenden Daten (Messdaten, ...).
- MAPLE
- Symbolische Programme hingegen arbeiten mit Variablen, denen keine
numerischen Werte zugewiesen sind. Hier liefert z.B. die Eingabe
y=int(x^2,x) das Ergebnis
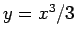 . Danach können dann bei Bedarf
Werte für
. Danach können dann bei Bedarf
Werte für  eingesetzt werden. Lösbare Probleme können daher auf exakte
Art und Weise gelöst werden.
eingesetzt werden. Lösbare Probleme können daher auf exakte
Art und Weise gelöst werden.
Der Unterschied sei hier am Beispiel der Differentiation erklärt. In einem
symbolischen Rechenprogramm kann die Differentiation exakt ausgeführt werden,
falls eine Lösung existiert
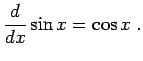 |
(1.1) |
In der Numerik hingegen liegen Zahlenwerte, z.B. in Form eines Vektors vor
![$\displaystyle = \left[ x_1, x_2, \dots, x_n \right] \; ,$](img7.gif) |
(1.2) |
wobei 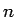 die Anzahl der Elemente im Vektor
die Anzahl der Elemente im Vektor 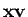 ist.
Mit dem Befehl
ist.
Mit dem Befehl
![$\displaystyle {\bf yv} = \sin({\bf xv}) \; , {\bf yv} = \left[ y_1, y_2, \dots, y_n \right] \; ,$](img10.gif) |
(1.3) |
kann man nun einen Vektor 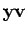 der gleichen Länge
der gleichen Länge 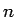 erzeugen.
Die Differentiation kann jetzt aber nur näherungsweise mit Hilfe des
Differenzenquotienten
erzeugen.
Die Differentiation kann jetzt aber nur näherungsweise mit Hilfe des
Differenzenquotienten
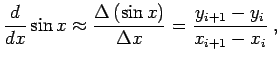 |
(1.4) |
erfolgen.
Diese Vorgangsweise mag hier unlogisch erscheinen, sie funktioniert aber auch
dann, wenn überhaupt kein funktionaler Zusammenhang bekannt ist (z.B.:
Messdaten) oder wenn ein Problem nicht exakt lösbar ist. In der Realität ist
deshalb eine numerische Behandlung von Problemen häufig notwendig. Man muss
sich aber natürlich immer im Klaren sein, dass die Numerik mit
Ungenauigkeiten behaftet ist.
1.6.1 Software Version
Im Computerraum Physik ist derzeit die neueste Version MATLAB 6.5
installiert:
MATLAB Version 7.0.0.19901 (R14)
Winfried Kernbichler
2005-04-26