Nächste Seite: Least-Squares Approximation Aufwärts: Numerische Methoden in der Vorherige Seite: Numerische Methoden zur Lösung
Es seien die ![]() - und die
- und die ![]() -Koordinaten von
-Koordinaten von ![]() Punkten gegeben. Die
Zuordnung der Koordinaten sei eindeutig d.h. zu jedem
Punkten gegeben. Die
Zuordnung der Koordinaten sei eindeutig d.h. zu jedem ![]() -Wert
gehöre ein und nur ein
-Wert
gehöre ein und nur ein ![]() -Wert. Weiters soll angenommen werden, daß
die
-Wert. Weiters soll angenommen werden, daß
die ![]() -Werte nach ihrer Größe geordnet vorliegen; sie müssen aber
keineswegs äquidistant sein.
-Werte nach ihrer Größe geordnet vorliegen; sie müssen aber
keineswegs äquidistant sein.
Eine wichtige Forderung an die Punktmenge ist mathematisch schwer zu
definieren. Sie lautet: Die Stützpunkte
![]() ,
,
![]() sollen einen funktionellen Zusammenhang zwischen
sollen einen funktionellen Zusammenhang zwischen
![]() und
und ![]() phänomenologisch befriedigend repräsentieren.
Die Abb.3.1 zeigt, wie das gemeint ist.
phänomenologisch befriedigend repräsentieren.
Die Abb.3.1 zeigt, wie das gemeint ist.
Geht man nun davon aus, daß die gegebene Punktmenge im Intervall
![]() repräsentativ ist, so kann eine Interpolationsfunktion
repräsentativ ist, so kann eine Interpolationsfunktion
![]() wie folgt definiert werden:
wie folgt definiert werden:
Das folgende aus [13], S.127: Der Konstruktionsweg für die
Interpolationsfunktion besteht darin, eine endliche Menge Funktionen
![]() zugrunde zu legen, die über dem Intervall
zugrunde zu legen, die über dem Intervall ![]() linear unabhängig sind, und die Interpolationsfunktion als
Linearkombination dieser Funktionen anzusetzen, also
linear unabhängig sind, und die Interpolationsfunktion als
Linearkombination dieser Funktionen anzusetzen, also
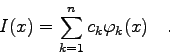
Typische Entwicklungsfunktionen für ![]() sind
sind
Sehr häufig angewendet wird die polynomiale Interpolation,
d.h. als Ansatz dient ein Polynom ![]() -ten Grades mit den (vorerst)
allgemeinen Koeffizienten
-ten Grades mit den (vorerst)
allgemeinen Koeffizienten ![]() :
:
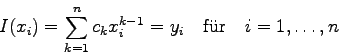
Lagrange hat eine Formel angegeben, die es erlaubt, ein
derartiges Interpolationspolynom in geschlossener Form anzuschreiben:
Die numerische Berechnung von Werten des Interpolationspolynoms kann direkt aus der Gleichung (3.4) erfolgen. In der einschlägigen Literatur findet man jedoch zahlreiche Algorithmen für die Auswertung von (3.4), die für den Computer besser geeignet sind, wie z.B. den Neville'schen Algorithmus ([9], S.80ff) oder den Formalismus von Newton ([2], S.135ff, Programme S.345ff). In diesem Skriptum wird auf keines dieser Bibliotheksprogramme näher eingegangen, weil sie in der Praxis von nur beschränkter Bedeutung sind. Die Begründung dafür folgt im folgenden Beispiel (aus [14], S.2ff):
Gegeben seien 11 Punkte der Funktion
![\includegraphics[scale=0.9]{num3_fig/aint2}](img8.png) |
Damit ist das Problem evident: das Polynom beschreibt die zu interpolierende
Funktion nur im Bereich ![]() gut. An den Rändern des
Interpolationsintervalles kommt es hingegen zu massiven Verfahrensfehlern.
Die Ursache dafür ist die Neigung von Interpolationspolynomen, zwischen den
Stützpunkten zu oszillieren. Da diese Oszillationen mit steigendem Grad des
Polynoms i.a. zunehmen, sind die gemäß (3.4) bestimmten
Interpolationskurven in vielen Fällen in eindeutigem Widerspruch zur
'Glätte-Bedingung' (3.2) und somit unbrauchbar!
gut. An den Rändern des
Interpolationsintervalles kommt es hingegen zu massiven Verfahrensfehlern.
Die Ursache dafür ist die Neigung von Interpolationspolynomen, zwischen den
Stützpunkten zu oszillieren. Da diese Oszillationen mit steigendem Grad des
Polynoms i.a. zunehmen, sind die gemäß (3.4) bestimmten
Interpolationskurven in vielen Fällen in eindeutigem Widerspruch zur
'Glätte-Bedingung' (3.2) und somit unbrauchbar!
Im folgenden wird nun gezeigt, daß es meist zielführender ist, eine gegebene Punktmenge stückweise unter Verwendung von Polynomen niedriger Grade zu interpolieren.
Ausgangspunkt für die Spline-Interpolation sind Polynome vom Grad 3:
![\begin{displaymath}
I(x) = \quad\left\{
\begin{array}{c}
P^{1}(x) \quad \mbox{f...
...mbox{f\uml ur} \quad x\in [x_{n-1},x_{n}]
\end{array}
\right.
\end{displaymath}](img376.gif)
Die insgesamt ![]() Polynomkoeffizienten
Polynomkoeffizienten ![]() ,
, ![]() ,
, ![]() und
und
![]() werden nun so ermittelt,daß
werden nun so ermittelt,daß
Im Prinzip können zur Spline-Interpolation auch Polynome höherer Grade herangezogen werden. Da aber die kubischen Splines am weitaus häufigsten verwendet werden, soll hier nur von diesen die Rede sein (Informationen, Formeln und Programme zu Splines 5. Grades s. z.B. [2],S. 154ff bzw. S.358ff).
Für die kubischen Splines ergeben sich also die folgenden
Bedingungen:
Die folgenden Ausführungen sind nun wieder für natürliche
kubische Splines:
Im Prinzip könnte man aus dem Gleichungssystem (3.7) und (3.8)
alle Spline-Koeffizienten berechnen. In der Praxis geht man etwas anders vor,
nämlich über die folgenden Gleichungen, die eindeutig aus (3.7) und
(3.8) resultieren. Die entsprechende Ableitung ist nicht schwierig,
aber sehr langwierig, und soll daher hier wegbleiben:
(3.10) bedeutet ein lineares inhomogenes Gleichungssystem ![]() -ter
Ordnung für die Unbekannten
-ter
Ordnung für die Unbekannten
![]() , wobei die
Koeffizientenmatrix tridiagonal und symmetrisch ist.
, wobei die
Koeffizientenmatrix tridiagonal und symmetrisch ist.
Aus der Kenntnis der ![]() und
und ![]() ergeben sich für die übrigen
Spline-Koeffizienten die Bestimmungsgleichungen
ergeben sich für die übrigen
Spline-Koeffizienten die Bestimmungsgleichungen
Das Programm SPLINE berechnet die Koeffizienten
![]() natürlicher kubischer Splines für eine gegebene Menge von Stützpunkten
natürlicher kubischer Splines für eine gegebene Menge von Stützpunkten
![]() ,
, ![]() ,
wobei die
,
wobei die ![]() monoton ansteigend geordnet sein müssen.
monoton ansteigend geordnet sein müssen.
INPUT-Parameter:
OUTPUT-Parameter:
Interne Felder:
Programmstruktur:
=15cm
Struktogramm 9SPLINE(N,X,Y,A,B,C,D)I=1(1)N-1X(I) ![]() X(I+1)H(I):=X(I+1)-X(I)
X(I+1)H(I):=X(I+1)-X(I)
R(I):=Y(I+1)-Y(I)(return 'Reihenfolge der x inkorrekt')J=1(1)N-2HD(J):=2.0*(H(J)+H(J+1))
UD(J):=H(J)
OD(J):=H(J+1)
INHOM(J):=3.0*(R(J+1)/H(J+1)-R(J)/H(J))TRID(UH,HD,OD,INHOM,N-2,LOES)J=1(1)N-2C(J+1):=LOES(J)C(1):=0.0
C(N):=0.0I=1(1)N-1A(I):=Y(I)
B(I):=R(I)/H(I)-H(I)*(C(I+1)+2.0*C(I))/3.0
D(I):=(C(I+1)-C(I))/3.0/H(I)(return)
Das Programm SPLVAL (SPLine VALue) berechnet den Interpolationswert
natürlicher kubischer Splines für ein beliebiges Argument
![]() .
.
OUTPUT-Parameter:
Im Fall FEHLER=1 kehrt das Programm SPLVAL ohne brauchbare Werte für YY, YYD und YYDD ins aufrufende Programm zurück.
Anmerkung:
Der erste Teil von SPLVAL, in dem der Index J jenes Intervalls bestimmt wird, zu welchem XX gehört, ist ein Zitat aus dem Programm LOCATE ([9], S. 111).
=15cm
Struktogramm 10SPLVAL(N,X,A,B,C,D,XX,YY,YYD,YYDD,FEHLER)EPS:=0.00001XX ![]() (X(1)-EPS) or XX
(X(1)-EPS) or XX ![]() (X(N)+EPS)(error 'Argument nicht im Interpolationsbereich')
(X(N)+EPS)(error 'Argument nicht im Interpolationsbereich')
FEHLER:=1
(return)......FEHLER:=0
JL:=0
JU:=N+1JU-JL ![]() 1JM:=(JU+JL)/2
XX
1JM:=(JU+JL)/2
XX ![]() X(JM)JL:=JMJU:=JMJ:=JLJ=0J:=1......J=NJ:=N-1......Z:=XX-X(J)
X(JM)JL:=JMJU:=JMJ:=JLJ=0J:=1......J=NJ:=N-1......Z:=XX-X(J)
YY:=((D(J)*Z+C(J))*Z+B(J))*Z+A(J)
YYD:=(3.0*D(J)*Z+2.0*C(J))*Z+B(J)
YYDD:=6.0*D(J)*Z+2.0*C(J)(return)
| x | y |
|
|
|
| |
|
| |
|
| |
|
|
|
|
mittels natürlicher kubischer Splines.
SPLINE liefert die folgenden Koeffizienten:
A B C D
1 0.2000 0.1628 0.0000 -1.8410
2 -0.1000 -1.8256 -3.3139 12.8117
3 -0.6000 -0.3547 8.2167 -8.9497
4 0.0000 1.9228 -2.5229 2.1024
Die entsprechende Interpolationsfunktion ![]() sowie die erste und zweite
Ableitung von
sowie die erste und zweite
Ableitung von ![]() sind in der Abbildung 3.3 dargestellt.
sind in der Abbildung 3.3 dargestellt.
Die Leistungsfähigkeit einer Interpolation mittels kubischer Splines, insbesondere was die Glattheit der Interpolationskurve betrifft, kann auch der Abb.3.1 entnommen werden (ausgezogene Kurve).
Das elektrische Potential in einem Atom kann in der sogenannten
'Hartree-Näherung' in der Form
Gleichung (3.12) läßt sich in der Form
Im folgenden soll nun ![]() für das Kalium-Atom berechnet werden
(Z=19), wobei
für das Kalium-Atom berechnet werden
(Z=19), wobei
![]() in Form einer Tabelle3.1 gegeben
ist:
in Form einer Tabelle3.1 gegeben
ist:
Radiale Elektronendichte fuer das Kalium-Atom. C. Froese-Fischer, Atomic Data 4, 301-399 (1972). Erste Spalte der Tabelle: Radius z in Bohr Zweite Spalte der Tabelle: z*z*rho(z) mit rho(z)=Wahrscheinlichkeitsdichte der Elektronen. Zahl der Tabellenwerte: 98 0.0000 0.0000000E+00 0.0001 0.4498521E-04 0.0002 0.1799408E-03 0.0004 0.7158627E-03 0.0006 0.1597434E-02 0.0008 0.2819985E-02 0.0010 0.4370591E-02 . . 10.0000 0.1369750E-02 11.0000 0.6779086E-03 12.0000 0.3228840E-03 13.0000 0.1491913E-03 14.0000 0.6738352E-04 15.0000 0.2994823E-04 16.0000 0.1283439E-04 17.0000 0.5481809E-05 18.0000 0.2320359E-05
Die numerische Auswertung der beiden in (3.13) enthaltenen
Integrale kann nun so erfolgen, daß man die Spline-Koeffizienten der
Stützpunkte
![]() (erstes Integral) bzw.
der Stützpunkte
(erstes Integral) bzw.
der Stützpunkte
![]() (zweites Integral
berechnet.
Bezeichnet man die zur ersten bzw. zweiten Funktion gehörenden
Spline-Koeffizienten mit
(zweites Integral
berechnet.
Bezeichnet man die zur ersten bzw. zweiten Funktion gehörenden
Spline-Koeffizienten mit ![]() bzw.
bzw. ![]() , so ergibt sich:
, so ergibt sich:
Man erhält somit für das erste Integral näherungsweise
![\begin{eqnarray*}
\sum_{i=1}^{J-1} \int_{z=z_{i}}^{z_{i+1}} dz \left[
A_{i}+B_...
...+B_{J}(z-z_{J})+C_{J}(z-z_{J})^{2}+
D_{J}(z-z_{J})^{3} \right]
\end{eqnarray*}](img432.gif)
![\begin{eqnarray*}
\int_{z=r}^{z_{J+1}} dz \left[ a_{J}+b_{J}(z-z_{J})+c_{J}(z-z...
...{i}+b_{i}(z-z_{i})+c_{i}(z-z_{i})^{2}+d_{i}(z-z_{i})^{3}\right]
\end{eqnarray*}](img433.gif)
r[Bohr] Zeff
=====================================
0.00 18.9999
0.25 9.1943
0.50 5.8019
0.75 4.0352
1.00 2.7497
1.50 1.3052
2.00 0.7475
2.50 0.5122
3.00 0.3805
4.00 0.2152
5.00 0.1152
7.00 0.0279
10.00 0.0025
14.00 0.0001
18.00 0.0001
Dieses Ergebnis ist physikalisch leicht zu interpretieren: in großer Kernnähe wirkt die Ladung des Kalium-Kerns mit Ihren 19 Elementarladungen ungestört. Entfernt man sich jedoch vom Kern, so kompensieren die Hüllenelektronen sukzessive die Kernladung. In einem größeren Abstand ist diese 'Abschirmung' der Kernladung total, und das Atom bietet sich als neutrales Gebilde dar.
Auch die Interpolation mit kubischen Splines ist kein fehlerfreies Verfahren. Wie die Abb. 3.2 (b) zeigt, kann es bei ungünstigen Stützpunkt-Verteilungen auch beim splining zu Oszillationen kommen.
Selbstverständlich gäbe es zum Thema Interpolation im allgemeinen und Spline-Interpolation im besonderen noch eine Menge Interessantes zu sagen. Ich muß mich hier auf einen knappen Themenkatalog beschränken. Einige dieser Themen werde ich in meiner ab dem SS 2002 angebotenen Lehrveranstaltung 'Ausgewählte Kapitel aus Numerische Methoden in der Physik' behandeln.
/usr/local/numeric/num_alg_c/... bzw. /usr/local/numeric/num_alg_f/...zur Verfügung.
Literatur: [10], S. 111ff, [2], S. 176/S. 399ff.
Zusätzlich zu den im vorigen Abschnitt erwähnten Programmen weise ich auf die folgenden Software-Produkte hin:
IMSL/MATH-LIBRARY
/csint Splines mit not-a-knot Randbedg.
/csdec Splines mit vom Benutzer gewählten Randbedg.
/cscon optisch glatte kubische Splinefunktion.
/csval Auswertung einer Splinefunktion
/csval Auswertung und Ableitung einer Splinefunktion.
Ein sehr umfangreiches Angebot bietet die 'Spline Toolbox' von MATLAB, über die Sie sich mittels der MATLAB-HELP-Funktion informieren können. Im folgenden finden Sie eine (unvollständige) Liste der angebotenen Funktionen sowie eine Kurzbeschreibung der Funktion csape:
![\includegraphics[scale=0.9]{num3_fig/spline1}](img13.png)
![\includegraphics[scale=0.9]{num3_fig/spline2}](img14.png)
Gegeben sei eine Menge von ![]() äquidistant verteilten
Stützpunkten
äquidistant verteilten
Stützpunkten
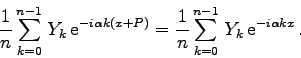
Selbstverständlich könnten die ![]() direkt aus dem linearen
Gleichungssystem (3.16) ermittelt werden. Im Falle der
Fourier-Entwicklung geht das aber sehr viel einfacher. Multipliziert man
nämlich die Glg. (3.16) mit
direkt aus dem linearen
Gleichungssystem (3.16) ermittelt werden. Im Falle der
Fourier-Entwicklung geht das aber sehr viel einfacher. Multipliziert man
nämlich die Glg. (3.16) mit
![]() und summiert über
den Index
und summiert über
den Index ![]() , so ergibt sich
, so ergibt sich
o.B.: der Ausdruck (A) hat im Falle
äquidistanter Stützpunkte das einfache Ergebnis
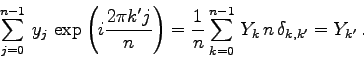
Man nennt die Auswertung (3.18), also die Berechnung der ![]() aus den
aus den
![]() , die Fourier-Transformation
(FT) der
, die Fourier-Transformation
(FT) der ![]() ; die Auswertung
von (3.16) heißt dementsprechend die inverse FT.
; die Auswertung
von (3.16) heißt dementsprechend die inverse FT.
Wegen der komplexwertigen Funktionenbasis der Fourier-Summe sind die
Fourierkoeffizienten ![]() im allgemeinen ebenfalls komplexwertig.
Ein in der Praxis wichtiger Sonderfall ist gegeben, wenn die Datenwerte
im allgemeinen ebenfalls komplexwertig.
Ein in der Praxis wichtiger Sonderfall ist gegeben, wenn die Datenwerte
![]() reell sind. In diesem Fall haben die Fourierkoeffizienten
die Eigenschaft3.4
reell sind. In diesem Fall haben die Fourierkoeffizienten
die Eigenschaft3.4
Die numerische Auswertung von (3.18) ist ein Prozess der Ordnung
![]() , d.h. es sind
, d.h. es sind ![]() Summenterme für jeden der
Summenterme für jeden der ![]() Koeffizienten zu
berechnen. Dies bedeutet für große
Koeffizienten zu
berechnen. Dies bedeutet für große ![]() einen sehr zeitintensiven
Rechenprozess.
einen sehr zeitintensiven
Rechenprozess.
In bezug auf die Rechenzeit bietet
die sogenannte Fast Fourier Transform FFT, die auf einer rekursiven
Berechnung der in (3.18) vorkommenden Summe beruht, einen
wesentlichen Fortschritt. Dieser Algorithmus, der auf den Ergebnissen einer
Arbeit von Danielson und Lanczos (1942) beruht, ist zwar im Prinzip einfach,
seine geschickte Programmierung ist jedoch im Detail etwas trickreich.
Er soll deshalb
hier nur prinzipiell erläutert werden, und zwar für das Beispiel von
![]() Stützpunkten. Spaltet man die Summe (3.18) in zwei Teilsummen
auf, und zwar in der Form
Stützpunkten. Spaltet man die Summe (3.18) in zwei Teilsummen
auf, und zwar in der Form
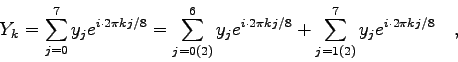
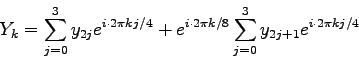
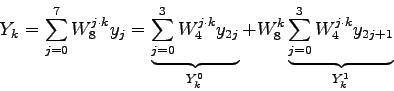
Die beiden Teilsummen ![]() und
und ![]() können nun ihrerseits
wieder zerlegt werden:
können nun ihrerseits
wieder zerlegt werden:
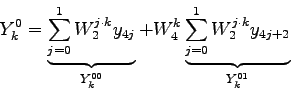
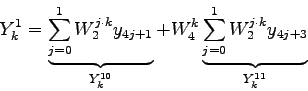
Die letzte Aufspaltung der vier Größen ![]() ,
, ![]() ,
,
![]() und
und ![]() lautet:
lautet:
Es sind somit die Fourierkoeffizienten 'auf die Ebene der ![]() -Werte
reduziert'. Davon ausgehend, kann der gewünschte Koeffizient
-Werte
reduziert'. Davon ausgehend, kann der gewünschte Koeffizient ![]() schrittweise aufgebaut werden, wie dies schematisch in der Abbildung
3.5 dargestellt ist.
schrittweise aufgebaut werden, wie dies schematisch in der Abbildung
3.5 dargestellt ist.
Die eben präsentierte Vorgangsweise funktioniert jedoch nur dann, wenn die
bei dem Aufbau der Koeffizienten gemäß Abb. 3.5
berücksichtigten Stützpunkte von Schritt zu Schritt verdoppelt werden
können, d.h. wenn die Stützpunktanzahl ![]() eine Potenz von
eine Potenz von ![]() ist
3.5.
ist
3.5.
Wie ebenfalls aus Abb. 3.5 hervorgeht, müssen die gegebenen
![]() -Werte
(
-Werte
(
![]() ) am Beginn der Kaskade (links in der Abb.) 'geeignet'
geordnet werden. Es zeigt sich, daß diese Indexordnung sich einfach
aus einer Bitumkehr der ursprünglichen Indizes in dualer Schreibweise
ergibt:
) am Beginn der Kaskade (links in der Abb.) 'geeignet'
geordnet werden. Es zeigt sich, daß diese Indexordnung sich einfach
aus einer Bitumkehr der ursprünglichen Indizes in dualer Schreibweise
ergibt:
| ursprüngliche Folge | Dual | BITUMKEHR | neue Folge |
| (Index) | (Index) | ||
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Der große Vorteil der FFT gegenüber der direkten Auswertung von
(3.18) liegt in der beträchtlichen Einsparung an Rechenzeit. Während
nämlich bei der Berechnung der Fourierkoeffizienten gemäß
(3.18) die Auswertung
von ![]() Summentermen nötig ist, reduziert sich diese Zahl bei der FFT
auf
Summentermen nötig ist, reduziert sich diese Zahl bei der FFT
auf ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
| . | . | . |
| . | . | . |
|
|
|
|
Bei sehr großen Datenmengen ist eine Fourier-Transformation mittels kleiner Computer (PC) überhaupt nur mittels der FFT möglich!
FFT-Programme sind häufig recht raffiniert programmiert. Es erscheint
im Rahmen dieser LV nicht sinnvoll, auf alle Details der Algorithmen
einzugehen. Aus diesem Grund werden im folgenden (ausnahmsweise) keine
Struktogramme, sondern direkt FFT-Programmlistings in den Sprachen C, F90
und MATLAB präsentiert. Es handelt sich dabei um
Programme zur schnellen Fourier-Transformation einer diskreten
komplexwertigen
Punktmenge mit ![]() Werten (
Werten (![]() = positive Integerzahl) und mit
äquidistanten
= positive Integerzahl) und mit
äquidistanten ![]() -Komponenten.
-Komponenten.
Quelle: [10], S. 507f.
INPUT-Parameter:
Die DATA-Werte müssen wie folgt abgespeichert sein:
RT{y0} DATA(1)
IT{y0} DATA(2)
RT{y1} DATA(3)
IT{y1} DATA(4)
.
.
RT{y(n-1)} DATA(2n-1)
IT{y(n-1)} DATA(2n)
DATA muß also mindestens ![]() Werte aufnehmen können!
Werte aufnehmen können!
#include <math.h>
#define SWAP(a,b) tempr=(a);(a)=(b);(b)=tempr
void four1(double data[], unsigned long nn, int isign)
{
unsigned long n,mmax,m,j,istep,i;
double wtemp,wr,wpr,wpi,wi,theta;
double tempr,tempi;
n=nn << 1;
j=1;
for (i=1;i<n;i+=2) {
if (j > i) {
SWAP(data[j],data[i]);
SWAP(data[j+1],data[i+1]);
}
m=n >> 1;
while (m >= 2 && j > m) {
j -= m;
m >>= 1;
}
j += m;
}
mmax=2;
while (n > mmax) {
istep=mmax << 1;
theta=isign*(6.28318530717959/mmax);
wtemp=sin(0.5*theta);
wpr = -2.0*wtemp*wtemp;
wpi=sin(theta);
wr=1.0;
wi=0.0;
for (m=1;m<mmax;m+=2) {
for (i=m;i<=n;i+=istep) {
j=i+mmax;
tempr=wr*data[j]-wi*data[j+1];
tempi=wr*data[j+1]+wi*data[j];
data[j]=data[i]-tempr;
data[j+1]=data[i+1]-tempi;
data[i] += tempr;
data[i+1] += tempi;
}
wr=(wtemp=wr)*wpr-wi*wpi+wr;
wi=wi*wpr+wtemp*wpi+wi;
}
mmax=istep;
}
}
#undef SWAP
/* (C) Copr. 1986-92 Numerical Recipes Software +. */
Quelle: [23], S. 322f.
INPUT-Parameter:
COMPLEX(KIND=KIND(0.0d0)) ,
das die komplexwertigen Größen enthält, die Fourier-transformiert
werden sollen.
SUBROUTINE fft(a,m,inv)
! Paul L. DeVries, Department of Physics, Miami University
! This subroutine performs the Fast Fourier Transform by
! the method of Cooley and Tukey
! start: 1965
! last modified: 1993
! Modifications H. Sormann: 2000
!
! Parameter description by H. Sormann 2000
! PARAMETERS: a vector of complex data which are to be
! Fourier-transformed
! this vector is VARIABLY dimensioned (see below)
! On return, a contains the FT coefficients.
!
! m 2**m is the number of data points
!
! inv equal 1 Fourier transform
! inv not equal 1 INVERSE Fourier transform
!
IMPLICIT NONE
INTEGER :: m,inv,n,nd2,i,j,k,l,le,le1,ip
COMPLEX(KIND=KIND(0.0d0)) :: u,w,t
COMPLEX(KIND=KIND(0.0d0)),DIMENSION(*) :: a ! * = var. dimension
DOUBLE PRECISION :: ang,pi
! PARAMETER (pi=3.141592653589793d0)
pi=4.d0*atan(1.d0)
n=2**m
nd2=n/2
j=1
DO i=1,n-1
IF(i .lt. j)THEN
t=a(j)
a(j)=a(i)
a(i)=t
ENDIF
k=nd2
100 IF(k .lt. j)THEN
j=j-k
k=k/2
goto 100
ENDIF
j=j+k
END DO
le=1
DO l=1,m
le1=le
le=le+le
u=(1.d0,0.d0)
ang=pi/dble(le1)
w=cmplx(cos(ang), -sin(ang),KIND(0.d0))
IF(inv .eq. 1)w=conjg(w)
DO j=1,le1
DO i=j,n,le
ip=i+le1
t=a(ip)*u
a(ip)=a(i)-t
a(i)=a(i)+t
END DO
u=u*w
END DO
END DO
IF(inv .ne. 1)THEN
DO i=1,n
a(i)=a(i)/dble(n)
END DO
ENDIF
END SUBROUTINE fft
Es gibt eine interne MATLAB-Routine mit dem Funktionsnamen fft.m. Wenn Sie sich mittels help fft über diese Routine informieren, erhalten Sie den folgenden Text:
%FFT Discrete Fourier transform. % FFT(X) is the discrete Fourier transform (DFT) of vector X. If the % length of X is a power of two, a fast radix-2 fast-Fourier % transform algorithm is used. If the length of X is not a % power of two, a slower non-power-of-two algorithm is employed. % For matrices, the FFT operation is applied to each column. % For N-D arrays, the FFT operation operates on the first % non-singleton dimension. % % FFT(X,N) is the N-point FFT, padded with zeros if X has less % than N points and truncated if it has more. % % FFT(X,[],DIM) or FFT(X,N,DIM) applies the FFT operation across the % dimension DIM. % % For length N input vector x, the DFT is a length N vector X, % with elements % N % X(k) = sum x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N. % n=1 % The inverse DFT (computed by IFFT) is given by % N % x(n) = (1/N) sum X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N. % k=1 % % The relationship between the DFT and the Fourier coeffs a and b in % N/2 % x(n)=a0+ sum a(k)*cos(2*pi*k*t(n)/(N*dt))+b(k)*sin(2*pi*k*t(n)/(N*dt)) % k=1 % is % a0 = X(1)/N, a(k) = 2*real(X(k+1))/N, b(k) = -2*imag(X(k+1))/N, % x is a length N discrete signal sampled at times t with spacing dt. % % See also IFFT, FFT2, IFFT2, FFTSHIFT. % Copyright (c) 1984-98 by The MathWorks, Inc. % $Revision: 5.9 $ $Date: 1998/06/30 18:43:41 $ % Built-in function.
Ein MATLAB-Programm, welches das Testproblem im Abschnitt 3.3.3 lösen soll, könnte etwa so aussehen:
%Eingabe der Testdaten von Skriptum:
n=8;
delta=1.0;
period=n*delta;
index=0:1:n-1;
werte=[0.7013+0.0437i -0.0724+0.5133i 0.0988-0.2688i 0.0715-0.1162i ...
0.4013+0.1188i -0.0901-0.1408i -0.1263-0.0688i 0.2660-0.3813i];
yy=fft(werte);
Nun folgt eine zwar im Prinzip harmlose, aber lästige Komplikation: wenn man die Ergebnisse der Fourier-Transformation mittels dieses Matlab-Programms mit den entsprechenden Resultaten des C-Programms four1.c bzw. des Fortran-Programms fft.f90 vergleicht, so erkennt man, daß die Reihenfolge der Fourierkoeffizienten bei Matlab sich von den anderen Ergebnissen unterscheidet (vgl. das Testbeispiel auf S. 83).
Das heißt nicht etwa, daß das Matlab-Programm falsch rechnet; die Ursache ist vielmehr, daß die Matlab-Version von einer zu Glg. (3.15) etwas verschiedenen - wenn auch mathematisch äquivalenten - Grundformel für die Interpolationsfunktion ausgeht.
Um nun alle daraus folgenden Unsicherheiten zu eliminieren, habe ich neue, sehr einfache Variationen der Matlab-Routinen fft.m bzw. ifft.m geschrieben, bei denen durch einfache Umordnungen der Fourierkoeffizienten dieses Problem nicht mehr auftritt:
function fourier = fft_sor(x)
% H. Sormann 20-9-2007
% last update 20-9-2007
% Um auch bei den Matlab-Programmen fft.m und ifft.m dieselbe
% Reihenfolge der Fourierkoeffizienten zu erhalten wie bei
% den im Skriptum praesentierten C-Programm (four1.c) bzw.
% F90-Programm (fft.f90), habe ich dieses einfache Programm
% geschrieben, bei welchem NACH der Anwendung von fft.m
% "automatisch" eine Umordnung der Matlab-Ergebnisse erfolgt.
% Wichtig ist, dass Sie die Programme fft_sor.m und ifft_sor.m
% paarweise verwenden, also nicht fft_sor.m mit ifft.m
% kombinieren und umgekehrt.
n=length(x);
d=fft(x);
fourier(1)=d(1);
for ind=2:n
fourier(ind)=d(n+2-ind);
end
function ifourier = ifft_sor(d)
% H. Sormann 20-9-2007
% last update 20-9-2007
% Um auch bei den Matlab-Programmen fft.m und ifft.m dieselbe
% Reihenfolge der Fourierkoeffizienten zu erhalten wie bei
% den im Skriptum praesentierten C-Programm (four1.c) bzw.
% F90-Programm (fft.f90), habe ich dieses einfache Programm
% geschrieben, bei welchem VOR der Anwendung von ifft.m
% "automatisch" eine Umordnung der Matlab-Ergebnisse erfolgt.
% Wichtig ist, dass Sie die Programme ifft_sor.m und fft_sor.m
% paarweise verwenden, also nicht ifft_sor.m mit fft.m
% kombinieren und umgekehrt.
n=length(d);
x(1)=d(1);
for ind=2:n
x(ind)=d(n+2-ind);
end
ifourier=ifft(x);
Dieses Beispiel beschreibt die Fourier-Transformation
der folgenden Testdaten (![]() ,
, ![]() ):
):
j RT{y(j)} IT{y(j)}
0 0.7013 0.0437
1 -0.0724 0.5133
2 0.0988 -0.2688
3 0.0715 -0.1162
4 0.4013 0.1188
5 -0.0901 -0.1408
6 -0.1263 -0.0688
7 0.2660 -0.3813
Die gegebenen Stützstellen repräsentieren somit eine periodische
Funktion mit der Periode ![]() , und das Programm FOUR1 liefert
die folgenden Fourierkoeffienten:
, und das Programm FOUR1 liefert
die folgenden Fourierkoeffienten:
k RT{Y(k)} IT{Y(k)}
0 1.2501 -0.3001
1 0.0001 0.3000
2 0.2601 0.0001
3 -0.7000 -0.7003
4 0.9001 -0.0501
5 0.9999 0.0000
6 2.0001 1.0001
7 0.9000 0.0999
Beachten Sie, daß das originale Matlab-Programm fft.m eine veränderte Reihenfolge der Fourierkoeffizienten ausgibt (s. die Diskussion auf Seite 82f):
k RT{Y(k)} IT{Y(k)}
0 1.2501 -0.3001
1 0.9000 0.0999
2 2.0001 1.0001
3 0.9999 -0.0000
4 0.9001 -0.0501
5 -0.7000 -0.7003
6 0.2601 0.0001
7 0.0001 0.3000
In diesem Abschnitt sollen als Beispiele für die vielfältigen Verwendungsmöglichkeiten der FT in der Physik, Meßtechnik etc. drei Anwendungsbereiche erläutert werden.
Wenn irgendein Signal mittels einer Meßapparatur registriert wird, wird in den meisten Fällen das ursprüngliche Signal durch die Eigenschaften der Meßapparatur verändert:

Für die konkrete Auswertung der Meßdaten ist es i. a. sehr wichtig, diesen Einfluß der Apparatur im nachhinein so gut als möglich zu eliminieren.
o. B.: Nennt man die Signalfunktion ![]() und die gemessene Funktion
und die gemessene Funktion ![]() , so ist der
Zusammenhang zwischen diesen Funktionen durch das sogenannte
Faltungsintegral
, so ist der
Zusammenhang zwischen diesen Funktionen durch das sogenannte
Faltungsintegral
Es soll nun angenommen werden, daß die Funktionen ![]() und
und
![]() periodisch bzgl. der Periode
periodisch bzgl. der Periode ![]() sind.
Außerdem soll angenommen werden, daß die Apparatefunktion
auf diese Periode beschränkt sei, d.h. daß gilt:
sind.
Außerdem soll angenommen werden, daß die Apparatefunktion
auf diese Periode beschränkt sei, d.h. daß gilt:
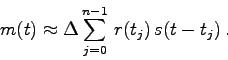
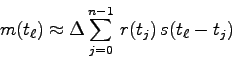
Nun kommt die FT ins Spiel! Setzt man nämlich für die drei in
Glg. (3.21) vorkommenden Größen ![]() ,
, ![]() und
und ![]() die entsprechenden
Fourierreihen gemäß (3.16) ein, so ergibt sich
die entsprechenden
Fourierreihen gemäß (3.16) ein, so ergibt sich
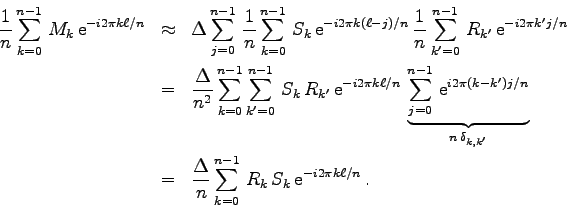
D. h.: Abgesehen von der Konstanten ![]() ist die
FT des Faltungsergebnisses
ist die
FT des Faltungsergebnisses ![]() einfach durch das Produkt der FT von
einfach durch das Produkt der FT von
![]() und
und ![]() gegeben.
Die Bedeutung von (3.22) für die Praxis ergibt sich daraus, daß
man diese Gleichung ohne Probleme nach der ungestörten Signalfunktion
auflösen kann:
gegeben.
Die Bedeutung von (3.22) für die Praxis ergibt sich daraus, daß
man diese Gleichung ohne Probleme nach der ungestörten Signalfunktion
auflösen kann:
Zur Demonstration dieser Anwendung der FT zeigt die Abbildung 3.6
die Testfunktion
![\includegraphics[scale=0.7]{num3_fig/dirichlet_1}](img17.png) |
Die entsprechenden Beträge der Fourierkoeffizienten für
![]() =128 sind in der Abb. 3.7 dargestellt.
Wie man deutlich sieht, wirken sich die statistischen Fehler so aus, daß
sich im 'mittleren Bereich' von
=128 sind in der Abb. 3.7 dargestellt.
Wie man deutlich sieht, wirken sich die statistischen Fehler so aus, daß
sich im 'mittleren Bereich' von ![]() (zum Unterschied von der glatten
Kurve) von Null verschiedene Fourierkoeffizienten zeigen. Es liegt daher
nahe, diese Koeffizienten dem noise zuzuschreiben und in geeigneter Weise
zu unterdrücken.
(zum Unterschied von der glatten
Kurve) von Null verschiedene Fourierkoeffizienten zeigen. Es liegt daher
nahe, diese Koeffizienten dem noise zuzuschreiben und in geeigneter Weise
zu unterdrücken.
![\includegraphics[scale=0.7]{num3_fig/dirichlet_2}](img18.png) |
Dies kann am einfachsten durch die Regel von Dirichlet geschehen, welche durch
Es ist natürlich klar, daß die Qualität der noise-Unterdrückung
entscheidend vom gewählten ![]() abhängt. In unseren Beispiel hat sich
abhängt. In unseren Beispiel hat sich ![]() als
sehr gute Wahl herausgestellt; allerdings muß zugegeben werden, daß die Kenntnis
der Idealkurve - die natürlich im Praxisfall nicht gegeben ist - diese Wahl sehr
erleichtert! Die hohe Qualität der Dirichlet-Glättung wird in der Abb. 3.8
demonstriert.
als
sehr gute Wahl herausgestellt; allerdings muß zugegeben werden, daß die Kenntnis
der Idealkurve - die natürlich im Praxisfall nicht gegeben ist - diese Wahl sehr
erleichtert! Die hohe Qualität der Dirichlet-Glättung wird in der Abb. 3.8
demonstriert.
![\includegraphics[scale=0.7]{num3_fig/dirichlet_3}](img19.png) |
Ausgangspunkt für die folgenden Überlegungen ist die Interpolationskurve
(3.15)
![\begin{displaymath}
I(t) = \frac{1}{n}\sum_{k=0}^{n-1} Y_{k}
\exp\left[-i...
...c{2\pi k t}{P}\right] =
\exp\left(-i 2\pi \nu_k t\right) .
\end{displaymath}](img524.gif)
Aus dieser Darstellung geht auch hervor, warum man diese Fourier-Transformation als Transformation aus dem Zeitraum in den Frequenzraum bezeichnet. Mathematisch völlig äquivalent ist auch die Transformation vom Ortsraum in den Wellenzahlraum.
Nun soll angenommen werden, daß nicht nur die gegebenen (gemessenen)
Werte ![]() , sondern die gesamte Funktion
, sondern die gesamte Funktion ![]() , welche 'hinter diesen
Werten steht', reell ist. In diesen Fall interessiert vor allem der Realteil der
Interpolationsfunktion, nämlich
, welche 'hinter diesen
Werten steht', reell ist. In diesen Fall interessiert vor allem der Realteil der
Interpolationsfunktion, nämlich
Die Antwort ist nein, und die Begründung dafür finden Sie in
der Abb. 3.9. Wegen der Periodizität der Interpolationsfunktion
sind auch die Fourierkoeffizienten ![]() periodisch, und zwar mit der
Periode
periodisch, und zwar mit der
Periode ![]() , d.h. es gilt:
, d.h. es gilt:
Man kann nun zeigen, daß jede zusammenhängende Gruppe von ![]() Fourierkoeffizienten mit den zugehörigen Frequenzen eine
Interpolationsfunktion durch die gegebenen Punkte ergibt, egal in welchem
Bereich der Frequenzachse diese Gruppe liegt. Natürlich erhält man dabei
jedesmal eine verschiedene Interpolationsfunktion!
Fourierkoeffizienten mit den zugehörigen Frequenzen eine
Interpolationsfunktion durch die gegebenen Punkte ergibt, egal in welchem
Bereich der Frequenzachse diese Gruppe liegt. Natürlich erhält man dabei
jedesmal eine verschiedene Interpolationsfunktion!
Wenn man nun fragt, welche der möglichen Interpolationen diejenige sein
wird, welche die geringste Neigung zur Oszillation zwischen den
Stützpunkten hat, so ist die Antwort einfach: natürlich jene,
welche die (dem Betrag nach) kleinsten Frequenzen enthält. Wenn man also
![]() Koeffizienten benötigt, wird der ideale Frequenzbereich um die
Frequenz Null liegen, also im Bereich
Koeffizienten benötigt, wird der ideale Frequenzbereich um die
Frequenz Null liegen, also im Bereich
![]() .
.
![\includegraphics[scale=0.7]{num3_fig/ideal_frequ}](img20.png)
|
Um diese ideale Interpolation formelmäßig darzustellen, bedarf es nur einer einfachen Umformung der Glg. (3.24):
![\begin{eqnarray*}
\Re\{I(t)\} = \sum_{k=-(n/2)+1}^{-1}
\left[
\Re\left\{\fr...
...{k}}{n}\right\} \sin\left(\frac{2\pi k t}{P}\right)
\right] .
\end{eqnarray*}](img532.gif)
![\begin{eqnarray*}
\Re\{I(t)\} = \sum_{k'=(n/2)+1}^{n-1}
\left[
\Re\left\{\f...
...{k}}{n}\right\} \sin\left(\frac{2\pi k t}{P}\right)
\right] .
\end{eqnarray*}](img534.gif)
Das heißt natürlich nicht, daß (3.26)-(3.28) die
(unbekannte) Funktion ![]() 'hinter den Stützpunkten' ideal
repräsentieren. Das geht schon daraus hervor, daß nur
diskrete Frequenzen mit einer Auflösung von
'hinter den Stützpunkten' ideal
repräsentieren. Das geht schon daraus hervor, daß nur
diskrete Frequenzen mit einer Auflösung von
Man kann also, was die Qualität einer Frequenzanalyse betrifft, wie folgt zusammenfassen:
Wenn das zu analysierende Signal eine Frequenz-Komponente
![]() enthält,
welche
außerhalb des Bereichs (3.30) liegt, kommt es zu einem störenden
Effekt, der darin besteht, daß die entsprechende Amplitude mit dem
Index
enthält,
welche
außerhalb des Bereichs (3.30) liegt, kommt es zu einem störenden
Effekt, der darin besteht, daß die entsprechende Amplitude mit dem
Index ![]() in den Nyquist-Bereich hineingespiegelt wird, d.h. es
wird eine Frequenz-Komponente
in den Nyquist-Bereich hineingespiegelt wird, d.h. es
wird eine Frequenz-Komponente
Im folgenden sollen die Zusammenhänge dieses Abschnittes an Hand eines Testbeispiels erläutert werden. Zu diesem Zweck definiert man eine analytische Funktion, die nur aus Cosinus- und Sinus-Termen besteht, und berechnet aus dieser Funktion eine Reihe von Werten, die man als Daten für eine Frequenz-Analyse mittels FT nimmt. Man erwartet, daß die FT-Analyse genau die Amplituden und Frequenzen der Testfunktion liefert.
Testfunktion:
Frequenz (Hz) cos-Ampl. sin-Ampl.
2 +2 --
4 -1 -3
7 -- +2
Die Periode der Testfunktion ist ![]() =1 s, und es wurden
=1 s, und es wurden ![]() =64 Stützpunkte
berechnet. Für die Frequenz-Analyse bedeutet das eine Frequenzauflösung
von
=64 Stützpunkte
berechnet. Für die Frequenz-Analyse bedeutet das eine Frequenzauflösung
von ![]() =1 Hz sowie einen Frequenzbereich von -31 bis +32 Hz
[s. Glgen. (3.29) und (3.30)].
=1 Hz sowie einen Frequenzbereich von -31 bis +32 Hz
[s. Glgen. (3.29) und (3.30)].
Wenn man dieses Problem mit Hilfe des Programms FOUR1 angeht (ohne die in diesem Abschnitt beschriebene Frequenz-Optimierung), erhält man das Ergebnis
Frequenz (Hz) RT(Y)/n IT(Y)/n
(cos) (sin)
2.000 1.0000 0.0000
4.000 -0.5000 -1.5000
7.000 -0.0000 1.0000
57.000 0.0000 -1.0000
60.000 -0.5000 1.5000
62.000 1.0000 0.0000
Die ersten drei Frequenzen sind korrekt, die drei letzten Ergebnisse liegen weit über den Testvorgaben. Dennoch ist die entsprechende Sin-Cos-Kurve eine Interpolationskurve [s. Abb. 3.11 (a)], allerdings kommt es zwischen den Stützpunkten zu starken Oszillationen.
Führt man jedoch die Frequenz-Optimierung im Sinne der Glgen. (3.26)-(3.28) durch, ergibt sich das Ergebnis
Frequenz (Hz) RT(Y)/n IT(Y)/n
(cos) (sin)
2.000 1.0000 0.0000
4.000 -0.5000 -1.5000
7.000 -0.0000 1.0000
-7.000 0.0000 -1.0000
-4.000 -0.5000 1.5000
-2.000 1.0000 0.0000
Dieses Resultat entspricht exakt der Testvorgabe, und zwar sowohl in bezug
auf die Frequenzen als auch in bezug auf die Amplituden. So werden z.B.
zwei Cosinusse angezeigt, jeweils mit der Amplitude 1.000, und mit den
Frequenzen +2 und -2. Das bedeutet:
Die entsprechende Interpolationsfunktion [s. Abb. 3.11 (b)] entspricht genau der Testkurve.
![\includegraphics[scale=0.8]{num3_fig/four8}](img22.png) |
Zum Abschluß soll noch der aliasing effect demonstriert werden.
Angenommen, die Testfunktion laute
Frequenz (Hz) RT(Y)/n IT(Y)/n
(cos) (sin)
2.000 1.0000 0.0000
4.000 -0.5000 -1.5000
9.000 0.0000 -1.0000
-9.000 -0.0000 1.0000
-4.000 -0.5000 1.5000
-2.000 1.0000 0.0000
Wie Sie sehen, werden die ersten drei Terme der Testfunktion exakt
erhalten, der letzte Term mit seinen 55 Hz scheint hingegen nicht auf.
Statt dessen wird eine Frequenz von ![]() 9 Hz angezeigt, die in der
Testfunktion nicht vorkommt. Ein typischer aliasing effect
s. Glg. (3.31)] wegen
9 Hz angezeigt, die in der
Testfunktion nicht vorkommt. Ein typischer aliasing effect
s. Glg. (3.31)] wegen
Wie auch in anderen Kapiteln dieses Skriptums muß ich mich auch bei der FT auf die wichtigsten Grundlagen beschränken. Auch hier möchte ich versuchen, Ihnen weitere - insbesondere für die Anwendung - wichtige Themen in meiner LV im SS Ausgewählte Kapitel aus 'Numerische Methoden in der Physik' zu vermitteln:
Da die Fourierentwicklung eine außerordentlich wichtige Methode darstellt, mathematische und physikalische Probleme zu behandeln, ist das Angebot an einschlägigen Programmen besonders groß. Ich kann daher im folgenden nur sehr allgemeine Informationen geben:
/usr/local/numeric/numrec/c bzw. /usr/local/numeric/num_alg/c
Ein Beispiel: Smoothing of noised data by convolution with a kernel:3.6
data=Table[N[Bessel][1,10 n/256] + 0.2 (Random[]-1/2)],{n,256}];
kern=Table[N[Exp[-200 (n/256)^2]],{n,256}];
conv=InverseFourier[Fourier[data]/Fourier[kern]];
ListPlot[Chop[conv]]
Vergessen Sie bitte nicht meinen Rat, anstelle dieser Routinen die von mir variierten Programme fft_sor bzw. ifft_sor zu verwenden.
Weitere Fourier-Transform-Programme von MATLAB:
| fft2 | zweidim. Fast-Fourier-Transform |
| ifft2 | inverse zweidimensionale FFT |
| fftshift | Programm zur Frequenzverschiebung (vgl. Abschnitt 3.4.3). |