Nächste Seite: Numerische Lösung von transzendenten Aufwärts: Numerische Methoden in der Vorherige Seite: Interpolation von Punktmengen.
So leistungsfähig die Methode der Interpolation in vielen Fällen auch sein mag, gibt es doch sehr häufig Approximationsprobleme, bei welchen die gegebene Punktmenge keine glatte Funktion repräsentiert. Dies trifft vor allem dann zu, wenn die Stützpunktkoordinaten statistisch fehlerbehaftet sind, weil sie z.B. Ergebnisse experimenteller Messungen darstellen.
Betrachtet man beispielsweise die Bestimmung des Widerstandswertes ![]() eines
metallischen Leiters mittels der Versuchsanordnung Abb.4.1,
so erhält man ein Spannungs-Strom-Diagramm der Art Abb.4.2.
eines
metallischen Leiters mittels der Versuchsanordnung Abb.4.1,
so erhält man ein Spannungs-Strom-Diagramm der Art Abb.4.2.
Der Zusammenhang zwischen Spannung und Strom ist offenbar ein linearer:
es gilt das Ohm'sche Gesetz
Die in einem solchen Fall anzuwendende Approximationsfunktion muß also eine Gerade (ein Polynom ersten Grades) sein. Es ist klarerweise völlig sinnlos, hier eine Interpolationsfunktion dazu zu zwingen, genau durch alle Meßpunkte hindurchzugehen. Es ist im Gegenteil eine Glättung ohne übermäßige Berücksichtigung von Fehlmessungen erwünscht.
Es soll durch ![]() gegebene Punkte (
gegebene Punkte (
![]() ) eine Kurve
) eine Kurve ![]() gelegt werden, die den Punkten möglichst nahekommt, wobei jedoch die
auftretenden Meßunsicherheiten ausgeglichen werden sollen.
Zusätzlich soll es noch möglich sein, den Einfluß der einzelnen Meß
punkte
auf
gelegt werden, die den Punkten möglichst nahekommt, wobei jedoch die
auftretenden Meßunsicherheiten ausgeglichen werden sollen.
Zusätzlich soll es noch möglich sein, den Einfluß der einzelnen Meß
punkte
auf ![]() durch Gewichtsfaktoren zu verändern.
durch Gewichtsfaktoren zu verändern.
Diese Forderungen lassen sich mathematisch folgendermaßen formulieren (Grundgleichung der Least-Squares (LSQ) Approximation):
Die Summe der gewichteten Fehlerquadrate zwischen den gegebenen und den approximierten Funktionswerten soll ein Minimum werden. Die Bedeutung der Gewichtsfaktoren wird vor allem dann klar, wenn man sich für die statistische Auswertung von Punktmengen interessiert. Davon wird im nächsten Abschnitt dieses Kapitels die Rede sein.
Die Modellfunktion ![]() dient in vielen Fällen nicht bloß dazu, 'eine schöne
Kurve zu formen', sondern oft haben die Modellparameter auch eine konkrete
physikalische Bedeutung.
dient in vielen Fällen nicht bloß dazu, 'eine schöne
Kurve zu formen', sondern oft haben die Modellparameter auch eine konkrete
physikalische Bedeutung.
Die LSQ-Methode beruht auf dem Vergleich von (meist) experimentell ermittelten
Meßwerten ![]() mit den entsprechenden Modellwerten
mit den entsprechenden Modellwerten
![]() .
Es ist evident,daß die Qualität der Ergebnisse (Fit-Parameter) sehr von der
statistischen Qualität der
.
Es ist evident,daß die Qualität der Ergebnisse (Fit-Parameter) sehr von der
statistischen Qualität der ![]() -Werte abhängen wird.
-Werte abhängen wird.
Angenommen, eine Messung wurde unter genau denselben Bedingungen ![]() mal
wiederholt. Als Meßwerte für
mal
wiederholt. Als Meßwerte für ![]() wurden dabei die (i.a.)
verschiedenen Werte
wurden dabei die (i.a.)
verschiedenen Werte
![]() erhalten. Trägt man diese Werte in ein Diagramm ein (vgl. Abb.4.3),
so erhält man eine Punktmenge, die um den Erwartungswert
erhalten. Trägt man diese Werte in ein Diagramm ein (vgl. Abb.4.3),
so erhält man eine Punktmenge, die um den Erwartungswert ![]() oder
Mittelwert der Messung verteilt ist:
oder
Mittelwert der Messung verteilt ist:
Ein Maß für die Streuung der einzelnen Meßwerte um den
Erwartungswert ist die Standardabweichung
In sehr vielen praktischen Fällen ist die Wahrscheinlichkeit ![]() , mit
der eine bestimmte Abweichung des Meßwertes vom Erwartungswert
, mit
der eine bestimmte Abweichung des Meßwertes vom Erwartungswert ![]() auftritt,
durch die Wahrscheinlichkeitskurve
auftritt,
durch die Wahrscheinlichkeitskurve
Der schraffierte Bereich in Abb.4.5 bedeutet offenbar jene
Wahrscheinlichkeit, mit der ein Meßwert im Intervall
![]() liegt. Diese Wahrscheinlichkeit beträgt
liegt. Diese Wahrscheinlichkeit beträgt
Normalverteilungen sind typisch für Meßvorgänge, bei denen die Meß größe - zumindest innerhalb eines gewissen Intervalls - jeden beliebigen Wert annehmen kann (analoge Meßvorgänge). Die für digitale Meßvorgänge typische Poisson-Verteilung wird im nächsten Abschnitt diskutiert.
Da diese LV. keine Statistik-Vorlesung ist, müssen die folgenden Überlegungen zwangsläufig ohne die an und für sich notwendigen Beweisführungen präsentiert werden.
Man berechnet zuerst die sogenannte Normalmatrix ![]() mit den
Koeffizienten
mit den
Koeffizienten
Durch Invertierung der Normalmatrix erhält man die
Kovarianzmatrix ![]() :
:
Die Kovarianzmatrix enthält zwei wichtige Informationen: einerseits
stellen ihre Diagonalelemente die Quadrate der Standardabweichungen der
Fit-Parameter dar, also
andererseits ergeben sich aus ![]() die Korrelationskoeffizienten
die Korrelationskoeffizienten ![]() zwischen den Fit-Parametern:
zwischen den Fit-Parametern:
Die ![]() -Werte, die stets im Intervall
-Werte, die stets im Intervall ![]() liegen, geben eine
Information darüber, wie stark der
liegen, geben eine
Information darüber, wie stark der ![]() -te und der
-te und der ![]() -te Fit-Parameter
einander beeinflussen.
-te Fit-Parameter
einander beeinflussen.
![]() ist im Falle eines idealen Modells und für
ist im Falle eines idealen Modells und für ![]() approximativ
normalverteilt mit dem Mittelwert 1 und der Standardabweichung
approximativ
normalverteilt mit dem Mittelwert 1 und der Standardabweichung ![]() .
Die Größe
.
Die Größe ![]() (Anzahl der Stützpunkte minus Anzahl der
Fit-Parameter) wird als die Anzahl der Freiheitsgrade bezeichnet.
(Anzahl der Stützpunkte minus Anzahl der
Fit-Parameter) wird als die Anzahl der Freiheitsgrade bezeichnet.
Die Varianz eines Fits kann als Indikator für die Güte der verwendeten
Modellfunktion dienen: wenn ![]() signifikant außerhalb des
Intervalles
signifikant außerhalb des
Intervalles
![]() liegt, paßt das Modell nicht gut
zur gegebenen Punktmenge.
liegt, paßt das Modell nicht gut
zur gegebenen Punktmenge.
Die statistische Auswertung eines LSQ-Problems setzt
voraus, daß man die Standardabweichungen ![]() der Einzelwerte
kennt. Woher bekommt man diese
der Einzelwerte
kennt. Woher bekommt man diese ![]() -Werte?
-Werte?
Für die Praxis sind vor allem die folgenden beiden Fälle von Bedeutung:
Wie bereits erläutert, kommt diese Situation in der experimentellen
Praxis sehr häufig vor. In diesem Fall gilt meistens wenigstens approximativ,
daß die ![]() 's aller Meßwerte gleich sind, daß also
's aller Meßwerte gleich sind, daß also
Zählexperimente spielen z.B. in der Kernphysik eine dominierende Rolle. Die Versuchsanordnungen entsprechen dabei dem Schema

Dabei könnte A ein radioaktives Präparat sein, D ein Strahlendetektor, Z ein Digitalzähler und T eine Uhr.
Ohne auf die Theorie der Poisson-Statistik näher einzugehen, soll hier nur die wichtigste Eigenschaft dieser Statistik erwähnt werden:
Bei einer Poisson-Verteilung ist für jeden Meßwert sein Erwartungswert ![]() mit der entsprechenden Standardabweichung
mit der entsprechenden Standardabweichung ![]() über die einfache
Beziehung
über die einfache
Beziehung
Unter einer Modellfunktion mit linearen Parametern versteht man eine
Form
Setzt man ein Modell (4.12) in die LSQ-Grundgleichung (4.1) ein, so
erhält man
![\begin{displaymath}\chi^{2}=\sum_{k=1}^{n} g_{k} \left[ y_{k}-\sum_{j=1}^{m} a_{...
...{j}(x_{k}) \right]^{2} \quad \rightarrow \quad \mbox{Minimum!} \end{displaymath}](img604.gif)
![\begin{displaymath}\frac{\partial\chi^{2}}{\partial a_{i}} = \sum_{k=1}^{n}
g_{...
...{j} \varphi_{j}(x_{k})
\right] = 0 \quad i=1,\ldots,m \quad . \end{displaymath}](img605.gif)
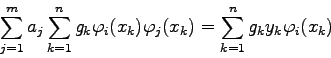
Für lineare Modellfunktionen (4.12) ist die Aufstellung der
Normalmatrix gemäß (4.6) sehr einfach; es gilt nämlich:
Im Abschnitt 4.3.2 wurde (ohne Beweisführung) angegeben, daß sich die
Standardabweichungen
der Fitparameter aus den Diagonalelementen der Kovarianzmatrix
ergeben [Glg. (4.8)]
Dieser Sachverhalt soll im folgenden an Hand eines sehr einfachen Modells
demonstriert werden, nämlich mittels einer linearen Regression mit
der Modellfunktion
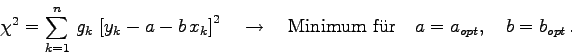
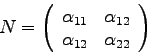
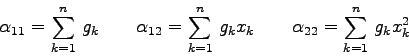
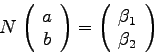
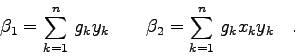
Die Kovarianzmatrix ![]() ist die Inverse der Normalmatrix, also
ist die Inverse der Normalmatrix, also
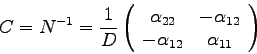
Die Berechnung dieser Standardabweichungen kann aber auch auf eine andere Art geschehen, nämlich auf der Basis des Fehlerfortpflanzungsgesetzes (FFG).
Es ist klar, daß die optimierten Parameter ![]() und
und ![]() Funktionen
aller
Funktionen
aller ![]() und
und ![]() Komponenten der gegebenen Punkte sind, also
Komponenten der gegebenen Punkte sind, also
![\begin{displaymath}
\sigma_{a}^{2}=\sum_{l=1}^{n}\left[
\left(\frac{\partial a...
...ial a}{\partial y_{l}}\right)^{2} \sigma(y_{l})^{2}
\right]
\end{displaymath}](img626.gif)
![\begin{displaymath}
\sigma_{b}^{2}=\sum_{l=1}^{n}\left[
\left(\frac{\partial b...
...ial b}{\partial y_{l}}\right)^{2} \sigma(y_{l})^{2}
\right]
\end{displaymath}](img627.gif)
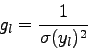
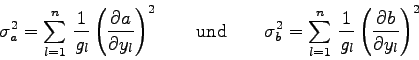
![\begin{displaymath}
\sigma_{a}^{2}=\sum_{l=1}^{n} \frac{1}{g_{l}}
\left[\frac...
...lpha_{22} g_{l} - \alpha_{12} g_{l} x_{l}\right)
\right]^{2}
\end{displaymath}](img633.gif)
![\begin{displaymath}
\sigma_{b}^{2}=\sum_{l=1}^{n} \frac{1}{g_{l}}
\left[\frac...
...lpha_{12} g_{l} + \alpha_{11} g_{l} x_{l}\right)
\right]^{2}
\end{displaymath}](img634.gif)
![\begin{displaymath}
\sigma_{a}^{2}=\frac{1}{D^{2}}\sum_{l=1}^{n} g_{l}
\left[\alpha_{22}-\alpha_{12} x_{l}\right]^{2}
\end{displaymath}](img635.gif)
![\begin{displaymath}
=\frac{1}{D^{2}}\sum_{l=1}^{n}\sum_{k=1}^{n}\sum_{k'=1}^{n}...
...} - 2 x_{l} x_{k}^{2} x_{k'} +
x_{l}^{2} x_{k} x_{k'}\right]
\end{displaymath}](img636.gif)
![\begin{displaymath}
\sigma_{a}^{2}=\frac{1}{D^{2}}\sum_{l,k,k'} g_{l}g_{k}g_{...
...k'}^{2} -
\left(\sum_{l=1}^{n} g_{l}x_{l}\right)^{2}\right]
\end{displaymath}](img638.gif)
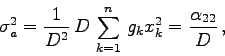
Eine ganz ähnliche Rechnung kann auch für ![]() durchgeführt
werden.
durchgeführt
werden.
Quelle: [9], S.513ff, [10], S. 674ff mit Änderungen.
INPUT-Parameter:
OUTPUT-Parameter:
von LFIT benötigte Prozeduren:
void funcs(double x, double afunc[], int ma)
{ ..... Definition lokaler Variabler .....
afunc[1]= ..... phi_{1}(x);
.
.
afunc[ma] = ..... phi_{m}(x);
}
Programmstruktur:
=15cm
Struktogramm 11LFIT(X,Y,SIG,NDATA,MA,A,YF,COVAR,CHISQ)I=1(1)MAJ=1(1)MANORMAL(I,J):=0.0BETA(I):=0.0K=1(1)NDATAFUNCS(X(K),AFUNC,MA)G:=1.0/SIG(K)/SIG(K)I=1(1)MAJ=1(1)INORMAL(I,J):=NORMAL(I,J) + G*AFUNC(I)*AFUNC(J)BETA(I):=BETA(I) + G*Y(K)*AFUNC(I)I=2(1)MAJ=1(1)I-1NORMAL(J,I):=NORMAL(I,J)LUDCMP(NORMAL,MA,INDX,D,KHAD)
LUBKSB(NORMAL,MA,INDX,BETA,LOES)J=1(1)MAA(J):=LOES(J)CHISQ:=0.0K=1(1)NDATAFUNCS(X(K),AFUNC,MA)G:=1.0/SIG(K)/SIG(K)
SUM:=0.0J=1(1)MASUM:=SUM + A(J)*AFUNC(J)YF(K):=SUM
CHISQ:=CHISQ + G*(Y(K)-SUM)*(Y(K)-SUM)J=1(1)MAI=1(1)MABETA(I):=0.0BETA(J):=1.0LUBKSB(NORMAL,MA,INDX,BETA,LOES)I=1(1)MACOVAR(I,J):=LOES(I)(return)
Anmerkungen zu LFIT:
In diesem Fall ist natürlich keine Aussage über die Varianz des Fits bzw. über die Statistik der optimierten Modellparameter möglich.
Die Anwendung der Prozedur LFIT kann z.B. im Rahmen des folgenden Hauptprogrammes erfolgen:
=15cm
Programmschema:Eingabe: 1) die NDATA Stuetzpunkte X(), Y() sowie die SD SIG().
2) Anzahl MA der Modellterme.LFIT(X,Y,SIG,NDATA,MA,A,YF,COVAR,CHISQ)VAR:=CHISQ/(NDATA-MA)I=1(1)MASDPAR(I):=SQRT(COVAR(I,I))I=1(1)MA-1J=I+1(1)MANORM:=SQRT(COVAR(I,I)*COVAR(J,J))NORM ne 0.0COVAR(I,J):=COVAR(I,J)/NORM
COVAR(J,I):=COVAR(I,J)......I=1(1)MACOVAR(I,I) ne 0.0COVAR(I,I):=1.0......Ausgabe: 1) die Varianz VAR.
2) die optimierten Parameter A().
3) die Standardabweichungen der Parameter SDPAR().
4) die normierte Kovarianzmatrix COVAR(,).
5) eventuell: Tabelle X() Y() YF()(return)
Für diesen Test wurden 101 Stützpunkte berechnet, die um ihre jeweiligen
Erwartungswerte normalverteilt sind, wobei ein konstantes ![]() für
alle Punkte angenommen wurde.
für
alle Punkte angenommen wurde.
Die Erwartungswerte aller Punkte liegen exakt auf der Polynomkurve dritten
Grades
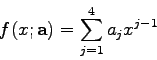
Dementsprechend lautet die von LFIT aufgerufene Prozedur FUNCS z.B. in C wie folgt:
void funcs(double x, double afunc[], int ma)
{ int i;
afunc[1]=1.0;
for(i=2;i<=ma;i++) afunc[i]=afunc[i-1]*x;
}
Für den ersten Datensatz wurde eine Normalverteilung
mit ![]() simuliert.
simuliert.
Interpretation der Tabelle 4.1 (a):
Je nach der Anzahl der Modellterme beträgt die Anzahl der Freiheitsgrade
zwischen 96 und 100. Dementsprechend sollte sich für ein gutes Modell
gemäß (4.10) eine Varianz zwischen ca. ![]() und ca.
und ca. ![]() ergeben.
ergeben.
Wegen der relativ großen Streuung der Stützpunkte
[vgl. Abb.4.6 (a)]
ist eine Unterscheidung darüber, ob das ideale Modell ein Polynom 2. oder
3. Grades ist, nicht möglich! Diese Unsicherheit wirkt sich
auch darin aus, daß die ![]() 's der gefitteten Parameter ab MA=4 oft
größer sind als die Beträge der entsprechenden Parameter-Mittelwerte,
die auch für das an und für sich richtige Polynom 3. Grades sehr schlecht
zu den simulierten Parametern
's der gefitteten Parameter ab MA=4 oft
größer sind als die Beträge der entsprechenden Parameter-Mittelwerte,
die auch für das an und für sich richtige Polynom 3. Grades sehr schlecht
zu den simulierten Parametern ![]() passen:
passen:
|
|
|
|
|
|
|
|
|
|
|
|
Die Situation wird natürlich viel besser, wenn die Stützpunkte eine
bessere Statistik haben.
Für den zweiten Datensatz wurde angenommen: ![]() .
.
Interpretation der Tabelle 4.1 (b):
Hier ist die Bestimmung des idealen Modells sehr viel leichter. Die
Polynome nullten, ersten und zweiten Grades haben eine zu hohe Varianz,
und erst ab MA![]() 4 sind die Modellfunktionen als gut zu bezeichnen.
Da aber für MA
4 sind die Modellfunktionen als gut zu bezeichnen.
Da aber für MA![]() 4 einige Fit-Parameter 'in ihren
4 einige Fit-Parameter 'in ihren ![]() 's untergehen',
ist das Polynom dritten Grades die beste Modellfunktion
[s. Abb.4.7 (b)].
's untergehen',
ist das Polynom dritten Grades die beste Modellfunktion
[s. Abb.4.7 (b)].
Tabelle 4.1 (a):
| MA | Varianz | optimierte Parameter | Anmerkungen |
|
|
|
|
schlechtes Modell |
|
|
|
|
an der Grenze |
|
|
|||
|
|
|
|
|
|
|
gutes Modell | ||
|
|
|||
|
|
|
|
|
|
|
gutes Modell, | ||
|
|
schlechte Statistik | ||
|
|
s. Abb.4.6 | ||
|
|
|
|
|
|
|
gutes Modell | ||
|
|
schlechte Statistik | ||
|
|
|||
|
|
Tabelle 4.1 (b):
| MA | Varianz | optimierte Parameter | Anmerkungen |
|
|
|
|
schlechtes Modell |
|
|
|
|
schlechtes Modell |
|
|
|||
|
|
|
|
|
|
|
schlechtes Modell | ||
|
|
|||
|
|
|
|
gutes Modell |
|
|
Fit-Parameter haben | ||
|
|
günstige |
||
|
|
siehe Abb.4.6 | ||
|
|
|
|
gutes Modell, |
|
|
aber manche Fit-Parameter | ||
|
|
haben sehr schlechte Statistik. | ||
|
|
'mixing of parameters' | ||
|
|
Setzt man die Modellfunktion
![\begin{displaymath}\chi^{2}=\sum_{k=1}^{n} g_{k} \left[y_{k}-a \cdot e^{-bx_{k}} \right]^{2}
\quad \rightarrow \quad \mbox{Minimum!} \end{displaymath}](img706.gif)
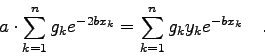
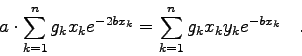
Aus diesem einfachen Beispiel ist bereits zu ersehen, daß man bei nicht-linearen Modellfunktionen mit dem im Abschnitt 4.4 beschriebenen Verfahren nicht weiterkommt. Eine Möglichkeit der Behandlung nicht-linearer Modelle im Rahmen der LSQ Approximation stellt der im Abschnitt 4.5.3 behandelte Gauss-Newton Formalismus dar.
Vorher soll aber noch gezeigt werden, wie man bestimmte nicht-lineare Modellfunktionen auf einfache Weise linearisieren kann.
Eine in der Praxis häufig vorkommende Meßpunkt-Verteilung ist in der
Abb.4.7 dargestellt. Die
![]() -Werte gehorchen offenbar
einem Exponentialgesetz. Ihre Verteilung in einem
halblogarithmischen
-Werte gehorchen offenbar
einem Exponentialgesetz. Ihre Verteilung in einem
halblogarithmischen
![]() -Koordinatensystem ist daher annähernd linear.
-Koordinatensystem ist daher annähernd linear.
Für die so verteilten Punkte kommt als Modellfunktion offenbar
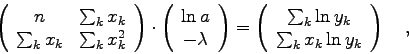
![\includegraphics[scale=0.9]{num4_fig/lsq8}](img30.png) |
Dieses System ist einfach zu lösen und man erhält
Dazu ein Beispiel: Die in Abb.4.7 dargestellten 7 Punkte haben die Koordinaten
| x: | |
|
|
|
|
|
|
| y: | |
|
|
|
|
|
|
Daraus erhält man unter Anwendung von (4.18)
Anmerkungen:
In [7], S.330ff findet man eine Reihe weiterer Beispiele zur Linearisierung einfacher nicht-linearer Modellfunktionen.
Abschließend noch ein Hinweis: vermeiden Sie in Ihren
Modellfunktionen
'versteckte Korrelationen' zwischen Fit-Parametern. So ist z. B. das Modell
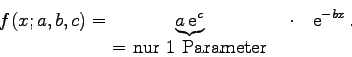
In all jenen Fällen, in denen eine Linearisierung der Modellfunktion im Sinne des Abschnitts 4.5.2 nicht möglich ist oder nicht gewünscht wird, empfiehlt sich die folgende Vorgangsweise:
Ausgangspunkt ist die völlig allgemeine Modellfunktion
![\begin{displaymath}
\chi^{2}=\sum_{k=1}^{n} g_{k} \left[ y_{k}-f(x_{k};{\bf a})\right]^{2} \end{displaymath}](img746.gif)
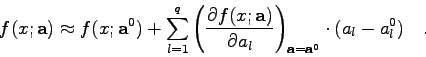
![\begin{displaymath}\chi^{2} = \sum_{k=1}^{n} g_{k} \left[ y_{k} - f(x_{k};{\bf a...
...bf a}={\bf a}^{0}} \cdot (a_{l}-a_{l}^{0}) \right]^{2} \quad , \end{displaymath}](img750.gif)
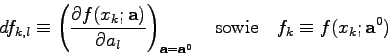
![\begin{displaymath}\frac{\partial \chi^{2}}{\partial a_{j}} = -2 \sum_{k=1}^{n} ...
...=1}^{q} df_{k,l} (a_{l}-a_{l}^{0}) \right]
\cdot df_{k,j} = 0 \end{displaymath}](img752.gif)
Die Iteration wird abgebrochen, wenn alle Parameter die
relative Genauigkeitsabfrage
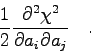
![\begin{displaymath}
\frac{1}{2} \frac{\partial^{2}\chi^{2}}{\partial a_{i} \par...
...};{\bf a})}
{\partial a_{i}\partial a_{j}}
\right]
\quad . \end{displaymath}](img764.gif)
Eine primäre Forderung für die praktische Verwendbarkeit numerischer Verfahren, insbesondere iterativer Verfahren, ist die nach deren Stabilität. Es muß gewährleistet sein, daß das Verfahren konvergiert, und zwar auch dann, wenn die Anfangswerte der Iteration ungünstig gewählt wurden.
Im folgenden Testbeispiel wird nun gezeigt, daß das GN-Verfahren diese Forderung keineswegs erfüllt.
Ausgangspunkt für diesen Test ist die Funktion
10 Datenwerte:
X Y=F(X)
1 .1000000E+01 .3530524E+01
2 .2000000E+01 .1864185E+01
3 .3000000E+01 .1116885E+01
4 .4000000E+01 .6767378E+00
5 .5000000E+01 .4104280E+00
6 .6000000E+01 .2489355E+00
7 .7000000E+01 .1509869E+00
8 .8000000E+01 .9157819E-01
9 .9000000E+01 .5554498E-01
10 .1000000E+02 .3368973E-01
Faßt man diese Daten als Stützpunkt-Koordinaten für eine LSQ-Problem
mit (4.24) als Modellfunktion auf, so sollte das Iterationsergebnis
des GN-Prozesses natürlich lauten:
Im folgenden wird nun das Konvergenzverhalten eines Programms, das auf dem
im Abschnitt 4.5.3 erläuterten Algorithmus beruht, untersucht. Zu diesem
Zweck wurde von verschiedenen guessed values für die ![]() und
und
![]() ausgegangen, während für
ausgegangen, während für ![]() und
und ![]() stets die
Startwerte
stets die
Startwerte ![]() und
und ![]() gewählt wurden.
gewählt wurden.
Die Ergebnisse dieses Tests sind in der
Abb.4.8 zusammengefaßt.
Diese Testergebnisse sind natürlich sehr unbefriedigend! Es ist nämlich in der Praxis äußerst schwierig, den Konvergenzbereich abzuschätzen. Die Methode, die guessed values für die Parameter-Startwerte solange zu variieren, bis die Iteration endlich einmal klappt, ist inakzeptabel!
Einen Ausweg aus diesem Dilemma wurde 1963 von D.W. Marquardt gefunden 4.1. Im folgenden werden die Ergebnisse seiner Untersuchungen präsentiert, ohne auf die mathematische Beweisführung einzugehen.
Ausgangspunkt für die Variation des GN-Verfahrens nach Marquardt ist das lineare Gleichungssystem (4.20):
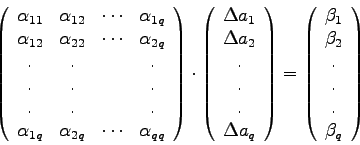
Gleichungssysteme dieser Art sind also im Rahmen des GM-Algorithmus zu
lösen. Nach der Variation von Marquardt löst man statt dessen das
System
Angenommen, der ![]() -te Iterationsschritt während des GN-Prozesses habe die
Fehlerquadratsumme
-te Iterationsschritt während des GN-Prozesses habe die
Fehlerquadratsumme ![]() ergeben. Der darauffolgende
Iterationsschritt liefere den Wert
ergeben. Der darauffolgende
Iterationsschritt liefere den Wert
![]() .
.
Es kann nun ohne weiteres geschehen, daß gilt:
Die allgemeingültige Aussage, die Marquardt streng mathematisch bewiesen hat,
lautet nun:
Es ist immer möglich, die in (4.25) vorkommende Größe
![]() so zu wählen, daß gilt:
so zu wählen, daß gilt:
Damit ist aber die Konvergenz des Verfahrens gesichert.
Um die Wirkung der Vergrößerung der (positiven) Größe ![]() zu
demonstrieren, kann man von einem Gleichungssystem (4.25) ausgehen,
wobei angenommen wird, daß das verwendete Modell nur 2 Parameter enthält:
zu
demonstrieren, kann man von einem Gleichungssystem (4.25) ausgehen,
wobei angenommen wird, daß das verwendete Modell nur 2 Parameter enthält:
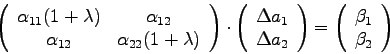

Man kann also zusammenfassen:
Eine praktikable Methode, ![]() möglichst klein (um eine möglichst
große Konvergenzgeschwindigkeit zu haben) und im Bedarfsfall doch groß
genug zu halten (um die Konvergenz zu sichern), ist die sogenannte
Marquardt'sche Strategie:
möglichst klein (um eine möglichst
große Konvergenzgeschwindigkeit zu haben) und im Bedarfsfall doch groß
genug zu halten (um die Konvergenz zu sichern), ist die sogenannte
Marquardt'sche Strategie:
Testet man den GN-Algorithmus mit Marquardt-Variation4.2 unter Verwendung der
Angaben des gegebenen Testproblems, so erhält man die in Abb.4.9
zusammengefaßten
Ergebnisse. Wie man sieht, konvergiert das Verfahren auch von jenen
Startpunkten ![]() und
und ![]() aus, bei welchen ohne die Marquardt-Variation eine
Divergenz zu beobachten war (vgl. Abb.4.8). Für den Startpunkt
aus, bei welchen ohne die Marquardt-Variation eine
Divergenz zu beobachten war (vgl. Abb.4.8). Für den Startpunkt ![]() ist im folgenden auch der Rechenverlauf dargestellt, wobei jedes * eine
Vergrößerung des Marquardt'schen Parameters
ist im folgenden auch der Rechenverlauf dargestellt, wobei jedes * eine
Vergrößerung des Marquardt'schen Parameters ![]() bedeutet:
bedeutet:
Startpunkt D OHNE MARQUARDT-VARIATION:
=========================================
t chisq a1 a2 a3 a4
0 .368339E+01 .900000E+01 .400000E+01 .350000E+01 .750000E+00
Exekutionsabbruch wegen Exponenten-Overflow!
Startpunkt D MIT MARQUARDT-VARIATION:
========================================
t chisq a1 a2 a3 a4
0 .368339E+01 .900000E+01 .400000E+01 .350000E+01 .750000E+00
*
*
*
1 .327945E+01 .116540E+02 .478102E+01 .326392E+01 .298864E+00
2 .221123E+00 .139565E+02 .407836E+01 .262388E+01 .386921E+00
3 .660544E-02 .776914E+01 .456550E+01 .253007E+01 .468859E+00
4 .383322E-04 .750890E+01 .492223E+01 .264024E+01 .496633E+00
*
5 .708586E-05 .823696E+01 .497283E+01 .278430E+01 .498760E+00
*
6 .320911E-05 .885081E+01 .498274E+01 .286453E+01 .499211E+00
7 .315072E-05 .961475E+01 .499580E+01 .296028E+01 .499807E+00
8 .101244E-06 .996144E+01 .499965E+01 .299644E+01 .499984E+00
9 .147690E-10 .999937E+01 .499999E+01 .299994E+01 .500000E+00
10 .903999E-13 .100000E+02 .500000E+01 .300000E+01 .500000E+00
11 .340838E-13 .999999E+01 .500000E+01 .300000E+01 .500000E+00
Quelle: [9], S.526f; [10], S. 683ff mit einigen Änderungen.
Das Programm MRQMIN (MaRQuardt MINimalisation) führt einen Iterationsschritt im Rahmen des Gauss-Newton-Marquardt Verfahrens durch.
INPUT-Parameter:
OUTPUT-Parameter:
Interne Felder:
Benötigte Prozeduren:
Programmstruktur:
=15cm
Struktogramm 12MRQMIN(X,Y,SIG,NDATA,MA,A,ALPHA,COVAR,
BETA,CHISQ,OCHISQ,ALAMDA,VMAR)ALAMDA ![]() 0.0ALAMDA:=0.0003MRQCOF(X,Y,SIG,NDATA,MA,A,ALPHA,BETA,CHISQ)OCHISQ:=CHISQ......I=1(1)MAJ=1(1)MANORMAL(I,J):=ALPHA(I,J)NORMAL(I,I):=ALPHA(I,I)*(1.0+ALAMDA)LUDCMP(NORMAL,MA,INDX,D,KHAD)ALAMDA
0.0ALAMDA:=0.0003MRQCOF(X,Y,SIG,NDATA,MA,A,ALPHA,BETA,CHISQ)OCHISQ:=CHISQ......I=1(1)MAJ=1(1)MANORMAL(I,J):=ALPHA(I,J)NORMAL(I,I):=ALPHA(I,I)*(1.0+ALAMDA)LUDCMP(NORMAL,MA,INDX,D,KHAD)ALAMDA ![]() 0.0J=1(1)MAI=1(1)MAVEKTOR(I):=0.0VEKTOR(J):=1.0LUBKSB(NORMAL,MA,INDX,
0.0J=1(1)MAI=1(1)MAVEKTOR(I):=0.0VEKTOR(J):=1.0LUBKSB(NORMAL,MA,INDX,
VEKTOR,LOES)I=1(1)MACOVAR(I,J):=LOES(I)LUBKSB(NORMAL,MA,INDX,BETA,DA)J=1(1)MAATRY(J):=A(J)+DA(J)MRQCOF(X,Y,SIG,NDATA,MA,ATRY,NORMAL,VEKTOR,CHISQ)CHISQ ![]() OCHISQALAMDA:=ALAMDA/5.0
OCHISQALAMDA:=ALAMDA/5.0
OCHISQ:=CHISQ
VMAR:=FALSEI=1(1)MAJ=1(1)MAALPHA(I,J):=NORMAL(I,J)BETA(I):=VEKTOR(I)
A(I):=ATRY(I)ALAMDA:=ALAMDA*5.0
VMAR:=TRUE(return)
Quelle: [9], S.527f; [10], S. 687.
Das Programm MRQCOF (MaRQuardt COeFficients) berechnet die Matrix
ALPHA und den Vektor BETA gemäß (4.20) sowie die gewichtete
Fehlerquadratsumme ![]() .
.
INPUT-Parameter:
OUTPUT-Parameter:
Benötigte Prozeduren:
=15cm
Struktogramm 13MRQCOF(X,Y,SIG,NDATA,MA,A,ALPHA,BETA,CHISQ)I=1(1)MAJ=1(1)IALPHA(I,J):=0.0BETA(I):=0.0CHISQ:=0.0K=1(1)NDATAFUNCS(X(K),A,YMOD,DYDA,MA)G:=1.0/SIG(K)/SIG(K)
DY:=Y(K)-YMODI=1(1)MAJ=1(1)IALPHA(I,J):=ALPHA(I,J) + G*DYDA(I)*DYDA(J)BETA(I):=BETA(I) + G*DY*DYDA(I)CHISQ:=CHISQ + G*DY*DYI=2(1)MAJ=1(1)I-1ALPHA(J,I):=ALPHA(I,J)(return)
=15cm
..Eingabe: 1) die NDATA Stuetzpunkte X(), Y() sowie die
Standardabweichungen SIG().
2) Anzahl MA der Modellparameter.
3) Vektor A() mit den guessed values fuer die Fit-Parameter.
4) Anzahl TMAX der maximalen Iterationsschritte.
5) relative Genauigkeit EPS der zu fittenden Parameter.T:=1
ALAMDA:=-1.0J=1(1)MAAALT(J):=A(J)MRQMIN(X,Y,SIG,NDATA,MA,A,ALPHA,COVAR,BETA,CHISQ,OCHISQ,ALAMDA,VMAR)VMARprint '***' fuer
Marquardt-Korrekturprint: T,CHISQ,A(...)DELMAX:=0.0J=1(1)MADEL:=![]() (A(J)-AALT(J))/A(J)
(A(J)-AALT(J))/A(J)![]() DEL
DEL ![]() DELMAXDELMAX:=DEL......DELMAX
DELMAXDELMAX:=DEL......DELMAX ![]() EPSALAMDA:=0.0MRQMIN(Parameter s.o.)1) Berechnung der Varianz.
EPSALAMDA:=0.0MRQMIN(Parameter s.o.)1) Berechnung der Varianz.
2) Ber. der SD der Parameter.
3) Normierung der Kovar.matrix.
4) Ausgabe: ...
(Ende der Rechnung)J=1(1)MAAALT(J):=A(J)T:=T+1T ![]() TMAXFehler: 'Genauigkeit nicht erreicht'(Ende der Rechnung)
TMAXFehler: 'Genauigkeit nicht erreicht'(Ende der Rechnung)
Gegeben sei ein radioaktives Präparat, das aus einem Gemisch von ![]() radioaktiven Isotopen besteht. Beide Kernarten zerfallen, ausgehend von
einer Anfangsaktivität
radioaktiven Isotopen besteht. Beide Kernarten zerfallen, ausgehend von
einer Anfangsaktivität ![]() mit einer Halbwertzeit
mit einer Halbwertzeit ![]() , gemäß
dem radioaktiven Zerfallsgesetz:
, gemäß
dem radioaktiven Zerfallsgesetz:
Die Gesamtaktivität der Quelle beträgt demnach
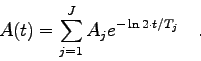
Die Messung geht nun wie folgt vor sich: Während einer fixen Zeitspanne
![]() werden die von der Quelle herrührenden Zerfälle gezählt und
das Ergebnis wird gespeichert. Danach wird die Zählung für eine zweite
Zeitspanne
werden die von der Quelle herrührenden Zerfälle gezählt und
das Ergebnis wird gespeichert. Danach wird die Zählung für eine zweite
Zeitspanne ![]() durchgeführt usw. Man erhält auf diese Weise eine
Reihe von Zählwerten
durchgeführt usw. Man erhält auf diese Weise eine
Reihe von Zählwerten ![]() , wobei
, wobei
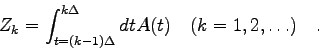
Ein solches Experiment ist natürlich ein typisches Zählexperiment d.h. die Meßwerte sind um ihre jeweiligen Erwartungswerte poisson-verteilt (s. Abschnitt 4.3.3).
Durch die Auswertung des obigen Integrals erhält man die Modellfunktion
mit ![]() Parametern
Parametern
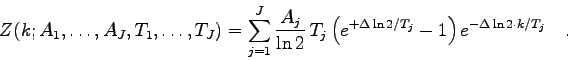
Die Ableitungen
![]() bzw.
bzw.
![]() können daraus ohne Probleme berechnet werden, und die Prozedur FUNCS
lautet in C-Version etwa folgendermaßen:
können daraus ohne Probleme berechnet werden, und die Prozedur FUNCS
lautet in C-Version etwa folgendermaßen:
#define DELTA 15.0 // Konstante des Experiments
void funcs(double x, double a[], double *z, double dzda[], int ma)
// C-VERSION
{
int mterm,j,ind;
double con,fac1,fac2,fac3,fac4;
con=DELTA*log(2.0);
mterm=ma/2;
*z=0.0;
for(j=1;j<=mterm;j++) {
ind=mterm+j;
fac1=con/a[ind];
fac2=exp(fac1);
fac3=fac2-1.0;
fac4=exp(-fac1*x);
dzda[j]=a[ind]*fac3*fac4/log(2.0);
*z=*z + a[j]*dzda[j];
dzda[ind]=a[j]/log(2.0)*fac4*(fac3*(1.0+fac1*x)-fac1*fac2);
}
}
Wie Sie sehen, wird die Routine funcs für jeden ![]() -Wert gesondert
aufgerufen. Eine solche Vorgangsweise ist im Falle einer MATLAB-Realisierung
nicht optimal, weil die Fähigkeit dieser Sprache, sehr effektiv mit Vektoren
umzugehen, nicht ausgenutzt wird. Besser ist es, wie im folgenden Beispiel
dargestellt, die Eingabegröße
-Wert gesondert
aufgerufen. Eine solche Vorgangsweise ist im Falle einer MATLAB-Realisierung
nicht optimal, weil die Fähigkeit dieser Sprache, sehr effektiv mit Vektoren
umzugehen, nicht ausgenutzt wird. Besser ist es, wie im folgenden Beispiel
dargestellt, die Eingabegröße ![]() von vornherein als Vektor
aller Werte
von vornherein als Vektor
aller Werte ![]() mit
mit
![]() vorzusehen:
vorzusehen:
function [z,dzda] = funcs(x,a,ma,ndata);
% MATLAB-VERSION x ist ein Vektor mit ndata Komponenten
dzda=zeros(ma,ndata);
delta=15.0; % Messzeit
con=delta*log(2);
mterm=fix(ma/2);
z=zeros(1,ndata);
for j=1:mterm
fac1=con/a(mterm+j);
fac2=exp(fac1);
fac3=fac2-1;
fac4=exp(-fac1*x);
dzda(j,:)=a(mterm+j)*fac3.*fac4/log(2);
z=z+a(j)*dzda(j,:);
dzda(mterm+j,:)=a(j)/log(2).*fac4.*(fac3*(1+fac1*x)-fac1*fac2);
end
Nun die Angaben zu einem konkreten Beispiel:
Gemessen wurden die Zählraten eines aus zwei Komponenten bestehenden
radioaktiven Präparates d.h. ![]() .
Es wurden 40 Messungen durchgeführt, jede über einen Zeitraum von
.
Es wurden 40 Messungen durchgeführt, jede über einen Zeitraum von
![]() Sekunden.
Sekunden.
40 Datenwerte: 1 15376.0 21 981.0 2 10903.0 22 939.0 3 7950.0 23 857.0 4 5865.0 24 790.0 5 4653.0 25 814.0 6 3721.0 26 766.0 7 3089.0 27 691.0 8 2683.0 28 681.0 9 2396.0 29 614.0 10 1992.0 30 576.0 11 1910.0 31 529.0 12 1820.0 32 488.0 13 1726.0 33 472.0 14 1600.0 34 464.0 15 1495.0 35 434.0 16 1410.0 36 380.0 17 1271.0 37 382.0 18 1197.0 38 365.0 19 1106.0 39 387.0 20 1004.0 40 296.0
Der Verlauf der Iteration mittels des Gauss-Newton-Marquardt-Verfahrens ist:
t chisq A1 A2 T1 T2
0 196876.304 2000.000 500.000 30.000 200.000
1 1233.069 976.760 237.577 26.378 184.784
2 45.645 998.414 229.228 22.949 172.341
3 43.535 1005.360 226.315 23.159 173.250
4 43.535 1005.458 226.349 23.153 173.245
5 43.535 1005.457 226.348 23.153 173.246
Konvergenz wurde erreicht!
VARIANZ = 1.209 (sollte zwischen 0.764 und 1.236 liegen)
Modellparameter SD
A1 1005.457 10.182
A2 226.348 4.129
T1(s) 23.153 0.353
T2(s) 173.246 2.320
Die Korrelationsmatrix:
A1 A2 T1 T2
A1 1.0000 -0.0494 -0.4642 0.0811
A2 -0.0494 1.0000 -0.7345 -0.9370
T1 -0.4642 -0.7345 1.0000 0.6405
T2 0.0811 -0.9370 0.6405 1.0000
Zum Abschluß noch eine grafische Darstellung der gegebenen Meßpunkte und der gefitteten Modellfunktion:
![\includegraphics[scale=0.8]{num4_fig/gnm3}](img33.png)
Im folgenden wird kurz die Vorgangsweise erläutert, wie man beim Least-Squares-Prozess verfährt, wenn die Modellparameter bestimmten linearen Zwangsbedingungen (constraints) genügen müssen. Solche Nebenbedingungen kommen in der Praxis relativ häufig vor.
Angenommen, man hat eine Modellfunktion mit ![]() Parametern vorliegen.
In diesem Fall kann es maximal
Parametern vorliegen.
In diesem Fall kann es maximal ![]() Zwangsbedingungen geben. Unter der
Voraussetzung, daß diese Bedingungen linear in den
Parametern sind, können sie so geschrieben werden:
Zwangsbedingungen geben. Unter der
Voraussetzung, daß diese Bedingungen linear in den
Parametern sind, können sie so geschrieben werden:
In diesem Fall hat die Least-Squares-Grundgleichung die Form
Ein wichtiges Problem bei der Auswertung experimenteller Daten mittels
LSQ-Methoden besteht darin, daß in vielen Fällen nicht nur die
![]() -Daten mit Meßfehlern behaftet sind, sondern auch die
-Daten mit Meßfehlern behaftet sind, sondern auch die ![]() -Daten:
denken Sie etwa an die Messung irgendeiner physikalischen Größe
in Abhängigkeit von der Zeit: in solchen Fällen wird in der Regel
nicht nur die eigentliche Meßgröße, sondern auch die (auf der
Abszisse aufgetragene) Zeit statistische Fehler aufweisen.
-Daten:
denken Sie etwa an die Messung irgendeiner physikalischen Größe
in Abhängigkeit von der Zeit: in solchen Fällen wird in der Regel
nicht nur die eigentliche Meßgröße, sondern auch die (auf der
Abszisse aufgetragene) Zeit statistische Fehler aufweisen.
In derartigen Situationen verbietet sich die Anwendung von Standard-LSQ-Methoden, wie sie in den bisherigen Abschnitten dieses Kapitels verwendet wurden, und man sollte die sog. effective variance method einsetzen. Diese Methode werde ich im Rahmen dieser LV auf Basis der folgenden Publikation erläutern:
J. Orear, Am. J. Phys. 50, 912 (1982)
Wie bei vielen Themen, ist das Problem bei der Internet-Suche nicht ein zu wenig, sondern ein zu viel: eine Eingabe des Stichwortes 'Levenberg-Marquardt' in die GOOGLE-Suchmaschine gibt über 6000 Eintragungen ...
www.mathworks.com/access/helpdesk/help/toolbox/optim/optim.shtmlüber die Optimization Toolbox informieren. Durch Anklicken der Stichworte 'Gauss-Newton Method' bzw. 'Levenberg-Marquardt Method' erfahren Sie Interessantes zum diesen Themen.