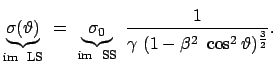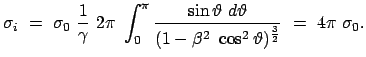Unterabschnitte
Die spezielle Relativitätstheorie beruht auf zwei Grundannahmen (= Prinzipien), dem
1. Relativitätsprinzip, und dem
2. Prinzip von der Konstanz der Vakuumlichtgeschwindigkeit c.
Beide Annahmen werden durch experimentelle Befunde nahegelegt. Doch geht auch eine
gewisse philosophische Grundeinstellung darin ein.
Wiederholung der Definition eines Inertialsystems aus §8.1:
In einem solchen System gehorcht ein Massenpunkt dem I. Newtonschen Axiom:
''Ein Massenpunkt bleibt in Ruhe oder in gleichförmiger Bewegung,
wenn keine Kraft auf ihn einwirkt.''
Ein solches System ist realisiert in einem Bezugssystem, das sich
relativ zum Fixsternhimmel in Ruhe oder in gleichförmiger Bewegung befindet.
Das Einsteinsche Relativitätsprinzip besagt, daß alle
physikalischen Vorgänge in allen Inertialsystemen bei sonst gleichen
Bedingungen gleich ablaufen. Es ist durch kein Experiment möglich,
eine absolute Geschwindigkeit eines Systems festzustellen.
Daher muß auch die mathematische Beschreibung aller physikalischen
Vorgänge in allen Inertialsystemen gleichartig sein (Kovarianz).
Ein Spezialfall dieses Einsteinschen Relativitätsprinzips ist das
Galileische Relativitätsprinzip, das nur für die klassische Mechanik
(Mechanik für Teilchengeschwindigkeiten  ) gilt: Man kann aufgrund
mechanischer Experimente keine Aussagen über den Bewegungszustand eines
gleichförmig bewegten Systems, in dem man sich befindet, machen.
) gilt: Man kann aufgrund
mechanischer Experimente keine Aussagen über den Bewegungszustand eines
gleichförmig bewegten Systems, in dem man sich befindet, machen.
Dies sind Transformationsgleichungen zwischen zwei gleichförmig bewegten
Systemen: Der Ursprung  des Systems
des Systems  (das ''bewegte'' System:
Koordinaten
(das ''bewegte'' System:
Koordinaten 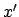 ,
, 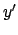 ,
, 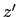 , Zeit
, Zeit 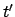 ) bewegt sich relativ zum System
) bewegt sich relativ zum System  (das ''ruhende'' System,
(das ''ruhende'' System, 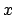 ,
, 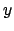 ,
, 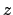 , Ursprung 0, Zeit
, Ursprung 0, Zeit
 ),s. Abb. 10.1, mit der Geschwindigkeit
),s. Abb. 10.1, mit der Geschwindigkeit 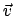 :
:
Abbildung:
Ruhendes und bewegtes System; für beide gibt es eine gemeinsame Uhr,
Gl. (10.2).
|
![\includegraphics[scale=0.9]{k10_bezugssys_uhr}](img2386.gif) |
Die vorletzte Gleichung beschreibt die absolute Zeit, unabhängig vom
Bewegungszustand des Systems. (Eine einzige Uhr, die von allen Punkten
aller Systeme aus abgelesen wird.)
In der Mechanik gibt es nur Kräfte, die zwischen Teilchen wirken und
nur von deren gegenseitiger Lage abhängen. Weiters wirken sie in der
Verbindungsgeraden der Teilchen.
Bewegungsvorgang von  aus betrachtet:
aus betrachtet:
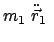 |
 |
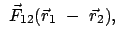 |
(104) |
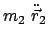 |
 |
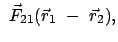 |
(105) |
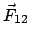 |
 |
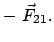 actio = reactio. actio = reactio. |
(106) |
Derselbe Vorgang vom System  aus betrachtet:
aus betrachtet:
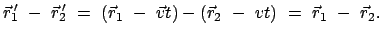 |
(107) |
Daraus folgt: Die Kräfte sind in beiden Systemen gleich, weil sie nur
vom relativen Abstand abhängen und dieser in beiden Systemen gleich ist.
Aus den Transformationsgleichungen (10.3) und (10.2) folgt:
da
 const. für gleichförmige Bewegung. Damit ergibt sich für
die Bewegungsgleichungen im System
const. für gleichförmige Bewegung. Damit ergibt sich für
die Bewegungsgleichungen im System  :
:
Die Maxwellschen Gleichungen der Elektrodynamik sind nicht invariant
gegenüber den Galileitransformationen (10.1) - (10.3).
Eine Reihe von Experimenten hat aber gezeigt, daß elektromagnetische Vorgänge
in beiden Systemen,  und
und  , genau wie die mechanischen Vorgänge in
gleicher Weise ablaufen. Um das Relativitätsprinzip zu erfüllen, muß man
die Transformationsgleichungen (10.1) - (10.3) modifizieren;
dies gibt die Lorentztransformationen.
, genau wie die mechanischen Vorgänge in
gleicher Weise ablaufen. Um das Relativitätsprinzip zu erfüllen, muß man
die Transformationsgleichungen (10.1) - (10.3) modifizieren;
dies gibt die Lorentztransformationen.
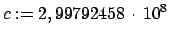
m/s .
Gemäß diesem Prinzip ist die Vakuumlichtgeschwindigkeit 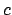 sowohl vom
Bewegungszustand des Beobachters als auch von dem der Lichtquelle völlig
unabhängig (bei alleiniger Betrachtung von Inertialsystemen). In jedem
Inertialsystem findet man, z.B., für die Ausbreitung der Wellenfront
eines Lichtblitzes den Wert
sowohl vom
Bewegungszustand des Beobachters als auch von dem der Lichtquelle völlig
unabhängig (bei alleiniger Betrachtung von Inertialsystemen). In jedem
Inertialsystem findet man, z.B., für die Ausbreitung der Wellenfront
eines Lichtblitzes den Wert 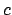 , selbst wenn die Quelle relativ zu
diesem System in gleichförmiger Bewegung ist. Bei der Schaffung der
Elektrodynamik zu Ende des vergangenen Jahrhunderts hielt man für
die Ausbreitung der elektromgnetischen Wellen ein Medium
(den sogenannten Äther) für nötig analog wie die Luft
(oder einen anderen elastisch deformierbaren Körper) für die
Ausbreitung von Schallwellen.
, selbst wenn die Quelle relativ zu
diesem System in gleichförmiger Bewegung ist. Bei der Schaffung der
Elektrodynamik zu Ende des vergangenen Jahrhunderts hielt man für
die Ausbreitung der elektromgnetischen Wellen ein Medium
(den sogenannten Äther) für nötig analog wie die Luft
(oder einen anderen elastisch deformierbaren Körper) für die
Ausbreitung von Schallwellen.
Außerdem glaubte man (irrigerweise), daß ds Relativitätsprinzip
notwendigerweise die Galileitransformation (10.1) - (10.3)
nach sich zieht. Daraus schloß man (irrigerweise), daß die
Elektrodynamik das Relativitätsprinzip nicht erfüllt und daß
es ein ausgezeichnetes Koordinatensystem gibt, das im ''"Ather'' ruht.
Man versuchte nun einen ''"Atherwind'' festzustellen, der dadurch
entstehen sollte, daß sich die Erde bei ihrer Revolution um die
Sonne relativ zum Äther bewegt.
Die Messung der Schallgeschwindigkeit kann im Prinzip auf einer Meßstrecke
erfolgen mit Nachrichtenübermittlung mittels elektrischer oder optischer
Signale (deren Geschwindigkeit (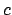 ) groß gegenüber der zu messenden
Schallgeschwindigkeit ist) vom Anfang zum Ende der Strecke (Messung der
''Einweggeschwindigkeit''). Ein derartiges Vorgehen ist bei der Messung
der Vakuumlichtgeschwindigkeit
) groß gegenüber der zu messenden
Schallgeschwindigkeit ist) vom Anfang zum Ende der Strecke (Messung der
''Einweggeschwindigkeit''). Ein derartiges Vorgehen ist bei der Messung
der Vakuumlichtgeschwindigkeit 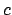 nicht möglich, da man keine Art von
Signalen kennt, deren Ausbreitungsgeschwindigkeit groß gegen
nicht möglich, da man keine Art von
Signalen kennt, deren Ausbreitungsgeschwindigkeit groß gegen 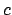 ist.
Man ist daher gezwungen, das Lichtsignal, dessen Ausbreitungsgeschwindigkeit
gemessen werden soll, am Ende der Messtrecke zu reflektieren und kann
daher nur die Laufzeit für Hin- und Rückweg messen (''Zweiweggeschwindigkeit'').
Das wichtigste der diesbezüglichen Experimente war der Michelsonversuch:
(Im Äther ist die Lichtgeschwindigkeit gemäß der damaligen Ansicht
ist.
Man ist daher gezwungen, das Lichtsignal, dessen Ausbreitungsgeschwindigkeit
gemessen werden soll, am Ende der Messtrecke zu reflektieren und kann
daher nur die Laufzeit für Hin- und Rückweg messen (''Zweiweggeschwindigkeit'').
Das wichtigste der diesbezüglichen Experimente war der Michelsonversuch:
(Im Äther ist die Lichtgeschwindigkeit gemäß der damaligen Ansicht 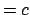 ,
für andere Systeme muß man gemäß (10.3) umrechnen, (Abb. 10.2(a)).
Der gesamte Meßapparat bewegt
,
für andere Systeme muß man gemäß (10.3) umrechnen, (Abb. 10.2(a)).
Der gesamte Meßapparat bewegt
sich relativ zum Äther mit der Geschwindigkeit 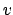 . Ein Beobachter im mitbewegten
System
. Ein Beobachter im mitbewegten
System  stellt folgende Laufzeit
stellt folgende Laufzeit 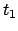 für den Weg PS
für den Weg PS P fest (P =
Position des halbdurchlässigen Spiegels):
P fest (P =
Position des halbdurchlässigen Spiegels):
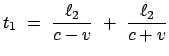 |
(1012) |
Ebenso ergibt sich im mitbewegten System aus
folgende Zeit 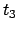 für den Lauf PS
für den Lauf PS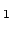 P (Abb. 10.2(b)):
Aus den beiden Laufzeiten
P (Abb. 10.2(b)):
Aus den beiden Laufzeiten
mit
 |
(1013) |
ergibt sich folgender Zeit- und damit auch Phasenunterschied
im Beobachtungsfernrohr:
Ist der Apparat um 90^&cir#circ; verdreht, ergeben sich folgende
Änderungen und folgender Laufzeit- und Phasenunterschied:
Wird nun das Interferometer während des Beobachtugsvorganges
gedreht, sollte dadurch folgender Laufzeit- und damit auch
Phasenunterschied resultieren:
Der unerwartete Nulleffekt konnte nur durch eine zusätzliche Hypothese
(Fizgerald, Lorentz) erklärt werden: Bei Bewegung relativ zu Äther
verkürzen sich Längen in der Bewegungsrichtung um den Faktor
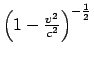 ; Längen in den
transversalen Richtungen bleiben unverändert. Dann erhält man in den obigen
Gleichungen für
Damit sind aber noch nicht alle Schwierigkeiten beseitigt;
um den negativen Ausgang weiterer Experimente deuten zu können,
waren noch zusätzliche Hypothesen über die Zeitdilatation
und die Veränderung der Kräfte bei Bewegung relativ zum
Äther erforderlich. Der Äther wird damit unbeobachtbar.
Einstein vereinfachte 1905 die Situation in radikaler und
revolutionärer Weise, indem er den Äther für die Lichtausbreitung
für unnötig erklärte und die Gültigkeit des Relativitätsprinzips
für alle physikalischen Vorgänge forderte. Weiters postulierte er,
daß die Vakuumlichtgeschwindigkeit in allen Inertialsystemen den Wert
; Längen in den
transversalen Richtungen bleiben unverändert. Dann erhält man in den obigen
Gleichungen für
Damit sind aber noch nicht alle Schwierigkeiten beseitigt;
um den negativen Ausgang weiterer Experimente deuten zu können,
waren noch zusätzliche Hypothesen über die Zeitdilatation
und die Veränderung der Kräfte bei Bewegung relativ zum
Äther erforderlich. Der Äther wird damit unbeobachtbar.
Einstein vereinfachte 1905 die Situation in radikaler und
revolutionärer Weise, indem er den Äther für die Lichtausbreitung
für unnötig erklärte und die Gültigkeit des Relativitätsprinzips
für alle physikalischen Vorgänge forderte. Weiters postulierte er,
daß die Vakuumlichtgeschwindigkeit in allen Inertialsystemen den Wert
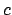 hat. Er analysierte den Begriff der Gleichzeitigkeit und zeigte,
daß jedes Inertialsystem seine eigene Zeit hat und daß Zeitangaben
von einem System ins andere mittels der Lorentztransformation
durchgeführt werden müssen.
hat. Er analysierte den Begriff der Gleichzeitigkeit und zeigte,
daß jedes Inertialsystem seine eigene Zeit hat und daß Zeitangaben
von einem System ins andere mittels der Lorentztransformation
durchgeführt werden müssen.
System  : Koordinaten
: Koordinaten
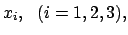 Zeit
Zeit  ;
;
System  : Koordinaten
: Koordinaten
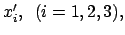 Zeit
Zeit 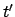 .
.
Zur Vereinfachung der Berechnung seien die beiden Koordinatensysteme
parallel und die Geschwindigkeit des Ursprungs von  liege in der
1-Achse von
liege in der
1-Achse von  :
:
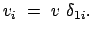 |
(1015) |
Zur Zeit
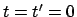 sollen die Ursprünge
sollen die Ursprünge
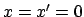 zusammenfallen und zu dieser Zeit werde ein Lichtblitz vom Ursprung
ausgesendet. Zur in
zusammenfallen und zu dieser Zeit werde ein Lichtblitz vom Ursprung
ausgesendet. Zur in  gemessenen Zeit
gemessenen Zeit  ist die Wellenfront an
ist die Wellenfront an
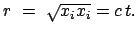 Es gilt dann:
Es gilt dann:
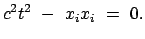 |
(1016) |
Diese Gleichung muß invarianten Charakter haben, daher gilt in
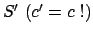 :
:
 |
(1017) |
Zur Vereinfachung der Schreibweise wird
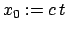 und
und
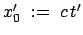 gesetzt.
Man fordert nun eine lineare Transformation:
gesetzt.
Man fordert nun eine lineare Transformation:
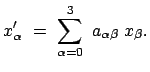 |
(1018) |
Für die Linearität einer Transformation zwischen  und
und  sprechen folgende Tatsachen:
sprechen folgende Tatsachen:
- Die Homogenität und Isotropie des freien Raumes.
- Die Bewegung eines kräftefreien Teilchens relativ
zu einem Inertialsystem wird durch eine lineare Gleichung
in den
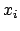 beschrieben. Dies muß für jedes Inertialsystem
gelten. Die obige Transformation aus einem Inertialsystem in ein
anderes muß daher eine lineare Gleichung wieder affin in eine solche transformieren.
beschrieben. Dies muß für jedes Inertialsystem
gelten. Die obige Transformation aus einem Inertialsystem in ein
anderes muß daher eine lineare Gleichung wieder affin in eine solche transformieren.
Bei unserer Wahl der Bewegungsrichtung gilt:
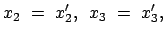 |
(1019) |
d.h. wir können von den Koordinaten 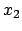 und
und 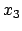 völlig absehen und
die weiteren Überlegungen in der 0,1-Ebene durchführen:
völlig absehen und
die weiteren Überlegungen in der 0,1-Ebene durchführen:
Setzt man diese Gln. in die aus Gln. (10.16) und (10.17) sich
ergebende Bedingung ein, so folgt:
Die erste Gleichung der letzten Zeile wird durch den nachfolgenden Ansatz befriedigt:
aus der zweiten folgt:
daraus wegen der dritten:
Es wird 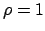 gewählt. Denn für
gewählt. Denn für 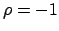 erhielte man aus
(10.20) und (10.21) eine Transformationsgleichung, bei
der entweder die Zeit umgekehrt und/oder das Rechtssystem im Raum in ein
Linkssystem transformiert werden würde. Es ist also:
erhielte man aus
(10.20) und (10.21) eine Transformationsgleichung, bei
der entweder die Zeit umgekehrt und/oder das Rechtssystem im Raum in ein
Linkssystem transformiert werden würde. Es ist also:
Der Ursprung von  ' bewegt sich mit der Geschwindigkeit
' bewegt sich mit der Geschwindigkeit 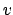 relativ zu
relativ zu  (Gl. (10.15)):
(Gl. (10.15)):
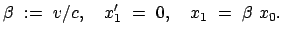 |
(1024) |
Damit folgt aus obigen Transformationsgleichungen:
und durch Umrechnung:
Damit haben wir die Lorentztransformation für eine Bewegung längs
der 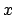 -Achse mit der Geschwindigkeit
-Achse mit der Geschwindigkeit
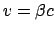 abgeleitet:
abgeleitet:
![\begin{displaymath}\begin{array}{cclcccclc} x'_0 &=& \qquad \gamma x_0 & - \...
...3, &&& x'_3 & = & x_3 . & \mbox{(d)} [1mm] \end{array}\end{displaymath}](img2475.gif) |
(1025) |
Die inversen Transformationen erhält man durch Auflösung des obigen
Gleichungssystems, einfacher noch durch Anwendung des Relativitätsprinzips
(Wechsel des Systems ist gleichbedeutend mit Umkehr der Geschwindigkeit):
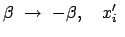 |
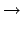 |
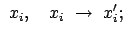 |
|
 |
 |
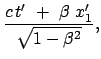 |
(1026) |
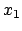 |
 |
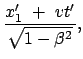 |
(1027) |
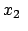 |
 |
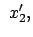 |
(1028) |
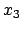 |
 |
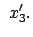 |
(1029) |
Diese Lorentztransformationen bilden eine Gruppe. Alle physikalischen Größen
transformieren sich gemäß diesen Transformationsgleichungen.
Das augenscheinlichste Ergebnis dieser neuen Transformationsgleichungen ist,
daß die Zeit keine Invariante mehr ist.
Als Grenzfall für 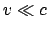 und
und
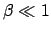 enthalten obige Gleichungen die
Galileitransformationen, Gln. (10.1) - (10.3).
enthalten obige Gleichungen die
Galileitransformationen, Gln. (10.1) - (10.3).
Für einen Beobachter B in  ist
ist  das ''Ruhesystem'' und
das ''Ruhesystem'' und  das ''bewegte System'';
für einen Beobachter B
das ''bewegte System'';
für einen Beobachter B in
in  verhält es sich gerade umgekehrt. Wir nehmen von den
obigen Lorentztransformationen nur die Gleichung für die zur Systembewegung parallele
Komponente und die Zeit.
verhält es sich gerade umgekehrt. Wir nehmen von den
obigen Lorentztransformationen nur die Gleichung für die zur Systembewegung parallele
Komponente und die Zeit.
 |
 |
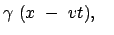 (a) (a)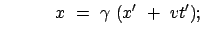 (b) (b) |
(1030) |
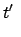 |
 |
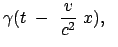 (a) (a)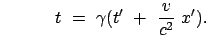 (b) (b) |
(1031) |
In jedem System werden alle Uhren untereinander synchronisiert. Z.B. wird zur
Zeit
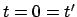 vom Ursprung
vom Ursprung
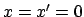 ein Lichtblitz ausgesendet.
In jedem System befindet sich bei jeder Uhr ein Spiegel,
der den Lichtblitz zum Ursprung reflektiert. Die Hälfte der ganzen Laufzeit ist
dann die Zeit, die die Uhr in dem Moment anzeigen muß,
als bei ihr der Lichtblitz eingetroffen ist.
ein Lichtblitz ausgesendet.
In jedem System befindet sich bei jeder Uhr ein Spiegel,
der den Lichtblitz zum Ursprung reflektiert. Die Hälfte der ganzen Laufzeit ist
dann die Zeit, die die Uhr in dem Moment anzeigen muß,
als bei ihr der Lichtblitz eingetroffen ist.
B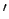 stellt fest, daß zwei Ereignisse an verschiedenen Orten seines Systems
gleichzeitig eingetreten sind:
stellt fest, daß zwei Ereignisse an verschiedenen Orten seines Systems
gleichzeitig eingetreten sind:
Z.B. sind die Ereignisse das Aufblitzen von Lichtern und diese Lichtblitze
treffen bei dem in  befindlichen Beobachter B' gleichzeitig ein.
Gemäß Gln. (10.30b) und (10.31b) gilt dann für den
Beobachter B in
befindlichen Beobachter B' gleichzeitig ein.
Gemäß Gln. (10.30b) und (10.31b) gilt dann für den
Beobachter B in  :
:
Dem Beobachter B erscheinen die beiden Ereignisse also nicht gleichzeitig.
Wenn, umgekehrt, B zwei Ereignisse an verschiedenen Orten gleichzeitig
erscheinen, so sind diese für B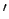 nicht gleichzeitig.
Die Gleichzeitigkeit ist also ein Begriff, der jeweils nur
in einem System Sinn hat, also keine Invariante der Transformationsgruppe ist.
nicht gleichzeitig.
Die Gleichzeitigkeit ist also ein Begriff, der jeweils nur
in einem System Sinn hat, also keine Invariante der Transformationsgruppe ist.
Wir betrachten zwei Ereignisse, die im Ursprung von
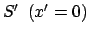 zu den Zeiten
zu den Zeiten 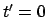 und
und
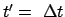 stattfinden (etwa Ablesen einer Uhr, die sich im Ursprung befindet).
stattfinden (etwa Ablesen einer Uhr, die sich im Ursprung befindet).
Daß B für die beiden Ereignisse verschiedene Ortskoordinaten mißt,
ist aufgrund des Bewegungszustandes von  leicht einsichtig. Daß B
jedoch für den Zeitunterschied die von
leicht einsichtig. Daß B
jedoch für den Zeitunterschied die von
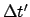 verschiedene
Zeitspanne
verschiedene
Zeitspanne
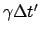 mißt, ist ein vom klassischen Standpunkt
abweichendes Resultat. Da
mißt, ist ein vom klassischen Standpunkt
abweichendes Resultat. Da
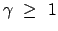 ist,
ist
ist,
ist
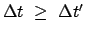 . Man sagt daher auch:
''Bewegte Uhren gehen langsamer''. Genau dasselbe stellt
B' für eine in
. Man sagt daher auch:
''Bewegte Uhren gehen langsamer''. Genau dasselbe stellt
B' für eine in  ruhende Uhr fest; sie ist für B
ruhende Uhr fest; sie ist für B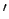 eine bewegte Uhr und scheint ihm langsamer zu gehen. Wir schreiben dies in
der folgenden Form, weisen aber darauf hin, daß diese Gleichung mit grosser
Vorsicht anzuwenden ist; eigentlich sollte man für Zeitumrechnungen immer
Gleichung wie in den Lorentztransformationen benutzen.
eine bewegte Uhr und scheint ihm langsamer zu gehen. Wir schreiben dies in
der folgenden Form, weisen aber darauf hin, daß diese Gleichung mit grosser
Vorsicht anzuwenden ist; eigentlich sollte man für Zeitumrechnungen immer
Gleichung wie in den Lorentztransformationen benutzen.
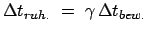 |
(1032) |
Operationelle Beobachtung der Zeitdilatation
Beobachter B hat in seinem System längs der 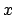 -Achse an allen Orten
Uhren aufgestellt und synchronisiert (in seinem System ist ja der
Begriff der Gleichzeitigkeit sinnvoll). Die Uhren des Systems
-Achse an allen Orten
Uhren aufgestellt und synchronisiert (in seinem System ist ja der
Begriff der Gleichzeitigkeit sinnvoll). Die Uhren des Systems  (dort ruhend) fliegen an denen des Systems
(dort ruhend) fliegen an denen des Systems  vorbei und werden mit den
jeweils gegenüberliegenden Uhren von
vorbei und werden mit den
jeweils gegenüberliegenden Uhren von  verglichen.
Dies ergibt zu den Zeitpunkten
verglichen.
Dies ergibt zu den Zeitpunkten 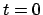 bzw.
bzw.
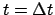 :
Für einen Uhrenvergleich zum Nachweis der Zeitdilatation benötigt
man mindestens 3 Uhren (z.B. in
:
Für einen Uhrenvergleich zum Nachweis der Zeitdilatation benötigt
man mindestens 3 Uhren (z.B. in  in
in 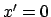 ; in
; in  in
in
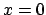 und
und 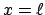 ).
).
Abbildung 10.3:
Zeitanzeigen der Uhren in verschiedenen bewegten Systemen
|
![\includegraphics[scale=0.83]{k10_zeitanzeige_t0}](img2521.gif)
![\includegraphics[scale=0.83]{k10_zeitanzeige_t1}](img2522.gif) |
Experimenteller Nachweis der Zeitdilatation an Myonen:
Myonen entstehen beim radioaktiven Zerfall des Pions (Pi-Mesons).
Das Myon könnte als ein schweres Elektron bezeichnet werden
(
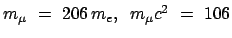 MeV);
es hat einen radioaktiven Zerfall mit einer Lebensdauer von
MeV);
es hat einen radioaktiven Zerfall mit einer Lebensdauer von 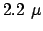 s:
s:
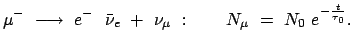 |
(1033) |
Das Pion wird mittels einer Kernreaktion erzeugt:
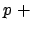 Kern Kern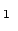 |
 |
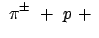 Kern Kern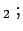 |
|
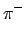 |
 |
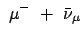 (radioaktiver Zerfall) (radioaktiver Zerfall) |
|
Myonen werden von einfallenden Teilchen der kosmischen Höhenstrahlung
über die obige Pionenreaktion erzeugt und fliegen mit annähernd
Lichtgeschwindigkeit weiter und können daher in
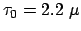 s
höchstens eine Strecke von 660 m zurücklegen. Man kann die Myonen aber noch
in Meereshöhe, also nach einem Flugweg von 6 - 10 km, nachweisen. Die aus der
Lorentztransformation folgende Zeitdilatation erklärt diese Erscheinung.
s
höchstens eine Strecke von 660 m zurücklegen. Man kann die Myonen aber noch
in Meereshöhe, also nach einem Flugweg von 6 - 10 km, nachweisen. Die aus der
Lorentztransformation folgende Zeitdilatation erklärt diese Erscheinung.
Abbildung:
Myonen in der Atmosphäre
|
![\includegraphics[scale=0.85]{k10_zeitanzeige_mueon1}](img2534.gif)
![\includegraphics[scale=0.85]{k10_zeitanzeige_mueon2}](img2535.gif) |
Wenn ein Myon mit
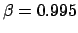 , d.h.
, d.h.
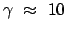 , fliegt,
dann mißt man von der Erde aus anstelle von
, fliegt,
dann mißt man von der Erde aus anstelle von
 s
die längere mittlere Lebensdauer von
s
die längere mittlere Lebensdauer von
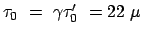 s.
Diese Zeit reicht aus, um eine Strecke von 6 km zurückzulegen.
Dieser Effekt wurde bei Beobachtungen genau untersucht. Wegen des
statistischen Charakters des Zerfallsgesetzes ist dieses Experiment
nicht so einfach durchzuführen, wie in der obigen Abbildung schematisiert.
Es wurden die Myonenzahlen in verschiedenen Höhen registriert und
daraus die Lebensdauer deduziert.(s. J. H. Smith, §3.5).
s.
Diese Zeit reicht aus, um eine Strecke von 6 km zurückzulegen.
Dieser Effekt wurde bei Beobachtungen genau untersucht. Wegen des
statistischen Charakters des Zerfallsgesetzes ist dieses Experiment
nicht so einfach durchzuführen, wie in der obigen Abbildung schematisiert.
Es wurden die Myonenzahlen in verschiedenen Höhen registriert und
daraus die Lebensdauer deduziert.(s. J. H. Smith, §3.5).
Zwei Uhren, eine fliegt im Raumschiff mit, die andere bleibt auf der Erde.
(Von der Wirkung des Gravitationsfeldes auf die Uhr, die im Rahmen der
allgemeinen Relativitätstheorie behandelt werden kann, wird abgesehen.)
Das Raumschiff beschleunigt bis nahe an 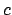 und fliegt gleichförmig bis zu einem
und fliegt gleichförmig bis zu einem
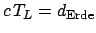 entfernten Himmelskörper, kehrt dort um
und fliegt gleichförmig wieder zurück.
entfernten Himmelskörper, kehrt dort um
und fliegt gleichförmig wieder zurück.
Abbildung 10.5:
Flug eines Raumschiffs von der Erde zur Sonne
|
![\includegraphics[scale=0.85]{k10_erde_sonne}](img2541.gif) |
Ein Beobachter, der am Startpunkt der Rakete in Ruhe zurückbleibt,
mißt die folgende Flugzeit:
bis zum Eintreffen des Raumschiffes am Zielpunkt. Ein Beobachter im fliegenden
Raumschiff liest von seiner Uhr die Zeit (= Eigenzeit)
ab. Da
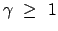 ist, scheint für ihn die Zeit langsamer vergangen
zu sein. Wenn der Raumfahrer zurückkehrt, wird er weniger gealtert sein,
als sein auf der Erde zurückgebliebener Zwillingsbruder
(von Wirkungen des Gravitationsfeldes abgesehen !).
ist, scheint für ihn die Zeit langsamer vergangen
zu sein. Wenn der Raumfahrer zurückkehrt, wird er weniger gealtert sein,
als sein auf der Erde zurückgebliebener Zwillingsbruder
(von Wirkungen des Gravitationsfeldes abgesehen !).
z.B. Erde
-Centauri
4.5 Jahre
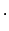
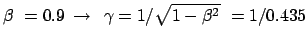 Im System des Raumfahrers zeigt die Uhr also nur etwa halb so viel Zeit, wie das Licht
zur Bewältigung dieser Strecke braucht.
Für den auf der Erde verbliebenen Zwillingsbruder vergeht also währenddessen
die 1.11-fache Zeit, die das Licht braucht, um von
Im System des Raumfahrers zeigt die Uhr also nur etwa halb so viel Zeit, wie das Licht
zur Bewältigung dieser Strecke braucht.
Für den auf der Erde verbliebenen Zwillingsbruder vergeht also währenddessen
die 1.11-fache Zeit, die das Licht braucht, um von  -Centauri zur
Erde zu gelangen.
-Centauri zur
Erde zu gelangen.
Die Anwendung der Speziellen Relativitätstheorie ist in diesem Falle eigentlich
nicht gerechtfertigt, da Beschleunigungen auftreten. Die Behandlung obigen Vorganges
nach der Allgemeinen Relativitätstheorie führt jedoch zum selben Ergebnis. (s. M. Born)
Das g-2-Experiment am Myonspeicherring bei CERN
Die Zeitdilatation kann auch beim g-2 Experiment im Myonenspeicherring
beobachtet werden. Das Myon hat ein magnetisches Moment  ;
dieses präzediert im Magnetfeld des Speicherringes
s. Abb. 10.6(a). Die Präzessionsgeschwindigkeit
gestattet es, die Größe von
;
dieses präzediert im Magnetfeld des Speicherringes
s. Abb. 10.6(a). Die Präzessionsgeschwindigkeit
gestattet es, die Größe von  und damit des magnetischen Moments zu bestimmen.
Die Präzession kann beobachtet werden, weil die Emission der Elektronen bzw. Positronen beim
Zerfall des Myons
und damit des magnetischen Moments zu bestimmen.
Die Präzession kann beobachtet werden, weil die Emission der Elektronen bzw. Positronen beim
Zerfall des Myons
eine Vorzugsrichtung in Richtung des magnetischen Momentes hat. Die emittierten
Elektronen bzw. Positronen werden mit Zählern registriert. Aus der Abnahme
der Zählrate kann die mittlere Lebensdauer der Myonen nach dem Zerfallsgesetz
(10.33) bestimmt werden, aus der 'Modulation' der e-Potenz das gesuchte g-2.
(s. Abb. 10.6(b)).
Abbildung:
a) Der Myon-Speicherring. b) Zählrate der Elektronen bzw. Positronen
|
[]
![\includegraphics[scale=0.6]{k10_myonenspeicherring}](img2551.gif) []
[]
![\includegraphics[scale=0.65]{k10_muon}](img2552.gif) |
Dieses Problem wäre streng genommen auch nicht nach der Speziellen Relativitätstheorie
lösbar. Wir setzen in der Lorentztransformation 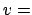 Tangentialgeschwindigkeit
der umlaufenden Myonen. Für
Tangentialgeschwindigkeit
der umlaufenden Myonen. Für
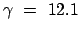 ergibt sich theoretisch eine
vom Laborsystem (der Erde) aus gemessene Lebensdauer von
ergibt sich theoretisch eine
vom Laborsystem (der Erde) aus gemessene Lebensdauer von
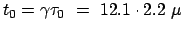 s
s
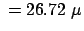 s.
Gemessen wurde ein Wert von
s.
Gemessen wurde ein Wert von
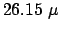 s. Kleine Diskrepanz aufgrund von Meßfehlern.
s. Kleine Diskrepanz aufgrund von Meßfehlern.
In  ruht ein Stab der Länge
ruht ein Stab der Länge 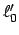 , d.h. ein Beobachter in
, d.h. ein Beobachter in  beschreibt
die Endpunkte des Stabes mit den Koordinaten:
beschreibt
die Endpunkte des Stabes mit den Koordinaten:
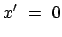
und
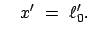
Ein Beobachter B in  mißt zur Zeit
mißt zur Zeit 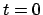 für die beiden Endpunkte die Koordinaten
für die beiden Endpunkte die Koordinaten
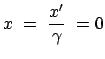
und
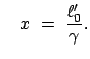
B sagt , der Maßstab habe eine Länge
 ,
sei also aufgrund der Bewegung verkürzt. Doch gibt es kaum eine Möglichkeit,
diese Lorentzkontraktion
,
sei also aufgrund der Bewegung verkürzt. Doch gibt es kaum eine Möglichkeit,
diese Lorentzkontraktion
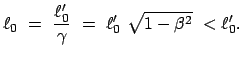 |
(1034) |
experimentell zu beobachten.
Bei ausgedehnten Körpern muß man zusätzlich beachten, daß die von
vom Beobachter weiter entfernten Punkten des Körpers ausgehenden
Lichtstrahlen erst später eintreffen als die von näher gelegenen Teilen.
Dadurch würde ein solcher Körper verzerrt bzw. verdreht erscheinen.
Ein System  bewege sich mit
bewege sich mit
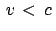 relativ zu
relativ zu  . Ein weiteres System
. Ein weiteres System 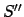 bewege sich mit
bewege sich mit
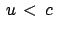 relativ zu
relativ zu  . Dann ist die Summe
. Dann ist die Summe
 . Da aber auch
. Da aber auch 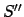 die Grenzgeschwindigkeit
die Grenzgeschwindigkeit 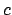 nicht
überschreiten kann, kann die obige Addition der Geschwindigkeiten nicht
richtig sein. Tatsächlich liegt ein Trugschluß vor; dieser wird nur
vermieden, wenn man bei jedem Wert der Geschwindigkeit die Zeit des
betreffenden Systems benutzt.
nicht
überschreiten kann, kann die obige Addition der Geschwindigkeiten nicht
richtig sein. Tatsächlich liegt ein Trugschluß vor; dieser wird nur
vermieden, wenn man bei jedem Wert der Geschwindigkeit die Zeit des
betreffenden Systems benutzt.
Abbildung 10.7:
Zum Additionstheorem der Geschwindigkeiten
|
![\includegraphics[scale=0.85]{k10_add_theorem}](img2569.gif) |
Beide Systeme,  und
und 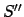 , bewegen sich in
, bewegen sich in 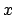 -Richtung:
-Richtung:
-
 relativ zu
relativ zu  mit Geschwindigkeit
mit Geschwindigkeit 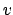 ;
;
-
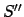 relativ zu
relativ zu  mit Geschwindigkeit
mit Geschwindigkeit
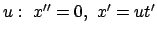 ;
;
-
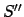 relativ zu
relativ zu  mit Geschwindigkeit
mit Geschwindigkeit 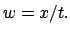
Damit lautet das Additionstheorem für die (gleichgerichteten) Geschwindigkeiten:
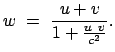 |
(1035) |
Es gilt also nicht mehr das vektorielle Addieren von Geschwindigkeiten wie in
der klassischen Mechanik. Auch folgt daraus, daß die resultierende
Geschwindigkeit immer kleiner ist als 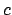 , wenn nur
, wenn nur 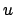 und
und 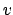 kleiner als
kleiner als
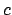 sind. (Z.B.:
sind. (Z.B.:
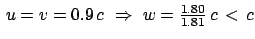 .)
.)
Eine experimentelle Überprüfung des obigen Additionstheorems ergibt sich aus
dem Fizeauschen Mitführungsversuch:
Abbildung:
Fizeauschen Mitführungsversuch.
|
![\includegraphics[scale=0.85]{k10_fizeau_mitfuehr}](img2575.gif) |
Eine Flüssigkeit mit Brechungsindex 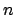 fließt mit Geschwindigkeit
fließt mit Geschwindigkeit 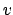 .
In der ruhenden Flüssigkeit ist die Lichtgeschwindigkeit
.
In der ruhenden Flüssigkeit ist die Lichtgeschwindigkeit 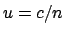 .
Die Lichtgeschwindigkeit im Labor (bei fließendem Wasser) beträgt:
.
Die Lichtgeschwindigkeit im Labor (bei fließendem Wasser) beträgt:
in Übereinstimmung mit dem Experiment.
Bisher wurde angenommen, daß die relative Geschwindigkeit der beiden Systeme S und S'
parallel zur 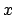 -Achse ist. Nun sei der Vektor der Geschwindigkeit von S' relativ zu S
gleich
-Achse ist. Nun sei der Vektor der Geschwindigkeit von S' relativ zu S
gleich 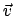 . Um die Gesetzmäßigkeit anwenden zu können, die sich in den Formeln
(10.25) zeigt, zerlegen wir den Vektor
. Um die Gesetzmäßigkeit anwenden zu können, die sich in den Formeln
(10.25) zeigt, zerlegen wir den Vektor 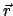 in eine Komponente parallel zu
in eine Komponente parallel zu 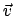 und in eine senkrecht zu
und in eine senkrecht zu 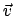 . Die senkrechte Komponente bleibt unverändert.
Für die Zeittransformation ist statt
. Die senkrechte Komponente bleibt unverändert.
Für die Zeittransformation ist statt 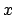 die Projektion von
die Projektion von 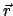 auf
auf 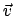 zu setzen.
zu setzen.
Abbildung:
Zur Lorentztransformation bei einer Systemgeschwindigkeiten 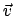 in
allgemeiner Richtung.
in
allgemeiner Richtung.
|
![\includegraphics[scale=0.85]{k10_bezugssysteme}](img2578.gif) |
Eine gleiche Zerlegung wird auch für
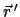 vorgenommen. Aus
Gln. (10.25) folgt sinngemäß:
In diese Formel werden die obigen Zerlegungen für
vorgenommen. Aus
Gln. (10.25) folgt sinngemäß:
In diese Formel werden die obigen Zerlegungen für 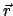 und
und 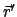 eingesetzt:
eingesetzt:
Damit ist die Lorentztransformation für die Bewegung von S relativ zu S' mit
der Geschwindigkeit 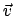 gefunden:
gefunden:
Diese Lorentztransformationen bilden keine Gruppe. Denn das
Hintereinanderausführen von Lorentztransformationen zu den Geschwindigkeiten
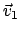 bzw.
bzw. 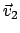 (mit
(mit
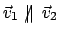 )
gibt im allgemeinen eine Transformation,
die auch eine Drehung enthält. Wenn man aber die räumliche Drehgruppe dazunimmt,
dann erhält man eine Gruppe, die Lorentzgruppe.
)
gibt im allgemeinen eine Transformation,
die auch eine Drehung enthält. Wenn man aber die räumliche Drehgruppe dazunimmt,
dann erhält man eine Gruppe, die Lorentzgruppe.
Da in der Relaltivitätstheorie die Zeit  eine system- und ortsabhängige Größe
ist, muß sie zusammen mit den Ortskoordinaten
eine system- und ortsabhängige Größe
ist, muß sie zusammen mit den Ortskoordinaten 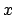 ,
, 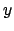 ,
, 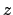 zur systembezogenen Beschreibung
eines physikalischen Ereignisses herangezogen werden. Es ist zweckmäßig,
die Zeit
zur systembezogenen Beschreibung
eines physikalischen Ereignisses herangezogen werden. Es ist zweckmäßig,
die Zeit  als 4. Komponente eines Vektors zu schreiben. Damit diese 4. Komponente
die gleiche Dimension hat wie die drei ersten Komponenten, wird der Lichtweg
als 4. Komponente eines Vektors zu schreiben. Damit diese 4. Komponente
die gleiche Dimension hat wie die drei ersten Komponenten, wird der Lichtweg
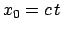 statt der reinen Zeit gewählt. Der Raum dieser
vierdimensionalen Vektoren heißt die Minkowskiwelt. Diese wird unten
in der rechten Spalte eingeführt. Zum Vergleich werden die analogen bekannten
Formeln der üblichen dreidimensionalen Vektorrechnung in der linken Spalte angegeben.
Die Minkowskiwelt ist nicht euklidisch. Deswegen gibt es hier ko- (Index unten) und
kontravariante Koordinaten (Index oben); und dies muß bei der Definition des skalaren
Produktes berücksichtigt werden.
statt der reinen Zeit gewählt. Der Raum dieser
vierdimensionalen Vektoren heißt die Minkowskiwelt. Diese wird unten
in der rechten Spalte eingeführt. Zum Vergleich werden die analogen bekannten
Formeln der üblichen dreidimensionalen Vektorrechnung in der linken Spalte angegeben.
Die Minkowskiwelt ist nicht euklidisch. Deswegen gibt es hier ko- (Index unten) und
kontravariante Koordinaten (Index oben); und dies muß bei der Definition des skalaren
Produktes berücksichtigt werden.
3-dimens. Euklidischer Raum
Koordinaten:
Vektor:
Summationsübereinkommen für wiederholte Indices von 1 bis 3.
Inneres Produkt zweier Vektoren:
Norm des Ortsvektors
|
4-dimens. Minkowskiwelt
kontravariante Koordinaten:
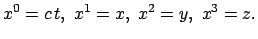 |
(1038) |
4-Vektor der Raum-Zeit:
| |
|
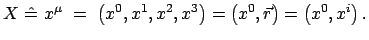 |
|
| |
|
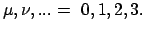 |
(1039) |
Summationsübereinkommen für wiederholte lateinische Indices von 1 bis 3;
griechische Indices von 0 bis 3.
Inneres Produkt zweier 4-Vektoren:
Norm des Raum-Zeit-Vektors:
|
Die Variable 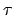 heißt die Eigenzeit; sie wird mit einer Uhr gemessen, die im Ursprung,
heißt die Eigenzeit; sie wird mit einer Uhr gemessen, die im Ursprung, 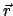 des Systems des beobachteten Teilchens ruht.
Die Definition des inneren Produkts zweier Vierervektoren gemäß (10.40) wird verständlich,
wenn man auf Gl. (10.42) schaut: Das innere Produkt zweier Vektoren muß invariant bleiben,
im dreidimensionalen Ortsraum beim Drehungen, in der Minkowskiwelt bei Drehungen im
Ortsraum, insbesondere auch bei Lorentztransformationen. Bei letzteren muß aber die Wellenfront
eines Lichtblitzes immer eine Kugel sein, d.h. es muß
des Systems des beobachteten Teilchens ruht.
Die Definition des inneren Produkts zweier Vierervektoren gemäß (10.40) wird verständlich,
wenn man auf Gl. (10.42) schaut: Das innere Produkt zweier Vektoren muß invariant bleiben,
im dreidimensionalen Ortsraum beim Drehungen, in der Minkowskiwelt bei Drehungen im
Ortsraum, insbesondere auch bei Lorentztransformationen. Bei letzteren muß aber die Wellenfront
eines Lichtblitzes immer eine Kugel sein, d.h. es muß
![$ x^2 + y^2 + z^2 - (c t)^2 = - [(c t)^2 - x^2 - y^2 - z^2]$](img2618.gif) invariant bleiben.
Das zwingt uns zu einer entsprechenden Definition des inneren Produkts wie oben in
Gl. (10.41) mittels eines ko- oder kontravarianten Maßtensors. Dieser ist hier
immer diagonal und hat konstante Elemente:
invariant bleiben.
Das zwingt uns zu einer entsprechenden Definition des inneren Produkts wie oben in
Gl. (10.41) mittels eines ko- oder kontravarianten Maßtensors. Dieser ist hier
immer diagonal und hat konstante Elemente:
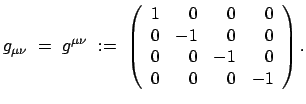 |
(1044) |
Mittels des Maßtensors kann man ko- in kontravariante Vektoren umrechnen und umgekehrt;
man kann ''Indices hinauf- und hinunterziehen'':
Es gibt auch Definitionen des Maßtensors, bei denen die Vorzeichen gerade vertauscht sind,
also ein 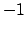 in der 1. Zeile, drei
in der 1. Zeile, drei 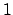 in den nachfolgenden Zeilen.
in den nachfolgenden Zeilen.
Eine andere Möglichkeit die Invarianz der kugelförmigen Wellenfront und damit der obigen
quadratischen Form einzuhalten, besteht darin, statt des reellen Lichtwegs 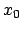 im
Raum-Zeit-Vektor eine vierte rein imaginäre Komponente einzuführen, also diesen
Vektor folgendermaßen zu definieren:
im
Raum-Zeit-Vektor eine vierte rein imaginäre Komponente einzuführen, also diesen
Vektor folgendermaßen zu definieren:
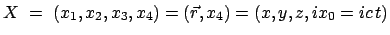
mit
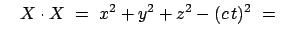
inv.
Das war die ursprüngliche Definition Minkowskis; darin erspart man sich die Unerscheidung
von ko- und kontravarianten Komponenten. Dafür muß man komplex Rechengrößen in Kauf
nehmen, während bei Benutzung der obigen Definitionen mit Maßtensoren alle Rechnungen
im Rellen bleiben. Deswegen hat sich diese durchgesetzt.
Den Koordinatentransformationen im dreidimensionalen Euklidischen Raum entsprechen
hier die Lorentztransformationen:
|
Koordinatentransformationen:
Drehung des Koordinatensystems:
|
Lorentztransformationen:
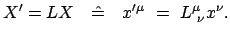 |
(1045) |
Lorentztransformation für Bewegung längs der 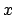 -Achse, Gl. (10.25): -Achse, Gl. (10.25):
![$\displaystyle L = \big( L^\mu_{ \nu} \big) = \left( \begin{array}{cccc...
...[2mm] 0 & 0 & 1 & 0 [2mm] - \beta\gamma & 0 & 0 & \gamma \end{array} \right)$](img2628.gif) |
(1046) |
Lorentztransformation für Vektor 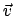 (= ''boost''),
Gln. (10.36) und (10.37): (= ''boost''),
Gln. (10.36) und (10.37):
![$\displaystyle L = \big( L^\mu_{ \nu} \big) = \left( \begin{array}{c\ve...
...j_{ 0} [1mm] \hline \vspace*{1mm} L^0_{ k} & L^j_{ k} \end{array} \right)$](img2629.gif) |
(1047) |
mit
|
Die Matrix der Lorentztransformation (10.47) ist in Kästchenform geschrieben. In der
linken oberen Ecke steht das Element 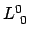 . Rechts davon stehen in der Zeile noch
3 Elemente. In der rechten unteren Ecke ist eine 3 x 3 Matrix; davor steht eine Spalte mit
3 Elementen.
. Rechts davon stehen in der Zeile noch
3 Elemente. In der rechten unteren Ecke ist eine 3 x 3 Matrix; davor steht eine Spalte mit
3 Elementen.
Der Abstand zweier Punkte, insbesondere auch die Norm des Ortsvektors 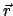 sollen
invariant sein gegenüber einer linearen Koordinatentransformation. Ebenso soll die Norm
sollen
invariant sein gegenüber einer linearen Koordinatentransformation. Ebenso soll die Norm
 des Raum-Zeit-Vektors invariant gegenüber einer Lorentztransformation sein.
des Raum-Zeit-Vektors invariant gegenüber einer Lorentztransformation sein.
Lorentztransformationen:
![\begin{displaymath}\begin{array}{rcl} L_{\nu}^{ \mu} L^{\nu}_{ \lambda} & = ...
...em] \tilde{L} L & = E = & L \tilde{L} . \end{array}\end{displaymath}](img2651.gif) |
(1048) |
|
Die 3 x 3 Matrizen 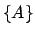 sind reell und orthogonal; sie bilden die Drehgruppe
des
sind reell und orthogonal; sie bilden die Drehgruppe
des
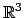 . Die Lorentztransformationen
. Die Lorentztransformationen 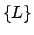 (4 x 4 Matrizen)
bilden die Lorentzgruppe.
(4 x 4 Matrizen)
bilden die Lorentzgruppe.
Summe und Differenz zweier Vektoren werden wie üblich durch die Summe bzw.
Differenz der jeweiligen Komponenten definiert. Demgemäß definiert man das
Differential des Ortsvektors bzw. des Raum-Zeit-Vektors. 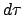 ist das
Differential der Eigenzeit, umgerechent gemäß Gl. (10.32).
ist das
Differential der Eigenzeit, umgerechent gemäß Gl. (10.32).
Relativistische Kinematik
Bei der Definition des Geschwindigkeitsvektors ist zu beachten, daß die
Ausdrücke 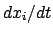 nicht ganz angepaßt sind, weil
nicht ganz angepaßt sind, weil  selbst eine
Koordinate ist. Man muß nach einem invariaten Parameter ableiten.
Dafür wird die Eigenzeit
selbst eine
Koordinate ist. Man muß nach einem invariaten Parameter ableiten.
Dafür wird die Eigenzeit 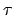 verwendet.
Man betrachtet den Raum-Zeit-Vektor
verwendet.
Man betrachtet den Raum-Zeit-Vektor 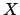 als Funktion von
als Funktion von 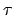 und
bildet die Ableitung nach
und
bildet die Ableitung nach 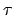 , dies gibt die
Vierergeschwindigkeit U. Die Ableitungen nach
, dies gibt die
Vierergeschwindigkeit U. Die Ableitungen nach 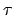 haben jedoch hauptsächlich theoretische Bedeutung, da z.B.
Messungen meist im Ruhsystem des Beobachters, also im Laborsystem,
ausgeführt werden. Man kann aber für
haben jedoch hauptsächlich theoretische Bedeutung, da z.B.
Messungen meist im Ruhsystem des Beobachters, also im Laborsystem,
ausgeführt werden. Man kann aber für 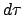 den Ausdruck
den Ausdruck 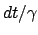 substituieren (s. Gl. (10.32)).
substituieren (s. Gl. (10.32)).
Punkte bezeichnen Ableitungen nach  . Im Eigensystem des Teilchens gilt:
. Im Eigensystem des Teilchens gilt:
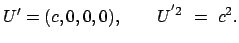 |
(1052) |
Da das skalare Produkt invariant ist, muß das letzte Resultat für jeden
Vektor der Vierergeschwindigkeit in jedem System gelten:
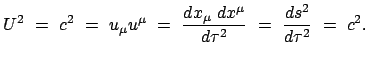 |
(1053) |
Die Vierergeschwindigkeit kann also auch in dieser Weise geschrieben werden:
Die Verallgemeinerung des 3-dimensionalen klassischen Impulses,
Gl. (3.18), in die 4-dimensionale Minkowskiwelt führt zum
Viererimpuls:
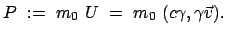 |
(1054) |
|
Die Masse 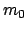 wird als die Ruhmasse (E. rest mass)
bezeichnet und ist gleich der im Eigensystem des bewegten Teilchens gemessenen Masse;
praktisch ist dies die Masse, die man bei geringer Teilchengeschwindigkeit mißt.
Die bewegte Masse ist:
wird als die Ruhmasse (E. rest mass)
bezeichnet und ist gleich der im Eigensystem des bewegten Teilchens gemessenen Masse;
praktisch ist dies die Masse, die man bei geringer Teilchengeschwindigkeit mißt.
Die bewegte Masse ist:
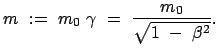 |
(1055) |
Der Raumanteil des Viererimpulses ist:
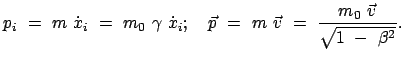 |
(1056) |
Er geht für geringe Teilchengeschwindigkeit in den gewöhnlichen klassischen
Impuls (Gl. (10.54), linke Seite) über. Die 4. Komponente des Viererimpulses ist
die Energie des Teilchens dividiert durch c. Denn nehmen wir diese
Gleichsetzung vor und entwickeln in eine binomische Reihe
so sieht man, daß der 2. Term die klassische kinetische Energie darstellt,
also müssen die anderen Terme auch Energien darstellen.
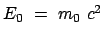 wird als die Ruhenergie (E. rest energy)
der Masse
wird als die Ruhenergie (E. rest energy)
der Masse 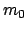 bezeichnet. Der Viererimpuls wird auch als der
Energie-Impulsvektor bezeichnet:
bezeichnet. Der Viererimpuls wird auch als der
Energie-Impulsvektor bezeichnet:
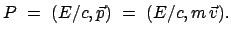 |
(1057) |
Für die Relativistische Dynamik muß eine Verallgemeinerung des zweiten
Newtonschen Axioms aufgesucht werden. Die Erfahrung widerspricht Gleichungen der Art:
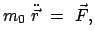
oder
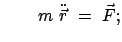
auch vertragen sich solche Gleichungen nicht mit dem Kalkül der
vierdimensionalen Minkowskiwelt. Zur Verallgemeinerung eignet
sich die Form der klassischen Bewegungsgleichung in (3.17).
Formal setzt man dann an wie in der rechten Spalte:
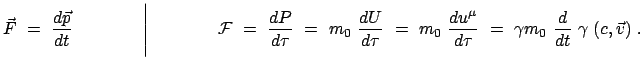 |
(1058) |
Die ersten drei Komponenten dieser Bewegungsgleichung geben im Laborsystem
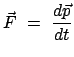 mit mit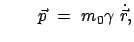 |
(1059) |
falls für die drei raumartigen Komponenten der Viererkraft gesetzt wird:
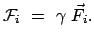 |
(1060) |
Um eine Aussage über die nullte (die zeitartige) Komponente der Viererkraft,
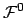 , machen zu können, wird zuerst eine Hilfsrelation abgeleitet.
Dazu werden die Vierergeschwindigkeit und die Viererkraft znächst im Ruhesystem
angesetzt. Es zeigt sich, daß ihr skalares Produkt Null ist. Da dieses eine
Lorentzinvariante ist, ist das Produkt in jedem System Null. Daraus kann man
eine Formel für
, machen zu können, wird zuerst eine Hilfsrelation abgeleitet.
Dazu werden die Vierergeschwindigkeit und die Viererkraft znächst im Ruhesystem
angesetzt. Es zeigt sich, daß ihr skalares Produkt Null ist. Da dieses eine
Lorentzinvariante ist, ist das Produkt in jedem System Null. Daraus kann man
eine Formel für
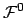 ableiten:
ableiten:
| |
|
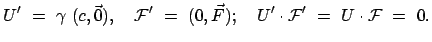 |
|
| |
|
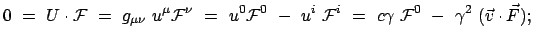 |
(1061) |
mit 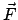 der Kraft auf das Teilchen. Daraus ergibt sich für die nullte Komponente der
Viererkraft:
der Kraft auf das Teilchen. Daraus ergibt sich für die nullte Komponente der
Viererkraft:
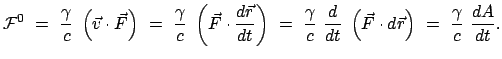 |
(1062) |
Für eine nicht zeitabhängige Kraft ist die nullte Komponente der Viererkraft proportional
zur Leistung.
Für die Beschleunigung auf relativistische Geschwindigkeiten kommen fast nur
Elementarteilchen oder Ionen in Frage. Für die Bewegung eines geladenen Teilchens in
einem elektromagnetischen Feld besteht die Kraft aus zwei Anteilen:
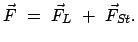 |
(1063) |
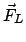 ist die Lorentzkraft:
ist die Lorentzkraft:
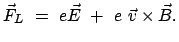 |
(1064) |
Die Strahlungsrückwirkungskraft
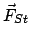 entsteht dadurch, daß jede
beschleunigte Ladung ein elektromagnetisches Feld (elm. Wellen) abstrahlt.
Dieses Feld wirkt auf die Ladung zurück. Diese Strahlungsrückwirkungskraft
ist sehr kompliziert zu berechnen. Da sie oft klein ist, wird sie meist
in einem ersten Näherungsschritt weggelassen und
erst in einem weiteren berücksichtigt, nachdem die Bewegungsgleichungen
ohne diese gelöst worden sind. Unter dieser Vernachlässigung
lautet dann die Bewegungsgleichung im Laborsystem:
entsteht dadurch, daß jede
beschleunigte Ladung ein elektromagnetisches Feld (elm. Wellen) abstrahlt.
Dieses Feld wirkt auf die Ladung zurück. Diese Strahlungsrückwirkungskraft
ist sehr kompliziert zu berechnen. Da sie oft klein ist, wird sie meist
in einem ersten Näherungsschritt weggelassen und
erst in einem weiteren berücksichtigt, nachdem die Bewegungsgleichungen
ohne diese gelöst worden sind. Unter dieser Vernachlässigung
lautet dann die Bewegungsgleichung im Laborsystem:
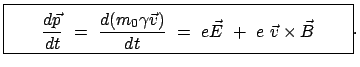 |
(1065) |
Für eine zeitunabhängige Kraft 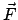 , die ein Potential
, die ein Potential 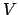 besitzt:
besitzt:
gilt also:
Das ist die Gesamtenergie:
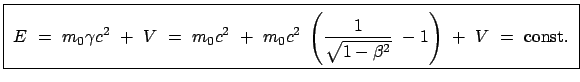 |
(1066) |
Gesamtenergie = Ruhenergie + kinetische Energie + potentielle Energie.
Die Anfangsbedingungen werden in Richtung des elektrischen Feldes gewählt:
Anfangsbedingung:
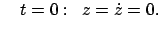
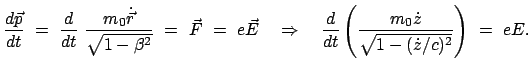 |
(1067) |
Diese Gleichung kann sofort nach der Zeit integriert werden. Die Anfangsbedingung verleiht
der Integrationskonstanten den Wert 0. Die resultierende Lösung wird quadriert und nach
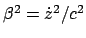 aufgelöst.
aufgelöst.
Diese Differentialgleichung kann durch Separation gelöst werden. Die Integration nach der
Zeit  wird durch folgende Substition ermöglicht:
wird durch folgende Substition ermöglicht:
Aus der Anfangsbedingung
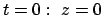 ergibt sich
ergibt sich
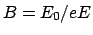 und damit die endgültige
Lösung:
und damit die endgültige
Lösung:
![$\displaystyle \underline{z = \frac{E_0}{eE} \left[ \sqrt{1 + \left(\frac{eE}{E_0} c t\right)^2} - 1 \right]. }$](img2725.gif) |
(1068) |
Diese Formel läßt sich auf folgende Form bringen:
Dazu dienen die neuen Variablen:
in denen die obige Bahngleichung die mathematische Form der Gleichung einer
Hyperbel hat. Deswegen heißt die Bewegung ''Hyperbelbewegung'', obwohl die Bahn
im Ortsraum eine Gerade ist.
Die obige Bahngleichung läßt zwei Näherungen zu: die eine für kleine Zeiten;
die andere für große Zeiten.
Nichtrelativistische Näherung: Für kleine Zeiten ist der zweite Term in der
Wurzel klein; man verwendet die ersten zwei Glieder der Binomialreihe:
und erhält die Lösung der klassischen Mechanik, weil die
Geschwindigkeit gering ist im Vergleich zu 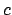 .
.
Extrem relativistische Näherung: Für große Zeiten ist der zweite Term der
Wurzel groß; man zieht diesen vor die Wurzel und verwendet dann wieder die Binomialreihe
für die resultierende Wurzel:
Das Teilchen läuft hier nahezu mit der Lichtgeschwindigkeit 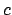 . Dies ergibt sich aus der
Ableitung des vorstehenden Ausdrucks nach der Zeit:
. Dies ergibt sich aus der
Ableitung des vorstehenden Ausdrucks nach der Zeit:
Die Kraft und das Potential sind dieselben wie im nichtrelativistischen Fall (§5.2):
Die Bewegungsgleichung lautet dann:
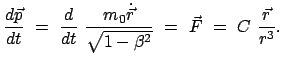 |
(1069) |
Daraus folgt durch vektorielle Multiplikation mit dem Ortsvektor
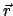 die Drehimpulserhaltung
die Drehimpulserhaltung
Damit ist auch hier die Bahn eben. Ebenso gilt der relativistische Energiesatz:
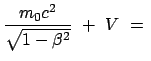 const. const. |
(1072) |
In beiden Erhaltungssätze werden Polarkoordinaten eingführt.
Das gibt für den Drehimpulssatz:
Statt der Zeit wird wieder das Azimuth 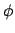 als unabhängige Variable eingeführt:
Damit werden auch
als unabhängige Variable eingeführt:
Damit werden auch
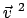 und
und 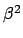 umgeschrieben;
umgeschrieben;
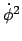 wird durch den
Drehimpuls ausgedrückt :
wird durch den
Drehimpuls ausgedrückt :
Statt  wird wieder die neue abhängige Variable
wird wieder die neue abhängige Variable 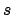 eingeführt:
eingeführt:
Das gibt letztlich:
Die neue Variable 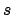 wird auch im Energiesatz eingeführt, der resultierende Ausdruck wird
quadriert und dann die vorstehende Beziehung eingesetzt.
wird auch im Energiesatz eingeführt, der resultierende Ausdruck wird
quadriert und dann die vorstehende Beziehung eingesetzt.
Der obige Ausdruck wird nach 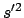 aufgelöst und dann zum Quadrat ergänzt.
Dazu werden folgende Abkürzungen eingeführt:
Dabei ist zu zeigen, daß
aufgelöst und dann zum Quadrat ergänzt.
Dazu werden folgende Abkürzungen eingeführt:
Dabei ist zu zeigen, daß
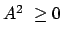 , d.h.
, d.h.
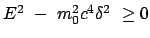 ist.
Dazu wird die Definition des relativistischen Drehimpulses herangezogen:
ist.
Dazu wird die Definition des relativistischen Drehimpulses herangezogen:
Nach der Theorie der quadratischen Gleichungen ist der obige Ausdruck in
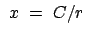 dann
dann 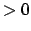 , wenn die damit gebildete quadratische Gleichung keine reelle Nullstelle aufweist.
Dies trifft aber zu, weil die Diskriminante
, wenn die damit gebildete quadratische Gleichung keine reelle Nullstelle aufweist.
Dies trifft aber zu, weil die Diskriminante 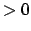 ist:
ist:
Beim Übergang zur letzten Zeile wurde noch folgende Umformung durchgeführt:
Die obige Differentialgleichung für 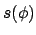 wird durch folgende Substitution
in eine solche für
wird durch folgende Substitution
in eine solche für 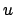 verwandelt. Letztere wird durch Ziehen der Wurzel und
Trennung der Variablen gelöst:
verwandelt. Letztere wird durch Ziehen der Wurzel und
Trennung der Variablen gelöst:
Geeignete Wahl von 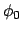 gibt:
Damit ergibt sich die endgültige Form der Bahngleichung:
gibt:
Damit ergibt sich die endgültige Form der Bahngleichung:
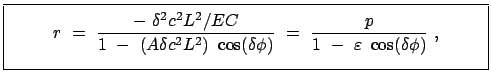 |
(1073) |
mit den Parametern
Aus der Form der Bahngleichung sieht man, daß für
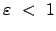 der
Radius
der
Radius  immer endlich bleibt, während er für
immer endlich bleibt, während er für
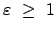 gegen Unendlich strebt. Aus dem Ausdruck für
gegen Unendlich strebt. Aus dem Ausdruck für
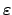 in der letzten Zeile ergibt sich, daß diese Unterscheidung zwischen den verschiedenen
Bahnformen wieder vom Wert der Gesamtenergie
in der letzten Zeile ergibt sich, daß diese Unterscheidung zwischen den verschiedenen
Bahnformen wieder vom Wert der Gesamtenergie 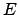 abhängt. Wegen des Hinzutretens
der Ruhenergie
abhängt. Wegen des Hinzutretens
der Ruhenergie 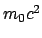 liegt die Grenze zwischen gebundenen und freien Zuständen nicht
mehr bei
liegt die Grenze zwischen gebundenen und freien Zuständen nicht
mehr bei 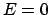 wie bei der nichtrelativistischen Lösung, sondern bei
wie bei der nichtrelativistischen Lösung, sondern bei
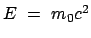 :
:
Die relativistische Massenveränderlichkeit bewirkt, daß die Bahnen der
gebundenen Zustände nicht mehr geschlossen sind, es erfolgt eine Periheldrehung;
deshalb bezeichnet man diese Bahnen als Rosettenbahnen.
Mathematisch wird die Periheldrehung durch den Faktor 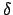 im Argument der cos-Funktion der obigen Bahngleichung verursacht:
im Argument der cos-Funktion der obigen Bahngleichung verursacht:
1. Perihel: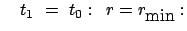 |
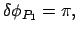 |
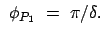 |
|
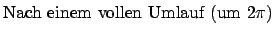  |
|
|
|
des Radiusvektors: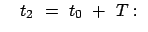 |
|
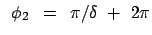 |
|
2. Perihel: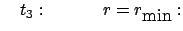 |
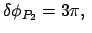 |
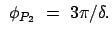 |
|
Für
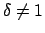 ist
ist
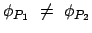 , dies entspricht einer
Drehung des Perihels um den Winkel
, dies entspricht einer
Drehung des Perihels um den Winkel
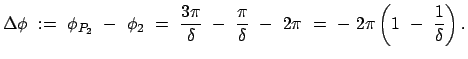 |
(1076) |
Aus der nichtrelativistischen Behandlung des Keplerproblems folgt:
Diese Formeln werden in die obige Formel für die Periheldrehung eingesetzt:
Abbildung:
Die Periheldrehung der relativistischen Keplerbewegung, Links: Die Bahn über mehrere
Perioden betrachtet. Rechts: Rote Bahn: Start im Perihel bis zum nächsten; blau: Verlauf vom 2.
bis zum 3. Perihel.
|
|
Die Periheldrehung ist umso größer, je kleiner 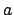 (Merkur) und je näher
(Merkur) und je näher
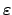 bei 1 liegt (Mars).
bei 1 liegt (Mars).
Die Präzession des Perihels des Planeten Merkur beträgt 5599.7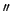 /Jahrhundert.
Aus den bekannten Störungen (vor allem die Wechselwirkung der Planeten untereinander und
über die Sonne) wurde eine Periheldrehung von 5557.0
/Jahrhundert.
Aus den bekannten Störungen (vor allem die Wechselwirkung der Planeten untereinander und
über die Sonne) wurde eine Periheldrehung von 5557.0 /Jahrhundert berechnet.
(Cl. M. Will: Theory and experiment in gravitational physics.
Cambridge University Press 1993).
Die Differenz von 47.7
/Jahrhundert berechnet.
(Cl. M. Will: Theory and experiment in gravitational physics.
Cambridge University Press 1993).
Die Differenz von 47.7 /Jahrhundert war schon um 1900 bekannt und
es wurde nach einer Erklärung gesucht.
Gl. (10.77) liefert nur 1/6 dieser Differenz. Aus der
allgemeinen Relativitätstheorie folgt ein Effekt der richtigen Größenordnung
(Einstein, Dicke).
/Jahrhundert war schon um 1900 bekannt und
es wurde nach einer Erklärung gesucht.
Gl. (10.77) liefert nur 1/6 dieser Differenz. Aus der
allgemeinen Relativitätstheorie folgt ein Effekt der richtigen Größenordnung
(Einstein, Dicke).
Die Bewegungsgleichung wird wie im nichtrelativistischen Fall (§3.4.3) behandelt:
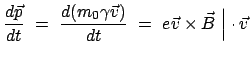 |
(1078) |
Dabei wurden Gln. (10.55) und (10.57) benützt. Es ergibt sich,
daß die Gesamtenergie 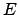 ,
damit auch
,
damit auch 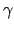 und der Betrag der Geschwindigkeit konstant sind. Daher kann
man in Gl. (10.78) durch
und der Betrag der Geschwindigkeit konstant sind. Daher kann
man in Gl. (10.78) durch
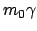 dividieren:
Man kann jede Lösung der nichtrelativistischen Bewegungsgleichung (§3.4.3,
Gl. (3.11)) in
eine der relativistischen Gl. (10.78) verwandeln, indem man in der ersteren die
Masse
dividieren:
Man kann jede Lösung der nichtrelativistischen Bewegungsgleichung (§3.4.3,
Gl. (3.11)) in
eine der relativistischen Gl. (10.78) verwandeln, indem man in der ersteren die
Masse  durch die bewegte Masse
durch die bewegte Masse
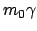 ersetzt. Insbesondere ergibt sich bei
Einschuß senkrecht zu den Feldlinien eines homogenen Magnetfeldes eine Kreisbahn mit Radius
ersetzt. Insbesondere ergibt sich bei
Einschuß senkrecht zu den Feldlinien eines homogenen Magnetfeldes eine Kreisbahn mit Radius 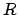 :
:
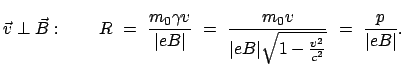 |
(1079) |
Je näher die Teilchengeschwindigkeit an 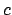 herankommt, desto schwerer wird
das Teilchen, desto größer die Fliehkraft, deswegen wächst der Radius
herankommt, desto schwerer wird
das Teilchen, desto größer die Fliehkraft, deswegen wächst der Radius 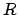 der
Bahn immer weiter.
der
Bahn immer weiter.
Gemäß der Lichtquantenhypothese (Einstein, 1905) besteht das Licht (wie jede
elektromagnetische Welle) aus Korpuskeln (Photonen), denen eine Energie
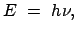 |
(1080) |
(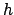 = Plancksches Wirkungsquantum) zukommt, und die sich mit der Geschwindigkeit
= Plancksches Wirkungsquantum) zukommt, und die sich mit der Geschwindigkeit
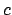 bewegen; das ist nur möglich, wenn ihre Ruhmasse
bewegen; das ist nur möglich, wenn ihre Ruhmasse 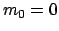 ist. Compton (1923)
begründete, daß diesen Photonen auch der Impuls
ist. Compton (1923)
begründete, daß diesen Photonen auch der Impuls
 |
(1081) |
( = Einheitsvektor in Richtung der Ausbreitung der ebenen Welle) zukommt.
Aus (10.53), (10.54) und (10.57) ergibt sich:
= Einheitsvektor in Richtung der Ausbreitung der ebenen Welle) zukommt.
Aus (10.53), (10.54) und (10.57) ergibt sich:
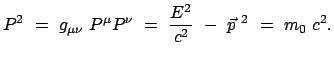 |
(1082) |
Daraus folgt mit 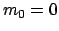 und mit (10.80) der Betrag von (10.81).
Mittels dieser beiden Gleichungen ist es möglich, Photonen dem relativistischen Energie- und
Impulssatz zu unterwerfen und sie in die relativistische Kinematik einzubeziehen.
Der Erfolg dieser Vorgangsweise ist eine Bestätigung der Hypothesen
(10.80) und (10.81).
und mit (10.80) der Betrag von (10.81).
Mittels dieser beiden Gleichungen ist es möglich, Photonen dem relativistischen Energie- und
Impulssatz zu unterwerfen und sie in die relativistische Kinematik einzubeziehen.
Der Erfolg dieser Vorgangsweise ist eine Bestätigung der Hypothesen
(10.80) und (10.81).
Abbildung 10.11:
a) Der Comptoneffekt. b) Die Paarerzeugung
|
[]
![\includegraphics[scale=0.66]{k10_compton_effekt}](img2852.gif) []
[]
![\includegraphics[scale=0.66]{k10_paarerzeugung}](img2853.gif) |
Beim Comptoneffekt fallen Röntgenstrahlen der Frequenz 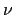 auf fast freie, nahezu
ruhende Elektronen in einem Paraffinblock, werden an diesen zur Frequenz
auf fast freie, nahezu
ruhende Elektronen in einem Paraffinblock, werden an diesen zur Frequenz 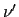 gestreut und verleihen diesen eine Geschwindigkeit
gestreut und verleihen diesen eine Geschwindigkeit 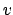 . Da der 1922 entdeckte Effekt
mittels des Energie- und Impulssatzes der relativistischen Mechanik hergeleitet
werden kann, bestätigt er die Vorstellungen von Gln. (10.80) und (10.81).
. Da der 1922 entdeckte Effekt
mittels des Energie- und Impulssatzes der relativistischen Mechanik hergeleitet
werden kann, bestätigt er die Vorstellungen von Gln. (10.80) und (10.81).
Der Energie vor und nach dem Stoß ist gleich:
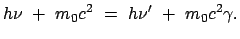 |
(1083) |
Statt des Impulssatzes in vektorieller Form wird für die Impulse in obiger
Abb. 10.11(a) der Kosinussatz verwendet:
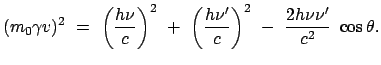 |
(1084) |
Wird Gl. (10.83) quadriert und davon Gl. (10.84) abgezogen, ergibt sich
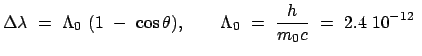 m m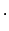 |
(1085) |
Das Experiment bestätigt die Winkelabhängigkeit der Wellenlängenänderung
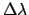 und den numerischen Wert der Comptonwellenlänge
und den numerischen Wert der Comptonwellenlänge 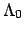 des Elektrons.
des Elektrons.
Bei der Paarerzeugung wird ein Photon in ein Teilchen-, Antiteilchenpaar
(Ladungserhaltung!) (Abb. 10.11(b)) verwandelt. Diese Reaktion ist im
freien Raum nicht möglich, denn es können Energie- und Impulssatz nicht gleichzeitig
erfüllt werden:
Gl. (10.86) und die erste der Impulsgleichungen, Gl. (10.87),
widersprechen sich, da
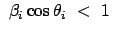 ist.
ist.
Abbildung 10.12:
Paarerzeugung bei Anwesenheit eines dritten Teilchens
|
![\includegraphics[scale=0.66]{k10_paarerzeugung_impulsdiag}](img2877.gif) |
Die Paarerzeugung ist möglich, wenn an der Reaktion noch ein drittes Teilchen teilnimmt,
das den Impuls aufnimmt. Meist ist dies ein Atomkern, der wesentlich schwerer ist als das
erzeugte Elektron-, Positronpaar. Daher ist die Bewegung dieses schweren Partners
nichtrelativistisch.
 Ruhmasse des Kerns;
Ruhmasse des Kerns;  Ruhmasse des Elektrons, Positrons;
Ruhmasse des Elektrons, Positrons;
 .
.
Der Impulssatz gibt:
Gln. (10.88) bis (10.90) sind ein System von 3 Gleichungen zur Bestimmung der
6 Unbekannten  ,
, 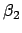 ,
, 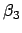 ,
, 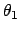 ,
, 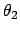 ,
, 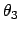 . Man kann es,
z.B., so auflösen, daß man die drei
. Man kann es,
z.B., so auflösen, daß man die drei
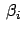 als Funktionen der drei
Streuwinkel
als Funktionen der drei
Streuwinkel
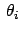 bekommt. Wir lösen nur den Spezialfall, daß
das leichte Teilchenpaar symmetrisch ausläuft:
(10.90) ist dann trivial erfüllt, (10.88) und (10.89) geben dann:
bekommt. Wir lösen nur den Spezialfall, daß
das leichte Teilchenpaar symmetrisch ausläuft:
(10.90) ist dann trivial erfüllt, (10.88) und (10.89) geben dann:
Die Gleichheit des ersten und dritten Terms der obigen Zeile bestätigt man durch Ausrechnen.
Für 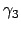 verwendet man den Ausdruck in der vorletzten Gleichung links,
verwendet man den Ausdruck in der vorletzten Gleichung links,
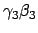 den rechts. Die untersrichenen Terme dienen zur Bestimmung von
den rechts. Die untersrichenen Terme dienen zur Bestimmung von 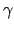 .
.
Nach Quadrieren geben sie:
Wegen der Kleinheit von 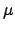 , wird obige Gleichung iterativ nach
, wird obige Gleichung iterativ nach 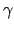 aufgelöst.
Die nullte Näherung ist:
aufgelöst.
Die nullte Näherung ist:
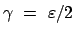 . Die erste Näherung ist:
In dieser Näherung ergibt sich für die Energie des Elektrons (ebenso des
Positrons) und für die kinetische Energie des Kerns:
. Die erste Näherung ist:
In dieser Näherung ergibt sich für die Energie des Elektrons (ebenso des
Positrons) und für die kinetische Energie des Kerns:
Abbildung 10.13:
Zerfall eines neutralen Pions in zwei Gammaquanten; links vom Laborsystem
aus betrachtet, rechts im Schwerpunktsystem.
|
![\includegraphics[scale=0.69]{k10_pion_zerfall_ls_ss}](img2916.gif) |
Ein neutrales Pion (Pi-Meson) ist instabil (mittlere Lebensdauer im Eigensystem
(
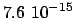 s) und zerfällt hauptsächlich in zwei Gammaquanten:
s) und zerfällt hauptsächlich in zwei Gammaquanten:
Deren Energie soll berechnet werden. Das Pion läuft im Laborsystem (LS) mit
der Geschwindigkeit 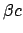 ein. Es ist am zweckmäßigsten, den Vorgang im Eigensystem
des Pions (SS, dort ist der Gesamtimpuls der auslaufenden Photonen Null; Abb. 10.13(b)
zu berechnen und ins LS (Abb. 10.13(a)) rückzutransformieren. Für den Energie-Impulsvektor
gelten die gleichen Lorentztransformationen (10.25) wie für den Raum-Zeitvektor:
ein. Es ist am zweckmäßigsten, den Vorgang im Eigensystem
des Pions (SS, dort ist der Gesamtimpuls der auslaufenden Photonen Null; Abb. 10.13(b)
zu berechnen und ins LS (Abb. 10.13(a)) rückzutransformieren. Für den Energie-Impulsvektor
gelten die gleichen Lorentztransformationen (10.25) wie für den Raum-Zeitvektor:
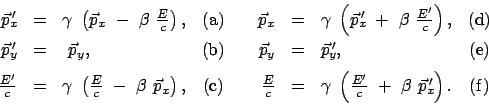 |
(1093) |
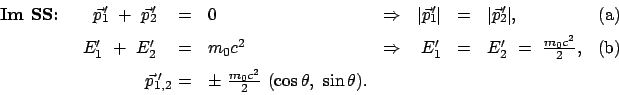 |
(1094) |
Im LS: |
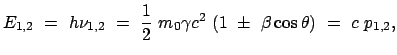 |
(a) |
|
| |
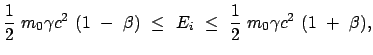 |
(b) |
(1095) |
| |
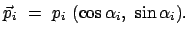 |
(c) |
(1096) |
Aus (10.94a) - (10.94c) berechnet man mittels (10.93d)
- (10.93f) die Energien und Impulse der
beiden Photonen im LS und den Schwankungsbereich der Energien. Aus (10.93a) und
(10.94f) folgt der Zusammenhang zwischen 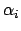 und
und 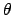 ,
aus (10.94a) der Zusammenhang zwischen dem Winkel
,
aus (10.94a) der Zusammenhang zwischen dem Winkel 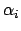 und der
Photonenenergie.
und der
Photonenenergie.
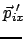 |
 |
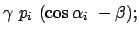 |
(1097) |
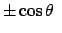 |
 |
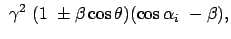 |
(1098) |
| |
 |
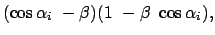 |
(1099) |
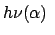 |
 |
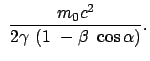 |
(10100) |
Für die Umwandlung von Pionen in 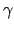 -Quanten, die durch den obigen Zerfall bewirkt wird,
läßt sich ein Wirkungsquerschnitt angeben. Das Pion hat Spin 0 und ist daher sphärisch
symmetrisch; in seinem Eigensystem gibt es keine ausgezeichnete Richtung. Daher muß der
Wirkunsquerschnitt für diese Umwandlung von den Winkeln unabhängig sein:
-Quanten, die durch den obigen Zerfall bewirkt wird,
läßt sich ein Wirkungsquerschnitt angeben. Das Pion hat Spin 0 und ist daher sphärisch
symmetrisch; in seinem Eigensystem gibt es keine ausgezeichnete Richtung. Daher muß der
Wirkunsquerschnitt für diese Umwandlung von den Winkeln unabhängig sein:
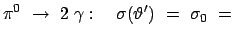
const.
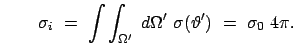
Im Laborsystem haben die Pionen im allgemeinen eine hohe Geschwindigkeit; dadurch laufen die
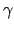 -Quanten bevorzugt in die Vorwärtsrichtung; der Wirkungsquerschnitt hat dann eine starke
Winkelabhängigkeit. Diese läßt sich durch eine Lorentztransformation berechnen.
Der Winkel zwischen der Richtung der einlaufenden Pionen (=
-Quanten bevorzugt in die Vorwärtsrichtung; der Wirkungsquerschnitt hat dann eine starke
Winkelabhängigkeit. Diese läßt sich durch eine Lorentztransformation berechnen.
Der Winkel zwischen der Richtung der einlaufenden Pionen (= 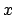 -Achse) und dem auslaufenden
-Achse) und dem auslaufenden
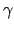 -Quant wird hier mit
-Quant wird hier mit  bezeichnet und ist am Abschluss mit dem Winkel
bezeichnet und ist am Abschluss mit dem Winkel
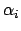 des betrachtenten Photons zu identifizieren.
Die Lorentzkontraktion (10.34):
verändert das Volumselement folgendermaßen:
In Bezug auf das Transformationsverhalten ist
des betrachtenten Photons zu identifizieren.
Die Lorentzkontraktion (10.34):
verändert das Volumselement folgendermaßen:
In Bezug auf das Transformationsverhalten ist
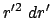 zu
zu 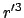 gleichwertig.
Wir können daher für den Raumwinkel
gleichwertig.
Wir können daher für den Raumwinkel 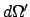 und damit auch für den Wirkungsquerschnitt
folgende Umrechung von Pioneigensystem in das Laborsystem vornehmen:
und damit auch für den Wirkungsquerschnitt
folgende Umrechung von Pioneigensystem in das Laborsystem vornehmen:
Nun gilt aber:
Aus den beiden vorhergehenden Gleichungen folgt nun für den Wirkungsquerschnitt des
Zerfalls
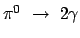 im Laborsystem:
im Laborsystem:
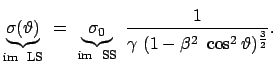 |
(10101) |
Die Abbildungen 10.14 zeigen, daß der differentielle Wirkungsquerschnitt im
Laborsystem Maxima in Vorwärts- und Rückwärtsrichtung aufweist; diese nehmen mit steigender
Energie zu.
Der integrale Wirkungsquerschnitt hat im LS den gleichen Wert wie im SS, wie es sein
muß:
Abbildung 10.14:
Der differentielle Wirkungsquerschnitt des Zerfalls
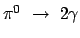 im Laborsystem.
im Laborsystem.
![\includegraphics[width=16cm]{K10Pi0De}](img2947.gif) |
LITERATUR:
L. Bergmann, Cl.Schäfer: Lehrbuch der Experimentalphysik III (Optik), Kap.IX.
(deGruyter, 6. Aufl., Berlin 1974)
M.Born: Die Relativitätstheorie Einsteins (Heidelberger Taschenbuch)
A.Einstein: Über spezielle und allgemeine Relativitätstheorie
(Sammlung Vieweg)
E. Schmutzer: Relativitätstheorie aktuell. Teubner Studienbücher 1996.
Cl.Schäfer: Einführung in die theoretische Physik III1, Kap.14 (de Gruyter)
R.Becker, F.Sauter: Theorie der Elektrizität, Kap. E (Teubner)
J.H.Smith: The Theory of Relativity (Benjamin 1965)
R.U.Sexl, H.K.Urbantke: Relativität, Gruppen, Teilchen; Kap. 1,2
(Springer Verlag 1976)
R.K.Pathria: The Theory of Relativity
(Pergamon Press 1974)
W. Lucha, M. Regler: Elementarteilchenphysik, Theorie und Experiment. Schulbuch- und Lehrmittelverlag
Paul Sappl, Kufstein 1997.
Christian Sommer
2003-01-27
![]() ) gilt: Man kann aufgrund
mechanischer Experimente keine Aussagen über den Bewegungszustand eines
gleichförmig bewegten Systems, in dem man sich befindet, machen.
) gilt: Man kann aufgrund
mechanischer Experimente keine Aussagen über den Bewegungszustand eines
gleichförmig bewegten Systems, in dem man sich befindet, machen.
![]() aus betrachtet:
aus betrachtet:
![]() ) groß gegenüber der zu messenden
Schallgeschwindigkeit ist) vom Anfang zum Ende der Strecke (Messung der
''Einweggeschwindigkeit''). Ein derartiges Vorgehen ist bei der Messung
der Vakuumlichtgeschwindigkeit
) groß gegenüber der zu messenden
Schallgeschwindigkeit ist) vom Anfang zum Ende der Strecke (Messung der
''Einweggeschwindigkeit''). Ein derartiges Vorgehen ist bei der Messung
der Vakuumlichtgeschwindigkeit ![]() nicht möglich, da man keine Art von
Signalen kennt, deren Ausbreitungsgeschwindigkeit groß gegen
nicht möglich, da man keine Art von
Signalen kennt, deren Ausbreitungsgeschwindigkeit groß gegen ![]() ist.
Man ist daher gezwungen, das Lichtsignal, dessen Ausbreitungsgeschwindigkeit
gemessen werden soll, am Ende der Messtrecke zu reflektieren und kann
daher nur die Laufzeit für Hin- und Rückweg messen (''Zweiweggeschwindigkeit'').
Das wichtigste der diesbezüglichen Experimente war der Michelsonversuch:
(Im Äther ist die Lichtgeschwindigkeit gemäß der damaligen Ansicht
ist.
Man ist daher gezwungen, das Lichtsignal, dessen Ausbreitungsgeschwindigkeit
gemessen werden soll, am Ende der Messtrecke zu reflektieren und kann
daher nur die Laufzeit für Hin- und Rückweg messen (''Zweiweggeschwindigkeit'').
Das wichtigste der diesbezüglichen Experimente war der Michelsonversuch:
(Im Äther ist die Lichtgeschwindigkeit gemäß der damaligen Ansicht ![]() ,
für andere Systeme muß man gemäß (10.3) umrechnen, (Abb. 10.2(a)).
Der gesamte Meßapparat bewegt
,
für andere Systeme muß man gemäß (10.3) umrechnen, (Abb. 10.2(a)).
Der gesamte Meßapparat bewegt
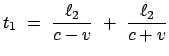
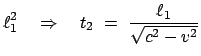
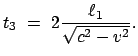
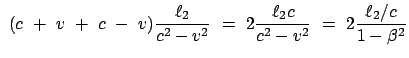
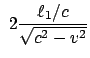
![$\displaystyle \Delta t := t_3 - t_1 = \frac{2}{c}\left[\frac{\ell_1}{\sqrt{c^2 - v^2}} - \
\frac{\ell_2}{1 - \beta^2}\right].
$](img2428.gif)
![$\displaystyle \Delta t' := t'_3 - t'_1 = \frac{2}{c}\left[\frac{\ell_1}{1 - \beta^2} - \
\frac{\ell_2}{\sqrt{1 -\beta^2}} \right].$](img2430.gif)
![$\displaystyle \Delta t' - \Delta t = \frac{2}{c} \
\left[\frac{ \ell...
... +
\frac{\ell_2}{1 - \beta^2} - \frac{\ell_2}{\sqrt{1 - \beta^2}}\right]$](img2432.gif)
![$\displaystyle 2 \frac{\ell_1 + \ell_2}{c} \left[ \frac{1}{1 - \beta^2} - \
\frac{1}{\sqrt{1 - \beta^2}} \right].$](img2433.gif)
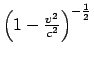 ; Längen in den
transversalen Richtungen bleiben unverändert. Dann erhält man in den obigen
Gleichungen für
; Längen in den
transversalen Richtungen bleiben unverändert. Dann erhält man in den obigen
Gleichungen für
![]() : Koordinaten
: Koordinaten
![]() Zeit
Zeit ![]() ;
;
![]() : Koordinaten
: Koordinaten
![]() Zeit
Zeit ![]() .
.
![]() liege in der
1-Achse von
liege in der
1-Achse von ![]() :
:
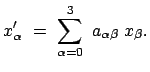
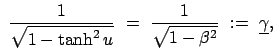
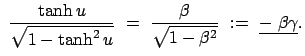
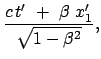
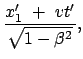
![]() und
und
![]() enthalten obige Gleichungen die
Galileitransformationen, Gln. (10.1) - (10.3).
enthalten obige Gleichungen die
Galileitransformationen, Gln. (10.1) - (10.3).
![]() ist
ist ![]() das ''Ruhesystem'' und
das ''Ruhesystem'' und ![]() das ''bewegte System'';
für einen Beobachter B
das ''bewegte System'';
für einen Beobachter B![]() in
in ![]() verhält es sich gerade umgekehrt. Wir nehmen von den
obigen Lorentztransformationen nur die Gleichung für die zur Systembewegung parallele
Komponente und die Zeit.
verhält es sich gerade umgekehrt. Wir nehmen von den
obigen Lorentztransformationen nur die Gleichung für die zur Systembewegung parallele
Komponente und die Zeit.
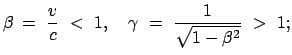
![]() vom Ursprung
vom Ursprung
![]() ein Lichtblitz ausgesendet.
In jedem System befindet sich bei jeder Uhr ein Spiegel,
der den Lichtblitz zum Ursprung reflektiert. Die Hälfte der ganzen Laufzeit ist
dann die Zeit, die die Uhr in dem Moment anzeigen muß,
als bei ihr der Lichtblitz eingetroffen ist.
ein Lichtblitz ausgesendet.
In jedem System befindet sich bei jeder Uhr ein Spiegel,
der den Lichtblitz zum Ursprung reflektiert. Die Hälfte der ganzen Laufzeit ist
dann die Zeit, die die Uhr in dem Moment anzeigen muß,
als bei ihr der Lichtblitz eingetroffen ist.
![]() stellt fest, daß zwei Ereignisse an verschiedenen Orten seines Systems
gleichzeitig eingetreten sind:
stellt fest, daß zwei Ereignisse an verschiedenen Orten seines Systems
gleichzeitig eingetreten sind:
![]() -Achse an allen Orten
Uhren aufgestellt und synchronisiert (in seinem System ist ja der
Begriff der Gleichzeitigkeit sinnvoll). Die Uhren des Systems
-Achse an allen Orten
Uhren aufgestellt und synchronisiert (in seinem System ist ja der
Begriff der Gleichzeitigkeit sinnvoll). Die Uhren des Systems ![]() (dort ruhend) fliegen an denen des Systems
(dort ruhend) fliegen an denen des Systems ![]() vorbei und werden mit den
jeweils gegenüberliegenden Uhren von
vorbei und werden mit den
jeweils gegenüberliegenden Uhren von ![]() verglichen.
Dies ergibt zu den Zeitpunkten
verglichen.
Dies ergibt zu den Zeitpunkten ![]() bzw.
bzw.
![]() :
Für einen Uhrenvergleich zum Nachweis der Zeitdilatation benötigt
man mindestens 3 Uhren (z.B. in
:
Für einen Uhrenvergleich zum Nachweis der Zeitdilatation benötigt
man mindestens 3 Uhren (z.B. in ![]() in
in ![]() ; in
; in ![]() in
in
![]() und
und ![]() ).
).
![]() , d.h.
, d.h.
![]() , fliegt,
dann mißt man von der Erde aus anstelle von
, fliegt,
dann mißt man von der Erde aus anstelle von
![]() s
die längere mittlere Lebensdauer von
s
die längere mittlere Lebensdauer von
![]() s.
Diese Zeit reicht aus, um eine Strecke von 6 km zurückzulegen.
Dieser Effekt wurde bei Beobachtungen genau untersucht. Wegen des
statistischen Charakters des Zerfallsgesetzes ist dieses Experiment
nicht so einfach durchzuführen, wie in der obigen Abbildung schematisiert.
Es wurden die Myonenzahlen in verschiedenen Höhen registriert und
daraus die Lebensdauer deduziert.(s. J. H. Smith, §3.5).
s.
Diese Zeit reicht aus, um eine Strecke von 6 km zurückzulegen.
Dieser Effekt wurde bei Beobachtungen genau untersucht. Wegen des
statistischen Charakters des Zerfallsgesetzes ist dieses Experiment
nicht so einfach durchzuführen, wie in der obigen Abbildung schematisiert.
Es wurden die Myonenzahlen in verschiedenen Höhen registriert und
daraus die Lebensdauer deduziert.(s. J. H. Smith, §3.5).
![]() und fliegt gleichförmig bis zu einem
und fliegt gleichförmig bis zu einem
![]() entfernten Himmelskörper, kehrt dort um
und fliegt gleichförmig wieder zurück.
entfernten Himmelskörper, kehrt dort um
und fliegt gleichförmig wieder zurück.
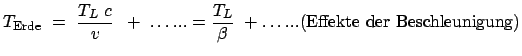

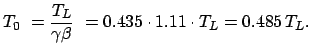
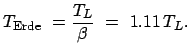
![]() ;
dieses präzediert im Magnetfeld des Speicherringes
s. Abb. 10.6(a). Die Präzessionsgeschwindigkeit
gestattet es, die Größe von
;
dieses präzediert im Magnetfeld des Speicherringes
s. Abb. 10.6(a). Die Präzessionsgeschwindigkeit
gestattet es, die Größe von ![]() und damit des magnetischen Moments zu bestimmen.
Die Präzession kann beobachtet werden, weil die Emission der Elektronen bzw. Positronen beim
Zerfall des Myons
und damit des magnetischen Moments zu bestimmen.
Die Präzession kann beobachtet werden, weil die Emission der Elektronen bzw. Positronen beim
Zerfall des Myons
![]() ruht ein Stab der Länge
ruht ein Stab der Länge ![]() , d.h. ein Beobachter in
, d.h. ein Beobachter in ![]() beschreibt
die Endpunkte des Stabes mit den Koordinaten:
beschreibt
die Endpunkte des Stabes mit den Koordinaten:
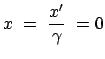 und
und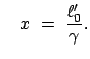
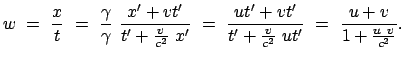
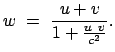
![]() fließt mit Geschwindigkeit
fließt mit Geschwindigkeit ![]() .
In der ruhenden Flüssigkeit ist die Lichtgeschwindigkeit
.
In der ruhenden Flüssigkeit ist die Lichtgeschwindigkeit ![]() .
Die Lichtgeschwindigkeit im Labor (bei fließendem Wasser) beträgt:
.
Die Lichtgeschwindigkeit im Labor (bei fließendem Wasser) beträgt:
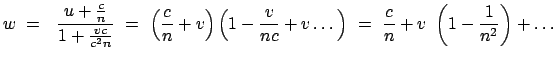
![]() -Achse ist. Nun sei der Vektor der Geschwindigkeit von S' relativ zu S
gleich
-Achse ist. Nun sei der Vektor der Geschwindigkeit von S' relativ zu S
gleich ![]() . Um die Gesetzmäßigkeit anwenden zu können, die sich in den Formeln
(10.25) zeigt, zerlegen wir den Vektor
. Um die Gesetzmäßigkeit anwenden zu können, die sich in den Formeln
(10.25) zeigt, zerlegen wir den Vektor ![]() in eine Komponente parallel zu
in eine Komponente parallel zu ![]() und in eine senkrecht zu
und in eine senkrecht zu ![]() . Die senkrechte Komponente bleibt unverändert.
Für die Zeittransformation ist statt
. Die senkrechte Komponente bleibt unverändert.
Für die Zeittransformation ist statt ![]() die Projektion von
die Projektion von ![]() auf
auf ![]() zu setzen.
zu setzen.
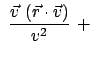
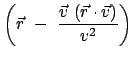
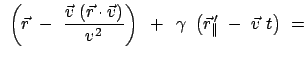
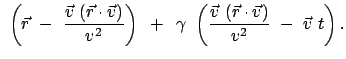
![]() eine system- und ortsabhängige Größe
ist, muß sie zusammen mit den Ortskoordinaten
eine system- und ortsabhängige Größe
ist, muß sie zusammen mit den Ortskoordinaten ![]() ,
, ![]() ,
, ![]() zur systembezogenen Beschreibung
eines physikalischen Ereignisses herangezogen werden. Es ist zweckmäßig,
die Zeit
zur systembezogenen Beschreibung
eines physikalischen Ereignisses herangezogen werden. Es ist zweckmäßig,
die Zeit ![]() als 4. Komponente eines Vektors zu schreiben. Damit diese 4. Komponente
die gleiche Dimension hat wie die drei ersten Komponenten, wird der Lichtweg
als 4. Komponente eines Vektors zu schreiben. Damit diese 4. Komponente
die gleiche Dimension hat wie die drei ersten Komponenten, wird der Lichtweg
![]() statt der reinen Zeit gewählt. Der Raum dieser
vierdimensionalen Vektoren heißt die Minkowskiwelt. Diese wird unten
in der rechten Spalte eingeführt. Zum Vergleich werden die analogen bekannten
Formeln der üblichen dreidimensionalen Vektorrechnung in der linken Spalte angegeben.
Die Minkowskiwelt ist nicht euklidisch. Deswegen gibt es hier ko- (Index unten) und
kontravariante Koordinaten (Index oben); und dies muß bei der Definition des skalaren
Produktes berücksichtigt werden.
statt der reinen Zeit gewählt. Der Raum dieser
vierdimensionalen Vektoren heißt die Minkowskiwelt. Diese wird unten
in der rechten Spalte eingeführt. Zum Vergleich werden die analogen bekannten
Formeln der üblichen dreidimensionalen Vektorrechnung in der linken Spalte angegeben.
Die Minkowskiwelt ist nicht euklidisch. Deswegen gibt es hier ko- (Index unten) und
kontravariante Koordinaten (Index oben); und dies muß bei der Definition des skalaren
Produktes berücksichtigt werden.
![]() heißt die Eigenzeit; sie wird mit einer Uhr gemessen, die im Ursprung,
heißt die Eigenzeit; sie wird mit einer Uhr gemessen, die im Ursprung, ![]() des Systems des beobachteten Teilchens ruht.
Die Definition des inneren Produkts zweier Vierervektoren gemäß (10.40) wird verständlich,
wenn man auf Gl. (10.42) schaut: Das innere Produkt zweier Vektoren muß invariant bleiben,
im dreidimensionalen Ortsraum beim Drehungen, in der Minkowskiwelt bei Drehungen im
Ortsraum, insbesondere auch bei Lorentztransformationen. Bei letzteren muß aber die Wellenfront
eines Lichtblitzes immer eine Kugel sein, d.h. es muß
des Systems des beobachteten Teilchens ruht.
Die Definition des inneren Produkts zweier Vierervektoren gemäß (10.40) wird verständlich,
wenn man auf Gl. (10.42) schaut: Das innere Produkt zweier Vektoren muß invariant bleiben,
im dreidimensionalen Ortsraum beim Drehungen, in der Minkowskiwelt bei Drehungen im
Ortsraum, insbesondere auch bei Lorentztransformationen. Bei letzteren muß aber die Wellenfront
eines Lichtblitzes immer eine Kugel sein, d.h. es muß
![]() invariant bleiben.
Das zwingt uns zu einer entsprechenden Definition des inneren Produkts wie oben in
Gl. (10.41) mittels eines ko- oder kontravarianten Maßtensors. Dieser ist hier
immer diagonal und hat konstante Elemente:
invariant bleiben.
Das zwingt uns zu einer entsprechenden Definition des inneren Produkts wie oben in
Gl. (10.41) mittels eines ko- oder kontravarianten Maßtensors. Dieser ist hier
immer diagonal und hat konstante Elemente:
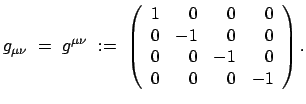
![]() im
Raum-Zeit-Vektor eine vierte rein imaginäre Komponente einzuführen, also diesen
Vektor folgendermaßen zu definieren:
im
Raum-Zeit-Vektor eine vierte rein imaginäre Komponente einzuführen, also diesen
Vektor folgendermaßen zu definieren:
![$\displaystyle \left( \begin{array}{c} x^{'}_{1} [2mm] x^{'}_{2} [2mm] x^{'}_{3} [2mm] \end{array} \right) =
$](img2625.gif)
![$\displaystyle = \left( \begin{array}{ccc} a_{11} & a_{12} & a_{13} [2mm] a...
...array}{c} x_{1} [2mm] x_{2} [2mm] x_{3} [2mm] \end{array} \right) .
$](img2626.gif)
![]() sollen
invariant sein gegenüber einer linearen Koordinatentransformation. Ebenso soll die Norm
sollen
invariant sein gegenüber einer linearen Koordinatentransformation. Ebenso soll die Norm
![]() des Raum-Zeit-Vektors invariant gegenüber einer Lorentztransformation sein.
des Raum-Zeit-Vektors invariant gegenüber einer Lorentztransformation sein.
![]() ist das
Differential der Eigenzeit, umgerechent gemäß Gl. (10.32).
ist das
Differential der Eigenzeit, umgerechent gemäß Gl. (10.32).
![]() nicht ganz angepaßt sind, weil
nicht ganz angepaßt sind, weil ![]() selbst eine
Koordinate ist. Man muß nach einem invariaten Parameter ableiten.
Dafür wird die Eigenzeit
selbst eine
Koordinate ist. Man muß nach einem invariaten Parameter ableiten.
Dafür wird die Eigenzeit ![]() verwendet.
Man betrachtet den Raum-Zeit-Vektor
verwendet.
Man betrachtet den Raum-Zeit-Vektor ![]() als Funktion von
als Funktion von ![]() und
bildet die Ableitung nach
und
bildet die Ableitung nach ![]() , dies gibt die
Vierergeschwindigkeit U. Die Ableitungen nach
, dies gibt die
Vierergeschwindigkeit U. Die Ableitungen nach ![]() haben jedoch hauptsächlich theoretische Bedeutung, da z.B.
Messungen meist im Ruhsystem des Beobachters, also im Laborsystem,
ausgeführt werden. Man kann aber für
haben jedoch hauptsächlich theoretische Bedeutung, da z.B.
Messungen meist im Ruhsystem des Beobachters, also im Laborsystem,
ausgeführt werden. Man kann aber für ![]() den Ausdruck
den Ausdruck ![]() substituieren (s. Gl. (10.32)).
substituieren (s. Gl. (10.32)).
![]() . Im Eigensystem des Teilchens gilt:
. Im Eigensystem des Teilchens gilt:
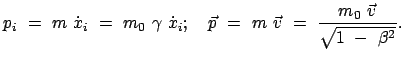
![$\displaystyle E = m c^2 = m_0 c^2 \big[1 - \beta^2 \big]^{-1/2} =...
... + ... \Big] = m_0 c^2 + \
\frac{1}{2} m_0 \vec{v}^{ 2} + ...
$](img2685.gif)
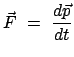 mit
mit![]() , machen zu können, wird zuerst eine Hilfsrelation abgeleitet.
Dazu werden die Vierergeschwindigkeit und die Viererkraft znächst im Ruhesystem
angesetzt. Es zeigt sich, daß ihr skalares Produkt Null ist. Da dieses eine
Lorentzinvariante ist, ist das Produkt in jedem System Null. Daraus kann man
eine Formel für
, machen zu können, wird zuerst eine Hilfsrelation abgeleitet.
Dazu werden die Vierergeschwindigkeit und die Viererkraft znächst im Ruhesystem
angesetzt. Es zeigt sich, daß ihr skalares Produkt Null ist. Da dieses eine
Lorentzinvariante ist, ist das Produkt in jedem System Null. Daraus kann man
eine Formel für
![]() ableiten:
ableiten:
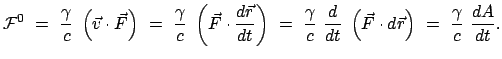
![]() , die ein Potential
, die ein Potential ![]() besitzt:
besitzt:
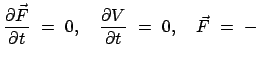 grad
grad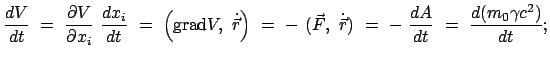
![$\displaystyle \frac{d}{dt} \Big[ V + m_0 \gamma c^2 \Big] = 0.
$](img2707.gif)
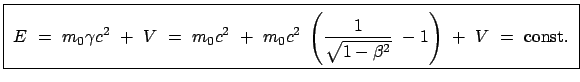
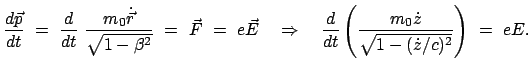
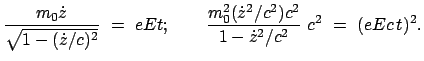
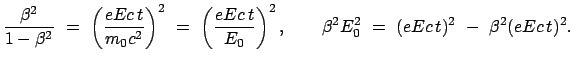
![$\displaystyle \beta^2 = \left[ 1 + \left(\frac{E_0}{eEc t}\right)^2 \right]^{-1} < 1,$](img2715.gif)
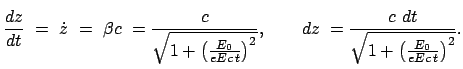
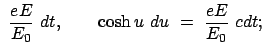
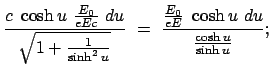
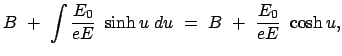
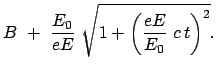
![$\displaystyle \left[ \frac{eE}{E_0} z + 1 \right]^2 = 1 + \left(\...
...ight)^2
\quad \Longleftrightarrow \quad \bar{z}^2 - c \bar{t}^2 = -1.
$](img2726.gif)
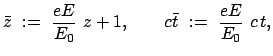
![$\displaystyle z = \frac{E_0}{eE} \left[ 1 + \frac{1}{2} \left(\frac{eE}...
...
c t\right)^2 + \dots \right] = \
\frac{eE}{m} \frac{t^2}{2} + \dots
$](img2728.gif)
![$\displaystyle \frac{E_0}{eE} \left[ \left(\frac{eE}{E_0} c t\right) \sqr...
...t \frac{eE}{E_0} + \frac{1}{2} \frac{E_0}{ eE c t} - \dots - 1 \Big]$](img2729.gif)
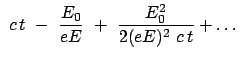
![$\displaystyle \dot{z} = c \left[ 1 - \frac{E_0^2}{2 (eE)^2 (c t)^2} + \dots \right] .
$](img2731.gif)
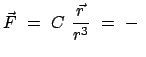 grad
grad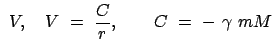 oder
oder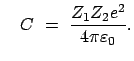
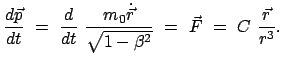
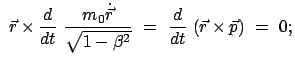
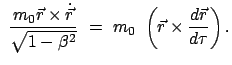
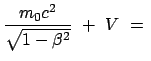 const.
const.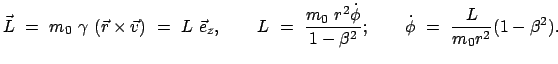
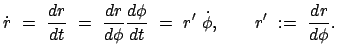
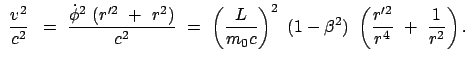
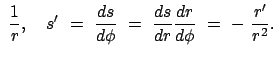
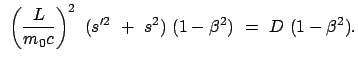
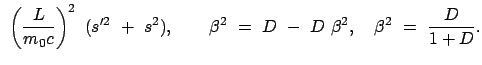
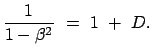
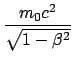
![$\displaystyle \frac{m_0^2 c^4}{1 - \beta^2} = \
m_0^2 c^4 \left[ 1 + \left(\frac{L}{m_0 c}\right)^2 (s^{'2} + s^2) \right] ;$](img2761.gif)
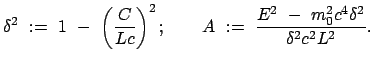
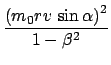 mit
mit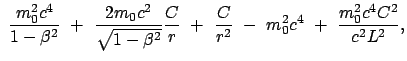

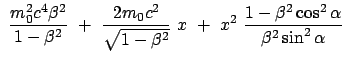
![$\displaystyle - b^2 + a d = \frac{m_0^2 c^4}{1 - \beta^2} \Big[ 1 \...
...alpha}{\beta^2 \sin^2\alpha} \Big] = \
m_0^2 c^4 \cot^2\alpha \ge 0 .
$](img2778.gif)
![$\displaystyle \left(\frac{E}{Lc}\right)^2 - \left(\frac{m_0 c}{L}\right)^2
...
...2 \left[ 1 - \left(\frac{C}{Lc}\right)^2 \right] -
\frac{2 E C s}{L^2 c^2},$](img2782.gif)
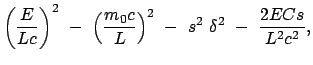
![$\displaystyle \left(\frac{E}{Lc}\right)^2 - \left(\frac{m_0 c}{L}\right)^2 ...
...2} \right)^2
- \delta^2 \left(\frac{EC}{(\delta c L)^2} \right)^2 \right] ,$](img2784.gif)
![$\displaystyle \left(\frac{E}{Lc}\right)^2 - \left(\frac{m_0 c}{L}\right)^2 ...
...right]^2 - \
\delta^2 \left[ s + \frac{EC}{(\delta c L)^2} \right]^2 ,$](img2785.gif)
![$\displaystyle A^2 - \delta^2 \left[ s + \frac{EC}{(\delta c L)^2} \right]^2 .$](img2786.gif)
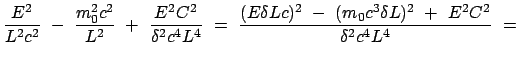
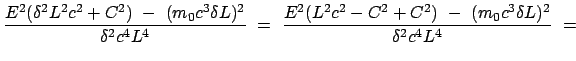

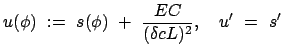
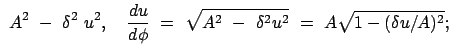
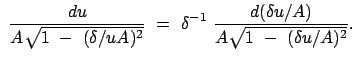
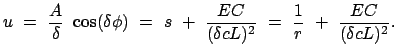
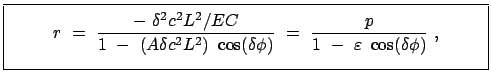
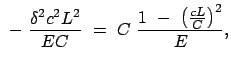
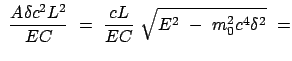
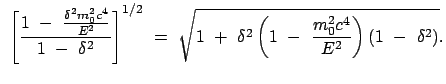
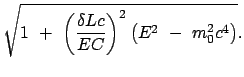
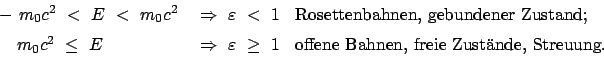
![]() im Argument der cos-Funktion der obigen Bahngleichung verursacht:
im Argument der cos-Funktion der obigen Bahngleichung verursacht:
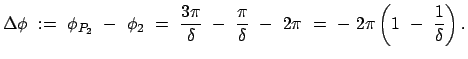
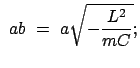
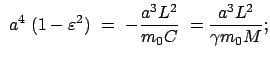
![$\displaystyle \left[a \left(1 - \varepsilon^2\right) \gamma m_0^2 M\right]^{-1} ,
\qquad \frac{T^2}{a^3} = \frac{4 \pi^2}{\gamma M}.$](img2831.gif)
![\includegraphics[width=13cm]{K10A9}](img2836.gif)
![]() (Merkur) und je näher
(Merkur) und je näher
![]() bei 1 liegt (Mars).
bei 1 liegt (Mars).
![]() /Jahrhundert.
Aus den bekannten Störungen (vor allem die Wechselwirkung der Planeten untereinander und
über die Sonne) wurde eine Periheldrehung von 5557.0
/Jahrhundert.
Aus den bekannten Störungen (vor allem die Wechselwirkung der Planeten untereinander und
über die Sonne) wurde eine Periheldrehung von 5557.0![]() /Jahrhundert berechnet.
(Cl. M. Will: Theory and experiment in gravitational physics.
Cambridge University Press 1993).
Die Differenz von 47.7
/Jahrhundert berechnet.
(Cl. M. Will: Theory and experiment in gravitational physics.
Cambridge University Press 1993).
Die Differenz von 47.7![]() /Jahrhundert war schon um 1900 bekannt und
es wurde nach einer Erklärung gesucht.
Gl. (10.77) liefert nur 1/6 dieser Differenz. Aus der
allgemeinen Relativitätstheorie folgt ein Effekt der richtigen Größenordnung
(Einstein, Dicke).
/Jahrhundert war schon um 1900 bekannt und
es wurde nach einer Erklärung gesucht.
Gl. (10.77) liefert nur 1/6 dieser Differenz. Aus der
allgemeinen Relativitätstheorie folgt ein Effekt der richtigen Größenordnung
(Einstein, Dicke).
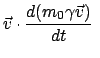
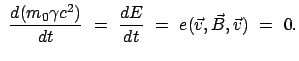

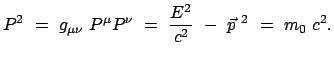
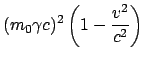
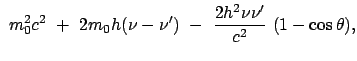
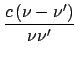
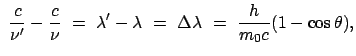
![]() und den numerischen Wert der Comptonwellenlänge
und den numerischen Wert der Comptonwellenlänge ![]() des Elektrons.
des Elektrons.
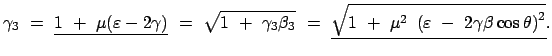
![$\displaystyle = \frac{h\nu}{2} \left[ 1 - \frac{\mu \varepsilon}{2} \
\left(1 - \sqrt{1 - \frac{4}{\varepsilon^2}} \cos\theta\right)^2 \right],$](img2912.gif)
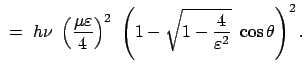
![\includegraphics[scale=0.69]{k10_pion_zerfall_ls_ss}](img2916.gif)
![]() s) und zerfällt hauptsächlich in zwei Gammaquanten:
s) und zerfällt hauptsächlich in zwei Gammaquanten:
![]() und
und ![]() ,
aus (10.94a) der Zusammenhang zwischen dem Winkel
,
aus (10.94a) der Zusammenhang zwischen dem Winkel ![]() und der
Photonenenergie.
und der
Photonenenergie.
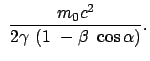
![]() -Quanten, die durch den obigen Zerfall bewirkt wird,
läßt sich ein Wirkungsquerschnitt angeben. Das Pion hat Spin 0 und ist daher sphärisch
symmetrisch; in seinem Eigensystem gibt es keine ausgezeichnete Richtung. Daher muß der
Wirkunsquerschnitt für diese Umwandlung von den Winkeln unabhängig sein:
-Quanten, die durch den obigen Zerfall bewirkt wird,
läßt sich ein Wirkungsquerschnitt angeben. Das Pion hat Spin 0 und ist daher sphärisch
symmetrisch; in seinem Eigensystem gibt es keine ausgezeichnete Richtung. Daher muß der
Wirkunsquerschnitt für diese Umwandlung von den Winkeln unabhängig sein:
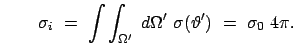
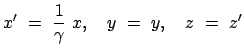
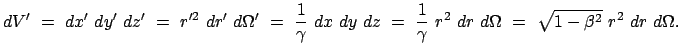
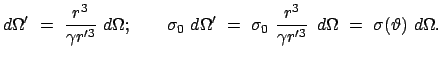
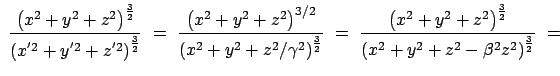
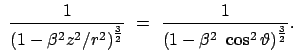
![]() im Laborsystem:
im Laborsystem: