12.1 Mathematische Funktionen

Ziel:

Ein erster Einstieg in MATLAB unter Linux soll geschafft werden. Editieren, Speichern und Ausführen von MATLAB-Skripten. Aufruf einfacher eingebauter Funktionen, Einführung in die Sprachsyntax, einfache graphische Ausgabe.

Vorraussetzung:

Grundlagen von Linux und MATLAB.

Abgabe:

Die Abgabe erfolgt mit Hilfe des Skripts

      uebungsabgabe  filename       % im Terminal
      !uebungsabgabe filename       % in Matlab

Notwendige Abgaben:

uebung1.m und idents.m

12.1.1 Erste Berechnungen

Schreiben Sie im Editor ein MATLAB-Skript uebung1.m, das für Sie die im folgenden beschriebenen Dinge tun soll.

Ein solches MATLAB-Skript sollte mit ein paar Kommentarzeilen beginnen (Name, Übung, Datum). Damit MATLAB weiss, dass es sich nicht um Programmanweisungen handelt, müssen solche Zeilen mit dem Prozentzeichen % beginnen. Füllen Sie also diese Zeilen aus, speichern den File unter dem Namen uebung1.m und geben Sie im MATLAB-Fenster uebung1 ein. Eigentlich sollte gar nichts passieren, da das Programm keine ausführbaren Zeilen enthält.

Probieren Sie jetzt auch mal help uebung1. Was fällt Ihnen auf?

Anmerkung: Das Speichern erfolgt über die Menüeinträge oder mit praktischen Kurzbefehlen. Im emacs speichert C-x C-s, wobei C für das gleichzeitige Drücken der Strg-Taste steht. Im MATLAB-Mode ist auch C-c C-s sehr praktisch. Dieser Befehl speichert das Skript und führt es in MATLAB aus.

Schreiben Sie bei dieser ersten Übung auch folgende Zeilen in das MATLAB-Skript

  clear all            % löscht alle Variablen
  close all            % schließt Graphik-Fenster
  clc                  % löscht den Inhalt des Command-Fensters

Nun kann man mit dem eigentlichen Programmieren beginnen. Weisen Sie den Variablen xstart, xend, xdelta die Werte , , bzw. zu. Erzeugen Sie damit die Vektoren (von xstart bis xend mit der Schrittweite xdelta) und den Vektor . In praktisch allen Programmiersprachen schreibt man für Größen mit Indices (wie hier den Variablenname mit dem Zeichen Unterstrich _ (x_2).

Führen Sie erste Berechnungen aus und geben Sie auf die korrekte Verwendung der Operatoren acht. Denken Sie auch die Verwendung des Strichpunktes am Zeilenende.

$\displaystyle y_1$	$\displaystyle = \sin \pi x$
$\displaystyle y_2$	$\displaystyle = y_1 + x$
$\displaystyle y_3$	$\displaystyle = y_1 x$
$\displaystyle y_4$	$\displaystyle = y_1^2$

Am besten kann man die Ergebnisse mit Hilfe einer graphischen Ausgabe überprüfen. Für den Beginn gibt es hier einmal die Befehlsfolge für eine einfache graphische Ausgabe.

  figure(1);
  plot(x,y_1,x,y_2,x,y_3,x,y_4);
  xlabel('x');
  ylabel('y');
  legend('y_1','y_2','y_3','y_4');
  title('Functions with Sinus');

Die Befehle sollten eigentlich in ihrer einfachen Form selbsterklärend sein. Die vier Kurven

zeichnet dabei der Befehl plot.

Anmerkung: Zeichen zwischen einfachen Hochkommas ' sind Zeichenketten und stellen keine Variablennamen dar (mehr dazu im Laufe der Lehrveranstaltung).

12.1.2 Hyperbelfunktionen

Berechnen Sie in gleicher Weise die Variablen hsin, hcos, htan, hsec mit den Hyperbelfunktion $\sinh x_2$ , $\cosh x_2$ , $\tanh x_2$ und ${\rm sech} \; x_2$ .

Anmerkung: Wenn man eine Varibale z.B. sinh nennt, würde ab diesem Zeitpunkt die Funktion sinh nicht mehr funktionieren, da sie mit eigener Bedeutung überschrieben ist. Daher Vorsicht bei der Wahl der Variablennamen (clear sinh stellt die alte Funktionalität wieder her.

Machen Sie einen ähnlichen Plot wie oben in einem zweiten Graphikfenster, figure(2).

Anmerkung: In Linux können Sie sehr einfach Teile von Bildschirminhalten an anderer Stelle duplizieren. Markieren Sie den zu kopierenden Text mit der linken Maustaste, setzen Sie den Cursor auf die Stelle, wo eingefügt werden soll und drücken Sie die mittlere Maustaste.

12.1.3 Gaussfunktion und Secans Hyperbolicus

Geben Sie den Variablen x_0 und s die Werte 0 und . Berechnen Sie damit die Funktionen

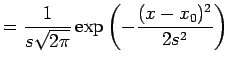$\displaystyle g$	$\displaystyle = \frac{1}{s\sqrt{2\pi}} \exp \left( -\frac{(x-x_0)^2}{2s^2} \right)$
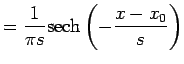$\displaystyle h$	$\displaystyle = \frac{1}{\pi s} {\rm sech} \left( -\frac{x-x_0}{s} \right)$

und stellen Sie sie in einem dritten Graphikfenster dar (sqrt, exp, pi).

12.1.4 Mathematische Identitäten

Schreiben Sie ein MATLAB-Skript idents.m und speichern Sie es in Ihrem MATLAB-Verzeichnis ab. Das Skript soll folgende Dinge tun:

Lesen Sie zwei Zahlen und von der Tastatur ein (input)
Prüfen Sie durch Ausrechnen der linken und rechten Seite der unten angeführten Identitäten die Richtigkeit der Formeln nach. Die Konstante $i = \sqrt{-1}$ steht in MATLAB zur Verfügung, sofern nicht vorher durch eine Anweisung i=... der Wert überschrieben wurde. Verwenden Sie die Variablennamen vl1, vr1, usw. für die Berechnungen.

1 $e^{i a}$ $\cos a + i \sin a$

2 $\log(a b)$ $\log a + \log b$

3 $e^{a+b}$

4 $\cos(a+b)$ $\cos(a)\cos(b) - \sin(a)\sin(b)$

5 $\sin(a+b)$ $\sin(a)\cos(b) + \cos(a)\sin(b)$

6 $\sin(a)$ $\big(e^{i a} - e^{-i a}\big)/(2i)$

7 $\cos(a)$ $\big(e^{i a} + e^{-i a}\big)/2$

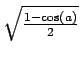8 $\sin(a/2)$ $\sqrt{\frac{1-\cos(a)}{2}}$

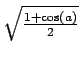9 $\cos(a/2)$ $\sqrt{\frac{1+\cos(a)}{2}}$

Geben Sie dazu das Ergebnis der linken und der rechten Seite der Gleichungen formatiert aus. Eine Einfache Möglichkeit dazu ist
```
     disp([1,vl1,vr1])
     disp([2,vl2,vr2])
```
Anmerkung: Mit Hilfe der eckigen Klammer kann man Zahlen zu Vektoren verbinden, die dann gemeinsam mit disp dargestellt werden können (mehr dazu im Laufe der Lehrveranstaltung).
Anmerkung: Man kann die Gleichheit von zwei Zahlen im Prinzip mit dem Operator == überprüfen. Das führt aber nicht immer zum gewünschten Ergebnis, da bei unterschiedlichen numerischen Berechnungen manchmal Differenzen in den letzten Kommastellen auftreten. Eine alternative Möglichkeit ist daher zu überprüfen, ob die Differenz von 2 Zahlen kleiner als die Zahl eps ist. Die zwei Alternativen können also so geschrieben werden:
```
  l1a = vl1 == vr1;
  l1b = abs(vl1-vr1) < eps;
```
In wenigen Fällen reicht sogar eps noch nicht aus um numerisch die Äquivalenz von zwei Ergebnissen zu zeigen, mit 10*eps ist man aber meist auf der sicheren Seite. Eine bessere Prognose hängt aber von der Größe der zu vergleichenden Zahlen ab. In beiden Fällen bekommt man eine logische Variable (l1a oder l1b), die man ebenfalls ausgeben kann. Logische Variablen haben entweder den Wert 0 (falsch) oder 1 (wahr). Die MATLAB-Hilfe zu Vergleichsoperatoren oder das Kapitel 4.2 liefern nähere Details.

Winfried Kernbichler 2005-04-26

1	$e^{i a}$	$\cos a + i \sin a$
2	$\log(a b)$	$\log a + \log b$
3	$e^{a+b}$
4	$\cos(a+b)$	$\cos(a)\cos(b) - \sin(a)\sin(b)$
5	$\sin(a+b)$	$\sin(a)\cos(b) + \cos(a)\sin(b)$
6	$\sin(a)$	$\big(e^{i a} - e^{-i a}\big)/(2i)$
7	$\cos(a)$	$\big(e^{i a} + e^{-i a}\big)/2$
8	$\sin(a/2)$	$\sqrt{\frac{1-\cos(a)}{2}}$
9	$\cos(a/2)$	$\sqrt{\frac{1+\cos(a)}{2}}$