next up previous contents
Next: 12.3 Spiralen, Schwebung, Gaußverteilung Up: 12. Übungsbeispiele Previous: 12.1 Mathematische Funktionen   Contents

Subsections


12.2 Reguläre Polyeder, Kegelschnitte

Ziel:
Umgang mit Funktionen.

Vorraussetzung:
Grundlagen von Funktionen in MATLAB, wie sie im Kapitel 2 beschrieben werden. Wichtig ist vorallem das Verständnis des Unterschieds zwischen MATLAB-Skripts und MATLAB-Funktionen 2.7.

12.2.1 Reguläre Polyeder

Schreiben Sie eine MATLAB-Funktion regpol.m, die folgende Aufgaben erfüllt. Für eine vorgegebene Kantenlänge $ a$ soll das Volumen $ V$, die Oberfläche $ F$, der Radius der umbeschriebenen Kugel $ R$ und der Radius der einbeschriebenen Kugel $ r$ wahlweise für einen der 5 regulären konvexen Polyeder berechnet werden:

  1. Tetraeder

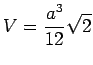      $\displaystyle V = \frac{a^3}{12} \sqrt{2}$ $\displaystyle F = a^2 \sqrt{3}$    
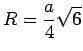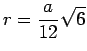      $\displaystyle R = \frac{a}{4} \sqrt{6}$ $\displaystyle r = \frac{a}{12} \sqrt{6}$    

  2. Würfel

      $\displaystyle V = a^3$ $\displaystyle F = 6a^2$    
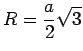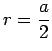      $\displaystyle R = \frac{a}{2} \sqrt{3}$ $\displaystyle r = \frac{a}{2}$    

  3. Oktaeder

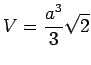      $\displaystyle V = \frac{a^3}{3} \sqrt{2}$ $\displaystyle F = 2a^2 \sqrt{3}$    
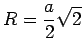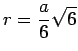      $\displaystyle R = \frac{a}{2} \sqrt{2}$ $\displaystyle r = \frac{a}{6} \sqrt{6}$    

  4. Dodekaeder

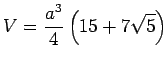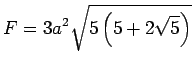      $\displaystyle V = \frac{a^3}{4} \left(15 + 7\sqrt{5}\right)$ $\displaystyle F = 3a^2 \sqrt{5\left(5 + 2\sqrt{5}\right) }$    
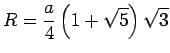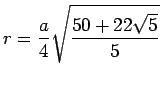      $\displaystyle R = \frac{a}{4} \left( 1 + \sqrt{5} \right) \sqrt{3}$ $\displaystyle r = \frac{a}{4} \sqrt{ \frac{50 + 22\sqrt{5}}{5} }$    

  5. Ikosaeder

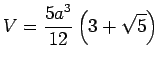      $\displaystyle V = \frac{5a^3}{12} \left(3 + \sqrt{5}\right)$ $\displaystyle F = 5a^2 \sqrt{3}$    
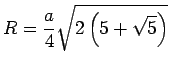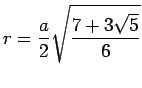      $\displaystyle R = \frac{a}{4} \sqrt{ 2 \left( 5 + \sqrt{5} \right) }$ $\displaystyle r = \frac{a}{2} \sqrt{ \frac{7 + 3\sqrt{5}}{6} }$    

Der Aufruf der Funktion soll folgendermaßen erfolgen: 

  [V,F,R,r] = regpol(typ,a)
Das Programm soll für einen Vektor von $ a$-Werten funktionieren und gleichlange Vektoren mit den Resultaten für $ V$, $ F$, $ R$ und $ r$ zurückgeben. Mit der String-Variablen typ soll der Typ des regulären Polyeders übergeben werden. Im Programm soll zur Unterscheidung der Fälle die switch-Konstruktion verwendet werden: 
  switch lower(typ(1))
     case 't'
        ...
     case 'w'
        ...
     ...
  end
Überlegen Sie, welche Zeichenkette man als typ eingeben kann, was typ(1) bewirkt, und was der Befehl lower dabei bewirkt.

Stellen Sie auch den Unterschied zwischen folgenden Aufrufen der Funktion fest und versuchen Sie das Verhalten zu verstehen. 

  regpol(typ,a)
  V = regpol(typ,a)
  [V,F] = regpol(typ,a)
  [V,F,R] = regpol(typ,a)
  [V,F,R,r] = regpol(typ,a)

12.2.2 Polargleichung von Kegelschnitten

Schreiben Sie eine MATLAB-Funktion kegelpol, welche die Polargleichung von den Kegelschnitten Ellipse, Hyperbel und Parabel in Hauptachsenlage auswertet. Der Aufruf sollte mit 

  r = kegelpol(typ,phi,a,b)
erfolgen, wobei typ der Typ des Kegelschnitts ist, phi ein Vektor von $ \phi$-Werten, und a und b Konstanten zur Beschreibung des Kegelschnittes sind. Diese Werte werden der Funktion vom MATLAB-Skript skegelpol (siehe unten) übergeben. Der Vektor phi ist also ein Übergabeparameter und wird nicht in der Funktion selbst erzeugt. Vergessen Sie nicht die Verwendung der richtigen Operatoren.

Die Formeln für die drei Kegelschnitte lauten:

  1. Ellipse

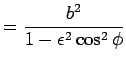    $\displaystyle r^2$ $\displaystyle = \frac{b^2}{1-\epsilon^2 \cos^2 \phi}$    
    $\displaystyle e$ $\displaystyle = \sqrt{a^2-b^2}$    
    $\displaystyle \epsilon$ $\displaystyle = \frac{e}{a}$    
    $\displaystyle a$ $\displaystyle > b$    

  2. Hyperbel

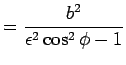    $\displaystyle r^2$ $\displaystyle = \frac{b^2}{\epsilon^2 \cos^2 \phi - 1}$    
    $\displaystyle e$ $\displaystyle = \sqrt{a^2+b^2}$    
    $\displaystyle \epsilon$ $\displaystyle = \frac{e}{a}$    

  3. Parabel

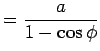    $\displaystyle r$ $\displaystyle = \frac{a}{1 - \cos \phi}$    

Eine Überprüfung aller drei Fälle soll dabei im MATLAB-Skript skegelpol erfolgen, in dem die Werte für a, b und r_0 festgelegt werden. Den $ \phi$-Vektor können Sie mit dem Befehl linspace erzeugen: 
  phi = linspace(phi_min,phi_max,n_points)
Die Winkel für Ellipse, Hyperbel und Parabel reichen dabei von $ \phi_{min}$ bis zum Maximalwert $ \phi_{max}$,

$\displaystyle \phi_{min,max}$ $\displaystyle = 0, \;\; 2\pi$    
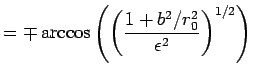$\displaystyle \phi_{min,max}$ $\displaystyle = \mp \arccos \left( \left( \frac{1+b^2/r_0^2}{\epsilon^2} \right)^{1/2} \right)$    
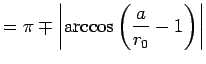$\displaystyle \phi_{min,max}$ $\displaystyle = \pi \mp \left\vert \arccos \left( \frac{a}{r_0} - 1 \right) \right\vert$    

wobei für Hyperbel und Parabel ein größter gewünschter Radius $ r_0>a$ definiert werden muss (warum?). Falls Sie in irgendeinem Fall komplexe Zahlen erhalten, haben Sie mit Sicherheit eine Formel falsch programmiert.

Um zu sehen, ob Sie wirklich eine Ellipse, Hyperbel, bzw. Parabel berechnen, können Sie dabei folgende Plotbefehle ausführen: 

  figure(1) % Ellipse 
  polar(phi,r);

  figure(2) % Hyperbel
  polar(phi,r); hold on; polar(pi-phi,r); hold off;

  figure(3) % Parabel
  polar(phi,r);
Überlegen Sie, warum man in einem Fall zwei Plotbefehle braucht, um den gesamten Kegelschnitt zu zeichnen. Der Befehl hold ermöglicht, dass man zu einer bereits bestehenden Kurve weitere hinzufügt. Man schaltet diesen Modus mit hold on ein und mit hold off aus. Überlegen Sie auch, wie groß man den Wert für n_points setzen muss, damit man vernünftige Kurven erhält.

\includegraphics[width=\graphwidth]{appdata/k_ellipse} \includegraphics[width=\graphwidth]{appdata/k_hyperbel} \includegraphics[width=\graphwidth]{appdata/k_parabel}

next up previous contents
Next: 12.3 Spiralen, Schwebung, Gaußverteilung Up: 12. Übungsbeispiele Previous: 12.1 Mathematische Funktionen   Contents
Winfried Kernbichler 2005-04-26