Unterabschnitte
Zentralkräfte
Die wichtigsten Kräfte in der Natur sind Zentralkräfte, wie z.B. die
Gravitationskraft oder die Coulombkraft. In einem Zentralkraftfeld ist
die Kraft
immer zum Kraftzentrum oder von diesem weg gerichtet. Das Kraftzentrum wird
als Ursprung, 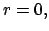 gewählt. Die Stärke der Kraft ist nur eine Funktion
des Abstandes vom Zentrum:
gewählt. Die Stärke der Kraft ist nur eine Funktion
des Abstandes vom Zentrum:
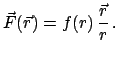 |
(51) |
Wie bereits in §3.5.5 gezeigt worden ist, ist in einem Zentralfeld der
Drehimpulsvektor 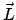 eine Erhaltungsgröße; die Bewegung
verläuft nur in der zu
eine Erhaltungsgröße; die Bewegung
verläuft nur in der zu
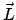 senkrechten Ebene; es existiert ein Potential
und dieses ist sphärisch symmetrisch.
Die Erhaltung der Energie und des Drehimpulses führen zu einer
weitgehenden Reduktion des Problems, sodaß im Prinzip nur mehr
zwei Quadraturen, d.h. zwei unbestimmte Integrale ausgeführt werden
müssen, um
die Bewegung vollständig zu kennen. Diese weitgehende Vereinfachung eines
mechanischen Problems bei Vorliegen einer Zentralkraft ist der Anlaß, daß
man auch bei anderen Kräften manchmal versucht, die nichtzentralen Kräfte
durch eine Zentralkraft zu approximieren (z.B. in der Atomphysik ein
Mehrelektronenproblem durch ein Einelektronenproblem
mit abgeschirmtem Potential).
senkrechten Ebene; es existiert ein Potential
und dieses ist sphärisch symmetrisch.
Die Erhaltung der Energie und des Drehimpulses führen zu einer
weitgehenden Reduktion des Problems, sodaß im Prinzip nur mehr
zwei Quadraturen, d.h. zwei unbestimmte Integrale ausgeführt werden
müssen, um
die Bewegung vollständig zu kennen. Diese weitgehende Vereinfachung eines
mechanischen Problems bei Vorliegen einer Zentralkraft ist der Anlaß, daß
man auch bei anderen Kräften manchmal versucht, die nichtzentralen Kräfte
durch eine Zentralkraft zu approximieren (z.B. in der Atomphysik ein
Mehrelektronenproblem durch ein Einelektronenproblem
mit abgeschirmtem Potential).
Der Fachausdruck ''Zentralkraft'' wird in der Literatur mit zwei nicht
gleichwertigen Bedeutungen verwendet. In der neueren, z.B. Goldstein,
wie auch in diesem
Skriptum, bezeichnet er eine Kraft wie in Gl. (5.1);
dies sichert die Erhaltung von Energie und Drehimpuls.
In der älteren Literatur, z.B. Whittaker, wird jede Kraft, die radial
gerichtet ist,
als Zentralkraft bezeichnet; dann gilt immer noch die Drehimpulserhaltung.
Die Energie ist aber im allgemeinen nicht erhalten; in einem solchen Fall
ist der unten dargelegte Lösungsformalismus nicht anwendbar.
Allgemeine Lösung des Zentralproblems mittels der Erhaltungssätze
Man zentriert das Koordinatensystem im Kraftzentrum 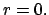 Die
Die 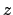 -Achse soll mit dem
Drehimpulsvektor
-Achse soll mit dem
Drehimpulsvektor 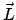 zusammenfallen. In der Bahnebene
(=
zusammenfallen. In der Bahnebene
(= 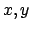 -Ebene) führt man Polarkoordinaten
-Ebene) führt man Polarkoordinaten 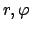 ein:
ein:
Diese führt man in den Energiesatz, Gl. (3.30), ein
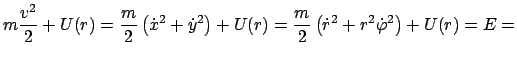 const. const. |
(53) |
und in den Drehimpulssatz, Gl. (3.36)
So erhält man zwei Differentialgleichungen erster Ordnung. Diese kann man im
Prinzip durch Separation lösen. Hierzu wird Gl. (5.4) in
(5.3) eingesetzt und
letztere nach 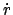 aufgelöst:
aufgelöst:
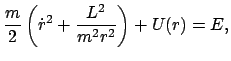 |
(55) |
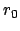 und
und 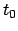 sind Integrationskonstanten, ebenso wie unten
sind Integrationskonstanten, ebenso wie unten
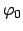 . Gl. (5.6) enthält
das erste Integral, das auszuführen ist. Ist dies getan,
muß man
. Gl. (5.6) enthält
das erste Integral, das auszuführen ist. Ist dies getan,
muß man 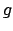 nach
nach  auflösen, den so erhaltenen Ausdruck in Gl. (5.4) einsetzen:
auflösen, den so erhaltenen Ausdruck in Gl. (5.4) einsetzen:
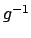 ist der zu
ist der zu 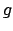 inverse Funktionsoperator. Gl. (5.7) enthält das
zweite Integral, das man benötigt. Hat man es ausgeführt,
dann hat man die Bahn vollständig bestimmt:
Die analytische Auswertung der beiden Integrale (5.6) und (5.7)
und die Inversion
von
inverse Funktionsoperator. Gl. (5.7) enthält das
zweite Integral, das man benötigt. Hat man es ausgeführt,
dann hat man die Bahn vollständig bestimmt:
Die analytische Auswertung der beiden Integrale (5.6) und (5.7)
und die Inversion
von 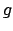 können sehr schwierig oder sogar unmöglich sein. In manchen Fällen
erhält man Integrale, die leichter auszuführen sind, wenn man von der Zeit
können sehr schwierig oder sogar unmöglich sein. In manchen Fällen
erhält man Integrale, die leichter auszuführen sind, wenn man von der Zeit  auf das Azimut
auf das Azimut  als unabhängige Variable übergeht:
als unabhängige Variable übergeht:
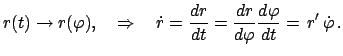 |
(58) |
Die Zeitableitung 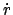 im Energiesatz (5.3) wird gemäß der
Kettenregel in Gl. (5.8)
durch eine Ableitung nach
im Energiesatz (5.3) wird gemäß der
Kettenregel in Gl. (5.8)
durch eine Ableitung nach  ersetzt und
ersetzt und
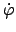 mittels des Drehimpulssatzes (5.4) eliminiert:
mittels des Drehimpulssatzes (5.4) eliminiert:
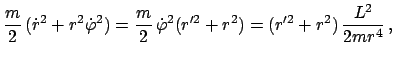 |
|
|
|
![$\displaystyle \frac{L^{2}}{2m} \left[ \frac{r'^{2}}{r^{4}} + \frac{1}{r^{2}} \right]
+ U(r) = E =$](img817.gif) const. const. |
|
|
(59) |
Auch diese Gleichung wird durch Separation gelöst, nachdem man nach 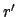 aufgelöst hat.
aufgelöst hat.
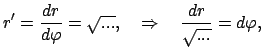 |
|
|
|
![$\displaystyle \varphi - \varphi_{0}
= \int_{r_{0}}^{r} \frac{dr}{\sqrt{\frac{2m[E -U(r)]r^{4}}{L^{2}} - r^{2}}}
: = \hat g(r,r_{0}).$](img820.gif) |
|
|
(510) |
Dieses Integral liefert nach seiner Ausführung die Gestalt der Bahn,
wobei das Azimuth  als Funktion des Abstandes
als Funktion des Abstandes  gegeben ist. Inversion gibt den Abstand
gegeben ist. Inversion gibt den Abstand
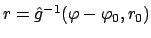 als Funktion von
als Funktion von  .
Dieser Ausdruck wird in den Drehimpulssatz
(5.4) eingesetzt; man separiert, integriert
.
Dieser Ausdruck wird in den Drehimpulssatz
(5.4) eingesetzt; man separiert, integriert
![$\displaystyle \dot \varphi = \frac{d\varphi}{dt} = \frac{L}{mr^{2}}
= \frac{L}{m \left[ \hat g^{-1}(\varphi - \varphi_{0},r_{0}) \right]^{2}},$](img822.gif) |
|
|
|
![$\displaystyle t-t_{0} = \frac{m}{L} \int_{\varphi_{0}}^{\varphi}
d \varphi \lef...
...varphi - \varphi_{0},r_{0}) \right]^{2}
:= \hat h(\varphi - \varphi_{0},r_{0}),$](img823.gif) |
|
|
(511) |
invertiert und hat die Bahn:
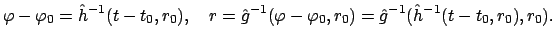
Die analytische Durchführung der oben angeführten Operationen ist zum Teil
schwierig, zum Teil überhaupt nicht möglich. Das Integral (5.10)
kann für den
harmonischen Oszillator (Potential
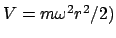 , das
Keplerproblem
, das
Keplerproblem 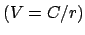 und das Potential
und das Potential
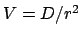 mit elementaren Funktionen ausgeführt werden. Das Integral (5.11)
kann beim
Keplerproblem ausgeführt, der resultierende Ausdruck aber nicht mehr analytisch
invertiert werden. Für ungefähr 18 andere Zentralpotentiale kann das Integral
(5.10) mittels elliptischer Integrale ausgeführt werden.
(Goldstein [1], S. 80 - 86). Das Theorem von Newton
(K8. Ü5) ermöglicht es, die bekannte Lösung für ein Kraftfeld
mit elementaren Funktionen ausgeführt werden. Das Integral (5.11)
kann beim
Keplerproblem ausgeführt, der resultierende Ausdruck aber nicht mehr analytisch
invertiert werden. Für ungefähr 18 andere Zentralpotentiale kann das Integral
(5.10) mittels elliptischer Integrale ausgeführt werden.
(Goldstein [1], S. 80 - 86). Das Theorem von Newton
(K8. Ü5) ermöglicht es, die bekannte Lösung für ein Kraftfeld 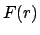 zu
benutzen, um auch den Fall zu lösen, wo zu
zu
benutzen, um auch den Fall zu lösen, wo zu 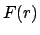 noch eine zusätzliche
Kraft
noch eine zusätzliche
Kraft 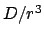 hinzukommt. Die numerische Auswertung der Integrale und der
Inversionen bereitet auf einem Computer keine besonderen Probleme, wenn man
beachtet, daß die Wurzel im Nenner an den Umkehrpunkten Null, das Integral
also schwach singulär wird. Zweckmässiger ist es aber, die Newtonschen
Bewegungsgleichungen in rechtwinkligen Koordinaten direkt durch numerische
Integration (z.B. Runge-Kutta Verfahren, NDSolve[...] in Mathematica) zu
lösen.
hinzukommt. Die numerische Auswertung der Integrale und der
Inversionen bereitet auf einem Computer keine besonderen Probleme, wenn man
beachtet, daß die Wurzel im Nenner an den Umkehrpunkten Null, das Integral
also schwach singulär wird. Zweckmässiger ist es aber, die Newtonschen
Bewegungsgleichungen in rechtwinkligen Koordinaten direkt durch numerische
Integration (z.B. Runge-Kutta Verfahren, NDSolve[...] in Mathematica) zu
lösen.
Wichtige Aussagen über die Bahn können bereits aus dem Energiesatz abgeleitet
werden. Wir setzen 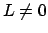 voraus. Gl. (5.5) wird umgeschrieben:
voraus. Gl. (5.5) wird umgeschrieben:
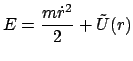 mit mit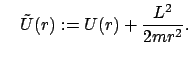 |
(512) |
Der Fliehkraftterm
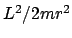 sieht auch wie ein Potential aus,
er wird daher mit
dem wahren Potential
sieht auch wie ein Potential aus,
er wird daher mit
dem wahren Potential 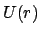 zum sogenannten Pseudo- oder Scheinpotential
zum sogenannten Pseudo- oder Scheinpotential
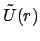 vereinigt. Aus (5.12) folgt nun:
vereinigt. Aus (5.12) folgt nun:
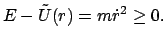 |
(513) |
Das Gleichheitszeichen gibt die Umkehrpunkte der Bahn; an ihnen hat der Abstand
vom Zentrum maximalen oder minimalen Wert:
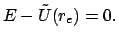 |
(514) |
Abbildung:
Allgemeine Aussagen über Bahnen abgeleitet aus dem Pseudopotential
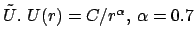 . Bahn berechnet
mittels numerischer Integration der Bewegungsgleichungen in Mathematica.
. Bahn berechnet
mittels numerischer Integration der Bewegungsgleichungen in Mathematica.
|
![\includegraphics[scale=0.9]{k5_zentralpot}](img838.gif) |
Dies ist eine algebraische oder transzendente Gleichung zur Berechnung der
maximalen und minimalen Bahnradien. Gl. (5.13) gibt Auskunft über
den zulässigen Bereich des Radius  . Wir setzen nun voraus,
daß das Potential anziehend
ist und ein definiertes Verhalten an den Grenzen hat:
Die letzte Bedingung bewirkt, daß für kleine
. Wir setzen nun voraus,
daß das Potential anziehend
ist und ein definiertes Verhalten an den Grenzen hat:
Die letzte Bedingung bewirkt, daß für kleine  der Fliehkraftterm
dominiert und eine Annäherung bis an
der Fliehkraftterm
dominiert und eine Annäherung bis an 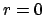 verhindert.
Die Diskussion der Gl. (5.13) kann dann in graphischer Form erfolgen
(s.Abb. 5.1).
Das Zusammenwirken des abstoßenden Fliehkraftpotentials
verhindert.
Die Diskussion der Gl. (5.13) kann dann in graphischer Form erfolgen
(s.Abb. 5.1).
Das Zusammenwirken des abstoßenden Fliehkraftpotentials
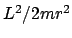 und des anziehenden Potentials
und des anziehenden Potentials 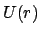 geben dem
Pseudopotential
geben dem
Pseudopotential
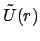 das Aussehen einer Potentialmulde.
Für Energiewerte
das Aussehen einer Potentialmulde.
Für Energiewerte 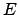 mit
mit
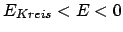 ist das Teilchen
in der Potentialmulde
zwischen dem (von der Energie
ist das Teilchen
in der Potentialmulde
zwischen dem (von der Energie 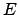 abhängigen) Minimal-, Maximalwert
abhängigen) Minimal-, Maximalwert
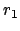 bzw.
bzw. 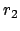 eingesperrt. Die zugehörige Rosettenbahn
erhält man natürlich erst durch (analytische oder numerische)
Integration der Gl. (5.10) oder der Newtonschen Bewegungsgleichungen.
Dem kleinstmöglichen Energiewert
eingesperrt. Die zugehörige Rosettenbahn
erhält man natürlich erst durch (analytische oder numerische)
Integration der Gl. (5.10) oder der Newtonschen Bewegungsgleichungen.
Dem kleinstmöglichen Energiewert
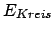 entspricht eine Kreisbahn
entspricht eine Kreisbahn 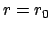 . Für
. Für 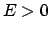 wird
das Teilchen gestreut. Es kann sich dem
Kraftzentrum nur bis zu
wird
das Teilchen gestreut. Es kann sich dem
Kraftzentrum nur bis zu 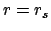 nähern.
Bertrand hat bewiesen, daß für die erwähnten Potentiale
nähern.
Bertrand hat bewiesen, daß für die erwähnten Potentiale 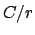 und
und 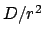 alle endlichen Bahnen geschlossen (und Ellipsen) sind
(s. a. Landau, Lifschitz [2], §2.5.4).
alle endlichen Bahnen geschlossen (und Ellipsen) sind
(s. a. Landau, Lifschitz [2], §2.5.4).
Die Keplerbewegung
Bei der Keplerbewegung bewegt sich ein Massenpunkt unter dem Einfluß der
Gravitations- oder Coulombkraft:
Abbildung 5.2:
Kepler- und Coulombproblem
|
![\includegraphics[scale=1]{k5_keplercoulomb}](img854.gif) |
deren Betrag
dem reziproken Quadrat des Abstandes vom Zentrum proportional ist. Die
Newtonsche Gravitationskraft wirkt zwischen zwei Massen 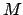 und
und  ,
die Coulombsche Kraft zwischen zwei Ladungen
,
die Coulombsche Kraft zwischen zwei Ladungen 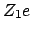 und
und 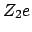 (
(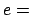 Elementarladung
Elementarladung
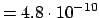 cgs-Einh., bzw.
cgs-Einh., bzw.
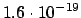 Cb).
Cb).
Einer der beiden Körper (im Falle der Planetenbewegung die Sonne,
im Atom der Kern) ist sehr viel schwerer als der andere, sodaß
dieser in guter Näherung als im Zentrum fixiert betrachtet werden kann;
er erzeugt das
Kraftfeld, in dem sich der leichtere (der Planet, das Elektron, das
Alphateilchen bei der Rutherfordstreuung) bewegt (s. Abb. 5.2).
Der Drehimpuls
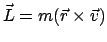 ist konstant, da
ist konstant, da
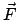 Zentralkraft ist. Die Lösungen unterscheiden sich etwas,
je nachdem, ob
Zentralkraft ist. Die Lösungen unterscheiden sich etwas,
je nachdem, ob 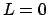 oder
oder 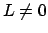 ist.
ist.
Aus Gl. (5.12) wird:
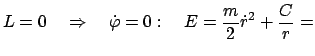 const. const.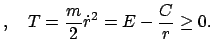 |
(516) |
Die Bewegungsmöglichkeiten ergeben sich aus dem Energiesatz
(5.16): Die kinetische Energie darf nicht negativ sein,
also auch nicht die rechte Seite der
obigen Gleichung. Dies wird graphisch gezeigt.
1. Anziehung: 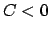 , z.B. Kern und Elektron, Massenanziehung
(s. Abb. 5.3).
1.1
, z.B. Kern und Elektron, Massenanziehung
(s. Abb. 5.3).
1.1 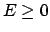 : Hier ist die rechte Seite der
obigen Gleichung immer positiv,
die Bewegung ist keiner Beschränkung unterworfen:
: Hier ist die rechte Seite der
obigen Gleichung immer positiv,
die Bewegung ist keiner Beschränkung unterworfen:
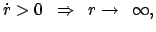
oder
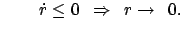
1.2 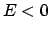 : Hier ist die rechte Seite der
obigen Gleichung nur im Bereich
: Hier ist die rechte Seite der
obigen Gleichung nur im Bereich
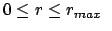 positiv, die Bewegung kann nur in diesem Intervall
stattfinden: gebundener Zustand. Umkehrpunkt bei:
2. Abstoßung,
positiv, die Bewegung kann nur in diesem Intervall
stattfinden: gebundener Zustand. Umkehrpunkt bei:
2. Abstoßung, 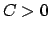 , gleichnamige Ladungen (s.Abb. 5.4).
Aus dem Energiesatz (5.16) folgt,
daß nur
, gleichnamige Ladungen (s.Abb. 5.4).
Aus dem Energiesatz (5.16) folgt,
daß nur 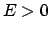 möglich ist. Die rechte Seite obiger Gleichung ist positiv
für
möglich ist. Die rechte Seite obiger Gleichung ist positiv
für
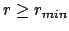 . Umkehrpunkt:
. Umkehrpunkt:
Abbildung:
Bewegungsmöglichkeiten (gefärbter Bereich) bei Anziehung.
(a) Negative Gesamtenergie, (b) positive Gesamtenergie
|
[]
![\includegraphics[scale=0.84]{k5_bewegmog_a}](img874.gif) []
[]
![\includegraphics[scale=0.86]{k5_bewegmog_b}](img875.gif) |
Abbildung:
Bewegungsmöglichkeit (gefärbter Bereich) bei Abstoßung
|
![\includegraphics[scale=0.87]{k5_bewmog_abst}](img876.gif) |
Aus Gl. (5.5) folgt für das Coulombpotential 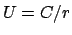 :
:
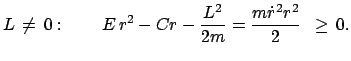 |
(517) |
Für das Gleichheitszeichen in dieser Gleichung ergeben sich die
Umkehrpunkte
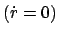 :
:
a) E = 0: reelle Werte für 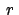 nur bei
nur bei 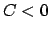 (Anziehung) möglich.
(Anziehung) möglich.
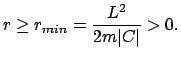 |
(518) |
b) E 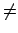 0:
0:
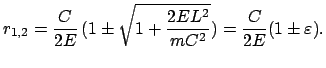 |
(519) |
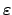 ist hier eine Abkürzung für die Wurzel; unten wird
sich zeigen, daß es
die numerische Exzentrizität ist. Aus (5.18) und (5.19)
ergeben
sich die Umkehrpunkte (nur reelle Werte sind brauchbar), aus (5.17)
der Variationsbereich von
ist hier eine Abkürzung für die Wurzel; unten wird
sich zeigen, daß es
die numerische Exzentrizität ist. Aus (5.18) und (5.19)
ergeben
sich die Umkehrpunkte (nur reelle Werte sind brauchbar), aus (5.17)
der Variationsbereich von  :
:
![\begin{displaymath}\begin{array}{lccccclcl} 1. & C < 0: & & & & & & & [1mm] 1...
...psilon)\frac{C}{2E} &=& r_{min} \leq r \leq \infty. \end{array}\end{displaymath}](img885.gif) |
(520) |
Wir berechnen die Bahnkurve nicht, indem wir die Integrale des §
5.1 ausführen,
sondern wir geben 5 Integrale der Bewegung an und leiten daraus die Bahnkurve
ab (vgl. Satz 1 von §3.5.6). Neben dem Drehimpuls 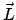 und der
Gesamtenergie
und der
Gesamtenergie 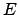 ist der Laplace-Lenzsche Vektor :
ist der Laplace-Lenzsche Vektor :
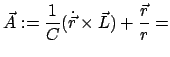 const. const. |
(521) |
ein spezifisches Integral der Bewegung des Kraftfeldes (5.15). Dies
beweist man,
indem man die Bewegungsgleichung vektoriell mit dem Drehimpulsvektor 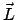 multipliziert:
multipliziert:
Daraus folgt Gl. (5.21). Von den 7 Grössen
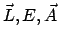 sind nur 5
unabhängig, weil
sie durch 2 Relationen miteinander verknüpft sind. Die erste:
ergibt sich durch einfaches Ausrechnen. Die zweite ergibt sich durch
Quadrieren der Gl. (5.21) und Anwendung der Vektorrelationen:
Die verbleibenden 5 unabhängigen Konstanten der Bewegung müssen gemäß
Satz 1, §3.5.6, zur Bestimmung der Bahn
genügen. Dazu bilden wir das innere
Produkt des Radiusvektors
sind nur 5
unabhängig, weil
sie durch 2 Relationen miteinander verknüpft sind. Die erste:
ergibt sich durch einfaches Ausrechnen. Die zweite ergibt sich durch
Quadrieren der Gl. (5.21) und Anwendung der Vektorrelationen:
Die verbleibenden 5 unabhängigen Konstanten der Bewegung müssen gemäß
Satz 1, §3.5.6, zur Bestimmung der Bahn
genügen. Dazu bilden wir das innere
Produkt des Radiusvektors 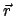 mit dem Vektor
mit dem Vektor 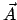 , Gl. (5.21), und
lösen die unterstrichenen Teile der erhaltenen Gleichung nach
, Gl. (5.21), und
lösen die unterstrichenen Teile der erhaltenen Gleichung nach  auf:
auf:
Die unterstrichenen Terme geben die folgende Gleichung:
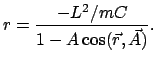 |
(522) |
Dieses Resultat wird mit der Formel für Kegelschnitte in Polarkoordinaten
verglichen.
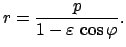 |
(523) |
Hier bezeichnet 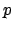 den Parameter; dieser hat mit dem Impuls (auch oft
mit
den Parameter; dieser hat mit dem Impuls (auch oft
mit 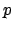 bezeichnet) nichts zu tun.
Der Betrag des Vektors
bezeichnet) nichts zu tun.
Der Betrag des Vektors 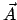 ist gleich der numerischen Exzentrizität
ist gleich der numerischen Exzentrizität
 |
(524) |
Der Vektor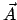 liegt in der Apsidenlinie, das ist jene Gerade, die
vom sonnennächsten Punkt der Bahn (Perihel, Perizentrum) durch das
Kraftzentrum,
liegt in der Apsidenlinie, das ist jene Gerade, die
vom sonnennächsten Punkt der Bahn (Perihel, Perizentrum) durch das
Kraftzentrum, 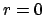 ,
läuft.
,
läuft. 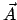 gibt daher die Lage des Perihels und der
gibt daher die Lage des Perihels und der 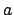 -Achse des
Kegelschnitts an. Dies ersieht man aus (5.22):
-Achse des
Kegelschnitts an. Dies ersieht man aus (5.22):  nimmt seine Extrema (dies entspricht den Perizentren und dem Apozentrum)
für
nimmt seine Extrema (dies entspricht den Perizentren und dem Apozentrum)
für
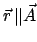 an.
an. 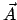 weist vom Perihel weg für
weist vom Perihel weg für 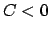 (Anziehung, Abb. 5.5(a)), zum
Perihel für
(Anziehung, Abb. 5.5(a)), zum
Perihel für 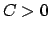 (Abstoßung, Abb. 5.5(b)); Tabelle (5.20) zeigt: bei
(Abstoßung, Abb. 5.5(b)); Tabelle (5.20) zeigt: bei 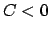 ist
ist
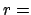 Min. für
Min. für
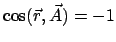 ; für
; für 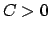 ist
ist
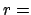 Min. für
Min. für
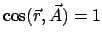 .
.
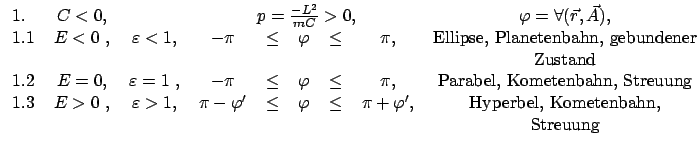 |
(525) |
In dieser Tabelle und den folgenden Formeln sind 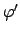 und
und 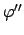 folgende Abkürzungen:
folgende Abkürzungen:
Bei Abstoßung (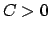 ) durchläuft der geladene Massenpunkt den anderen
Zweig der Hyperbel. In Polarkoordinaten lautet dessen Gleichung:
) durchläuft der geladene Massenpunkt den anderen
Zweig der Hyperbel. In Polarkoordinaten lautet dessen Gleichung:
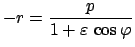 |
(526) |
Das negative Vorzeichen vor  bedeutet, daß der radiale Strahl in
entgegegesetzter Richtung zu verfolgen ist
(s. Abb. 5.5(b)). Dann ergibt sich
durch Vergleich obiger Gleichung mit Gl. (5.22):
bedeutet, daß der radiale Strahl in
entgegegesetzter Richtung zu verfolgen ist
(s. Abb. 5.5(b)). Dann ergibt sich
durch Vergleich obiger Gleichung mit Gl. (5.22):
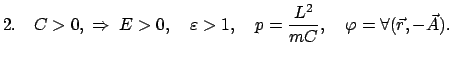 |
(527) |
Der Variationsbereich des Winkels  ist dabei:
ist dabei:
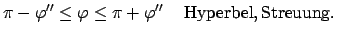 |
(528) |
Keplersche Gesetze
Aus obiger Lösung lassen sich die drei Keplerschen Gesetze der
Planetenbewegung ableiten, die J. Kepler empirisch aus Tycho Brahe's
Sternbeobachtungen gefunden hat.
- Die Bahnen im Kraftfeld der Sonne (des Kernes) sind Kegelschnitte,
in deren
einem Brennpunkt die Sonne (der Kern) sitzt. Dies folgt aus
Gl. (5.22).
- Der Flächensatz: Der Fahrstrahl von der Sonne zum Planeten überstreicht
in gleichen Zeiten gleiche Flächen. Dies gilt in jedem Zentralkraftfeld
und folgt aus dem Drehimpulssatz, s. (3.41).
- Für die Umlaufzeiten geschlossener Bahnen (Ellipsen) und deren große
Halbachsen
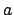 gilt für alle Planeten
gilt für alle Planeten
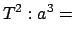
const.
Beweis: Aus Gl. (5.23 ) erhält man:
Man verwendet den Flächensatz, Gl. (3.41), für einen ganzen Umlauf
(
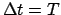 ),
d.h. für die ganze Ellipse (Fläche =
),
d.h. für die ganze Ellipse (Fläche = 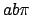 ):
):
Das Verhältnis 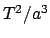 hängt nur von der Gravitationskonstante
hängt nur von der Gravitationskonstante
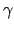 und der
Zentralmasse
und der
Zentralmasse 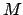 ab, nicht aber von den Daten der Planeten.
ab, nicht aber von den Daten der Planeten.
Rutherfordstreuung
Ein Teilchen (Projektil, Streuteilchen) (Masse  , Ladungszahl
, Ladungszahl 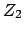 )
wird an einem fixen Targetteilchen (mit Ladung
)
wird an einem fixen Targetteilchen (mit Ladung 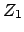 )
gestreut;
)
gestreut;
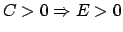 ; doch gilt das Resultat auch für
; doch gilt das Resultat auch für 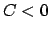 ,
wenn
,
wenn 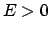 ist.
ist.
Die Berechnungen des vorgehenden Abschnittes erfolgten unter der Annahme, daß
das streuende Teilchen fix ist; sie sind also nur verwendbar, wenn die Masse
des Streukerns groß ist (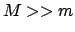 ). Das Streuteilchen kommt mit
Geschwindigkeit
). Das Streuteilchen kommt mit
Geschwindigkeit 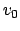 aus dem Unendlichen. Würde es keine Ablenkung
erfahren, dann wäre
seine Bahn eine Gerade, die vom Kern den Normalabstand
aus dem Unendlichen. Würde es keine Ablenkung
erfahren, dann wäre
seine Bahn eine Gerade, die vom Kern den Normalabstand 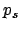 hätte;
deshalb
heißt
hätte;
deshalb
heißt 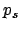 der Stoßparameter. Aufgrund seiner Ladung wird
das Streuteilchen abgelenkt, es wird um den Winkel
der Stoßparameter. Aufgrund seiner Ladung wird
das Streuteilchen abgelenkt, es wird um den Winkel  gestreut
(Abb. 5.5).
gestreut
(Abb. 5.5).
.
Gesamtenergie 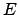 und Drehimpuls
und Drehimpuls 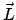 werden aus den Anfangsdaten im
Unendlichen bestimmt:
Einsetzen der Resultate dieser beiden Zeilen in die obige Formel für den
Streuwinkel gibt mit
werden aus den Anfangsdaten im
Unendlichen bestimmt:
Einsetzen der Resultate dieser beiden Zeilen in die obige Formel für den
Streuwinkel gibt mit
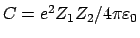 den folgenden
Zusammenhang zwischen dem Streuwinkel
den folgenden
Zusammenhang zwischen dem Streuwinkel
 und dem Stoßparamter
und dem Stoßparamter 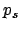 :
:
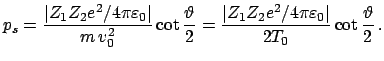 |
(529) |
Rutherford verwendete für seine Streuexperimente 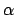 -Teilchen
(Masse
-Teilchen
(Masse
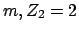 ), die von einem radioaktiven Kern (Thorium C)
mit der kinetischen Energie
), die von einem radioaktiven Kern (Thorium C)
mit der kinetischen Energie 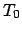 emittiert werden. Damit wird
aus obiger Formel:
emittiert werden. Damit wird
aus obiger Formel:
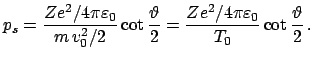 |
(530) |
Der Satz von Gauß besagt:
Die Kraft auf eine Punktmasse  (bzw. Punktladung
(bzw. Punktladung 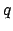 ) im Innern einer
homogen mit Masse (Ladung) belegten Kugelschale ist Null.
) im Innern einer
homogen mit Masse (Ladung) belegten Kugelschale ist Null.
Im nachfolgenden Beweis sieht man, daß der Satz nur gilt für Kräfte,
die ein Abstandsverhalten wie 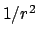 haben.
haben.
Beweis: Die Massendichte auf der Kugelschale ist:
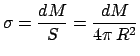 |
(531) |
(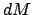 = Gesamtmasse,
= Gesamtmasse,  = Oberfläche der Kugelschale.)
Die Beträge der Kräfte
= Oberfläche der Kugelschale.)
Die Beträge der Kräfte
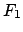 bzw.
bzw. 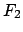 der Oberflächenelemente
der Oberflächenelemente 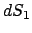 bzw.
bzw. 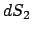 auf
auf  sind nach dem Newtonschen Attraktionsgesetz (5.15):
sind nach dem Newtonschen Attraktionsgesetz (5.15):
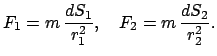 |
(532) |
Die einander gegenüberliegenden Oberflächenelemente
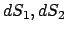 werden durch
den beiderseits gleich großen Raumwinkel
werden durch
den beiderseits gleich großen Raumwinkel 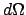 ausgedrückt
(Abb. 5.6(a)):
ausgedrückt
(Abb. 5.6(a)):
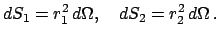 |
(533) |
Damit wird
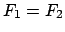 ! Die Kräfte haben entgegengesetzte Richtung,
ihre Resultierende ist Null, daher auch das Integral über
die ganze Kugeloberfläche.
Das gleiche Resultat erhält man auch für eine homogene elektrische
Oberflächenladung mittels des Coulombschen Gesetzes.
! Die Kräfte haben entgegengesetzte Richtung,
ihre Resultierende ist Null, daher auch das Integral über
die ganze Kugeloberfläche.
Das gleiche Resultat erhält man auch für eine homogene elektrische
Oberflächenladung mittels des Coulombschen Gesetzes.
Abbildung:
a) Oberflächenelemente und Raumwinkel.
b) Integration über die Kugelschale
|
[]
![\includegraphics[scale=0.84]{k5_oberfl_raumw}](img941.gif) []
[]
![\includegraphics[scale=0.86]{k5_kugelschale}](img942.gif) |
Die Kraft auf die Punktmasse  , die von der auf der Schale homogen
verteilten Masse
, die von der auf der Schale homogen
verteilten Masse 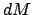 ausgeübt wird, ist identisch mit der Kraft, die
bei Abwesenheit der Flächenbelegung
ausgeübt wird, ist identisch mit der Kraft, die
bei Abwesenheit der Flächenbelegung 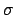 eine Punktmasse
eine Punktmasse 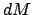 ausübt,
die im Mittelpunkt der Schale angebracht ist. Dazu wird gezeigt, daß das
Potential einer Masse
ausübt,
die im Mittelpunkt der Schale angebracht ist. Dazu wird gezeigt, daß das
Potential einer Masse 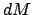 (einer Ladung
(einer Ladung 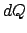 ), die über eine
Kugelschale
), die über eine
Kugelschale  vom Radius
vom Radius 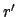 homogen verteilt ist, Gl. (5.31),
dasselbe ist wie das einer Punktmasse
homogen verteilt ist, Gl. (5.31),
dasselbe ist wie das einer Punktmasse 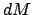 (einer Punktladung
(einer Punktladung 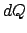 ),
die sich im Mittelpunkt
),
die sich im Mittelpunkt 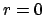 der Kugelschale
der Kugelschale  befindet. Zunächst
wird das Potential
befindet. Zunächst
wird das Potential 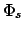 im Punkt
im Punkt 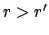 , das von einer
mit der Massendichte
, das von einer
mit der Massendichte 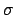 belegten Kugelzone
erzeugt wird, berechnet (Abb. 5.6(b)):
belegten Kugelzone
erzeugt wird, berechnet (Abb. 5.6(b)):
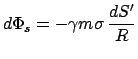 |
(534) |
mit
und (Kosinussatz, s.Abb. 5.6b)
Integration über die ganze Kugelschale gibt das nachfolgend
angegebene Potential 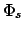 . Zur Ausführung der Integration
wird
. Zur Ausführung der Integration
wird 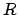 als neue Integrationsvariable eingeführt.
als neue Integrationsvariable eingeführt.
Im Inneren der Schale vom Radius 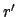 ist die Kraft Null, daher das
Potential konstant. Diese Konstante wird so gewählt, daß die
potentielle Energie stetig ist :
ist die Kraft Null, daher das
Potential konstant. Diese Konstante wird so gewählt, daß die
potentielle Energie stetig ist :
Für die Kraft auf die Punktmasse  gilt gemäß dem vorher
Gesagten:
gilt gemäß dem vorher
Gesagten:
Für eine Punktladung 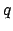 im Äußeren bzw. Inneren einer Schale vom
Radius
im Äußeren bzw. Inneren einer Schale vom
Radius 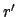 , auf der eine Ladung
, auf der eine Ladung 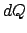 homogen verschmiert ist, muß
in Gln. (5.36) und (5.37)
homogen verschmiert ist, muß
in Gln. (5.36) und (5.37)
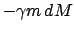 ersetzt werden durch
ersetzt werden durch 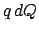 (cgs-Einheiten) bzw.
(cgs-Einheiten) bzw.
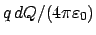 (MKSA-Einheiten).
(MKSA-Einheiten).
Dieser Sachverhalt führt zu einer großen Vereinfachung der Behandlung der
Bewegung von Punktmassen (oder Punktladungen) im Inneren von
radialsymmetrischen
Massen- (oder Ladungsverteilungen). Denn aus dem Gaußschen Satz folgt:
Befindet sich eine Punktmasse  (Punktladung
(Punktladung 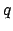 ) im Inneren
einer radialsymmetrischen Massen-(Ladungs-)verteilung im Abstand
) im Inneren
einer radialsymmetrischen Massen-(Ladungs-)verteilung im Abstand  vom Symmetriezentrum, dann übt der außerhalb
vom Symmetriezentrum, dann übt der außerhalb  gelegene Anteil der
Verteilung keine
Kraft auf
gelegene Anteil der
Verteilung keine
Kraft auf  (
(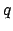 ) aus. Daher wirkt auf
) aus. Daher wirkt auf  (
(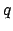 ) nur der innerhalb
von
) nur der innerhalb
von  gelegene Anteil der Massen-(Ladungs-)verteilung; dieser kann
so berücksichtigt werden als wenn er im Symmetriezentrum
angebracht wäre. Bei der Berechnung des Potentials muß aber
darauf geachtet werden, daß der außerhalb
gelegene Anteil der Massen-(Ladungs-)verteilung; dieser kann
so berücksichtigt werden als wenn er im Symmetriezentrum
angebracht wäre. Bei der Berechnung des Potentials muß aber
darauf geachtet werden, daß der außerhalb  liegende Anteil der
Massenverteilung einen Beitrag zum Potential liefert. Mit diesen
Überlegungen läßt sich die potentielle Energie einer Punktmasse
liegende Anteil der
Massenverteilung einen Beitrag zum Potential liefert. Mit diesen
Überlegungen läßt sich die potentielle Energie einer Punktmasse  (einer Punktladung
(einer Punktladung 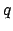 ) im Inneren und Äußeren einer sphärischen
Massenverteilung
) im Inneren und Äußeren einer sphärischen
Massenverteilung 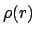 berechnen. Die Gesamtmasse
berechnen. Die Gesamtmasse 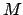 beträgt:
beträgt:
Die Massendichte 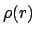 muß für
muß für
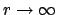 hinreichend stark verschwinden,
damit das obige Integral existiert. Ist die Massendichte nur in einem
endlichen Raumgebiet von Null verschieden, z.B.
dann ist im Äußeren die potentielle Energie der Punktmasse
hinreichend stark verschwinden,
damit das obige Integral existiert. Ist die Massendichte nur in einem
endlichen Raumgebiet von Null verschieden, z.B.
dann ist im Äußeren die potentielle Energie der Punktmasse  gegeben
durch:
gegeben
durch:
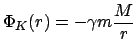 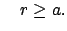 |
(538) |
Befindet sich  im Inneren der Massenverteilung, und zwar im Abstand
im Inneren der Massenverteilung, und zwar im Abstand
 vom Zentrum
vom Zentrum 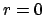 der sphärischen Verteilung, dann müssen
die Beiträge, die vom inneren Anteil
der sphärischen Verteilung, dann müssen
die Beiträge, die vom inneren Anteil 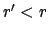 und vom äußeren
Anteil
und vom äußeren
Anteil 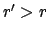 der Massendichte stammen, wegen Gl. (5.36) gesondert
behandelt werden:
der Massendichte stammen, wegen Gl. (5.36) gesondert
behandelt werden:
Die beiden Integrale der vorletzten Zeile wurden in der letzten zu einem
zusammengefaßt unter Einführung der Greenschen Funktion
 heißt die Aufpunktskoordinate; sie bezeichnet den Ort, an dem sich
die Punktmasse
heißt die Aufpunktskoordinate; sie bezeichnet den Ort, an dem sich
die Punktmasse  befindet.
befindet. 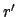 ist die Quellpunktskoordinate;
sie gibt die Lage des Volumselements der Quellverteilung (hier einer
Kugelschale der Dicke
ist die Quellpunktskoordinate;
sie gibt die Lage des Volumselements der Quellverteilung (hier einer
Kugelschale der Dicke 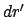 ) an; über sie wird integriert, um die Beiträge
der gesamten Massenverteilung in ihrer Wirkung auf
) an; über sie wird integriert, um die Beiträge
der gesamten Massenverteilung in ihrer Wirkung auf  zu erfassen.
Die Greensche Funktion wird durch zwei verschiedene
Funktionsoperatoren beschrieben, ist aber stetig. Gleichungen
(5.39) und (5.40) gelten auch für
zu erfassen.
Die Greensche Funktion wird durch zwei verschiedene
Funktionsoperatoren beschrieben, ist aber stetig. Gleichungen
(5.39) und (5.40) gelten auch für 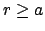 und
liefern dann als Resultat Gl. (5.38).
und
liefern dann als Resultat Gl. (5.38).
Für eine sphärische Ladungsverteilung 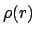 ist in den obigen
Formeln
ist in den obigen
Formeln
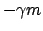 durch die Ladung
durch die Ladung 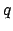 (cgs-Einheiten) bzw.
(cgs-Einheiten) bzw.
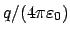 (MKSA-Einheiten) zu ersetzen.
(MKSA-Einheiten) zu ersetzen.
Obige Formeln (5.39) und(5.40) gelten nur für sphärisch
symmetrische Massen- oder Ladungsverteilungen. Der Vollständigkeit halber
werden - ohne Beweis - die zu den eben genannten entsprechenden Formeln für
den allgemeinen Fall angegeben. In diesem ist eine Massen- oder Ladungsverteilung
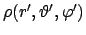 gegeben. Die Gesamtmasse
gegeben. Die Gesamtmasse 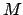 (analog dazu die Gesamtladung
(analog dazu die Gesamtladung 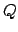 )
ist durch das folgende Integral definiert:
)
ist durch das folgende Integral definiert:
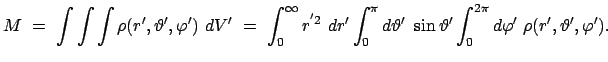
Das Potential an einem Punkt mit den sphärischen Koordinaten
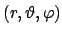 ist dann gegeben durch
ist dann gegeben durch
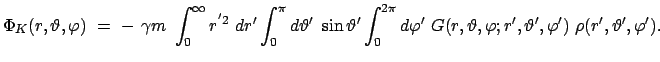
Die zugehörige Greensche Funktion
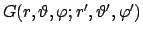 ist gegeben durch:
ist gegeben durch:
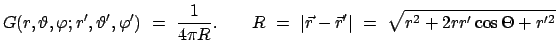
ist der Abstand zwischen dem Aufpunkt 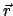 und dem Quellpunkt
und dem Quellpunkt
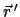 .
Er hängt auch von
.
Er hängt auch von  ,
,  ,
,
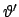 und
und 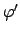 ab, weil der Raumwinkel
ab, weil der Raumwinkel 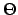 zwischen diesen beiden Vektoren von diesen Variablen abhängt:
zwischen diesen beiden Vektoren von diesen Variablen abhängt:
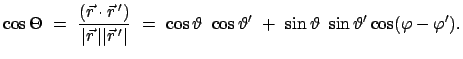
Für 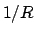 , wie es in der obigen Greenschen Funktion vorkommt, gibt es folgende Reihenentwicklung:
, wie es in der obigen Greenschen Funktion vorkommt, gibt es folgende Reihenentwicklung:
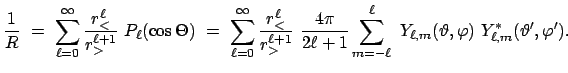
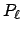 ist das Legendre-Polynom der Ordnung
ist das Legendre-Polynom der Ordnung 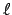 .
.
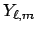 sind die Kugelflächenfunktionen.
Alle diese Funktionen werden in der Vorlesung ''Spezielle Funktionen'' behandelt.
sind die Kugelflächenfunktionen.
Alle diese Funktionen werden in der Vorlesung ''Spezielle Funktionen'' behandelt.
Eine wichtige Methode um Informationen über ein Objekt das nicht greifbar
ist (z.B. weil es unerreichbar weit weg ist oder seine
Groesse unter der Auflösung eines Mikroskops liegt), ist die Streuung.
Bei einem elastischen Streuvorgang werden Teilchen (oder Wellen) auf eine
das Untersuchungsobjekt geschossen und die abgelenkten Teilchen (oder Wellen)
werden nach Zahl (oder Intensität) und Richtung registriert. Ein einfaches
Beispiel ist die elastische Streuung an einer Kugel, s. die Simulation in
K5StreuungAnKugel.nb. Die
Streuung geladener Teilchen an einem fixen
punktförmigen Kern ist in
K5RutherfordScatt.nb
simuliert.
In §5.2.4 wurde die Streuung (E. scattering) eines
geladenen Teilchens, insbesondere
eines 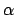 -Teilchens, an einem fixen Kern mit der Ladung
-Teilchens, an einem fixen Kern mit der Ladung 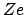 behandelt
und der Streuwinkel
behandelt
und der Streuwinkel  als Funktion des Stoßparameters
(E. impact parameter)
als Funktion des Stoßparameters
(E. impact parameter) 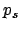 berechnet, Gl. (5.29).
In diesem Paragraph wird der Stoßparamter mit dem
Buchstaben
berechnet, Gl. (5.29).
In diesem Paragraph wird der Stoßparamter mit dem
Buchstaben 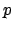 bezeichnet. Diese mikroskopische Betrachtungsweise ist
in Abb. 5.7(b) dargestellt: Ein Teilchen, dessen
Stoßparameter zwischen
bezeichnet. Diese mikroskopische Betrachtungsweise ist
in Abb. 5.7(b) dargestellt: Ein Teilchen, dessen
Stoßparameter zwischen
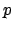 und
und
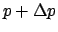 liegt, läuft ein und wird in den Streukegel
zwischen
liegt, läuft ein und wird in den Streukegel
zwischen  und
und
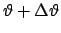 abgelenkt.
Es ist nicht möglich,
eine derartige detaillierte Messung durchzuführen. Beim realen
Experiment, Abb. 5.7(a), wird ein dünner Strahl von
abgelenkt.
Es ist nicht möglich,
eine derartige detaillierte Messung durchzuführen. Beim realen
Experiment, Abb. 5.7(a), wird ein dünner Strahl von
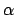 -Teilchen auf
eine Folie des zu untersuchenden Elements (das Target = Ziel)
geschossen, an irgendeinem Kern in den Kegel zwischen
-Teilchen auf
eine Folie des zu untersuchenden Elements (das Target = Ziel)
geschossen, an irgendeinem Kern in den Kegel zwischen  und
und
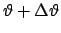 abgelenkt und trifft auf den Leuchtschirm in der
zugehörigen Zone der Fläche
abgelenkt und trifft auf den Leuchtschirm in der
zugehörigen Zone der Fläche 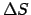 . Man muß mit einer großen
Zahl von
. Man muß mit einer großen
Zahl von 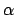 -Teilchen und Atomkernen (=Streuzentren) arbeiten.
Die Parameter des einzelnen Vorganges sind nicht beobachtbar;
statistische Überlegungen ersetzen dann die Unkenntnis des
Einzelvorganges. In diesem Zusammenhang wird der Begriff des
Wirkungsquerschnitts (E. cross section) eingeführt.
-Teilchen und Atomkernen (=Streuzentren) arbeiten.
Die Parameter des einzelnen Vorganges sind nicht beobachtbar;
statistische Überlegungen ersetzen dann die Unkenntnis des
Einzelvorganges. In diesem Zusammenhang wird der Begriff des
Wirkungsquerschnitts (E. cross section) eingeführt.
Abbildung 5.7:
Streuung makroskopisch (a) und mikroskopisch (b) betrachtet
|
[]
![\includegraphics[scale=0.7]{k5_streumakro}](img1007.gif) []
[]
![\includegraphics[scale=0.7]{k5_streumikro}](img1008.gif) |
Der Wirkungsquerschnitt 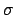 ist ein Maß für die Wahrscheinlichkeit
des Eintretens eines bestimmten Ereignissses (z.B. Neutroneneinfang,
durch Neutronen induzierte Kernspaltung, Streuung von Teilchen,...).
Man stellt sich vor, daß jeder Atomkern einem einfallenden
Teilchenstrom eine effektive Fläche (meist gemessen in barn,
1 b =
ist ein Maß für die Wahrscheinlichkeit
des Eintretens eines bestimmten Ereignissses (z.B. Neutroneneinfang,
durch Neutronen induzierte Kernspaltung, Streuung von Teilchen,...).
Man stellt sich vor, daß jeder Atomkern einem einfallenden
Teilchenstrom eine effektive Fläche (meist gemessen in barn,
1 b = 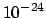 cm
cm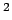 ) entgegensetzt, sodaß, wenn ein Teilchen innerhalb
dieser Fläche auftrifft oder durch diese fliegt, eine bestimmte Reaktion
auftritt. Der Wirkungsquerschnitt gilt dann für diese Reaktion.
) entgegensetzt, sodaß, wenn ein Teilchen innerhalb
dieser Fläche auftrifft oder durch diese fliegt, eine bestimmte Reaktion
auftritt. Der Wirkungsquerschnitt gilt dann für diese Reaktion.
Bei vielen Vorgängen, gerade auch bei der Streuung, wird das aus Richtung
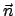 einlaufende Teilchen in Richtung
einlaufende Teilchen in Richtung
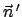 abgelenkt. Mit diesem
Vorgang wird der differentielle Wirkungsquerschnitt(E.: differential
cross section) verknüpft. Wenn man nur daran interessiert ist, ob die Reaktion
überhaupt stattfindet, dann wird über alle Raumrichtungen integriert;
man spricht vom totalen oder integralen Wirkungsquerschnitt
(E.: total cross section).
abgelenkt. Mit diesem
Vorgang wird der differentielle Wirkungsquerschnitt(E.: differential
cross section) verknüpft. Wenn man nur daran interessiert ist, ob die Reaktion
überhaupt stattfindet, dann wird über alle Raumrichtungen integriert;
man spricht vom totalen oder integralen Wirkungsquerschnitt
(E.: total cross section).
Der eben beschriebene Sachverhalt wird nun in Formeln ausgedrückt. In der
mikroskopischen Betrachtungsweise wird die Streuung an einem fixen Streukern
(= Atom) betrachtet. Auf diesen strömt ein Strahl von Teilchen mit der homogenen
Stromdichte 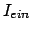 ; die Strahlrichtung ist durch den Einheitsvektor
; die Strahlrichtung ist durch den Einheitsvektor 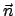 gegeben. Die Teilchen, die das durch die Koordinaten
gegeben. Die Teilchen, die das durch die Koordinaten 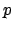 und
und 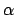 bestimmte
Flächenelement
bestimmte
Flächenelement
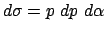 durchqueren, werden in das Raumwinkelelement
durchqueren, werden in das Raumwinkelelement
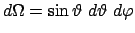 gestreut; diese lieferen den
differentiellen Streustrom
gestreut; diese lieferen den
differentiellen Streustrom 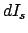 . Das Raumwinkelelement ist ein pyramidenähnliches
Gebilde mit der durch die Winkel
. Das Raumwinkelelement ist ein pyramidenähnliches
Gebilde mit der durch die Winkel  und
und  bestimmten Achse
bestimmten Achse
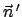 . Die Maßeinheit des einfallenden Stromes,
. Die Maßeinheit des einfallenden Stromes, 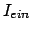 , ist
Teilchen/m
, ist
Teilchen/m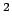 /sec;
die des Streustroms,
/sec;
die des Streustroms, 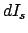 , ist Teilchen/sec (da der Raumwinkel dimensionslos ist):
, ist Teilchen/sec (da der Raumwinkel dimensionslos ist):
Im allgemeinsten Fall ist der Streuer nicht kugel- oder achsialsymmetrisch,
dann erfährt das Streuteilchen auch eine Ablenkung in azimuthaler Richtung,
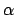 und
und 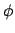 sind daher verschieden. Der differentielle Wirkungsquerschnitt
sind daher verschieden. Der differentielle Wirkungsquerschnitt
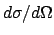 ist dann gegeben durch:
ist dann gegeben durch:
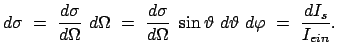 |
(541) |
Der integrale Wirkungsquerschnitt ist dann:
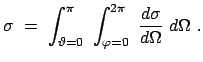 |
(542) |
Im realen Experiment durchquert der Teilchenstrahl eine Folie der Dicke  und
schneidet auf dieser eine Fläche
und
schneidet auf dieser eine Fläche 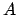 aus. Während der Beobachtungszeit fallen
aus. Während der Beobachtungszeit fallen
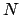 Teilchen auf das Target; der einfallende Strom ist also:
Von den einlaufenden Teilchen werden während des selben Zeitintervalles
Teilchen auf das Target; der einfallende Strom ist also:
Von den einlaufenden Teilchen werden während des selben Zeitintervalles
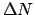 Teilchen in das Raumwinkelelement
Teilchen in das Raumwinkelelement
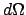 um
um
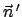 gestreut und treffen auf
eine Zone
gestreut und treffen auf
eine Zone
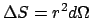 des kugelförmigen Leuchtschirms.
Die Folie muß so dünn
sein, daß jedes einlaufende Teilchen höchstens von einem Atom(kern) des
Targetmaterials gestreut wird. Im vom Strahl durchquerten Volumen des Targets
befinden sich
des kugelförmigen Leuchtschirms.
Die Folie muß so dünn
sein, daß jedes einlaufende Teilchen höchstens von einem Atom(kern) des
Targetmaterials gestreut wird. Im vom Strahl durchquerten Volumen des Targets
befinden sich
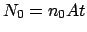 Streuer;
Streuer; 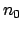 ist die Dichte der streuenden Atome.
Der Wirkungsquerschnitt ist auf das einzelne Atom bezogen. Daher muß die
Zahl der gestreuten Teilchen durch die Zahl der streuenden dividiert werden.
Dies gibt für den differentiellen Wirkungsquerschnitt:
ist die Dichte der streuenden Atome.
Der Wirkungsquerschnitt ist auf das einzelne Atom bezogen. Daher muß die
Zahl der gestreuten Teilchen durch die Zahl der streuenden dividiert werden.
Dies gibt für den differentiellen Wirkungsquerschnitt:
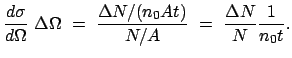 |
(543) |
Die rechte Seite dieser Gleichung enthält nur makroskopische Größen,
die aus Messungen bestimmt werden können.
Bei den hier betrachteten Problemen ist der Strahl homogen. Die Streuer sind sphärisch
symmetrisch. Es gibt daher keine Abhängigkeit von den Azimuthwinkeln  bzw.
bzw.
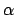 . Es kann über diese Winkel integriert werden. Dann wird
. Es kann über diese Winkel integriert werden. Dann wird 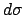 ein
ringförmiges Flächenelement und
ein
ringförmiges Flächenelement und 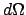 ein Hohlkegel (s. Abb. 5.7):
ein Hohlkegel (s. Abb. 5.7):
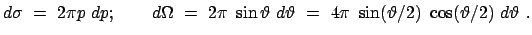 |
(544) |
Damit ergibt sich für den differentiellen Wirkungsquerschnitt:
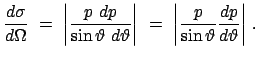 |
(545) |
Die Striche für den Absolutbetrag wurden eingefügt, weil in vielen Fällen
die Ableitung
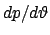 negativ ist (nämlich dann,wenn der Streuwinkel
negativ ist (nämlich dann,wenn der Streuwinkel  mit
zunehmendem Stoßparameter
mit
zunehmendem Stoßparameter 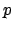 abnimmt), der Wirkungsquerschnitt aber positiv sein muß.
abnimmt), der Wirkungsquerschnitt aber positiv sein muß.
Zur Berechnung des Wirkungsquerschnitts wird noch eine Beziehung zwischen dem
Flächenelement 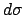 und dem Raumwinkelelement
und dem Raumwinkelelement 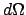 benötigt, bzw.
zwischen dem Stoßparameter
benötigt, bzw.
zwischen dem Stoßparameter 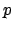 und dem Streuwinkel
und dem Streuwinkel  . Diese findet man,
indem man die Bahn in dem vorgegebenen Kraftfeld als Funktion des Stoßparameters
berechnet. Dies ist die Stelle, an der die Eigenschaften des tatsächlichen oder
angenommenen Kraftfeldes in den Wirkungsquerschnitt eingehen.
. Diese findet man,
indem man die Bahn in dem vorgegebenen Kraftfeld als Funktion des Stoßparameters
berechnet. Dies ist die Stelle, an der die Eigenschaften des tatsächlichen oder
angenommenen Kraftfeldes in den Wirkungsquerschnitt eingehen.
Die Lösung des Keplerproblems für die Streuung eines Teilchens der Masse
 und der Ladung
und der Ladung 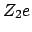 an einem fixen Kern der Ladung
an einem fixen Kern der Ladung 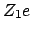 gibt folgende
Beziehung zwischen dem Streuwinkel
gibt folgende
Beziehung zwischen dem Streuwinkel
 und Stoßparamter
und Stoßparamter 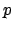 ,
Gl. (5.29):
,
Gl. (5.29):
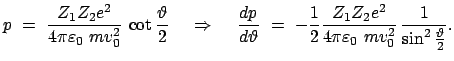 |
(546) |
Abbildung:
Streuung einer punktförmigen Ladung an einem fixen punktförmigen
Kern für verschiedene Werte des Stoßparameters; der Kern ist unsichtbar
klein im Koordinatenursprung. Links: Beide Ladungen haben verschiedenes
Vorzeichen. Rechts: Abstoßung ungleichnamiger Ladungen.
|
![\includegraphics[width=16cm]{k5_streu_punkt_lad}](img1037.gif) |
Die Streubahnen für verschiedene Werte des Stoßparameters sind in Abb. 5.9
dargestellt. Obwohl die Streubahnen in ihrem Verlauf um den Kern unterschiedliches
Aussehen haben - je nach dem Produkt der Vorzeichen der beiden Ladungen, -
erhält man für den Wirkungsquerschnitt in beiden Fällen das gleiche Resultat.
Obige Beziehung zwischen Stoßparameter 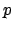 und Streuwinkel
und Streuwinkel  ist in Abb. 5.10(a) gezeigt.
Setzt man diese Ausdrücke und Gl. (5.44) in Gl. (5.45)
ein, ergibt sich für die Streuung des oben angeführten Streuteilchens an einem
fixen Kern mit Ladung
ist in Abb. 5.10(a) gezeigt.
Setzt man diese Ausdrücke und Gl. (5.44) in Gl. (5.45)
ein, ergibt sich für die Streuung des oben angeführten Streuteilchens an einem
fixen Kern mit Ladung 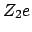 der differentielle Wirkungsquerschnitt
der differentielle Wirkungsquerschnitt
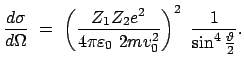 |
(547) |
Dieser ist in Abb. 5.10(b) gezeichnet.
Das obige Resultat führt bei der Berechnung des integralen Wirkungsquerschnitts,
wie er in Gl. (5.42) definiert ist, zu einer Schrwierigkeit.
Der Integrand von
ist singulär
für kleine  , also für Teilchen mit sehr großem
Stoßparameter
, also für Teilchen mit sehr großem
Stoßparameter 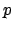 . Für solche Werte versagt das verwendete Modell,
in dem nur ein Streuer, dessen Kraft bis ins Unendliche reicht, in Betracht gezogen
wird. Im Target sind ja viele Atome; deswegen kann sich der Wert des Stoßparameters
nur bis zu einem endlichen Wert erstrecken, der durch den Abstand zwischen den Atomen
(z.B. die Gitterkonstante bei einem Kristall) festgelegt ist.
. Für solche Werte versagt das verwendete Modell,
in dem nur ein Streuer, dessen Kraft bis ins Unendliche reicht, in Betracht gezogen
wird. Im Target sind ja viele Atome; deswegen kann sich der Wert des Stoßparameters
nur bis zu einem endlichen Wert erstrecken, der durch den Abstand zwischen den Atomen
(z.B. die Gitterkonstante bei einem Kristall) festgelegt ist.
Den integralen Wirkungsquerschnitt 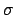 kann man aus folgender Überlegung
erhalten (Voraussetzung ist, daß sich die Wirkungsbereiche der Kerne
nicht gegenseitig überdecken, also müssen die Targets
hinreichend dünn sein):
kann man aus folgender Überlegung
erhalten (Voraussetzung ist, daß sich die Wirkungsbereiche der Kerne
nicht gegenseitig überdecken, also müssen die Targets
hinreichend dünn sein):
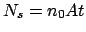 ist die Anzahl der Streuer in dem Bereich des Targets,
auf den der Strahl mit Querchnitt
ist die Anzahl der Streuer in dem Bereich des Targets,
auf den der Strahl mit Querchnitt 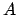 fällt;
fällt;  ist die Dicke der Targetfolie.
ist die Dicke der Targetfolie.
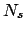 geteilt durch die Fläche des Strahls gibt die Fläche, die der einzelne
Streuer (hier der Atomkern über sein elektrisches Feld) den in seinen Bereich
eindringenden Teilchen des Strahls darbietet; dies ist der gesuchte
integrale Wirkungsquerschnitt:
geteilt durch die Fläche des Strahls gibt die Fläche, die der einzelne
Streuer (hier der Atomkern über sein elektrisches Feld) den in seinen Bereich
eindringenden Teilchen des Strahls darbietet; dies ist der gesuchte
integrale Wirkungsquerschnitt:
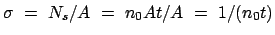 .
.
Ein anderes Modell besteht darin, daß die Abschirmung durch die Elektronenhülle
berücksichtigt wird. Dann ist die Reichweite der Kraft der Kernladung begrenzt.
Dies wird in einer Übung behandelt.
Beobachtet wird eine Streuung in den Raumwinkelbereich
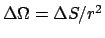 (hier ist angenommen, daß
der Leuchtschirm eine Kugel vom Radius
(hier ist angenommen, daß
der Leuchtschirm eine Kugel vom Radius  ist; eine andere Gestalt desselben
erfordert Korrekturen). Dann ergibt sich aus Gl. (5.43)
die Wahrscheinlichkeit für Streuung von Teilchen in den
Bereich
ist; eine andere Gestalt desselben
erfordert Korrekturen). Dann ergibt sich aus Gl. (5.43)
die Wahrscheinlichkeit für Streuung von Teilchen in den
Bereich
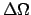 :
:
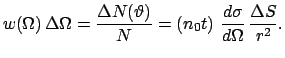 |
(548) |
Nach obiger Ableitung (bei der vorausgesetzt worden ist, daß der Kern
punktförmig und von einem
Coulombfeld umgeben ist) muß bei konstanten
Versuchs- und Beobachtungsbedingungen die Anzahl der pro
Flächeneinheit auf  auftreffenden
auftreffenden  -Teilchen
umgekehrt proportional der vierten Potenz des halben Streuwinkels
sein.
-Teilchen
umgekehrt proportional der vierten Potenz des halben Streuwinkels
sein.
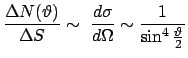 |
(549) |
Da der Leuchtschirm beim Auftreffen der 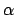 -Teilchen aufblitzt
(Szintillationen), kann diese Zahl ausgezählt werden. Das
Experiment zeigt die Gültigkeit obiger Formel.
-Teilchen aufblitzt
(Szintillationen), kann diese Zahl ausgezählt werden. Das
Experiment zeigt die Gültigkeit obiger Formel.
Aus Abweichungen
bei Rückstreuungen konnte man auf die Größenordung des
Kernradius schließen und fand
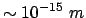 . Dieser
kleine Wert vermag die scharfen Knicke mancher Spuren von
. Dieser
kleine Wert vermag die scharfen Knicke mancher Spuren von
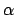 -Teilchen in Nebelkammern erklären.
Durch gleichzeitige Messung von
-Teilchen in Nebelkammern erklären.
Durch gleichzeitige Messung von
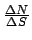 und
und 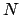 konnte aus Gl. (5.48) und Gl. (5.47)
die Kernladungszahl
konnte aus Gl. (5.48) und Gl. (5.47)
die Kernladungszahl 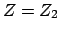 bestimmt werden. Es ergab sich, daß
diese gleich der Ordnungszahl des Elements im Periodensystem
war (van der Brook (1912)).
bestimmt werden. Es ergab sich, daß
diese gleich der Ordnungszahl des Elements im Periodensystem
war (van der Brook (1912)).
Ergänzende Literatur zu diesem Paragraphen:
R.E. Johnson: Introduction to Atomic and Molecular Collissions.
Plenum Press (1982).
Christian Sommer
2003-01-27
![]() gewählt. Die Stärke der Kraft ist nur eine Funktion
des Abstandes vom Zentrum:
gewählt. Die Stärke der Kraft ist nur eine Funktion
des Abstandes vom Zentrum:
![]() Die
Die ![]() -Achse soll mit dem
Drehimpulsvektor
-Achse soll mit dem
Drehimpulsvektor ![]() zusammenfallen. In der Bahnebene
(=
zusammenfallen. In der Bahnebene
(= ![]() -Ebene) führt man Polarkoordinaten
-Ebene) führt man Polarkoordinaten ![]() ein:
ein:
![]() , das
Keplerproblem
, das
Keplerproblem ![]() und das Potential
und das Potential
![]() mit elementaren Funktionen ausgeführt werden. Das Integral (5.11)
kann beim
Keplerproblem ausgeführt, der resultierende Ausdruck aber nicht mehr analytisch
invertiert werden. Für ungefähr 18 andere Zentralpotentiale kann das Integral
(5.10) mittels elliptischer Integrale ausgeführt werden.
(Goldstein [1], S. 80 - 86). Das Theorem von Newton
(K8. Ü5) ermöglicht es, die bekannte Lösung für ein Kraftfeld
mit elementaren Funktionen ausgeführt werden. Das Integral (5.11)
kann beim
Keplerproblem ausgeführt, der resultierende Ausdruck aber nicht mehr analytisch
invertiert werden. Für ungefähr 18 andere Zentralpotentiale kann das Integral
(5.10) mittels elliptischer Integrale ausgeführt werden.
(Goldstein [1], S. 80 - 86). Das Theorem von Newton
(K8. Ü5) ermöglicht es, die bekannte Lösung für ein Kraftfeld ![]() zu
benutzen, um auch den Fall zu lösen, wo zu
zu
benutzen, um auch den Fall zu lösen, wo zu ![]() noch eine zusätzliche
Kraft
noch eine zusätzliche
Kraft ![]() hinzukommt. Die numerische Auswertung der Integrale und der
Inversionen bereitet auf einem Computer keine besonderen Probleme, wenn man
beachtet, daß die Wurzel im Nenner an den Umkehrpunkten Null, das Integral
also schwach singulär wird. Zweckmässiger ist es aber, die Newtonschen
Bewegungsgleichungen in rechtwinkligen Koordinaten direkt durch numerische
Integration (z.B. Runge-Kutta Verfahren, NDSolve[...] in Mathematica) zu
lösen.
hinzukommt. Die numerische Auswertung der Integrale und der
Inversionen bereitet auf einem Computer keine besonderen Probleme, wenn man
beachtet, daß die Wurzel im Nenner an den Umkehrpunkten Null, das Integral
also schwach singulär wird. Zweckmässiger ist es aber, die Newtonschen
Bewegungsgleichungen in rechtwinkligen Koordinaten direkt durch numerische
Integration (z.B. Runge-Kutta Verfahren, NDSolve[...] in Mathematica) zu
lösen.
![]() voraus. Gl. (5.5) wird umgeschrieben:
voraus. Gl. (5.5) wird umgeschrieben:
![\includegraphics[scale=0.9]{k5_zentralpot}](img838.gif)
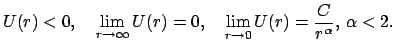
![]() ist konstant, da
ist konstant, da
![]() Zentralkraft ist. Die Lösungen unterscheiden sich etwas,
je nachdem, ob
Zentralkraft ist. Die Lösungen unterscheiden sich etwas,
je nachdem, ob ![]() oder
oder ![]() ist.
ist.
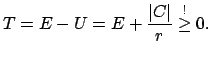
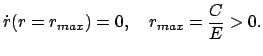
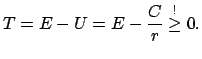
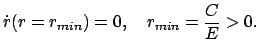
![\includegraphics[scale=0.84]{k5_bewegmog_a}](img874.gif) []
[]
![\includegraphics[scale=0.86]{k5_bewegmog_b}](img875.gif)
![]() :
:
![]() und der
Gesamtenergie
und der
Gesamtenergie ![]() ist der Laplace-Lenzsche Vektor :
ist der Laplace-Lenzsche Vektor :
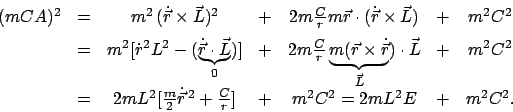
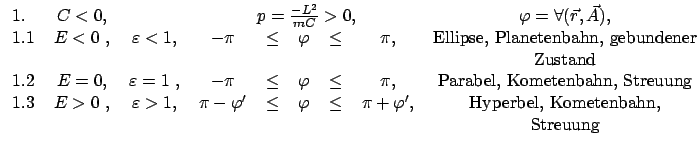
![]() ) durchläuft der geladene Massenpunkt den anderen
Zweig der Hyperbel. In Polarkoordinaten lautet dessen Gleichung:
) durchläuft der geladene Massenpunkt den anderen
Zweig der Hyperbel. In Polarkoordinaten lautet dessen Gleichung:
![]() bedeutet, daß der radiale Strahl in
entgegegesetzter Richtung zu verfolgen ist
(s. Abb. 5.5(b)). Dann ergibt sich
durch Vergleich obiger Gleichung mit Gl. (5.22):
bedeutet, daß der radiale Strahl in
entgegegesetzter Richtung zu verfolgen ist
(s. Abb. 5.5(b)). Dann ergibt sich
durch Vergleich obiger Gleichung mit Gl. (5.22):
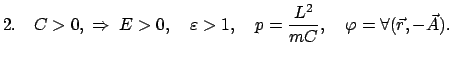
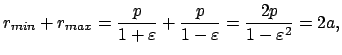
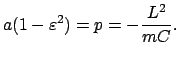
![]() ),
d.h. für die ganze Ellipse (Fläche =
),
d.h. für die ganze Ellipse (Fläche = ![]() ):
):
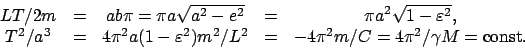
![]() , Ladungszahl
, Ladungszahl ![]() )
wird an einem fixen Targetteilchen (mit Ladung
)
wird an einem fixen Targetteilchen (mit Ladung ![]() )
gestreut;
)
gestreut;
![]() ; doch gilt das Resultat auch für
; doch gilt das Resultat auch für ![]() ,
wenn
,
wenn ![]() ist.
ist.
![]() ). Das Streuteilchen kommt mit
Geschwindigkeit
). Das Streuteilchen kommt mit
Geschwindigkeit ![]() aus dem Unendlichen. Würde es keine Ablenkung
erfahren, dann wäre
seine Bahn eine Gerade, die vom Kern den Normalabstand
aus dem Unendlichen. Würde es keine Ablenkung
erfahren, dann wäre
seine Bahn eine Gerade, die vom Kern den Normalabstand ![]() hätte;
deshalb
heißt
hätte;
deshalb
heißt ![]() der Stoßparameter. Aufgrund seiner Ladung wird
das Streuteilchen abgelenkt, es wird um den Winkel
der Stoßparameter. Aufgrund seiner Ladung wird
das Streuteilchen abgelenkt, es wird um den Winkel ![]() gestreut
(Abb. 5.5).
gestreut
(Abb. 5.5).
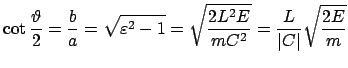
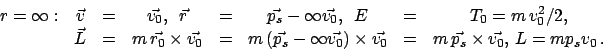
![]() (bzw. Punktladung
(bzw. Punktladung ![]() ) im Innern einer
homogen mit Masse (Ladung) belegten Kugelschale ist Null.
) im Innern einer
homogen mit Masse (Ladung) belegten Kugelschale ist Null.
![]() haben.
haben.
![]() , die von der auf der Schale homogen
verteilten Masse
, die von der auf der Schale homogen
verteilten Masse ![]() ausgeübt wird, ist identisch mit der Kraft, die
bei Abwesenheit der Flächenbelegung
ausgeübt wird, ist identisch mit der Kraft, die
bei Abwesenheit der Flächenbelegung ![]() eine Punktmasse
eine Punktmasse ![]() ausübt,
die im Mittelpunkt der Schale angebracht ist. Dazu wird gezeigt, daß das
Potential einer Masse
ausübt,
die im Mittelpunkt der Schale angebracht ist. Dazu wird gezeigt, daß das
Potential einer Masse ![]() (einer Ladung
(einer Ladung ![]() ), die über eine
Kugelschale
), die über eine
Kugelschale ![]() vom Radius
vom Radius ![]() homogen verteilt ist, Gl. (5.31),
dasselbe ist wie das einer Punktmasse
homogen verteilt ist, Gl. (5.31),
dasselbe ist wie das einer Punktmasse ![]() (einer Punktladung
(einer Punktladung ![]() ),
die sich im Mittelpunkt
),
die sich im Mittelpunkt ![]() der Kugelschale
der Kugelschale ![]() befindet. Zunächst
wird das Potential
befindet. Zunächst
wird das Potential ![]() im Punkt
im Punkt ![]() , das von einer
mit der Massendichte
, das von einer
mit der Massendichte ![]() belegten Kugelzone
erzeugt wird, berechnet (Abb. 5.6(b)):
belegten Kugelzone
erzeugt wird, berechnet (Abb. 5.6(b)):
![$\displaystyle dR = [r^{2} - 2rr' \cos \vartheta' + r'^{2}]^{-\frac{1}{2}} ...
...sin\vartheta'
d\vartheta' = rr' \sin\vartheta' \frac{d\vartheta'}{R},
$](img950.gif)
![]() ist die Kraft Null, daher das
Potential konstant. Diese Konstante wird so gewählt, daß die
potentielle Energie stetig ist :
ist die Kraft Null, daher das
Potential konstant. Diese Konstante wird so gewählt, daß die
potentielle Energie stetig ist :
![]() (Punktladung
(Punktladung ![]() ) im Inneren
einer radialsymmetrischen Massen-(Ladungs-)verteilung im Abstand
) im Inneren
einer radialsymmetrischen Massen-(Ladungs-)verteilung im Abstand ![]() vom Symmetriezentrum, dann übt der außerhalb
vom Symmetriezentrum, dann übt der außerhalb ![]() gelegene Anteil der
Verteilung keine
Kraft auf
gelegene Anteil der
Verteilung keine
Kraft auf ![]() (
(![]() ) aus. Daher wirkt auf
) aus. Daher wirkt auf ![]() (
(![]() ) nur der innerhalb
von
) nur der innerhalb
von ![]() gelegene Anteil der Massen-(Ladungs-)verteilung; dieser kann
so berücksichtigt werden als wenn er im Symmetriezentrum
angebracht wäre. Bei der Berechnung des Potentials muß aber
darauf geachtet werden, daß der außerhalb
gelegene Anteil der Massen-(Ladungs-)verteilung; dieser kann
so berücksichtigt werden als wenn er im Symmetriezentrum
angebracht wäre. Bei der Berechnung des Potentials muß aber
darauf geachtet werden, daß der außerhalb ![]() liegende Anteil der
Massenverteilung einen Beitrag zum Potential liefert. Mit diesen
Überlegungen läßt sich die potentielle Energie einer Punktmasse
liegende Anteil der
Massenverteilung einen Beitrag zum Potential liefert. Mit diesen
Überlegungen läßt sich die potentielle Energie einer Punktmasse ![]() (einer Punktladung
(einer Punktladung ![]() ) im Inneren und Äußeren einer sphärischen
Massenverteilung
) im Inneren und Äußeren einer sphärischen
Massenverteilung ![]() berechnen. Die Gesamtmasse
berechnen. Die Gesamtmasse ![]() beträgt:
beträgt:
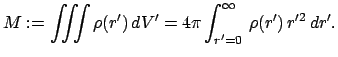
![]() ist in den obigen
Formeln
ist in den obigen
Formeln
![]() durch die Ladung
durch die Ladung ![]() (cgs-Einheiten) bzw.
(cgs-Einheiten) bzw.
![]() (MKSA-Einheiten) zu ersetzen.
(MKSA-Einheiten) zu ersetzen.
![]() gegeben. Die Gesamtmasse
gegeben. Die Gesamtmasse ![]() (analog dazu die Gesamtladung
(analog dazu die Gesamtladung ![]() )
ist durch das folgende Integral definiert:
)
ist durch das folgende Integral definiert:
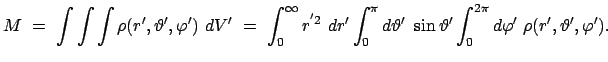
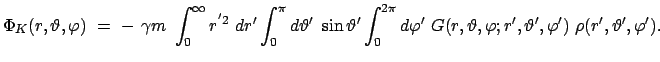
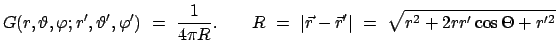
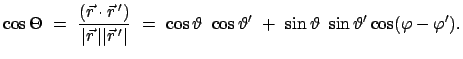
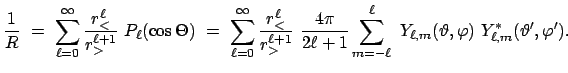
![]() -Teilchens, an einem fixen Kern mit der Ladung
-Teilchens, an einem fixen Kern mit der Ladung ![]() behandelt
und der Streuwinkel
behandelt
und der Streuwinkel ![]() als Funktion des Stoßparameters
(E. impact parameter)
als Funktion des Stoßparameters
(E. impact parameter) ![]() berechnet, Gl. (5.29).
In diesem Paragraph wird der Stoßparamter mit dem
Buchstaben
berechnet, Gl. (5.29).
In diesem Paragraph wird der Stoßparamter mit dem
Buchstaben ![]() bezeichnet. Diese mikroskopische Betrachtungsweise ist
in Abb. 5.7(b) dargestellt: Ein Teilchen, dessen
Stoßparameter zwischen
bezeichnet. Diese mikroskopische Betrachtungsweise ist
in Abb. 5.7(b) dargestellt: Ein Teilchen, dessen
Stoßparameter zwischen
![]() und
und
![]() liegt, läuft ein und wird in den Streukegel
zwischen
liegt, läuft ein und wird in den Streukegel
zwischen ![]() und
und
![]() abgelenkt.
Es ist nicht möglich,
eine derartige detaillierte Messung durchzuführen. Beim realen
Experiment, Abb. 5.7(a), wird ein dünner Strahl von
abgelenkt.
Es ist nicht möglich,
eine derartige detaillierte Messung durchzuführen. Beim realen
Experiment, Abb. 5.7(a), wird ein dünner Strahl von
![]() -Teilchen auf
eine Folie des zu untersuchenden Elements (das Target = Ziel)
geschossen, an irgendeinem Kern in den Kegel zwischen
-Teilchen auf
eine Folie des zu untersuchenden Elements (das Target = Ziel)
geschossen, an irgendeinem Kern in den Kegel zwischen ![]() und
und
![]() abgelenkt und trifft auf den Leuchtschirm in der
zugehörigen Zone der Fläche
abgelenkt und trifft auf den Leuchtschirm in der
zugehörigen Zone der Fläche ![]() . Man muß mit einer großen
Zahl von
. Man muß mit einer großen
Zahl von ![]() -Teilchen und Atomkernen (=Streuzentren) arbeiten.
Die Parameter des einzelnen Vorganges sind nicht beobachtbar;
statistische Überlegungen ersetzen dann die Unkenntnis des
Einzelvorganges. In diesem Zusammenhang wird der Begriff des
Wirkungsquerschnitts (E. cross section) eingeführt.
-Teilchen und Atomkernen (=Streuzentren) arbeiten.
Die Parameter des einzelnen Vorganges sind nicht beobachtbar;
statistische Überlegungen ersetzen dann die Unkenntnis des
Einzelvorganges. In diesem Zusammenhang wird der Begriff des
Wirkungsquerschnitts (E. cross section) eingeführt.
![]() einlaufende Teilchen in Richtung
einlaufende Teilchen in Richtung
![]() abgelenkt. Mit diesem
Vorgang wird der differentielle Wirkungsquerschnitt(E.: differential
cross section) verknüpft. Wenn man nur daran interessiert ist, ob die Reaktion
überhaupt stattfindet, dann wird über alle Raumrichtungen integriert;
man spricht vom totalen oder integralen Wirkungsquerschnitt
(E.: total cross section).
abgelenkt. Mit diesem
Vorgang wird der differentielle Wirkungsquerschnitt(E.: differential
cross section) verknüpft. Wenn man nur daran interessiert ist, ob die Reaktion
überhaupt stattfindet, dann wird über alle Raumrichtungen integriert;
man spricht vom totalen oder integralen Wirkungsquerschnitt
(E.: total cross section).
![]() ; die Strahlrichtung ist durch den Einheitsvektor
; die Strahlrichtung ist durch den Einheitsvektor ![]() gegeben. Die Teilchen, die das durch die Koordinaten
gegeben. Die Teilchen, die das durch die Koordinaten ![]() und
und ![]() bestimmte
Flächenelement
bestimmte
Flächenelement
![]() durchqueren, werden in das Raumwinkelelement
durchqueren, werden in das Raumwinkelelement
![]() gestreut; diese lieferen den
differentiellen Streustrom
gestreut; diese lieferen den
differentiellen Streustrom ![]() . Das Raumwinkelelement ist ein pyramidenähnliches
Gebilde mit der durch die Winkel
. Das Raumwinkelelement ist ein pyramidenähnliches
Gebilde mit der durch die Winkel ![]() und
und ![]() bestimmten Achse
bestimmten Achse
![]() . Die Maßeinheit des einfallenden Stromes,
. Die Maßeinheit des einfallenden Stromes, ![]() , ist
Teilchen/m
, ist
Teilchen/m![]() /sec;
die des Streustroms,
/sec;
die des Streustroms, ![]() , ist Teilchen/sec (da der Raumwinkel dimensionslos ist):
, ist Teilchen/sec (da der Raumwinkel dimensionslos ist):
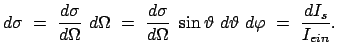
![]() bzw.
bzw.
![]() . Es kann über diese Winkel integriert werden. Dann wird
. Es kann über diese Winkel integriert werden. Dann wird ![]() ein
ringförmiges Flächenelement und
ein
ringförmiges Flächenelement und ![]() ein Hohlkegel (s. Abb. 5.7):
ein Hohlkegel (s. Abb. 5.7):
![]() und dem Raumwinkelelement
und dem Raumwinkelelement ![]() benötigt, bzw.
zwischen dem Stoßparameter
benötigt, bzw.
zwischen dem Stoßparameter ![]() und dem Streuwinkel
und dem Streuwinkel ![]() . Diese findet man,
indem man die Bahn in dem vorgegebenen Kraftfeld als Funktion des Stoßparameters
berechnet. Dies ist die Stelle, an der die Eigenschaften des tatsächlichen oder
angenommenen Kraftfeldes in den Wirkungsquerschnitt eingehen.
. Diese findet man,
indem man die Bahn in dem vorgegebenen Kraftfeld als Funktion des Stoßparameters
berechnet. Dies ist die Stelle, an der die Eigenschaften des tatsächlichen oder
angenommenen Kraftfeldes in den Wirkungsquerschnitt eingehen.
![]() und der Ladung
und der Ladung ![]() an einem fixen Kern der Ladung
an einem fixen Kern der Ladung ![]() gibt folgende
Beziehung zwischen dem Streuwinkel
gibt folgende
Beziehung zwischen dem Streuwinkel
![]() und Stoßparamter
und Stoßparamter ![]() ,
Gl. (5.29):
,
Gl. (5.29):
![\includegraphics[width=16cm]{k5_streu_punkt_lad}](img1037.gif)
![]() und Streuwinkel
und Streuwinkel ![]() ist in Abb. 5.10(a) gezeigt.
Setzt man diese Ausdrücke und Gl. (5.44) in Gl. (5.45)
ein, ergibt sich für die Streuung des oben angeführten Streuteilchens an einem
fixen Kern mit Ladung
ist in Abb. 5.10(a) gezeigt.
Setzt man diese Ausdrücke und Gl. (5.44) in Gl. (5.45)
ein, ergibt sich für die Streuung des oben angeführten Streuteilchens an einem
fixen Kern mit Ladung ![]() der differentielle Wirkungsquerschnitt
der differentielle Wirkungsquerschnitt
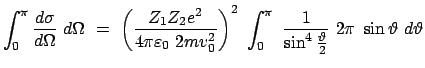
![\includegraphics[scale=0.63]{k5_streuwink}](img1040.gif) []
[]
![\includegraphics[scale=0.63]{k5_diff_wirk}](img1041.gif)
![]() kann man aus folgender Überlegung
erhalten (Voraussetzung ist, daß sich die Wirkungsbereiche der Kerne
nicht gegenseitig überdecken, also müssen die Targets
hinreichend dünn sein):
kann man aus folgender Überlegung
erhalten (Voraussetzung ist, daß sich die Wirkungsbereiche der Kerne
nicht gegenseitig überdecken, also müssen die Targets
hinreichend dünn sein):
![]() ist die Anzahl der Streuer in dem Bereich des Targets,
auf den der Strahl mit Querchnitt
ist die Anzahl der Streuer in dem Bereich des Targets,
auf den der Strahl mit Querchnitt ![]() fällt;
fällt; ![]() ist die Dicke der Targetfolie.
ist die Dicke der Targetfolie.
![]() geteilt durch die Fläche des Strahls gibt die Fläche, die der einzelne
Streuer (hier der Atomkern über sein elektrisches Feld) den in seinen Bereich
eindringenden Teilchen des Strahls darbietet; dies ist der gesuchte
integrale Wirkungsquerschnitt:
geteilt durch die Fläche des Strahls gibt die Fläche, die der einzelne
Streuer (hier der Atomkern über sein elektrisches Feld) den in seinen Bereich
eindringenden Teilchen des Strahls darbietet; dies ist der gesuchte
integrale Wirkungsquerschnitt:
![]() .
.
![]() (hier ist angenommen, daß
der Leuchtschirm eine Kugel vom Radius
(hier ist angenommen, daß
der Leuchtschirm eine Kugel vom Radius ![]() ist; eine andere Gestalt desselben
erfordert Korrekturen). Dann ergibt sich aus Gl. (5.43)
die Wahrscheinlichkeit für Streuung von Teilchen in den
Bereich
ist; eine andere Gestalt desselben
erfordert Korrekturen). Dann ergibt sich aus Gl. (5.43)
die Wahrscheinlichkeit für Streuung von Teilchen in den
Bereich
![]() :
:
![]() . Dieser
kleine Wert vermag die scharfen Knicke mancher Spuren von
. Dieser
kleine Wert vermag die scharfen Knicke mancher Spuren von
![]() -Teilchen in Nebelkammern erklären.
Durch gleichzeitige Messung von
-Teilchen in Nebelkammern erklären.
Durch gleichzeitige Messung von
![]() und
und ![]() konnte aus Gl. (5.48) und Gl. (5.47)
die Kernladungszahl
konnte aus Gl. (5.48) und Gl. (5.47)
die Kernladungszahl ![]() bestimmt werden. Es ergab sich, daß
diese gleich der Ordnungszahl des Elements im Periodensystem
war (van der Brook (1912)).
bestimmt werden. Es ergab sich, daß
diese gleich der Ordnungszahl des Elements im Periodensystem
war (van der Brook (1912)).