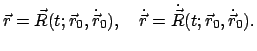Um Gesetzmäßigkeiten für die Bewegung von Körpern zu finden, wird zunächst
einmal noch eine weitere Vereinfachung der Beschreibung vorgenommen,
indem man voraussetzt, daß man die Bewegung des ganzen Körpers durch die
Bewegung eines einzelnen seiner Punkte ausreichend genau beschreiben kann.
Man sagt dann, daß man das Modell des Massenpunktes (E.: point mass) verwendet.
Als grundlegendes Axiom der Mechanik kann dann in Inertialsystemen die
Newtonsche Bewegungsgleichung
Da man die Abhängigkeit der Bewegungsvorgänge von äußeren Einflüssen
untersuchen will, ist es zweckmäßig, bei der Aufstellung von Gesetzen
Bezugssysteme heranzuziehen, in denen sich die Körper bei Abwesenheit
äußerer
Einflüsse besonders einfach bewegen. Dazu führt man den Begriff des
Inertialsystems (E.: inertial frame of reference) ein.
Die Existenz von Inertialsystemen ist dadurch noch nicht sichergestellt, doch
führt die Annahme ihres Vorhandenseins im weiteren Aufbau der Mechanik auf
keine Widersprüche, denn die obige Definition besagt, daß alles, was die
Körper zu einer nicht gleichförmigen, geraden Bewegung veranlaßt, als
äußerer Einfluß betrachtet wird. Es lassen sich nun tatsächlich Systeme
finden, in denen alle diese Einflüsse bestimmten Umständen eindeutig
zugeordnet werden können. (Z.B. Erdanziehung).
Man untersucht nun in Inertialsystemen Klassen von Bewegungsvorgängen, die
sich durch gemeinsame äußere Umstände auszeichnen, wie z.B. die Bewegungen
unter Einfluß der Schwere (Fall und Wurf), oder jene von Himmelskörpern,
oder von elektrisch geladenen Teilchen, usw. Man findet dann, daß sich für
alle solche Klassen Gesetze für die Beschleunigung aufstellen lassen, die
nur Konstanten enthalten, die für die ganze Klasse bezeichnend sind, aber
nicht solche, die die einzelnen Bewegungen kennzeichnen.
Z.B findet man für Fall und Wurf das Gesetz
Wenn man dieses System allgemein löst, dann hängt diese allgemeine Lösung
noch von 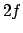 willkürlichen Integrationskonstanten ab.
Diese (und damit die spezifische Lösung für das betrachtete Problem) werden
spezifiziert durch vorgegebene Anfangswerte, die die Funktionen
willkürlichen Integrationskonstanten ab.
Diese (und damit die spezifische Lösung für das betrachtete Problem) werden
spezifiziert durch vorgegebene Anfangswerte, die die Funktionen
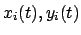 zum vorgegebenen Zeitpunkt
zum vorgegebenen Zeitpunkt 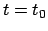 erfüllen sollen (Anfangsbedingungen):
erfüllen sollen (Anfangsbedingungen):
Über die Existenz der Lösungen gilt der folgende Satz:
In einem (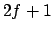 )-dimensionalen Bereich um
)-dimensionalen Bereich um
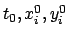 seien
seien
- die Funktionen
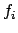 beschränkt:
beschränkt:
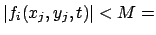 const. const.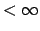 |
(37) |
- und gehorchen einer Lipschitzbedingung:
(die
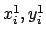 und
und
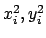 sind die Koordinaten
zweier Punkte aus dem
(
sind die Koordinaten
zweier Punkte aus dem
(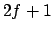 )-dimensionalen Bereich um die Anfangswerte): Dann existiert eine
eindeutige Lösung
)-dimensionalen Bereich um die Anfangswerte): Dann existiert eine
eindeutige Lösung
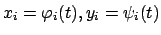 in einem Teilbereich um
in einem Teilbereich um 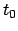 ,
wobei
,
wobei
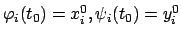 .
.
Die obigen Bedingungen haben folgende physikalische Bedeutung:
Die 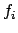 (i = 1,...,f) erfüllen als lineare Gleichungen die Bedingungen
(3.7) und (3.8) in trivialer Weise. Aus
(3.5), (3.6b) und (3.7) folgt:
(i = 1,...,f) erfüllen als lineare Gleichungen die Bedingungen
(3.7) und (3.8) in trivialer Weise. Aus
(3.5), (3.6b) und (3.7) folgt:
d.h., die Kraft muß im untersuchten Bereich beschränkt sein. Die
Lipschitzbedingung bedeutet, daß
der Zuwachs der die Funktion 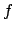 darstellenden Kurve beschränkt ist, d.h. der
Zuwachs der Kraft beim Fortschreiten im Raum muß beschränkt sein. Manchmal
wird anstelle der Lipschitzbedingung die etwas einschneidendere Bedingung der
Existenz stetiger partieller Ableitungen der Funktionen
darstellenden Kurve beschränkt ist, d.h. der
Zuwachs der Kraft beim Fortschreiten im Raum muß beschränkt sein. Manchmal
wird anstelle der Lipschitzbedingung die etwas einschneidendere Bedingung der
Existenz stetiger partieller Ableitungen der Funktionen 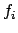 nach den
nach den
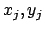 vorausgesetzt (W.I.Smirnow, Lehrgang der höheren Mathematik II, §2, Kap.
18).
vorausgesetzt (W.I.Smirnow, Lehrgang der höheren Mathematik II, §2, Kap.
18).
Obiger Existenzsatz gilt nur in einem gewissen Bereich um die Anfangswerte und
in einem beschränkten Zeitintervall. Oft sind in der Mechanik aber die
Lösungen und deren Verhalten für lange, wenn nicht für alle Zeiten von
Interesse.
Solche globale Aussagen sind aber nur in seltenen Fällen möglich, meist nur
in solchen, in denen sich analytische Ausdrücke für die Lösungen der
Bewegungsgleichungen angeben lassen.
Die Hauptaufgabe der Mechanik besteht in der Lösung der Newtonschen Bewegungsgleichung
(3.1) bzw. (3.5). Im allgemeinen stellen diese ein System von gekoppelten gewöhnlichen
Differentialgleichungen dar. In §3.3 ist angeführt worden, daß unter sehr allgemeinen
Bedingungen diese eine Lösung besitzen. Die praktische Berechnung derselben ist aber oft
sehr schwierig und es läßt sich kein universelles Verfahren angeben. In diesem
Paragraphen werden einige einfache Beispiele von Lösungsverfahren vorgeführt.
Freier Fall im Schwerefeld der Erde
Eine Masse  befindet sich im Schwerefeld in der Höhe
befindet sich im Schwerefeld in der Höhe 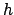 über dem Boden
(Abb. 3.1(a) ). Es ist zweckmäßig, das Koordinatensystem so zu legen, wie in
Abb. 3.1(b) gezeigt. Die Kraft ist dann:
über dem Boden
(Abb. 3.1(a) ). Es ist zweckmäßig, das Koordinatensystem so zu legen, wie in
Abb. 3.1(b) gezeigt. Die Kraft ist dann:
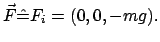 |
(39) |
Abbildung:
Links: a) Masse  im Schwerefeld in der Höhe
im Schwerefeld in der Höhe 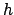 über dem Boden.
Mitte: b) Wahl des Koordinatensystems. Rechts: c) Vom Boden wird die Masse
über dem Boden.
Mitte: b) Wahl des Koordinatensystems. Rechts: c) Vom Boden wird die Masse  mit der Anfangsgeschwindigkeit
mit der Anfangsgeschwindigkeit 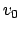 in die Höhe geworfen.
in die Höhe geworfen.
|
|
Die Bewegungsgleichung und deren allgemeine Lösung sind dann:
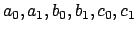 sind willkürliche
Integrationskonstanten. Man muß zu deren
Bestimmung die Anfangsbedingungen kennen.
sind willkürliche
Integrationskonstanten. Man muß zu deren
Bestimmung die Anfangsbedingungen kennen.
Physikalisch: Zur Zeit 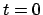 befinde
sich die Masse
befinde
sich die Masse  in der Höhe
in der Höhe 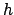 in Ruhe.
in Ruhe.
Mathematisch:
Einsetzen in die allg. Lösung gibt:
Wir erhalten also die spezielle Lösung für unser Problem:
Durch die physikalische Situation ergibt sich eine Einschränkung des
Intervalles I, in dem die unabhängige Variable  variieren darf:
Zur Zeit
variieren darf:
Zur Zeit 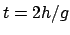 trifft die Masse
trifft die Masse  auf dem Boden auf. Für Zeiten
auf dem Boden auf. Für Zeiten
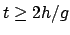 ist die Lösung:
ist die Lösung:
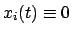 .
.
Senktechter Wurf im Schwerefeld der Erde
Kraft und Bewegungsgleichungen wie in §3.4.1; es
wirkt nur die Schwerkraft, daher auch gleiche allg. Lösung.
Die Anfangsbedingungen sind aber anders (s. Abb. 3.1):
Die spezielle Lösung ist:
Am höchsten Punkt der Bahn hat der Massenpunkt die Geschwindigkeit Null.
Bewegung eines geladenen Teilchens in einem homogenen Magnetfeld
Wir zeigen nun an zwei weiteren Beispielen die Verwendung der Formeln
(2.6) - (2.8) für
Tangential- und Normalbeschleunigung in Zusammenhang mit dem 2. Newtonschen
Axiom, Gl. (3.1).
Die Kraft, die ein magnetisches Feld auf ein bewegtes geladenes Teilchen
ausübt, heißt Lorentzkraft. Sie hat je nach Maßsystem
etwas verschiedenes Aussehen:
cgs-System:
e = Ladung des Teilchens (Elementarladung:
 cgs-Einh.),
cgs-Einh.),
c = Vakuumlichtgeschwindigkeit
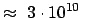 cm/s.
cm/s.
MKSA-System:
e = Ladung des Teilchens (Elementarladung:
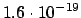 Cb),
Cb),
![$ [e] = As = Cb$](img272.gif) ;
;
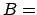 magnetische Induktion,
magnetische Induktion,
![$ [B] = T = Vs/m^{2}$](img274.gif) .
.
![$\displaystyle \vec F_L = e[\vec v, \vec B] .$](img275.gif) |
(310) |
Dieses Gesetz stammt aus der Erfahrung: Kraft auf stromdurchflossenen Leiter
im Magnetfeld, bewegte Ladung = Strom. Aus der Bewegungsgleichung (3.11) wird
berechnet:
![$\displaystyle m \vec{b} = \vec{F_{L}} = e [ \vec{v}, \vec{B} ] \Big\vert \cdot \vec{v},$](img276.gif) |
(311) |
Ein Magnetfeld kann den absoluten Betrag der Geschwindigkeit nicht ändern,
sondern nur deren Richtung. Dies ist eine Folge davon, daß die Kraft auf der
Geschwindigkeit senkrecht steht. Da die Kraft auch senkrecht zum Magnetfeld
steht, ist die Geschwindigkeit in Richtung des Magnetfeldes konstant:
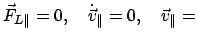
const.
(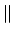 = parallel zum Magnetfeld). Aus (2.6) - (2.8) und
(3.1) folgt mit (3.12)
Ist das Magnetfeld homogen,
= parallel zum Magnetfeld). Aus (2.6) - (2.8) und
(3.1) folgt mit (3.12)
Ist das Magnetfeld homogen, 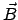 = const., und steht die
Anfangsgeschwindigkeit des Teilchens senkrecht zum Magnetfeld, dann ist
= const., und steht die
Anfangsgeschwindigkeit des Teilchens senkrecht zum Magnetfeld, dann ist
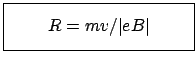 |
(313) |
Die Bahn ist ein Kreis mit Radius 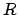 . Erfolgt der Einschuß nicht senkrecht zu
. Erfolgt der Einschuß nicht senkrecht zu
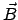 , dann ist die Bahn eine Schraube auf einem Zylinder vom Radius
, dann ist die Bahn eine Schraube auf einem Zylinder vom Radius
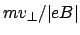 .
Obige Rechnungen sind nichtrelativistisch, nur gültig für
.
Obige Rechnungen sind nichtrelativistisch, nur gültig für
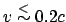 .
.
Zahlenbeispiele:
- Protonenzyklotron:
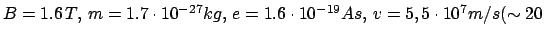 MeV Protonen):
MeV Protonen):
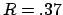 m.
m.
- Proton im Magnetfeld der Erde:
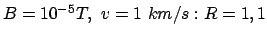 m .
m .
Das mathematische Pendel
Das mathematische Pendel (E.: mathematical pendulum) besteht aus einer
punktförmigen Masse  an einer gewichtslosen Stange der Länge
an einer gewichtslosen Stange der Länge 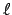 , die
in einer Ebene schwingen kann (Abb. 3.2).
Die Newtonsche Bewegungsgleichung wird in eine Normalkomponente in Richtung
der Stange und in eine Tangentialkomponente senkrecht dazu zerlegt. Eine
Bewegung in der Normalenrichtung ist durch die Starrheit der Stange unmöglich.
, die
in einer Ebene schwingen kann (Abb. 3.2).
Die Newtonsche Bewegungsgleichung wird in eine Normalkomponente in Richtung
der Stange und in eine Tangentialkomponente senkrecht dazu zerlegt. Eine
Bewegung in der Normalenrichtung ist durch die Starrheit der Stange unmöglich.
Abbildung 3.2:
Das mathematische Pendel.
|
|
Für die tangentielle Beschleunigung und Kraft erhält man:
Die exakte Bewegungsgleichung lautet also:
 |
(314) |
Diese Gleichung läßt sich exakt lösen; dies ist aber etwas kompliziert und
erfolgt erst später. Hier nur eine Näherung für kleine Schwingungen. Dann geht
Gl. (3.14) in die gewöhnliche Schwingungsgleichung über, deren allgemeine
Lösung man sofort angeben kann.
Für den Maximalausschlag
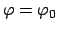 als Anfangsbedingung
erhält man die spezielle Lösung:
als Anfangsbedingung
erhält man die spezielle Lösung:
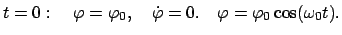 |
(315) |
Das Pendel schwingt zwischen
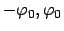 mit der
Schwingungsdauer
mit der
Schwingungsdauer 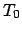 :
:
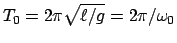 |
(316) |
Die exakte Lösung der Bewegungsgleichung (3.14) mittels elliptischer Integrale
und Funktionen erfolgt in §6.3.3.
Die Lösung der Newtonschen Bewegungsgleichung erfordert die Lösung eines
oft komplizierten Differentialgleichungssystems. In diesem Paragraphen werden
einige allgemeine Methoden behandelt, die es gestatten, für gewisse Typen von
Kräften die Bewegungsgleichung wenigstens teilweise zu integrieren. Dabei
ergeben sich gewisse dynamische Größen, wie z.B. Gesamtenergie oder Drehimpuls,
die in bestimmten Typen von Kraftfeldern unverändert (= zeitlich konstant)
bleiben. Diese Größen heißen dann Konstante oder Integrale der Bewegung
(E.: constants or integrals of the motion) oder
Erhaltungsgrößen (E.: conserved quantities). Die Bedingungen, die das
Kraftfeld erfüllen muß, damit
eine solche Größe erhalten bleibt, werden in Erhaltungssätzen (E. conservation
theorems) formuliert. Der wesentliche mathematische Gesichtspunkt besteht darin, die
Bewegungsgleichungen derart umzuformen, daß man eine totale Zeitableitung herausziehen
kann.
Die Newtonsche Bewegungsgleichung (3.1) läßt sich auch schreiben als:
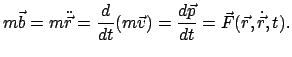 |
(317) |
Hier wurde eine neue Größe eingeführt, der Impuls oder die
Bewegungsgröße:
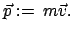 |
(318) |
Der Impuls ist ein Maß für die ''Bewegtheit'' eines Teilchens. Gl. (3.17) besagt:
Die Kraft bewirkt die Änderung des Impulses. Ist keine Kraft vorhanden, dann
bleibt der Impuls konstant, der Massenpunkt führt eine gleichförmig
geradlinige Bewegung aus; es gilt der Erhaltungssatz des Impulses
(E.: conservation of linear momentum):
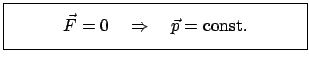 |
(319) |
Integriert man Gl. (3.17) längs der Teilchenbahn  , gilt:
, gilt:
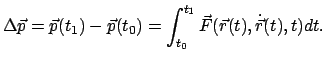 |
(320) |
Das Integral auf der rechten Seite heißt der Kraftstoß
(E.: impulse); dieser bewirkt die
Impulsänderung. Das Integral kann man aber nur berechnen, wenn man bereits die
Bahn  kennt, also bereits das Problem vollständig gelöst hat. Eine
näherungsweise Auswertung ist möglich, wenn das Zeitintervall
kennt, also bereits das Problem vollständig gelöst hat. Eine
näherungsweise Auswertung ist möglich, wenn das Zeitintervall
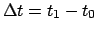 genügend kurz ist, sodaß die Kraft als konstant approximiert werden kann:
genügend kurz ist, sodaß die Kraft als konstant approximiert werden kann:
Abbildung:
a) Arbeit längs geradem Weg, b) Linienintegral für gekrümmten Weg.
|
[]
![\includegraphics[scale=0.85]{k3_arbeit}](img313.gif) []
[]
![\includegraphics[scale=0.75]{k3_linieninteg}](img314.gif) |
Die Newtonsche Bewegungsgleichung (3.1) wird skalar mit der Geschwindigkeit
 multipliziert und anschließend nach der Zeit integriert:
multipliziert und anschließend nach der Zeit integriert:
Das Integral auf der rechten Seite
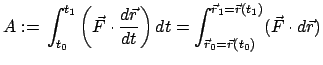 |
(321) |
gibt die Arbeit (E.: work), die die Kraft am Massenpunkt leistet (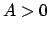 ) oder aus diesem
gewinnt (
) oder aus diesem
gewinnt (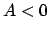 ). Bei einem kleinen geradlinigen Wegstück
). Bei einem kleinen geradlinigen Wegstück
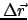 projiziert das
innere Produkt den Kraftvektor auf den Weg (Abb. 3.3):
Ist der Weg keine Gerade, dann ist die Arbeit das Linienintegral (3.21), in dem
jeweils das Wegelement
projiziert das
innere Produkt den Kraftvektor auf den Weg (Abb. 3.3):
Ist der Weg keine Gerade, dann ist die Arbeit das Linienintegral (3.21), in dem
jeweils das Wegelement 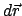 skalar mit dem zugehörigen Wert der Kraft
multipliziert wird. Beachte, daß man im allg. den Weg
skalar mit dem zugehörigen Wert der Kraft
multipliziert wird. Beachte, daß man im allg. den Weg  angeben
muß, längs dem
die Integrationskurve von
angeben
muß, längs dem
die Integrationskurve von
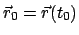 nach
nach
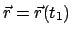 läuft.
läuft.
Die kinetische Energie (E.: kinetic energy) wird definiert als:
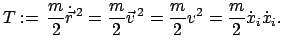 |
(322) |
Aus der obigen Gleichung folgt dann: Die Änderung der kinetischen Energie
ist gleich der von der Kraft am Massenpunkt geleisteten Arbeit:
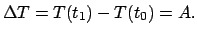 |
(323) |
Zur Berechnung der Arbeit 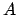 gemäß Definition (3.21) muß im allgem. wie bei
Gl. (3.20) die Bahn
gemäß Definition (3.21) muß im allgem. wie bei
Gl. (3.20) die Bahn  des Massenpunktes bekannt sein, also das Problem
gelöst
sein. Doch gibt es eine wichtige Klasse von Kräften, bei denen diese Kenntnis
nicht benötigt wird. Systeme, bei denen der Wert des Arbeitsintegrals
(3.21) unabhängig vom Weg ist, heißen konservativ (= energetisch
abgeschlossen). Das
Arbeitsintegral hängt nur vom Anfangspunkt
des Massenpunktes bekannt sein, also das Problem
gelöst
sein. Doch gibt es eine wichtige Klasse von Kräften, bei denen diese Kenntnis
nicht benötigt wird. Systeme, bei denen der Wert des Arbeitsintegrals
(3.21) unabhängig vom Weg ist, heißen konservativ (= energetisch
abgeschlossen). Das
Arbeitsintegral hängt nur vom Anfangspunkt
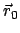 und vom Endpunkt
und vom Endpunkt
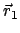 ab. Wir
setzen nun voraus, daß die Kraft
ab. Wir
setzen nun voraus, daß die Kraft 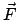 weder von der Zeit
weder von der Zeit  , noch von
der Geschwindigkeit
, noch von
der Geschwindigkeit
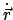 abhängt.
Konservatives System z.B.: elektrostatische Kraft, Gravitationskraft
(Abb. 3.4(a))
abhängt.
Konservatives System z.B.: elektrostatische Kraft, Gravitationskraft
(Abb. 3.4(a))
Abbildung 3.4:
a) Konservatives System b) Nichtkonservatives System
|
[]
![\includegraphics[scale=0.7]{k3_konsys}](img336.gif) []
[]
![\includegraphics[scale=0.7]{k3_nichtkonsys}](img337.gif) |
Nichtkonservatives System (Abb. 3.4(b)) z.B.: Wasserwirbel, Korkstückchen von 1 nach 2 transportiert auf verschiedenen
Wegen.
In einem konservativen System gilt also für einen geschlossenen
Integrationsweg:
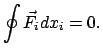 |
(324) |
Mittels des Stokesschen Integralsatzes kann man dieses Integral umformen:
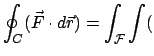
rot
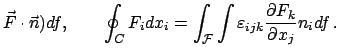
Hier ist 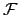 eine beliebige, von
eine beliebige, von 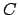 begrenzte Fläche mit dem Normalenvektor
begrenzte Fläche mit dem Normalenvektor
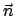 .
Da in konservativen Systemen die linke Seite Null ist und dieses Resultat für
beliebige
.
Da in konservativen Systemen die linke Seite Null ist und dieses Resultat für
beliebige 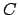 und
und 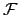 gilt, folgt
gilt, folgt
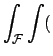 rot rot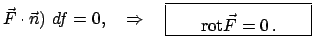 |
(325) |
d.h. daß das Kraftfeld wirbelfrei (E.: irrotational) sein muß. Der
Rotor eines
Vektorfeldes 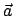 kann berechnet werden gemäß:
kann berechnet werden gemäß:
rot
![$\displaystyle \vec a(x,y,z) = \nabla \times \vec a =
\left\vert \begin{arra...
...artial}{\partial z} [1mm]
a_{x} & a_{y} & a_{z}
\end{array} \right\vert .
$](img348.gif)
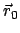 jedem Raumpunkt einen Skalar
jedem Raumpunkt einen Skalar
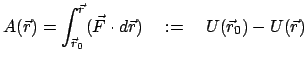 |
(326) |
zuordnen. Man normiert 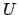 meist so, daß
meist so, daß
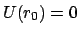 ist. Man nennt
ist. Man nennt
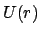 die
potentielle Energie (E.: potential energy). Dies ist die Arbeit, die nötig ist, um einen
Massenpunkt
im Kraftfeld
die
potentielle Energie (E.: potential energy). Dies ist die Arbeit, die nötig ist, um einen
Massenpunkt
im Kraftfeld 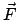 vom Punkt
vom Punkt
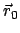 zum Punkt
zum Punkt 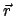 zu bringen.
Punkte gleichen Potentials
liegen meist auf einer Fläche. Diese Flächen heißen Äquipotentialflächen (E.: equipotential surfaces).
zu bringen.
Punkte gleichen Potentials
liegen meist auf einer Fläche. Diese Flächen heißen Äquipotentialflächen (E.: equipotential surfaces).
Eine Ladung 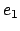 sei in
sei in
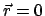 , die zweite,
, die zweite,  , in
, in 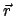 .
Gemäß dem Coulombschen Gesetz gilt für die Kraft zwischen den beiden
Ladungen: (in MKSA Maßeinheiten)
.
Gemäß dem Coulombschen Gesetz gilt für die Kraft zwischen den beiden
Ladungen: (in MKSA Maßeinheiten)
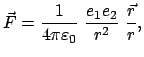 |
(327) |
rot
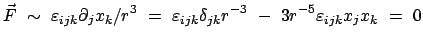
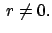
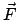 ist also wirbelfrei, es existiert ein Potential. Also
ist das Arbeitsintegral (3.24) unabhängig vom Verlauf
des Integrationsweges. Anstelle von
ist also wirbelfrei, es existiert ein Potential. Also
ist das Arbeitsintegral (3.24) unabhängig vom Verlauf
des Integrationsweges. Anstelle von 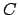 wird
wird
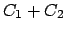 genommen (
genommen (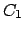 ist ein Radiusstück,
ist ein Radiusstück, 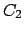 ein Kreisbogenstück, s. Abb. 3.4(a))
Es wird nun als Bezugspunkt
ein Kreisbogenstück, s. Abb. 3.4(a))
Es wird nun als Bezugspunkt
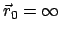 gewählt, dann ist
gewählt, dann ist
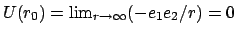 .
.
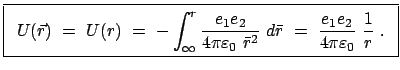 |
(328) |
Die Äquipotentialflächen sind die Kugeln  =
const. Gl. (3.27) und (3.28) gelten
auch für die Anziehung zweier Massen mit der Ersetzung
=
const. Gl. (3.27) und (3.28) gelten
auch für die Anziehung zweier Massen mit der Ersetzung
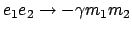 (
(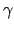 = Gravitationskonstante).
= Gravitationskonstante).
Abbildung:
a) Sphärisches elektrostatisches Kraftfeld b)
Schwerefeld
|
[]
![\includegraphics[scale=0.63]{k3_sph_e_feld}](img372.gif) []
[]
![\includegraphics[scale=0.63]{k3_schwerefeld}](img373.gif) |
Der Erdboden wird als Bezugspunkt mit 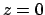 genommen (Abb. 3.5(b)).
genommen (Abb. 3.5(b)).
Die Äquipotentialflächen sind Ebenen parallel zum Erdboden. Die potentielle
Energie einer Masse ist proportional zu ihrer Höhe über dem Boden.
Kombination von Gln. (3.23) und (3.26)
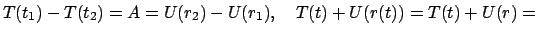
const
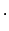
gibt den Erhaltungssatz der Gesamtenergie E (E.: conservation of total
energy): Ist ein Kraftfeld in einem Gebiet des Raumes
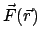
1) unabhängig von der Zeit  und von der Geschwindigkeit
und von der Geschwindigkeit
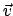 und 2) existiert dort
rot
und 2) existiert dort
rot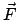 und ist dort
rot
und ist dort
rot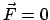 ,
dann ist die Gesamtenergie
,
dann ist die Gesamtenergie 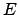 zeitlich konstant, also ein Integral der Bewegung:
zeitlich konstant, also ein Integral der Bewegung:
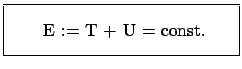 |
(330) |
Mit der Anfangsbedingung:
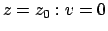 folgt aus
(3.30) (Abb. 3.6(a)):
folgt aus
(3.30) (Abb. 3.6(a)):
und die Endgeschwindigkeit des Teilchens ist:
Abbildung 3.6:
a) Ebenes elektrisches Feld im Plattenkondensator b) Allgemeines
elektrisches Feld
|
[]
![\includegraphics[scale=0.7]{k3_kondensator}](img388.gif) []
[]
![\includegraphics[scale=0.7]{k3_allg_e_feld}](img389.gif) |
Dieser Sachverhalt gilt ganz allgemein für beliebige elektrostatische Felder
(Abb. 3.6(b)): Die Änderung der kinetischen Energie ist gleich der
durchlaufenen Potentialdifferenz:
Aus einem Potential 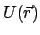 kann man das Kraftfeld berechnen gemäß
kann man das Kraftfeld berechnen gemäß
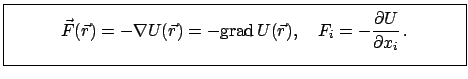 |
(331) |
Darin ist:
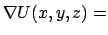 grad grad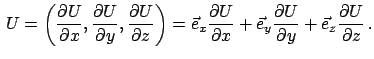 |
(332) |
Diese Formel beweist man, indem man den Nablaoperator, wie in Gl. (3.32) definiert,
auf Gl. (3.26) anwendet:
Die linke, vektorielle Formel entspricht der rechten im eindimensionalen Fall.
An jedem Punkt eines Skalarfeldes 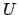 weist der Gradient in die Richtung der
größten Änderung von
weist der Gradient in die Richtung der
größten Änderung von 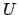 ; ebenso weist die Kraft in Richtung der stärksten
Potentialänderung (z.B. auf einem Hang in Richtung der Fallinie).
; ebenso weist die Kraft in Richtung der stärksten
Potentialänderung (z.B. auf einem Hang in Richtung der Fallinie).
Mit Gl. (3.31) kann man den Energiesatz
(3.30) aus der Newtonschen Bewegungsgleichung
(3.1) ableiten:
Ist die Kraft zeitabhängig, dann ist das System nicht konservativ.
Es kann
trotzdem möglich sein, daß man eine zeitabhängige Potentialfunktion
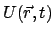 finden kann, sodaß gilt
finden kann, sodaß gilt
 |
(333) |
Diese Potentialfunktion
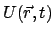 ist aber keine potentielle Energie.
Man kann
mit ihr den Ausdruck für die Gesamtenergie
ist aber keine potentielle Energie.
Man kann
mit ihr den Ausdruck für die Gesamtenergie 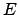 bilden, doch ist diese nicht
erhalten, d.i. nicht zeitlich konstant:
Ebenso ist im allg. ein System nicht konservativ, wenn eine
Kraft geschwindigkeitsabhängig ist.
Z.B. ergibt sich für eine Reibungskraft (E.: frictional force)
bilden, doch ist diese nicht
erhalten, d.i. nicht zeitlich konstant:
Ebenso ist im allg. ein System nicht konservativ, wenn eine
Kraft geschwindigkeitsabhängig ist.
Z.B. ergibt sich für eine Reibungskraft (E.: frictional force)
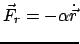 |
(334) |
aus der Newtonschen Bewegungsgleichung (3.1):
Die Gesamtenergie 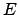 fällt hier mit der kinetischen Energie
fällt hier mit der kinetischen Energie 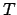 zusammen;
diese
wird durch die Reibung vermindert; die entstehende Wärme verringert die
anfänglich vorhandene Menge an mechanischer Energie.
zusammen;
diese
wird durch die Reibung vermindert; die entstehende Wärme verringert die
anfänglich vorhandene Menge an mechanischer Energie.
Eine Ausnahme bilden solche geschwindigkeitsabhängigen
Kräfte, die senkrecht zur Geschwindigkeit
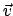 des Teilchens stehen. Diese sind konvervativ, doch existiert
kein Potential, sondern nur ein verallgemeinertes Potential (s. Kap.11 ).
Z.B. gilt für die Lorentzkraft,
des Teilchens stehen. Diese sind konvervativ, doch existiert
kein Potential, sondern nur ein verallgemeinertes Potential (s. Kap.11 ).
Z.B. gilt für die Lorentzkraft,
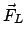 , Gl. (3.11):
, Gl. (3.11):
Dieses Beispiel zeigt, daß ein System bereits durch einen einzigen singulären
Punkt nichtkonservativ gemacht werden kann. Das
Kraftfeld 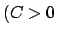 ist eine Konstante, deren Wert hier unwichtig ist)
ist zweidimensional. Es gilt für
ist eine Konstante, deren Wert hier unwichtig ist)
ist zweidimensional. Es gilt für
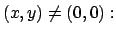 rot
rot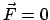 (Nachrechnen !).
An
(Nachrechnen !).
An
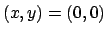 sind
sind 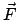 und
rot
und
rot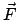 singulär. Diese Singularität
der Kraft stellt
einen Wirbel dar. Denn das Arbeitsintegral längs eines Kreises um (0,0) hat
(unabhängig von dessen Radius
singulär. Diese Singularität
der Kraft stellt
einen Wirbel dar. Denn das Arbeitsintegral längs eines Kreises um (0,0) hat
(unabhängig von dessen Radius 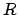 ) den Wert
) den Wert 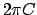 . Dies berechnet man,
indem man von
. Dies berechnet man,
indem man von 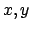 auf Polarkoordinaten übergeht:
auf Polarkoordinaten übergeht:
Man sieht, daß
rot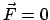 in allen Punkten eines Gebietes erfüllt
sein muß, damit das Kraftfeld
in allen Punkten eines Gebietes erfüllt
sein muß, damit das Kraftfeld 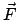 darin wirbelfrei ist. In einem einfach
zusammenhängenden Gebiet, das
darin wirbelfrei ist. In einem einfach
zusammenhängenden Gebiet, das 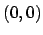 nicht einschließt oder berührt,
existiert für obige Kraft ein Potential:
nicht einschließt oder berührt,
existiert für obige Kraft ein Potential:
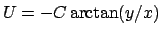 . In einem
Ringbereich in dessen Zentrum, das nicht zum Bereich gehört,
. In einem
Ringbereich in dessen Zentrum, das nicht zum Bereich gehört, 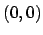 liegt, ist
diese Funktion mehrdeutig, damit kein Potential.
liegt, ist
diese Funktion mehrdeutig, damit kein Potential.
Drehimpuls und Drehmoment
Man bildet das äußere Produkt des Ortsvektors mit der Bewegungsgleichung (3.1)
und erhält wegen
die Gleichung
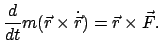 |
(335) |
Durch das Vektorprodukt mit 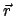 holt man aus der Newtonschen Bewegungsgleichung
einen Drehanteil heraus. Die in Gl. (3.35) auftretenden
Größen werden in Definitionen erfaßt. Der Drehimpuls (E.: angular
momentum, moment of momentum):
holt man aus der Newtonschen Bewegungsgleichung
einen Drehanteil heraus. Die in Gl. (3.35) auftretenden
Größen werden in Definitionen erfaßt. Der Drehimpuls (E.: angular
momentum, moment of momentum):
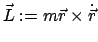 |
(336) |
ist ein Maß für die Drehbewegung der Masse  (mit Lage
(mit Lage 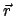 ) um den
Ursprung (Abb. 3.7(a)). Das Drehmoment (E.:
torque, moment of force):
) um den
Ursprung (Abb. 3.7(a)). Das Drehmoment (E.:
torque, moment of force):
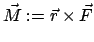 |
(337) |
ist ein Maß für die Drehwirkung der Kraft
(Abb. 3.7(b)). Der Betrag von Gl. (3.37) gibt:
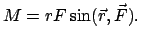 |
(338) |
Diese Gleichung zeigt, daß nur die zu 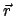 senkrechte Komponente der Kraft
senkrechte Komponente der Kraft
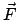 zum Drehmoment beiträgt.
zum Drehmoment beiträgt.
Abbildung 3.7:
a) Vektorprodukt des Drehimpulses b) Vektorprodukt des Drehmoments
|
[]
![\includegraphics[scale=0.7]{k3_vecprod_drehimp}](img421.gif) []
[]
![\includegraphics[scale=0.7]{k3_vecprod_drehmom}](img422.gif) |
Mit Gln. (3.36) und (3.37) wird Gl. (3.38) neu geschrieben:
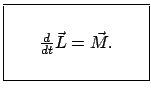 |
(339) |
Die Änderung des Drehimpulses ist gleich dem Drehmoment der Kraft. Wenn das
Drehmoment Null ist, gilt der Erhaltungssatz des Drehimpulses (E.:
conservation of angular momentum):
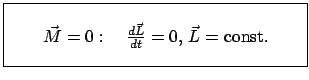 |
(340) |
Der Drehimpuls ist in diesem Fall ein zeitlich konstanter Vektor; er ändert
sich nicht während der Bewegung des Massenpunktes. Aus der Konstanz des
Drehimpulses folgt:
- Die Bewegung ist eben. Gemäß der Definition (3.36) des Drehimpulses
stehen
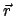 und
und
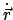 immer senkrecht zu
immer senkrecht zu 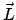 . Wenn
. Wenn 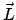 fix
ist, liegen
fix
ist, liegen 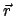 und
und
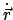 immer in der fixen
zu
immer in der fixen
zu 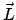 senkrechten Bahnebene.
senkrechten Bahnebene.
- Der Flächensatz: Der Fahrstrahl vom Kraftzentrum (= Ursprung)
zum Massenpunkt überstreicht in gleichen Zeiten gleiche Flächen (Abb. 3.8).
Die Fläche des vom Fahrstrahl in der Zeit
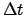 überstrichenen
Dreiecks ist:
überstrichenen
Dreiecks ist:
Abbildung:
Der Flächensatz
|
![\includegraphics[scale=0.7]{k3_flaechensatz}](img427.gif) |
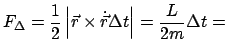 const. const. |
(341) |
Der Drehimpuls ist erhalten, wenn das Drehmoment Null ist. Dafür gibt es zwei
Möglichkeiten:
Eine wichtige Klasse von Kräften, die die zweite Bedingung erfüllt, sind die
Zentralkräfte:
Die Funktion  darf nur vom Betrag
darf nur vom Betrag  abhängen, nicht aber von den
einzelnen
Komponenten des Radiusvektors. Eine derartige Kraft besitzt immer ein Potential;
dieses ist radialsymmetrisch, nur eine Funktion von
abhängen, nicht aber von den
einzelnen
Komponenten des Radiusvektors. Eine derartige Kraft besitzt immer ein Potential;
dieses ist radialsymmetrisch, nur eine Funktion von  :
:
Es besteht ein inniger Zusammenhang zwischen der Radialsymmetrie und der
Erhaltung des Drehimpulsvektors; die eine bedingt die andere; nicht
aber umgekehrt. Dies
wird später noch bewiesen werden. Dieser Zusammenhang gilt auch bei geringerer
Symmetrie: Ist das Potential achsialsymmetrisch, dann ist die Komponente des
Drehimpulses längs dieser Achse erhalten.
Integrale der Bewegung
Eine Erhaltungsgröße (= Integral oder
Konstante der Bewegung) ist eine
Funktion der Koordinaten, Geschwindigkeiten und der Zeit, die längs der Bahn
des Teilchens konstant ist:
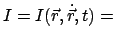 const. const.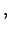 |
(342) |
wenn für 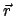 bzw.
bzw.
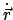 die analytischen Ausdrücke für die
Bahn
die analytischen Ausdrücke für die
Bahn  bzw. deren
Ableitungen eingesetzt werden. Kommt im Ausdruck (3.42) die Zeit
bzw. deren
Ableitungen eingesetzt werden. Kommt im Ausdruck (3.42) die Zeit  nicht
explizit vor
vor, dann heißt
nicht
explizit vor
vor, dann heißt
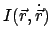 ein zeitfreies Integral der
Bewegung. Um die Konstanz
einer Größe
ein zeitfreies Integral der
Bewegung. Um die Konstanz
einer Größe 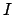 zu beweisen, ist es nicht nötig, die Lösung
zu beweisen, ist es nicht nötig, die Lösung  zu kennen.
Bildet man die totale Zeitableitung von Gl. (3.42) und setzt die Newtonsche
Bewegungsgleichung (3.1) ein, findet man
zu kennen.
Bildet man die totale Zeitableitung von Gl. (3.42) und setzt die Newtonsche
Bewegungsgleichung (3.1) ein, findet man
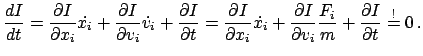 |
(343) |
Die in den vorhergehenden Paragraphen gegebenen Beweise für die
Erhaltungssätze des Impulses, der Energie und des Drehimpulses sind zu
Gl. (3.43) äquivalent. Die Erhaltung der
vorgenannten Größen ist bedingt durch grundlegende
Symmetrien der Raum-Zeit, die auch in der Newtonschen Bewegungsgleichung wirksam
werden. Die Impulserhaltung resultiert aus der Homogenität des kräftefreien
Raumes, die Energiegerhaltung aus der Homogenität der Zeit, die
Drehimpulserhaltung aus der sphärischen Symmetrie der Zentralkraft. Weitere
Integrale der Bewegung gibt es nur für spezielle Kräfte; z.B. den Laplace-Lenzschen Vektor
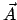 beim Keplerproblem, die Vektoren
beim Keplerproblem, die Vektoren 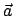 und
und 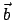 für die Halbachsen
der Bahnellipse im
linearen Zentralkraftfeld, den Poincaréschen Vektor für die Lorentzkraft
im Feld eines einzelnen (hypothetischen) Magnetpoles (s. Ü5 zu Kap. 5).
für die Halbachsen
der Bahnellipse im
linearen Zentralkraftfeld, den Poincaréschen Vektor für die Lorentzkraft
im Feld eines einzelnen (hypothetischen) Magnetpoles (s. Ü5 zu Kap. 5).
Integrale der Bewegung sind sehr nützlich für die Lösung eines mechanischen
Problems. Sie ermöglichen es, die Zahl der abhängigen Variablen und damit die Zahl der
Differentialgleichungen zu erniedrigen. Im günstigsten Fall ist mit ihrer Hilfe
das Problem vollständig gelöst. Hiezu der folgende
Satz 1:
Kennt man zu einem mechanischen Problem (eines Massenpunktes im
dreidimensionalen Raum) 5 zeitfreie Integrale der Bewegung, dann ist die
Gestalt der Bahn gefunden. Denn die Unabhängigkeit der Integrale
bedeutet, daß die Funktionaldeterminante der 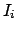 nach 5 der Variablen
nach 5 der Variablen
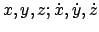 ungleich Null ist. Das ist aber auch die
Bedingung, daß
man die obigen 5 Gleichungen nach diesen 5 Variablen auflösen kann.
Eine der Variablen verbleibt als Parameter, z.B. z
ungleich Null ist. Das ist aber auch die
Bedingung, daß
man die obigen 5 Gleichungen nach diesen 5 Variablen auflösen kann.
Eine der Variablen verbleibt als Parameter, z.B. z
Diesen Satz werden wir bei der Lösung des Keplerproblems benützen.
Analog gilt der
Satz 2:
Kennt man 6 unabhängige, zeitabhängige Integrale der Bewegung,
dann ist das mechanische Problem vollständig gelöst.
Für die Bewegung eines Teilchens im dreidimensionalen Raum gibt es
immer 6 unabhängige Integrale der Bewegung, z.B. die Anfangslage
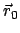 und die -geschwindigkeit
und die -geschwindigkeit
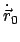 . Leitet man die Lösung des
Problems zu diesen Anfangsdaten nach der Geschwindigkeit ab, erhält man:
. Leitet man die Lösung des
Problems zu diesen Anfangsdaten nach der Geschwindigkeit ab, erhält man:
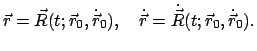 |
(344) |
Löst man dieses System von 6 unabhängigen Gleichungen nach den 6 Größen
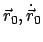 auf (dies ist im Prinzip immer möglich), dann
bekommt man die 6 Erhaltungsgrößen
auf (dies ist im Prinzip immer möglich), dann
bekommt man die 6 Erhaltungsgrößen
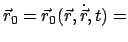
const.
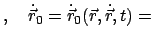
const.
Dieser Auflösungsprozess kann dynamisch auch so dargestellt werden: Vom Zeitpunkt
 läßt man das System mit umgekehrter Geschwindigkeit zurücklaufen:
Weitere Erhaltungsgrößen, wie z.B. die Energie oder der Drehimpuls hängen
von den vorgenannten ab. Aber die Anfangslage und -geschwindigkeit sind
''uninteressante'' Erhaltungsgrößen, sie ermöglichen keine allgemeinen
Aussagen
über die Bewegung. Im Gegensatz dazu sind Drehimpuls, Gesamtenergie und die
anderen im ersten Absatz dieses Paragraphen genannten Erhaltungsgrößen
''interessant'', denn sie gestatten allgemeine Aussagen über die Bewegung und
sie schränken in vielen Fällen die Bewegung des Massenpunktes ein. Z.B. die
Drehimpulserhaltung bedingt die Ebenheit der Bewegung und den Flächensatz,
der Energiesatz eines gebundenen Teilchens verbietet die Entfernung ins
Unendliche. Solche interessante Erhaltungsgrößen heißen isolierende
Integrale (E.: isolating integrals)
der Bewegung und hängen mit der Symmetrie des Kraftfeldes zusammen. Solche
isolierende Integrale der Bewegung sind auch von großer Bedeutung für die
statistische Mechanik, weil im allg. die Verteilungsfunktion, die den Zustand
eines Systems von vielen Teilchen beschreibt, nur von solchen isolierenden
Integralen abhängen kann.
läßt man das System mit umgekehrter Geschwindigkeit zurücklaufen:
Weitere Erhaltungsgrößen, wie z.B. die Energie oder der Drehimpuls hängen
von den vorgenannten ab. Aber die Anfangslage und -geschwindigkeit sind
''uninteressante'' Erhaltungsgrößen, sie ermöglichen keine allgemeinen
Aussagen
über die Bewegung. Im Gegensatz dazu sind Drehimpuls, Gesamtenergie und die
anderen im ersten Absatz dieses Paragraphen genannten Erhaltungsgrößen
''interessant'', denn sie gestatten allgemeine Aussagen über die Bewegung und
sie schränken in vielen Fällen die Bewegung des Massenpunktes ein. Z.B. die
Drehimpulserhaltung bedingt die Ebenheit der Bewegung und den Flächensatz,
der Energiesatz eines gebundenen Teilchens verbietet die Entfernung ins
Unendliche. Solche interessante Erhaltungsgrößen heißen isolierende
Integrale (E.: isolating integrals)
der Bewegung und hängen mit der Symmetrie des Kraftfeldes zusammen. Solche
isolierende Integrale der Bewegung sind auch von großer Bedeutung für die
statistische Mechanik, weil im allg. die Verteilungsfunktion, die den Zustand
eines Systems von vielen Teilchen beschreibt, nur von solchen isolierenden
Integralen abhängen kann.
Die Bewegung eines Massenpunktes kann man sich als eine Kurve im Raum der Koordinaten
vorstellen. Hat das Teilchen 2 Freiheitsgrade, dann ist das eine Kurve in einer
Ebene; bei 3 Freiheitsgraden eine Kurve im dreidimensionalen Raum. Aber derartige
Kurven können nicht alle Informationen wiedergeben, die zu einer vollständigen
Beschreibung einer Bahn gehören; denn es ist nicht ersichtich, mit welcher
Geschwindigkeit der Massenpunkt der Kurve im Ortsraum entlangläuft.
Für Darstellungen, die eine vollständige Beschreibung der Bahn liefern, verwendet man
den Phasenraum (E.: phase space); dieser wird von allen Lagekoordinaten und allen
Geschwindigkeiten aufgespannt. Bei einem Freiheitsgrad (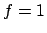 ) ist dieser Phasenraum
zweidimensional, z.B.
) ist dieser Phasenraum
zweidimensional, z.B.
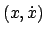 , also eine Ebene. Bei 2 Freiheitsgraden ist der Phasenraum
vierdimensional, bei 3 sechsdimensional,..., allgemein 2f-dimensional. Da man einen
vier- oder noch höherdimensionalen Raum nicht darstellen kann, muß man sich leider meist
mit Projektionen dieses Raumes begenügen. Trotzdem geben diese Darstellungen oft sehr
nützliche Einsichten und werden häufig verwendet. Diese wird in den nachfolgenden
Kapiteln gezeigt werden.
, also eine Ebene. Bei 2 Freiheitsgraden ist der Phasenraum
vierdimensional, bei 3 sechsdimensional,..., allgemein 2f-dimensional. Da man einen
vier- oder noch höherdimensionalen Raum nicht darstellen kann, muß man sich leider meist
mit Projektionen dieses Raumes begenügen. Trotzdem geben diese Darstellungen oft sehr
nützliche Einsichten und werden häufig verwendet. Diese wird in den nachfolgenden
Kapiteln gezeigt werden.
Die Lösungen (3.44)
sind Raumkurven im Phasenraum. Jedem Zeitpunkt  entspricht ein Punkt dieser Kurve;
dessen
entspricht ein Punkt dieser Kurve;
dessen 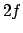 Koordinaten geben die zu diesem Zeitpunkt vom Massenpunkt angenommene
Lagekoordinaten und Geschwindigkeiten an. Man nennt daher diese Raumkurve im
Koordinaten geben die zu diesem Zeitpunkt vom Massenpunkt angenommene
Lagekoordinaten und Geschwindigkeiten an. Man nennt daher diese Raumkurve im
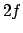 -dimensionalen Phasenraum Phasenkurve (E.: trajectory in phase space).
Wenn sich der Massenpunkt im Laufe der Zeit bewegt, dann ensprechen aufeinerfolgende Punkte der
Phasenkurve seinen aufeinanderfolgenden Zuständen. Den Punkt der auf der Kurve den momentanen
Zustand des Massenpunkts beschreibt, nennt man Phasenpunkt (E.: phase point). Während der
Bewegung des Massenpunktes läuft er auf der Phasenkurve dahin.
-dimensionalen Phasenraum Phasenkurve (E.: trajectory in phase space).
Wenn sich der Massenpunkt im Laufe der Zeit bewegt, dann ensprechen aufeinerfolgende Punkte der
Phasenkurve seinen aufeinanderfolgenden Zuständen. Den Punkt der auf der Kurve den momentanen
Zustand des Massenpunkts beschreibt, nennt man Phasenpunkt (E.: phase point). Während der
Bewegung des Massenpunktes läuft er auf der Phasenkurve dahin.
Ein zeitfreies Integral der Bewegung ist eine Funktion der Lagekoordinaten und
Geschwindigkeiten:
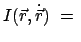
const.
Es gibt eine Hyperfläche im Phasenraum. Der Phasenpunkt verbleibt während der
ganzen Bewegung auf dieser; mit anderen Worten: die Phasenkurve liegt in dieser
Fläche. Gibt es weitere unabhängige zeitfreie Integrale der Bewegung, dann
kann die Phasenkurve nur im Durchschnitt all dieser Flächen liegen.
Die Bewegungsmöglichkeiten des Phasenpunktes, damit auch des realen Massenpunktes,
werden damit mehr oder weniger eingeschränkt. Daraus ist auch ersichtlich, daß
es maximal 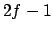 zeitfreie Integrale der Bewegung geben kann. Denn die zugehörigen
Flächen schneiden sich dann gerade in einer Kurve, der Phasenkurve. Gäbe es
ein weiteres unabhängiges zeitfreies Integral, dann würde die zugehörige Fläche
die Phasenbahn in einem Punkt (oder vielleicht eine diskrete Menge von solchen)
schneiden; der Phasenpunkt wäre fixiert, der reale Massenpunkt unbeweglich.
zeitfreie Integrale der Bewegung geben kann. Denn die zugehörigen
Flächen schneiden sich dann gerade in einer Kurve, der Phasenkurve. Gäbe es
ein weiteres unabhängiges zeitfreies Integral, dann würde die zugehörige Fläche
die Phasenbahn in einem Punkt (oder vielleicht eine diskrete Menge von solchen)
schneiden; der Phasenpunkt wäre fixiert, der reale Massenpunkt unbeweglich.
Bei isolierenden Integralen der Bewegung ist die zugehörige Fläche im Phasenraum
'' verhältnismäßig einfach '' . Oft schränkt ein solches die Beweglichkeit des
Phasenpunktes auf Teilgebiete des Phasenraumes ein. Auch die Bewegung des realen
Massenpunkts muß dann einfacher und übersichtlicher sein. Bei nichtisolierenden
Integralen der Bewegung können diese Flächen wild oszillieren und vielfach
zusammenhängen. Dann ist ihre Wirksamkeit als '' Käfig '' für den Phasenpunkt sehr
gering oder nicht existent.
Eine Einsicht über das Vorhandensein von Integralen der Bewegung liefert die
von den berühmten französischen Mathematiker erfundene und nach ihm benannte
Poincaré-Abbildung. Diese erhält man, indem man im Phasenraum eine
geeignete Ebene auswählt und die Punkte einzeichnet, in denen die Phasenkurve
die Ebene durchstößt. Sind Integrale der Bewegung vorhanden, dann bilden die
Phasenpunkte ein regelmäßiges Muster, liegen oft auf einer Kurve. Liegt kein
(oder fast kein) Integral der Bewegung vor, dann ist die Bewegung chaotisch und
die Durchstoßpunkte verteilen sich regellos über die Ebene.
Dies alles wird in den nächsten Kapiteln an einigen Beispielen erklärt werden.
Man kann auch die Impulskomponenten statt der Geschwindigkeitskomponenten als
Koordinaten des Phasenraumes heranziehen. In den meisten Fällen gibt dies nur
einen unwesentlichen Unterschied, da sich die beiden Größen nur um die konstante
Masse unterscheiden. Im 12. Kapitel wird dann der
kanonische Impuls eingeführt
werden; dieser ist nicht immer gleich dem gewöhnlichen oder linearen Impuls wie
er in diesem Kapitel definiert worden ist. Z.B. bei geschwindigkeitsabhängigen
Kräften unterscheidet sich der lineare Impuls (proportional zur Geschwindigkeit)
vom kanonischen. Der eigentliche Phasenraum wird mittels des kanonischen Impulses
definiert; für manche Untersuchungen kann es aber zweckmäßiger sein, die
Geschwindigkeitskomponenten statt der des kanonischen Impulses zu verwenden.
Christian Sommer
2003-01-27
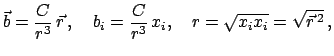
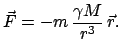
![]() , die an einem Körper wirkt, wenn die Umstände
für das
Auftreten der einzelnen Kräfte
, die an einem Körper wirkt, wenn die Umstände
für das
Auftreten der einzelnen Kräfte
![]() zugleich
vorliegen, ist gleich
zugleich
vorliegen, ist gleich
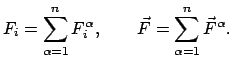
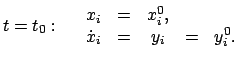
![]() )-dimensionalen Bereich um
)-dimensionalen Bereich um
![]() seien
seien
![]() (i = 1,...,f) erfüllen als lineare Gleichungen die Bedingungen
(3.7) und (3.8) in trivialer Weise. Aus
(3.5), (3.6b) und (3.7) folgt:
(i = 1,...,f) erfüllen als lineare Gleichungen die Bedingungen
(3.7) und (3.8) in trivialer Weise. Aus
(3.5), (3.6b) und (3.7) folgt:
![]() befindet sich im Schwerefeld in der Höhe
befindet sich im Schwerefeld in der Höhe ![]() über dem Boden
(Abb. 3.1(a) ). Es ist zweckmäßig, das Koordinatensystem so zu legen, wie in
Abb. 3.1(b) gezeigt. Die Kraft ist dann:
über dem Boden
(Abb. 3.1(a) ). Es ist zweckmäßig, das Koordinatensystem so zu legen, wie in
Abb. 3.1(b) gezeigt. Die Kraft ist dann:
![\includegraphics[width=15cm]{SK3A1}](img249.gif)
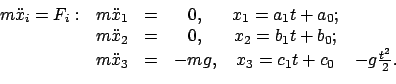
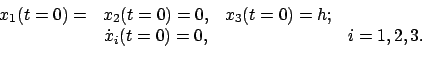
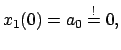
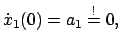
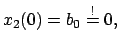
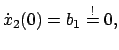
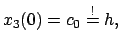
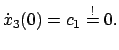
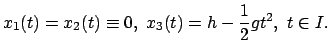
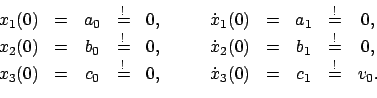
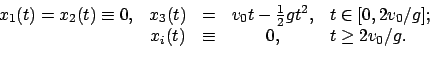
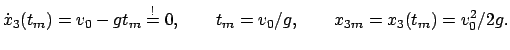
![]() cgs-Einh.),
cgs-Einh.),
![]() cm/s.
cm/s.
![$\displaystyle m(\vec v,\dot{\vec v}) = \frac{d}{dt} \frac{m}{2} v^{2} = e \vec v \cdot [\vec v,
\vec B] = 0,
$](img277.gif)
![$\displaystyle m \vec b = m \underbrace{\dot{v}}_{= 0} \vec e_{t} - m \frac{v^2}{R} \vec e_{n} =
e[\vec v,\vec B] .
$](img283.gif)
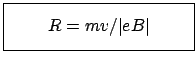
![]() an einer gewichtslosen Stange der Länge
an einer gewichtslosen Stange der Länge ![]() , die
in einer Ebene schwingen kann (Abb. 3.2).
Die Newtonsche Bewegungsgleichung wird in eine Normalkomponente in Richtung
der Stange und in eine Tangentialkomponente senkrecht dazu zerlegt. Eine
Bewegung in der Normalenrichtung ist durch die Starrheit der Stange unmöglich.
, die
in einer Ebene schwingen kann (Abb. 3.2).
Die Newtonsche Bewegungsgleichung wird in eine Normalkomponente in Richtung
der Stange und in eine Tangentialkomponente senkrecht dazu zerlegt. Eine
Bewegung in der Normalenrichtung ist durch die Starrheit der Stange unmöglich.
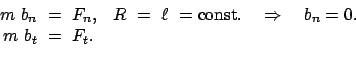
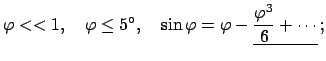
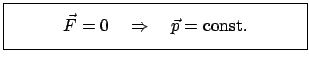
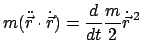
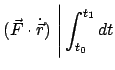
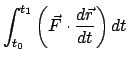
![\begin{displaymath}
\begin{array}{ccc}
\int_{C_{1}} F_{i} d x_{i} & = & \int_{...
...[2mm]
\int_{C_{1}-C_{2}} F_{i} dx_{i} & = & 0.
\end{array}\end{displaymath}](img335.gif)
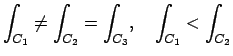
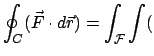 rot
rot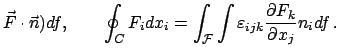
![$\displaystyle \vec a(x,y,z) = \nabla \times \vec a =
\left\vert \begin{arra...
...artial}{\partial z} [1mm]
a_{x} & a_{y} & a_{z}
\end{array} \right\vert .
$](img348.gif)
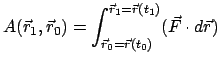
![]() sei in
sei in
![]() , die zweite,
, die zweite, ![]() , in
, in ![]() .
Gemäß dem Coulombschen Gesetz gilt für die Kraft zwischen den beiden
Ladungen: (in MKSA Maßeinheiten)
.
Gemäß dem Coulombschen Gesetz gilt für die Kraft zwischen den beiden
Ladungen: (in MKSA Maßeinheiten)
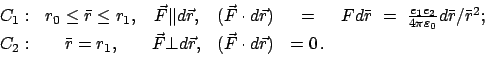
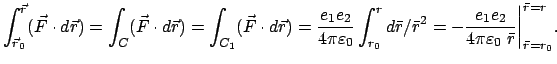
![]() =
const. Gl. (3.27) und (3.28) gelten
auch für die Anziehung zweier Massen mit der Ersetzung
=
const. Gl. (3.27) und (3.28) gelten
auch für die Anziehung zweier Massen mit der Ersetzung
![]() (
(![]() = Gravitationskonstante).
= Gravitationskonstante).
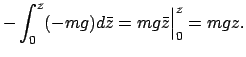
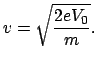
![\includegraphics[scale=0.7]{k3_kondensator}](img388.gif) []
[]
![\includegraphics[scale=0.7]{k3_allg_e_feld}](img389.gif)
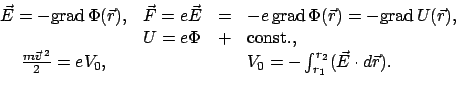
![]() kann man das Kraftfeld berechnen gemäß
kann man das Kraftfeld berechnen gemäß
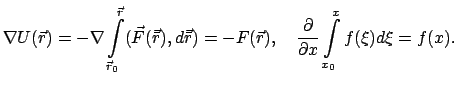
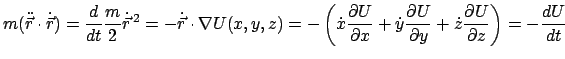
![]() finden kann, sodaß gilt
finden kann, sodaß gilt
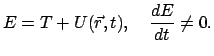
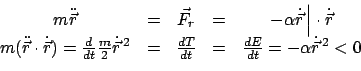
![]() fällt hier mit der kinetischen Energie
fällt hier mit der kinetischen Energie ![]() zusammen;
diese
wird durch die Reibung vermindert; die entstehende Wärme verringert die
anfänglich vorhandene Menge an mechanischer Energie.
zusammen;
diese
wird durch die Reibung vermindert; die entstehende Wärme verringert die
anfänglich vorhandene Menge an mechanischer Energie.
![]() des Teilchens stehen. Diese sind konvervativ, doch existiert
kein Potential, sondern nur ein verallgemeinertes Potential (s. Kap.11 ).
Z.B. gilt für die Lorentzkraft,
des Teilchens stehen. Diese sind konvervativ, doch existiert
kein Potential, sondern nur ein verallgemeinertes Potential (s. Kap.11 ).
Z.B. gilt für die Lorentzkraft,
![]() , Gl. (3.11):
, Gl. (3.11):
![$\displaystyle m \ddot{\vec r} = \vec F_{L} = e [\dot {\vec r} \times \vec B] ...
... (\frac{m}{2} \dot{\vec r}^{ 2}
\right ) =
\frac{dT}{dt} = \frac{dE}{dt} = 0.
$](img405.gif)
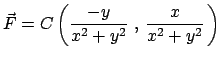
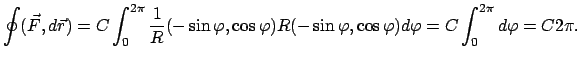
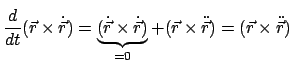
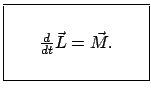
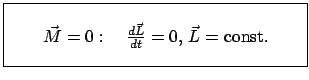
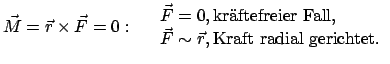
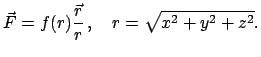
![]() darf nur vom Betrag
darf nur vom Betrag ![]() abhängen, nicht aber von den
einzelnen
Komponenten des Radiusvektors. Eine derartige Kraft besitzt immer ein Potential;
dieses ist radialsymmetrisch, nur eine Funktion von
abhängen, nicht aber von den
einzelnen
Komponenten des Radiusvektors. Eine derartige Kraft besitzt immer ein Potential;
dieses ist radialsymmetrisch, nur eine Funktion von ![]() :
:
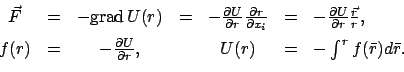
![]() beim Keplerproblem, die Vektoren
beim Keplerproblem, die Vektoren ![]() und
und ![]() für die Halbachsen
der Bahnellipse im
linearen Zentralkraftfeld, den Poincaréschen Vektor für die Lorentzkraft
im Feld eines einzelnen (hypothetischen) Magnetpoles (s. Ü5 zu Kap. 5).
für die Halbachsen
der Bahnellipse im
linearen Zentralkraftfeld, den Poincaréschen Vektor für die Lorentzkraft
im Feld eines einzelnen (hypothetischen) Magnetpoles (s. Ü5 zu Kap. 5).
![]() und die -geschwindigkeit
und die -geschwindigkeit
![]() . Leitet man die Lösung des
Problems zu diesen Anfangsdaten nach der Geschwindigkeit ab, erhält man:
. Leitet man die Lösung des
Problems zu diesen Anfangsdaten nach der Geschwindigkeit ab, erhält man:
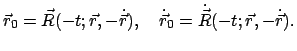
![]() ) ist dieser Phasenraum
zweidimensional, z.B.
) ist dieser Phasenraum
zweidimensional, z.B.
![]() , also eine Ebene. Bei 2 Freiheitsgraden ist der Phasenraum
vierdimensional, bei 3 sechsdimensional,..., allgemein 2f-dimensional. Da man einen
vier- oder noch höherdimensionalen Raum nicht darstellen kann, muß man sich leider meist
mit Projektionen dieses Raumes begenügen. Trotzdem geben diese Darstellungen oft sehr
nützliche Einsichten und werden häufig verwendet. Diese wird in den nachfolgenden
Kapiteln gezeigt werden.
, also eine Ebene. Bei 2 Freiheitsgraden ist der Phasenraum
vierdimensional, bei 3 sechsdimensional,..., allgemein 2f-dimensional. Da man einen
vier- oder noch höherdimensionalen Raum nicht darstellen kann, muß man sich leider meist
mit Projektionen dieses Raumes begenügen. Trotzdem geben diese Darstellungen oft sehr
nützliche Einsichten und werden häufig verwendet. Diese wird in den nachfolgenden
Kapiteln gezeigt werden.