Unterabschnitte
Die Bewegung eines Massenpunktes wird oft durch gewisse Bedingungen eingeschränkt
(E.: constrained motion),
die es ihm nicht gestatten, sich im ganzen Raum zu bewegen. Z.B.
kann die Bewegung auf eine vorgegebene Fläche eingeschränkt werden, oder es
kann ein bestimmter Bereich des Raumes unzugänglich sein. In manchen Fällen
lassen sich diese Nebenbedingungen (E.: constraints) analytisch durch Gleichungen oder
Ungleichungen darstellen. Hier werden nur solche betrachtet, die sich durch Gleichungen
der Art
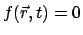 |
(61) |
darstellen lassen, d.h. daß sich der Körper auf einer Fläche bewegen muß;
oder durch die beiden Gleichungen
 |
(62) |
was bedeutet, daß sich der Körper unter dem Einfluß der Nebenbedingungen
auf der Schnittkurve der beiden Flächen bewegen muß. Hier wird immer angenommen,
daß diese Bewegung ohne Reibung abläuft. Die vorhergehenden
Fälle werden meist mit Hilfe von Zwangskräften behandelt. Wenn zwei
Nebenbedingungen die Beweglichkeit auf die Schnittkurve der beiden Flächen
einschränken, dann kann auch eine zweite Methode verwendet werden, bei der
die äußere Kraft auf diese Kurve projiziert wird.
Drei unabhängige
Nebenbedingungen würden eine Bewegung der Masse unmöglich machen.
Zuerst werden zwei Arten von Bewegungsgleichungen, die die Nebenbedingungen berücksichtigen,
abgeleitet. Diese werden dann für das sphärische, das mathematische und das
Zykloidenpendel spezialisiert und exakt gelöst.
Solche nichtlineare Bewegungsgleichungen,
die sich exakt lösen lassen, heißen integrabel. An diesen Beispielen werden wir
einige allgemeine Eigenschaften nichtlinerarer Bewegungen aufzeigen:
- Für verschiedene Energiewerte können ganz verschiedene Typen von Bewegungen auftreten,
S. Tabelle in §6.3.1 und Abb. 6.12.
- Bei Schwingungen hängt in den meisten Fällen die Schwingungsdauer von der Größe des
Maximalausschlags, damit von der Energie ab, s. Abb. 6.10 und Animation im Notebook
K6MathPend2.nb.
Ableitung der Bewegungsgleichungen. Zwangskräfte
Wenn sich ein Körper unter dem Einfluß einer Kraft bewegt, verläuft im allgemeinen
die Bewegung bei Bestehen von Nebenbedingungen anders als bei deren Abwesenheit.
Da jedem Einfluss auf die Bewegung eines Körpers in der Mechanik eine Kraft
zugeschrieben werden kann, wird auch in diesem Fall eine Kraft eingeführt, die für den geänderten Bewegungsablauf verantwortlich ist. Sie heisst
Zwangskraft (E.: reaction force);
man kann sich vorstellen, daß sie durch elastische Deformation der Führungen oder
Lager entsteht. Zum Unterschied heißt die vorgegebene Kraft, 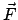 , so wie diese
in den früheren Kapiteln verwendet wurde, eingeprägte Kraft
(E.: impressed force).
, so wie diese
in den früheren Kapiteln verwendet wurde, eingeprägte Kraft
(E.: impressed force).
Man kann nach Definition der Zwangskraft die Bewegung so beschreiben, als ob
sich der Körper frei, aber unter dem Einfluß der Resultierenden der beiden
Kräfte bewegt:
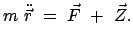 |
(63) |
Die Zwangskraft, 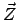 , hat zur Folge, daß sie das Verlassen der Fläche, also
Bewegungen senkrecht zur Fläche, verhindert. Man nimmt daher an, daß sie in der
Flächennormalen liegt und daher proportional zum Gradienten der Fläche ist:
, hat zur Folge, daß sie das Verlassen der Fläche, also
Bewegungen senkrecht zur Fläche, verhindert. Man nimmt daher an, daß sie in der
Flächennormalen liegt und daher proportional zum Gradienten der Fläche ist:
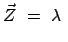 grad grad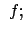 |
(64) |
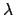 ist eine vorläufig nicht bestimmte Funktion der Zeit. Sie heisst
Lagrangescher Multiplikator (E.: Lagrangian multiplier).
Für zwei Nebenbedingungen folgt analog:
ist eine vorläufig nicht bestimmte Funktion der Zeit. Sie heisst
Lagrangescher Multiplikator (E.: Lagrangian multiplier).
Für zwei Nebenbedingungen folgt analog:
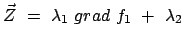 grad grad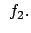 |
(65) |
Im Falle einer Nebenbedingung hat man also
das sind vier Gleichungen für die vier unbekannten Funktionen
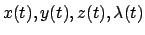 .
.
Bei zwei Nebenbedingungen hat man:
Das sind fünf Gleichungen für die fünf unbekannten Funktionen
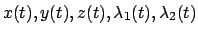 .
.
Im allgemeinen ist die Lösung dieser Gleichungen, die auch
Lagrangesche Gleichungen 1. Art genannt werden, schwierig, weil
es nur selten gelingt, eine Lösung der Differentialgleichungen an
die Nebenbedingungen anzupassen. Beim sphärischen Pendel ist es aber
bei kleinen Ausschlägen möglich, eine passende Näherungslösung
zu finden, s. §6.3.2.
Das zweite Verfahren ist anwendbar, wenn auf Grund der Nebenbedingungen
bereits eine Raumkurve festgelegt ist, auf der die Bewegung erfolgen muß.
Diese trifft zu, wenn
- zwei unabhängige Nebenbedingungen vorliegen, oder
- der Massenpunkt reibungsfrei auf einer Zylinderfläche gleitet und
die eingeprägte Kraft keine Komponente in Richtung der Erzeugenden hat.
Die Raumkurve sei durch eine Vektorfunktion gegeben, die von einem Parameter
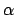 abhängt. Daraus berechnet man den Betrag der Geschwindigkeit und
dessen Zeitableitung gemäß der Kettenregel so wie in Kap.2:
abhängt. Daraus berechnet man den Betrag der Geschwindigkeit und
dessen Zeitableitung gemäß der Kettenregel so wie in Kap.2:
Der Apostroph bezeichnet hier die Ableitung nach 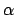 . Mittels
(2.6) bis (2.8) - bildet man aus
der vorhergehenden Gleichung die folgende; diese wird dann mit dem normierten Tangenvektor
multipliziert.
. Mittels
(2.6) bis (2.8) - bildet man aus
der vorhergehenden Gleichung die folgende; diese wird dann mit dem normierten Tangenvektor
multipliziert.
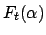 ist die Komponente der eingeprägten Kraft in Richtung der Kurventangente.
Mit der vorhergehenden Gleichung und Gl. (6.9) erhält man dann die Bewegungsgleichung:
ist die Komponente der eingeprägten Kraft in Richtung der Kurventangente.
Mit der vorhergehenden Gleichung und Gl. (6.9) erhält man dann die Bewegungsgleichung:
![$\displaystyle m \left( \left[ \sqrt{[\vec{r}{ '}(\alpha)]^2} \right]' \dot{...
... \sqrt{[\vec{r}{ '}(\alpha)]^2} \ddot{\alpha} \right) = F_t(\alpha) .$](img1085.gif) |
(610) |
Das Zykloidenpendel
Das Zykloidenpendel ist ein Pendel, bei dem sich eine Masse auf einer gemeinsamen
Zykloide (Radkurve) bewegt. Eine Zykloide entsteht, wenn ein Kreis auf einer Geraden
abrollt; dabei erzeugt ein bestimmter Punkt dieses Kreises die Kurve,
s. Abb. 6.1 und Animation im Notebook
K6ZykloidenPend.nb.
Diese Konstruktion (Abb. 6.1) liefert auch die Parameterdarstellung der Zykloide:
 |
(611) |
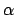 ist der Drehwinkel des Rades, durch dessen Rollen man sich die Kurve erzeugt
denken kann. Er wird unten zur Beschreibung der Bewegung verwendet werden.
ist der Drehwinkel des Rades, durch dessen Rollen man sich die Kurve erzeugt
denken kann. Er wird unten zur Beschreibung der Bewegung verwendet werden.
Abbildung 6.1:
Der Kreis (hier mit Radius 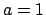 ) rollt auf der ihn oben berührenden Geraden ab.
Der Punkt des Kreises, der am Anfang auf der Geraden liegt, erzeugt die Zykloide.
Mathematica Notebook:
K6ZykloidenPend.nb.
) rollt auf der ihn oben berührenden Geraden ab.
Der Punkt des Kreises, der am Anfang auf der Geraden liegt, erzeugt die Zykloide.
Mathematica Notebook:
K6ZykloidenPend.nb.
|
|
Für die tangentielle Kraftkomponente liest man aus Abb. 6.2 ab:
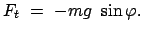 |
(612) |
Abbildung 6.2:
Die tangentielle Komponente der Schwerkraft.
|
|
Für die Ableitungen von x und y nach 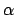 bzw. nach der Zeit
bzw. nach der Zeit  findet man:
findet man:
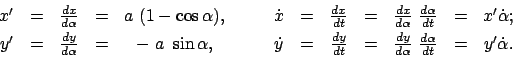 |
(613) |
Weiters gilt:
Damit berechnet man weiter:
Damit lautet die Bewegungsgleichung (6.10):
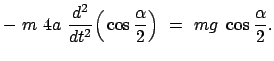 |
(614) |
Mit der Substitution
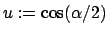 wird daraus die Schwingungsgleichung
deren zur Anfangsbedingung
wird daraus die Schwingungsgleichung
deren zur Anfangsbedingung
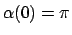 gehörige Lösung ist:
Der maximale Ausschlag des Pendels wird mit
gehörige Lösung ist:
Der maximale Ausschlag des Pendels wird mit 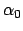 bezeichnet. Damit erhält man
aus obiger Lösung:
bezeichnet. Damit erhält man
aus obiger Lösung:
Damit ergibt sich für die Schwingungsdauer 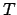 des Pendels:
des Pendels:
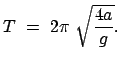 |
(615) |
Das Zykloidenpendel hat also die Eigenschaft, daß seine Schwingungsdauer streng
unabhängig vom Ausschlag ist. Diese Entdeckung stammt von Chr. Huygens (1673).
Im allgemeinen hängt die Schwingungsdauer eines Pendels (allgemeiner: die
einer nichtlinearen Schwingung) von der Größe des maximalen Ausschlags
ab. Im nächsten Paragraphen wird am Beispiel des mathematischen Pendels
gezeigt werden, daß die Schwingungsdauer des
gewöhnlichen mathematischen Pendels für Amplituden über 90^&cir#circ; sehr stark mit
steigendem Ausschlag zunimmt. (Animation im Notebook:
K6MathPend2.nb).
Insofern bildet das Zykloidenpendel eine wichtige Ausnahme
(s. Animation im Notebook:
K6ZykloidenPend.nb).
Das letzte Laufbild und Abb. 6.3 zeigen: Die Bewegung auf der
materiell nicht vorhandenen
Zykloide wird dadurch erzwungen, daß der Faden in seiner Bewegung durch die beiden
grauen Schablonen eingeschränkt wird. Letztere sind die Evolute (= Kurve
der Krümmungsmittelpunkte) der Bahnzykloide und stellen auch eine Zykloide
dar. (Dies ist ein wohlbekannter Satz der Differentialgeometrie.) Diese
Folge von Krümmungskreisen ist in Abb. 6.4 dargestellt;
sie werden als Animation im
Notebook: K6ZykloidenPend.nb)
vorgeführt.
Abbildung 6.3:
Zwei Schablonen in Gestalt zweier Teile einer Zykloide verkürzen den
Pendelfaden immer mehr je höher der Ausschläg. Dann läuft die Masse am
Endes des Fadens auf einer Zykloide. Notebook:
K6ZykloidenPend.nb.
|
|
Abbildung 6.4:
Jedem Punkt der Zykloide kann ein Krümmungskreis zugeordnet
werden. Deren Mittelpunkte liefern die Evolute. Notebook:
K6ZykloidenPend.nb.
|
|
Aufstellung der Bewegungsgleichungen. Unterscheidung der
verschiedenen Bewegungstypen mittels Drehimpuls- und Energiesatz
Unter einem sphärischen Pendel versteht man einen an einem masselos gedachten
Faden der Länge 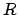 aufgehängten Massenpunkt; dadurch kann sich letzterer
nur auf der Oberfläche einer Kugel vom Radius
aufgehängten Massenpunkt; dadurch kann sich letzterer
nur auf der Oberfläche einer Kugel vom Radius 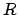 bewegen. Für den Fall, daß
der Massenpunkt bis in die obere Hälfte der Kugel gelangt, muß man sich den Faden
als eine masselose Stange denken.
bewegen. Für den Fall, daß
der Massenpunkt bis in die obere Hälfte der Kugel gelangt, muß man sich den Faden
als eine masselose Stange denken.
Legt man den Koordinatenursprung in den Kugelmittelpunkt, erhält man die
Gleichungen:
Mit
erhält man das folgende Differentialgleichungssystem:
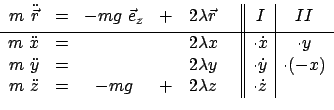 |
(617) |
Dieses wird wieder mittels Energie- und Drehimpulssatz reduziert. Zuerst wird
der Energiesatz abgeleitet. Multipliziert man die Gln. (6.17), wie in Kolonne I
angegeben, und addiert, findet man:
Differentiation der Nebenbedingung in Gl. (6.16) zeigt, daß der erste Term
auf der rechten Seite obiger Gleichung Null ist:
Damit ergibt sich aus der vorhergehenden Gleichung der Energiesatz:
![$\displaystyle \frac{d}{dt} \Big[ \frac{m}{2} \dot{\vec{r}}^{ 2} + m g z \Big] = 0, \qquad E = \dot{\vec{r}}^{ 2} + mgz = $](img1120.gif) const. const. |
(618) |
Die Erhaltung der z-Komponente des Drehimpulses beweist man, indem man die
ersten zwei Gln. (6.16) multipliziert wie in Kolonne II angegeben und addiert.
![$\displaystyle m (x\ddot{y} - \ddot{x} y) = \frac{d}{dt} [ m (x \dot{y} - \dot{x} y) ] = 0;
\qquad
L_z = m [x \dot{y} - \dot{x} y] = $](img1121.gif)
const.
Nun werden Kugelkoordinaten mit
 const. eingeführt. Damit ergeben sich folgende
Ausdrücke:
const. eingeführt. Damit ergeben sich folgende
Ausdrücke:
Setzt man diese Formeln in den obigen Ausdruck für den Drehimpuls ein, ergibt sich:
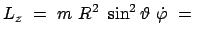 const. const. |
(619) |
Aus den obigen Formeln ergibt sich für das Quadrat der Geschwindigkeit
und damit für den Energiesatz:
![$\displaystyle E = \frac{m}{2} R^2 \Big[ \dot{\vartheta}^2 + \sin^2\vartheta \dot{\varphi}^2 \Big]
+ mg R \cos\vartheta = $](img1132.gif)
const.
Eliminiert man aus dieser Gleichung die Winkelgeschindigkeit
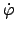 mittels des Drehimpulssatzes, (6.19), erhält man aus dem Energiesatz eine
Differentialgleichung 1. Ordnung für den Winkel
mittels des Drehimpulssatzes, (6.19), erhält man aus dem Energiesatz eine
Differentialgleichung 1. Ordnung für den Winkel  :
:
![$\displaystyle E = \frac{m}{2} R^2 \Big[ \dot{\vartheta}^2 + \frac{L_z^2}{m^2 R^4 \sin^2\vartheta} \Big]
+ mg R \cos\vartheta = $](img1134.gif)
const.
Diese Gleichung eignet sich besonders zur Bestimmung der verschiedenen Bewegungstypen. Es ist
bequemer mit dimensionslosen Verhältnissen zu arbeiten. So soll die Zeit (bzw. die Kreisfrequenz
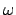 in Einheiten von
in Einheiten von 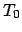 (bzw.
(bzw. 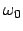 ), der Schwingungsdauer (bzw. Kreisfrequenz) für kleine
Schwingungen, Gl. (3.16), gemessen werden. Ebenso werden
statt der Gesamtenergie
), der Schwingungsdauer (bzw. Kreisfrequenz) für kleine
Schwingungen, Gl. (3.16), gemessen werden. Ebenso werden
statt der Gesamtenergie 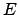 und der Komponente
des Drehimpulses
und der Komponente
des Drehimpulses 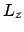 dimensionslose Verhältnisse
dimensionslose Verhältnisse 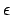 und
und 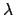 eingeführt:
eingeführt:
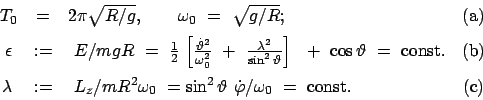 |
(620) |
Die Einführung dieser dimensionslosen Parameter reduziert die Zahl der zu untersuchenden
Größen beachtlich. Das System wird durch 2 Parameter 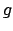 und
und 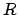 beschrieben;
diese werden zu dem einen wesentlichen, nämlich
beschrieben;
diese werden zu dem einen wesentlichen, nämlich 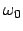 , zusammengefaßt.
Von den 6 Anfangswerten
, zusammengefaßt.
Von den 6 Anfangswerten 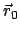 und
und
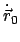 sind wegen der Nebenbedingung
sind wegen der Nebenbedingung
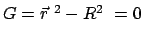 und der daraus folgenden Bedingung
und der daraus folgenden Bedingung
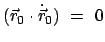 nur 4 unabhängig. An deren Stelle treten die zwei
wesentlichen Parameter
nur 4 unabhängig. An deren Stelle treten die zwei
wesentlichen Parameter
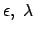 und zwei unwesentliche, z.B.
und zwei unwesentliche, z.B.
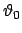 und
und 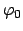 .
.
Aus den obigen Gleichungen (6.20) ergeben sich folgende Bewegungstypen:
Die Typen der Bewegung des sphärischen Pendels
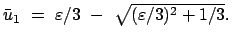
Fall a) entspricht den verschiedenen Bewegungsmöglichkeiten des mathematischen Pendels und
gibt nur Bewegungen des Massenpunktes auf einem (oder Teilen eines) vertikalen Kreises in der
Ebene
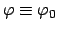 . In diesem Fall ist es zweckmässiger, statt des Polarwinkels
. In diesem Fall ist es zweckmässiger, statt des Polarwinkels
 den Winkel
den Winkel 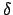 einzuführen, der von der negativen
einzuführen, der von der negativen 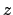 -Achse, d.i. von der
Ruhelage des Pendels, aus gezählt wird.
-Achse, d.i. von der
Ruhelage des Pendels, aus gezählt wird.
Abbildung 6.5:
Die Typen der Bewegung eines ebenen
Pendels. Notebook: K6MathPend1.nb.
|
|
Abbildung:
Die Bewegung des sphärischen Pendels bei
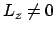 . Links: Die schwarzen
Breitenkreise markieren die zuläßige Zone. Rechts: Teil einer realen Bahn. Die
erste Periode wurde rot, die zweite blau strichliert gezeichnet.
Notebook: K6SpherPend1.nb.
. Links: Die schwarzen
Breitenkreise markieren die zuläßige Zone. Rechts: Teil einer realen Bahn. Die
erste Periode wurde rot, die zweite blau strichliert gezeichnet.
Notebook: K6SpherPend1.nb.
![\includegraphics[width=14cm]{K6sp1}](img1179.gif) |
Auflösen der Gl. (6.20 (b)) mit
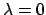 nach
nach
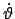 und Einführen von
und Einführen von 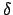 gibt:
gibt:
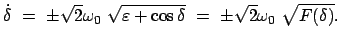 |
(621) |
Die Nullstellen des Radikanden 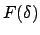 sind die Umkehrpunkte; in der
sind die Umkehrpunkte; in der
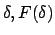 -Ebene sind dies die Schnittpunkte der Kurve
-Ebene sind dies die Schnittpunkte der Kurve
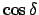 mit den
horizontalen Geraden
mit den
horizontalen Geraden
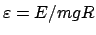 . Von diesen ausgehend sucht man den
Bereich, in dem
. Von diesen ausgehend sucht man den
Bereich, in dem
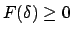 ist (s. Abb. 6.5) .
ist (s. Abb. 6.5) .
Im Falle b) (
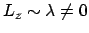 ) gibt es nur einen einzigen Bewegungstyp:
Der Massenpunkt bewegt sich in einer Kugelzone
) gibt es nur einen einzigen Bewegungstyp:
Der Massenpunkt bewegt sich in einer Kugelzone
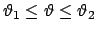 (s. Abb. 6.6).
Den Eintritt in die beiden Polkappenbereiche
(s. Abb. 6.6).
Den Eintritt in die beiden Polkappenbereiche
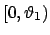 und
und
![$ (\vartheta_2, \pi ]$](img1190.gif) verhindert
die Fliehkraft. Die Energie
verhindert
die Fliehkraft. Die Energie 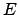 auf der linken Seite von Gl. (6.20 (b)) ist eine endliche
Konstante, der zweite Term auf der rechten Seite würde als einziger für
auf der linken Seite von Gl. (6.20 (b)) ist eine endliche
Konstante, der zweite Term auf der rechten Seite würde als einziger für
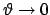 oder
oder
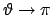 gegen Unendlich
streben. Die Vermeidung dieses Widerspruchs führt zur eben erwähnten Einschränkung.
An
gegen Unendlich
streben. Die Vermeidung dieses Widerspruchs führt zur eben erwähnten Einschränkung.
An
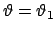 und
und
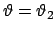 ist
ist
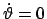 .
.
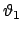 und
und
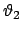 sind die Wurzeln der Gl. (6.20 (b))
für
sind die Wurzeln der Gl. (6.20 (b))
für
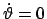 .
.
Dabei gibt es auch einen Spezialfall ebener Bewegung: Der
Massenpunkt läuft auf einem Breitenkreis:
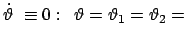 const. const.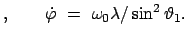 |
(622) |
Für die weitere qualitative Diskussion und für die analytische und numerische
Behandlung ist es zweckmässig, in Gl. (6.20 b)) folgende
Substitution der abhängigen Variablen vorzunehmen:
und den resultierenden Ausdruck nach 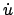 aufzulösen. Dadurch wird
die zu diskutierende Gleichung aus einer transzendenten in eine Polynomgleichung verwandelt.
aufzulösen. Dadurch wird
die zu diskutierende Gleichung aus einer transzendenten in eine Polynomgleichung verwandelt.
Der physikalische Bereich von 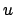 ist definiert durch die simultanen Bedingungen:
ist definiert durch die simultanen Bedingungen:
Er wird von zwei Nullstellen des Polynoms begrenzt. Diese werden willkürlich
als
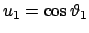 und
und
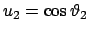 bezeichnet.
bezeichnet.
Zuerst wird nochmals der Fall des ebenen Pendels betrachtet:
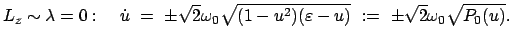 |
(625) |
Zur besseren Einsicht in das Verhalten der Funktion 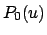 suchen wir deren Extrema auf:
suchen wir deren Extrema auf:
Aus den obigen Gleichungen und aus Abb. 6.7 ersieht man:
Maximum: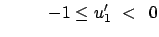 |
für |
 |
|
Minimum: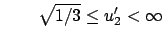 |
für |
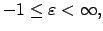 |
|
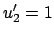 |
für |
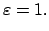 |
|
Abbildung 6.7:
Die Extrema 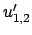 des Polynoms
des Polynoms
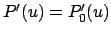 in Ihrer
Abhängigkeit vom dimensionlosen Energieparameter
in Ihrer
Abhängigkeit vom dimensionlosen Energieparameter
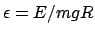 .
Notebook: K6SpherPlanePend.nb.
.
Notebook: K6SpherPlanePend.nb.
|
|
Abbildung:
Links: Die Typen des Polynoms 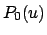 . Rechts unten: Das Bild für
. Rechts unten: Das Bild für 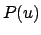 ergibt sich, indem man die
ergibt sich, indem man die 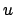 -Achse um
-Achse um
 nach oben verschiebt.
Rechts Mitte: Bei diesem Wert von
nach oben verschiebt.
Rechts Mitte: Bei diesem Wert von 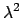 berührt die Kurve von
berührt die Kurve von 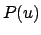 gerade
die
gerade
die 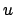 -Achse:
-Achse:
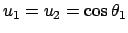 . Notebook:
K6SpherPlanePend.nb.
. Notebook:
K6SpherPlanePend.nb.
|
|
Aus Gl. (6.25) ersieht man die Wurzeln der Gleichung
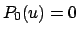 , aus den
Resultaten (6.26)
den qualitativen Verlauf von
, aus den
Resultaten (6.26)
den qualitativen Verlauf von 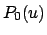 zwischen den Nullstellen. Es gibt entsprechend den
Typen a) der oben angegebenen Tabelle vier Typen von Diagrammen, s. Abb. 6.8.
zwischen den Nullstellen. Es gibt entsprechend den
Typen a) der oben angegebenen Tabelle vier Typen von Diagrammen, s. Abb. 6.8.
Man erhält das Diagramm für 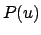 und damit die Wurzeln der Gleichung
und damit die Wurzeln der Gleichung 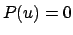 aus dem für
aus dem für 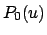 , indem man die
, indem man die 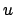 -Achse um
-Achse um
 nach oben verschiebt.
Man sieht aus Abb. 6.8 rechts unten:
nach oben verschiebt.
Man sieht aus Abb. 6.8 rechts unten:
Im speziellen Fall
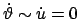 geht die
geht die 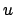 -Achse durch das Maximum
-Achse durch das Maximum
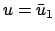 . Daher ist der Polarwinkel des entsprechenden Breitenkreises durch den Wert
der Energie (bzw. von
. Daher ist der Polarwinkel des entsprechenden Breitenkreises durch den Wert
der Energie (bzw. von
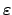 ) festgelegt (
) festgelegt (
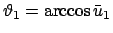 ).
).
Lineare Näherung für kleine Schwingungen
Für kleine Schwingungen bleibt der Massenpunkt in der Nähe der Ruhelage, der
Polarwinkel dann nahe bei 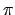 , der Winkel
, der Winkel 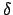 nahe bei 0. In der linearen
Näherung werden im Ausdruck der Kraft (des Potentials)
Glieder höherer als erster (zweiter) Ordnung in
nahe bei 0. In der linearen
Näherung werden im Ausdruck der Kraft (des Potentials)
Glieder höherer als erster (zweiter) Ordnung in 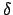 vernachlässigt:
vernachlässigt:
Der Fall ebener Bewegung (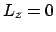 ) wurde in §12.2.2
bereits behandelt (dort
) wurde in §12.2.2
bereits behandelt (dort
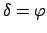 );
es ergaben sich harmonische Schwingungen der Kreisfrequenz
);
es ergaben sich harmonische Schwingungen der Kreisfrequenz 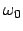 und der
Schwingungsdauer
und der
Schwingungsdauer 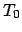 , Gl. (6.20a).
, Gl. (6.20a).
Bei sphärischer Bewegung (
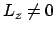 ) ist in der lineren Näherung
) ist in der lineren Näherung 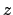 näherungsweise konstant, die zugehörige Beschleunigung Null;
der Lagrange Multiplikator
(nicht zu verwechseln mit dem dimensionslosen Drehimpulsparameter, Gl. (6.20c)
kann aus der dritten Gl. (6.17) berechnet
näherungsweise konstant, die zugehörige Beschleunigung Null;
der Lagrange Multiplikator
(nicht zu verwechseln mit dem dimensionslosen Drehimpulsparameter, Gl. (6.20c)
kann aus der dritten Gl. (6.17) berechnet
und in die ersten beiden Gleichungen (6.17) eingesetzt werden:
Die Lösungen sind harmonische Schwingungen der Schwingungsdauer 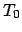 , Gl. (6.20a).
Die beiden Bewegungsgleichungen für die
, Gl. (6.20a).
Die beiden Bewegungsgleichungen für die 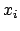 entsprechen denen des zweidimensionalen, isotropen
Harmonischen Oszillators. In §4.1.2 wurde bereits
gezeigt, daß dessen Bahnkurve im allgemeinen
eine zentrische Ellipse ist; die Länge und Lage der Halbachsen derselben hängen von den
Anfangsbdingungen ab. Für geeignete Anfangsbedingungen kann man diese Näherungslösung
schreiben als:
entsprechen denen des zweidimensionalen, isotropen
Harmonischen Oszillators. In §4.1.2 wurde bereits
gezeigt, daß dessen Bahnkurve im allgemeinen
eine zentrische Ellipse ist; die Länge und Lage der Halbachsen derselben hängen von den
Anfangsbdingungen ab. Für geeignete Anfangsbedingungen kann man diese Näherungslösung
schreiben als:
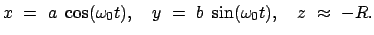 |
(627) |
Abbildung:
Projektion der Bahn eines sphärisches Pendel mit kleiner Schwingungsamplitude,
2^&cir#circ;
 6^&cir#circ;. Die Kreise sind die Projektionen der
entsprechenden Breitenkreise. Die Kreisstücke aussen sind Teile der Projektion
des Äquators
6^&cir#circ;. Die Kreise sind die Projektionen der
entsprechenden Breitenkreise. Die Kreisstücke aussen sind Teile der Projektion
des Äquators
 90^&cir#circ;. Notebook:
K6SpherPend1.nb.
90^&cir#circ;. Notebook:
K6SpherPend1.nb.
![\includegraphics[width = 15cm]{K6sp2}](img1244.gif) |
Strenge Lösung der Bewegungsgleichungen mittels elliptischer
Integrale
Die Bewegungsgleichungen des sphärischen und des mathematischen Pendels können
exakt mittels elliptischer Integrale und Funktionen gelöst werden. Dies
soll in diesem Paragraphen vorgeführt werden.
a1) Schwingung:
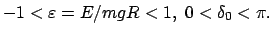
Um das Verständnis der bei der Lösung der nichtlinearen Differentialgleichung
auftretenden elliptischen Integrale und Funktionen zu erleichtern, werden im
folgenden der lineare und der nichtlineare Fall nebeneinander nach der gleichen
Methode behandelt. (
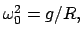 Gl. (6.20a)
Gl. (6.20a)
 Exakte Gleichung Exakte Gleichung
|
Der maximale Ausschlag
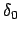 ergibt sich für
ergibt sich für
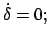 daraus wird die
Integrationskonstante bestimmt.
Der Zusammenhang mit
daraus wird die
Integrationskonstante bestimmt.
Der Zusammenhang mit
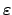 folgt aus Gl. (6.21).
folgt aus Gl. (6.21).
| |
|
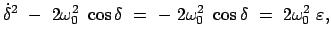 |
|
| |
|
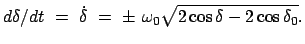 |
(628) |
|
In der letzten Zeile muß das Vorzeichen immer passend gewählt werden. Beim maximalen
Ausschlag des Pendels,
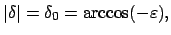 ist der Radikand
Null, das Pendel ändert seine Schwingungsrichtung, die Wurzel ihr Vorzeichen. Die obigen
Differentialgleichungen können durch Separation gelöst werden. Man erhält die
folgenden Integrale zur Anfangsbedingung
ist der Radikand
Null, das Pendel ändert seine Schwingungsrichtung, die Wurzel ihr Vorzeichen. Die obigen
Differentialgleichungen können durch Separation gelöst werden. Man erhält die
folgenden Integrale zur Anfangsbedingung
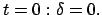
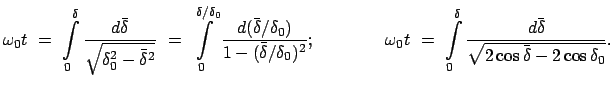 |
(629) |
Das linke Integral lässt sich elementar ausführen; das rechte muß durch
folgende Substitution auf die Normalform für elliptische Integrale gebracht werden.
Damit wird aus dem Integral in (6.29):
 Exakte Gleichung Exakte Gleichung
|
Beide Integrale geben die der momentanen Lage 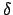 des Pendels entsprechende
Zeit als Funktionen zweier Veränderlicher. Links sind dies der maximale Ausschlag
des Pendels entsprechende
Zeit als Funktionen zweier Veränderlicher. Links sind dies der maximale Ausschlag
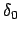 und der momentane Ausschlag
und der momentane Ausschlag 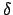 , rechts ist die Abhängigkeit von
diesen beiden Variablen etwas komplizierter.
, rechts ist die Abhängigkeit von
diesen beiden Variablen etwas komplizierter.
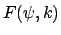 ist das unvollständige
elliptische Integral erster Gattung; es ist eine Funktion zweier unabhängiger
Variablen, des Moduls
ist das unvollständige
elliptische Integral erster Gattung; es ist eine Funktion zweier unabhängiger
Variablen, des Moduls 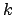 und der Amplitude
und der Amplitude 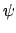 .
. 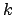 wird durch den Maximalausschlag
wird durch den Maximalausschlag
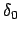 festgelegt (oder gleichwertig auch die durch die Gesamtenergie
festgelegt (oder gleichwertig auch die durch die Gesamtenergie 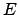 bzw.
bzw.
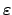 ).
Die Amplitude
).
Die Amplitude 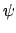 hängt vom momentanen Ausschlag
hängt vom momentanen Ausschlag 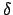 und vom maximalen
und vom maximalen 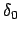 ab.
In der neueren Literatur (Abramowitz-Stegun) und auch in Mathematica wird statt des
Moduls
ab.
In der neueren Literatur (Abramowitz-Stegun) und auch in Mathematica wird statt des
Moduls 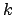 der Parameter
der Parameter
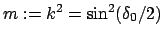 verwendet.
verwendet.
Die Periode der Schwingung ist 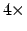 die Zeit für eine Bewegung von 0 bis
die Zeit für eine Bewegung von 0 bis
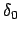 :
:
K(k) heisst vollständiges elliptisches Integral erster Gattung vom Modul 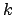 .
Damit schreibt man die Schwingungsdauer
.
Damit schreibt man die Schwingungsdauer 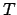 des Pendels für beliebige Ausschläge
des Pendels für beliebige Ausschläge
Abbildung 6.10:
Das vollständige elliptische Integral K und die relative
Schwingungsdauer 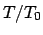 in Abhängigkeit vom halben Maximalausschlag
in Abhängigkeit vom halben Maximalausschlag
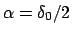 . Die Amplitudenabhängigkeit der Frequenz wird im
Notebook K6MathPend2.nb simuliert.
. Die Amplitudenabhängigkeit der Frequenz wird im
Notebook K6MathPend2.nb simuliert.
|
|
Man sieht, daß die Schwingungsdauer mit zunehmendem Maximalausschlag zunimmt, Abb. 6.10.
Für
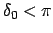 ist
ist 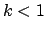 und T ist endlich.
Für
und T ist endlich.
Für
 ist
ist 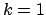 und T ist unendlich; das Pendel schwingt nach
oben, bis es verkehrt lotrecht steht. Dazu benötigt es aber unendlich lange
Zeit. Diese Tatsachen folgen aus den Eigenschaften des vollständigen
elliptischen Integrals erster Gattung, Abb. 6.10. Für dieses erhält man die obige
Reihenentwicklung, indem man den Integranden in eine (für
und T ist unendlich; das Pendel schwingt nach
oben, bis es verkehrt lotrecht steht. Dazu benötigt es aber unendlich lange
Zeit. Diese Tatsachen folgen aus den Eigenschaften des vollständigen
elliptischen Integrals erster Gattung, Abb. 6.10. Für dieses erhält man die obige
Reihenentwicklung, indem man den Integranden in eine (für 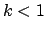 absolut und
gleichmässig konvergente) Binomialreihe entwickelt und dann gliedweise integriert:
absolut und
gleichmässig konvergente) Binomialreihe entwickelt und dann gliedweise integriert:
Für 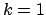 divergiert das Integral, die Schwingungsdauer wird unendlich.
divergiert das Integral, die Schwingungsdauer wird unendlich.
K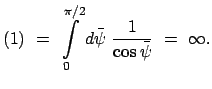 |
(633) |
Um den Ausschlag als Funktion der Zeit zu erhalten, muß man Gl. (6.29) nach der
Zeit  auflösen. Links ist dies einfach, rechts wird dies in zwei Schritten
ausgeführt. Zuerst drückt man die obere Grenze des Integrals als Funktion der
Zeit aus. Die dabei auftretende transzendente Funktion heißt die Jacobische
Amplitude
auflösen. Links ist dies einfach, rechts wird dies in zwei Schritten
ausgeführt. Zuerst drückt man die obere Grenze des Integrals als Funktion der
Zeit aus. Die dabei auftretende transzendente Funktion heißt die Jacobische
Amplitude
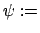 am
am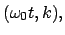 Abb. 6.11. Aus dem Integral (6.34),
das das elliptische Integral 1. Gattung definiert,
ersieht man, daß für kleine
Abb. 6.11. Aus dem Integral (6.34),
das das elliptische Integral 1. Gattung definiert,
ersieht man, daß für kleine 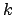 das Produkt
das Produkt
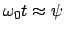 ist.
Für
ist.
Für 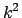 nahe bei 1, also
nahe bei 1, also 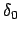 nahe bei 180^&cir#circ; überlagert sich noch eine
mit
nahe bei 180^&cir#circ; überlagert sich noch eine
mit 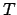 periodische wellige Kurve.
periodische wellige Kurve.
Im zweiten Schritt bildet man den Sinus und erhält die
Funktion
sn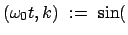 am
am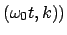 (sn = Sinus amplitudinis).
(sn = Sinus amplitudinis).
 Exakte Gleichung Exakte Gleichung
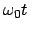 |
 |
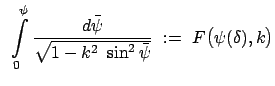 |
(634) |
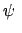 |
 |
 am am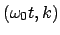 |
|
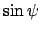 |
 |
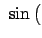 am am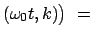 sn sn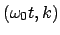 |
|
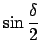 |
 |
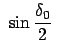 sn sn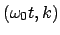 |
|
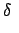 |
 |
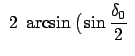 sn sn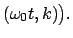 |
(635) |
|
Für 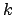 nicht zu nahe bei
nicht zu nahe bei 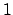 (nicht zu große Maximalausschläge
(nicht zu große Maximalausschläge 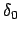 ) sieht
die Funktion sn wie ein gewöhnlicher Sinus aus, nur hat sie die Periode 4K
) sieht
die Funktion sn wie ein gewöhnlicher Sinus aus, nur hat sie die Periode 4K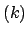 statt
statt 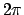 , Abbn. 6.11 und 6.12. Für
, Abbn. 6.11 und 6.12. Für 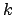 nahe bei
nahe bei 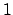 wird der sn eckiger.
(Durch die Wahl der Abszisse
wird der sn eckiger.
(Durch die Wahl der Abszisse 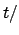 K werden die sn für verschiedene Werte von
K werden die sn für verschiedene Werte von 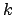 vergleichbar.)
vergleichbar.)
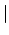 sn
sn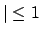 für reelle Argumente.
Deswegen oszilliert
für reelle Argumente.
Deswegen oszilliert 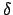 in Gl. (6.35) zwischen
in Gl. (6.35) zwischen
 und
und 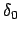 .
Wegen seiner Periodizität kann sn in eine Fourierreihe entwickelt werden.
.
Wegen seiner Periodizität kann sn in eine Fourierreihe entwickelt werden.
sn![$\displaystyle (u,k) = \frac{2 \pi}{k \mbox{\bf K}} \sum_{m=0}^\infty \fra...
...2}}{1 - q^{2m + 1}} \sin \Big[ (2 m + 1) \frac{\pi u}{2 \mbox{\bf K}} \Big]$](img1336.gif) |
(636) |
mit dem Nome:
Abbildung 6.11:
Links: Die Jacobische Amplitudenfunktion für verschiedene Werte des
Maximalausschlags 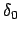 . Rechts: Die Jacobische elliptische Funktion sn
für verschiedene Werte des Maximalausschlags
. Rechts: Die Jacobische elliptische Funktion sn
für verschiedene Werte des Maximalausschlags 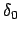 . Man beachte, daß
als Abszisse
. Man beachte, daß
als Abszisse 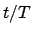 gewählt ist, damit die Kurven in ihrer Gestalt
vergleichbar sind. Notebook: K6MathPend2.nb.
gewählt ist, damit die Kurven in ihrer Gestalt
vergleichbar sind. Notebook: K6MathPend2.nb.
|
|
Abbildung:
Die Typen von Bewegungen eines ebenen Pendels (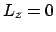 ) als Funktion der
Zeit. Als Abszisse dient
) als Funktion der
Zeit. Als Abszisse dient 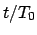 , um die unterschiedliche Länge der Perioden sichtbar
zu machen. Notebook: K6MathPend2.nb.
, um die unterschiedliche Länge der Perioden sichtbar
zu machen. Notebook: K6MathPend2.nb.
|
|
In Abb. 6.12 wird eine Schwingung mit mäßigen Maximalausschlag
(
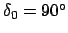 , lineare Näherung
noch brauchbar) mit einer Schwingung mit Maximalausschlag
, lineare Näherung
noch brauchbar) mit einer Schwingung mit Maximalausschlag
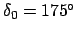 des gleichen Pendels
verglichen. Man sieht, wie letztere wegen der längeren Periode hinter der
ersteren zurückbleibt.
des gleichen Pendels
verglichen. Man sieht, wie letztere wegen der längeren Periode hinter der
ersteren zurückbleibt.
a2) Grenzfall:
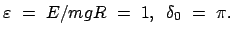
Das Pendel besitzt soviel Energie, daß es bis zur Vertikalen ausschwingen kann,
wenn auch mit unendlich langer Periode, Gln. (6.30) und (6.33).
Dieser Fall ist
mit elementaren Funktionen lösbar. Aus (6.28) folgt mit der Anfangsbedingung
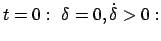
a3) Rotation :
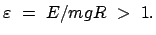
Das Pendel rotiert, daher nimmt 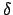 ständig zu (oder ab). Aus (6.21)
gewinnt man wieder eine Differentialgleichung, die durch Separation gelöst werden
kann. Der dabei auftretende Wurzelausdruck wird wieder durch eine Umformung und eine
Variablensubstitution auf die Standardform des elliptischen Integrals erster
Gattung gebracht:
ständig zu (oder ab). Aus (6.21)
gewinnt man wieder eine Differentialgleichung, die durch Separation gelöst werden
kann. Der dabei auftretende Wurzelausdruck wird wieder durch eine Umformung und eine
Variablensubstitution auf die Standardform des elliptischen Integrals erster
Gattung gebracht:
mit dem Modul 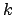 und der Amplitude
und der Amplitude 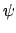 :
:
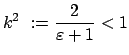
und
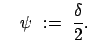
Mit der Anfangsbedingung
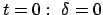 ,
,
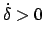 ergibt sich:
ergibt sich:
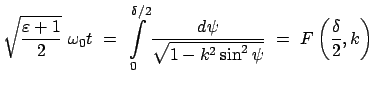 |
(639) |
Für die Hälfte einer Umlaufperiode 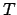 , innerhalb derer der Massenpunkt vom
tiefsten bis zum höchsten Punkt läuft, findet man:
, innerhalb derer der Massenpunkt vom
tiefsten bis zum höchsten Punkt läuft, findet man:
Um  als Funktion der Zeit zu bekommen, muß man Gl. (6.39) nach
als Funktion der Zeit zu bekommen, muß man Gl. (6.39) nach 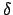 auflösen.
Die zu
auflösen.
Die zu 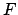 inverse Funktion ist die Jacobische Amplitudenfunktion am; diese besteht aus einem
linearen und einem mit
inverse Funktion ist die Jacobische Amplitudenfunktion am; diese besteht aus einem
linearen und einem mit
 periodischen Anteil
(Abb. 6.11, Links),
periodischen Anteil
(Abb. 6.11, Links),
mit dem Nome 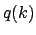 wie in (6.37). Damit bekommt man aus Gl. (6.39) eine Lösung,
die genau die in der Geschwindigkeit mit der Periode
wie in (6.37). Damit bekommt man aus Gl. (6.39) eine Lösung,
die genau die in der Geschwindigkeit mit der Periode 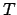 schwankende Rotation beschreibt:
schwankende Rotation beschreibt:
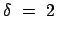 am am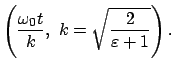 |
(642) |
Abb. 6.12 zeigt auch den zeitlichen Verlauf der ebenen Pendelbewegung im Grenzfall
(
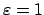 ,
,
 ) , für schnelle
) , für schnelle
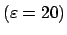 und langsame
und langsame
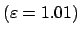 Rotation.
Rotation.
b) Räumliche Schwingung zwischen zwei Breitenkreisen
Abgesehen von den Spezialfällen
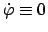 und
und
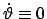 sind die drei Wurzeln
sind die drei Wurzeln 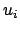 des Polynoms
des Polynoms 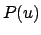 ,
Gl. (6.24), paarweise verschieden. Wegen
,
Gl. (6.24), paarweise verschieden. Wegen
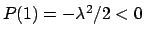 und
und
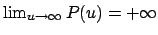 ist
ist 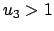 .
. 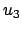 ist bekannt, sobald
ist bekannt, sobald 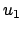 und
und 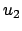 gefunden worden sind; wofür meist
ein numerisches Verfahren verwendet wird. Der physikalisch zulässige Bereich
von
gefunden worden sind; wofür meist
ein numerisches Verfahren verwendet wird. Der physikalisch zulässige Bereich
von
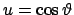 ist durch die folgenden Bedingungen
ist durch die folgenden Bedingungen
gegeben. In diesem wird Gl. (6.23) auf die Normalform des elliptischen
Integrals erster Gattung gebracht durch folgende Substitution:
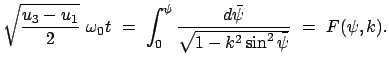 |
(643) |
Die Schwingungsdauer 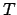 ist 4-mal die Zeit zwischen dem untersten und dem
obersten Punkt der Bahn:
ist 4-mal die Zeit zwischen dem untersten und dem
obersten Punkt der Bahn:
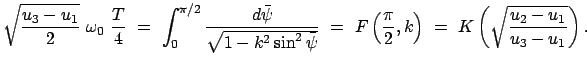 |
(644) |
Die Umkehrung des elliptischen Integrals in Gl. (6.43) geht analog
wie nach Gl. (6.34):
Die Änderung von  mit der Zeit
mit der Zeit  oder dem Hilfswinkel
oder dem Hilfswinkel 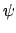 berechnet man aus
dem Drehimpulssatz (6.20c) zusammen mit der Lösung (6.45) oder
der obigen Substitution für
berechnet man aus
dem Drehimpulssatz (6.20c) zusammen mit der Lösung (6.45) oder
der obigen Substitution für 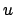 .
.
Das letzte Integral kann durch elliptische Integrale dritter Gattung dargestellt werden:
Da deren Berechnung manchmal schwierig ist, kann es einfacher, wenn auch
langsamer, sein
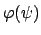 durch numerische
Integration des obigen Integrals (6.46) zu bestimmen. Dies wird erleichtert durch die
Symmetrieeigenschaften:
Einer vollen Periode
durch numerische
Integration des obigen Integrals (6.46) zu bestimmen. Dies wird erleichtert durch die
Symmetrieeigenschaften:
Einer vollen Periode 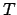 in der Zeit
in der Zeit  entspricht ein Zuwachs der Hilfsvariablen
entspricht ein Zuwachs der Hilfsvariablen 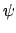 von 0 bis
von 0 bis 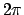 . Deswegen ist der Zuwachs von
. Deswegen ist der Zuwachs von  in einer Periode:
Die numerische Auswertung zeigt, daß
in einer Periode:
Die numerische Auswertung zeigt, daß
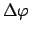 sehr klein ist für kleine
Schwingungen (vgl. Gl. (6.27) und Abb. 6.9).
Für Schwingungen endlicher
Amplitude ist
sehr klein ist für kleine
Schwingungen (vgl. Gl. (6.27) und Abb. 6.9).
Für Schwingungen endlicher
Amplitude ist
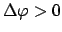 ; dies gibt einen Zuwachs des Azimuts eines
bestimmten Punktes (z.B.
; dies gibt einen Zuwachs des Azimuts eines
bestimmten Punktes (z.B.
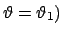 im Laufe einer Periode
(s. Abbn. 6.13 und 6.14). Daher ist im allgemeinen die Bewegung nicht
periodisch sondern mehrfach periodisch. Es gibt aber Ausnahmefälle streng periodischer
Bewegung, s. Animationen im Notebook:
K6SpherPend2.nb.
im Laufe einer Periode
(s. Abbn. 6.13 und 6.14). Daher ist im allgemeinen die Bewegung nicht
periodisch sondern mehrfach periodisch. Es gibt aber Ausnahmefälle streng periodischer
Bewegung, s. Animationen im Notebook:
K6SpherPend2.nb.
Abbildung 6.13:
Polarwinkel 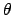 , Zeit
, Zeit  und Azimuth
und Azimuth 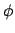 eines sphärisches Pendels
als Funktionen des Hilfswinkels
eines sphärisches Pendels
als Funktionen des Hilfswinkels 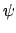 .
.
 Notebook: K6SpherPend1.nb.
Notebook: K6SpherPend1.nb.
|
|
Abbildung 6.14:
Projektion der räumlichen Schwingung eines sphärischen Pendels auf die
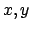 -Ebene.
-Ebene.
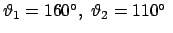 . Die erste Periode wurde
rot, die zweite blau strichliert gezeichnet. Die perspektivische Darstellung dieser
Bahnkurve wurde bereits in Abb. 6.6
gezeigt. Notebook: K6SpherPend1.nb.
. Die erste Periode wurde
rot, die zweite blau strichliert gezeichnet. Die perspektivische Darstellung dieser
Bahnkurve wurde bereits in Abb. 6.6
gezeigt. Notebook: K6SpherPend1.nb.
|
|
Christian Sommer
2003-01-27
![]() , so wie diese
in den früheren Kapiteln verwendet wurde, eingeprägte Kraft
(E.: impressed force).
, so wie diese
in den früheren Kapiteln verwendet wurde, eingeprägte Kraft
(E.: impressed force).
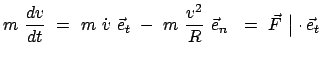
![\includegraphics[width=12cm]{K6zp1}](img1087.gif)
![]() bzw. nach der Zeit
bzw. nach der Zeit ![]() findet man:
findet man:
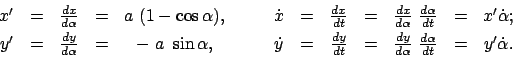
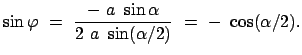
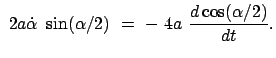
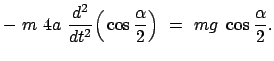
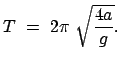
![\includegraphics[width=7cm]{K6zp3}](img1110.gif)
![\includegraphics[width=7cm]{K6zp4}](img1111.gif)
![]() aufgehängten Massenpunkt; dadurch kann sich letzterer
nur auf der Oberfläche einer Kugel vom Radius
aufgehängten Massenpunkt; dadurch kann sich letzterer
nur auf der Oberfläche einer Kugel vom Radius ![]() bewegen. Für den Fall, daß
der Massenpunkt bis in die obere Hälfte der Kugel gelangt, muß man sich den Faden
als eine masselose Stange denken.
bewegen. Für den Fall, daß
der Massenpunkt bis in die obere Hälfte der Kugel gelangt, muß man sich den Faden
als eine masselose Stange denken.
![$\displaystyle \frac{d}{dt} \Big[ \frac{m}{2} \dot{\vec{r}}^{ 2} + m g z \Big] = 0, \qquad E = \dot{\vec{r}}^{ 2} + mgz = $](img1120.gif) const.
const.![$\displaystyle m (x\ddot{y} - \ddot{x} y) = \frac{d}{dt} [ m (x \dot{y} - \dot{x} y) ] = 0;
\qquad
L_z = m [x \dot{y} - \dot{x} y] = $](img1121.gif) const.
const.
![$\displaystyle E = \frac{m}{2} R^2 \Big[ \dot{\vartheta}^2 + \frac{L_z^2}{m^2 R^4 \sin^2\vartheta} \Big]
+ mg R \cos\vartheta = $](img1134.gif) const.
const.
![]() . In diesem Fall ist es zweckmässiger, statt des Polarwinkels
. In diesem Fall ist es zweckmässiger, statt des Polarwinkels
![]() den Winkel
den Winkel ![]() einzuführen, der von der negativen
einzuführen, der von der negativen ![]() -Achse, d.i. von der
Ruhelage des Pendels, aus gezählt wird.
-Achse, d.i. von der
Ruhelage des Pendels, aus gezählt wird.
![\includegraphics[width=14cm]{K6sp1}](img1179.gif)
![]() nach
nach
![]() und Einführen von
und Einführen von ![]() gibt:
gibt:
![]() ) gibt es nur einen einzigen Bewegungstyp:
Der Massenpunkt bewegt sich in einer Kugelzone
) gibt es nur einen einzigen Bewegungstyp:
Der Massenpunkt bewegt sich in einer Kugelzone
![]() (s. Abb. 6.6).
Den Eintritt in die beiden Polkappenbereiche
(s. Abb. 6.6).
Den Eintritt in die beiden Polkappenbereiche
![]() und
und
![]() verhindert
die Fliehkraft. Die Energie
verhindert
die Fliehkraft. Die Energie ![]() auf der linken Seite von Gl. (6.20 (b)) ist eine endliche
Konstante, der zweite Term auf der rechten Seite würde als einziger für
auf der linken Seite von Gl. (6.20 (b)) ist eine endliche
Konstante, der zweite Term auf der rechten Seite würde als einziger für
![]() oder
oder
![]() gegen Unendlich
streben. Die Vermeidung dieses Widerspruchs führt zur eben erwähnten Einschränkung.
An
gegen Unendlich
streben. Die Vermeidung dieses Widerspruchs führt zur eben erwähnten Einschränkung.
An
![]() und
und
![]() ist
ist
![]() .
.
![]() und
und
![]() sind die Wurzeln der Gl. (6.20 (b))
für
sind die Wurzeln der Gl. (6.20 (b))
für
![]() .
.
![]() ist definiert durch die simultanen Bedingungen:
ist definiert durch die simultanen Bedingungen:
![\includegraphics[height = 5cm]{K6msp1}](img1222.gif)
![\includegraphics[width=12cm]{K6msp2}](img1224.gif)
![]() und damit die Wurzeln der Gleichung
und damit die Wurzeln der Gleichung ![]() aus dem für
aus dem für ![]() , indem man die
, indem man die ![]() -Achse um
-Achse um
![]() nach oben verschiebt.
Man sieht aus Abb. 6.8 rechts unten:
nach oben verschiebt.
Man sieht aus Abb. 6.8 rechts unten:
![]() geht die
geht die ![]() -Achse durch das Maximum
-Achse durch das Maximum
![]() . Daher ist der Polarwinkel des entsprechenden Breitenkreises durch den Wert
der Energie (bzw. von
. Daher ist der Polarwinkel des entsprechenden Breitenkreises durch den Wert
der Energie (bzw. von
![]() ) festgelegt (
) festgelegt (
![]() ).
).
![]() , der Winkel
, der Winkel ![]() nahe bei 0. In der linearen
Näherung werden im Ausdruck der Kraft (des Potentials)
Glieder höherer als erster (zweiter) Ordnung in
nahe bei 0. In der linearen
Näherung werden im Ausdruck der Kraft (des Potentials)
Glieder höherer als erster (zweiter) Ordnung in ![]() vernachlässigt:
vernachlässigt:
![]() ) ist in der lineren Näherung
) ist in der lineren Näherung ![]() näherungsweise konstant, die zugehörige Beschleunigung Null;
der Lagrange Multiplikator
(nicht zu verwechseln mit dem dimensionslosen Drehimpulsparameter, Gl. (6.20c)
kann aus der dritten Gl. (6.17) berechnet
näherungsweise konstant, die zugehörige Beschleunigung Null;
der Lagrange Multiplikator
(nicht zu verwechseln mit dem dimensionslosen Drehimpulsparameter, Gl. (6.20c)
kann aus der dritten Gl. (6.17) berechnet
![\includegraphics[width = 15cm]{K6sp2}](img1244.gif)
![]()
![]() Gl. (6.20a)
Gl. (6.20a)
![]() ergibt sich für
ergibt sich für
![]() daraus wird die
Integrationskonstante bestimmt.
Der Zusammenhang mit
daraus wird die
Integrationskonstante bestimmt.
Der Zusammenhang mit
![]() folgt aus Gl. (6.21).
folgt aus Gl. (6.21).
![]() ist der Radikand
Null, das Pendel ändert seine Schwingungsrichtung, die Wurzel ihr Vorzeichen. Die obigen
Differentialgleichungen können durch Separation gelöst werden. Man erhält die
folgenden Integrale zur Anfangsbedingung
ist der Radikand
Null, das Pendel ändert seine Schwingungsrichtung, die Wurzel ihr Vorzeichen. Die obigen
Differentialgleichungen können durch Separation gelöst werden. Man erhält die
folgenden Integrale zur Anfangsbedingung
![]()
![]() des Pendels entsprechende
Zeit als Funktionen zweier Veränderlicher. Links sind dies der maximale Ausschlag
des Pendels entsprechende
Zeit als Funktionen zweier Veränderlicher. Links sind dies der maximale Ausschlag
![]() und der momentane Ausschlag
und der momentane Ausschlag ![]() , rechts ist die Abhängigkeit von
diesen beiden Variablen etwas komplizierter.
, rechts ist die Abhängigkeit von
diesen beiden Variablen etwas komplizierter.
![]() ist das unvollständige
elliptische Integral erster Gattung; es ist eine Funktion zweier unabhängiger
Variablen, des Moduls
ist das unvollständige
elliptische Integral erster Gattung; es ist eine Funktion zweier unabhängiger
Variablen, des Moduls ![]() und der Amplitude
und der Amplitude ![]() .
. ![]() wird durch den Maximalausschlag
wird durch den Maximalausschlag
![]() festgelegt (oder gleichwertig auch die durch die Gesamtenergie
festgelegt (oder gleichwertig auch die durch die Gesamtenergie ![]() bzw.
bzw.
![]() ).
Die Amplitude
).
Die Amplitude ![]() hängt vom momentanen Ausschlag
hängt vom momentanen Ausschlag ![]() und vom maximalen
und vom maximalen ![]() ab.
In der neueren Literatur (Abramowitz-Stegun) und auch in Mathematica wird statt des
Moduls
ab.
In der neueren Literatur (Abramowitz-Stegun) und auch in Mathematica wird statt des
Moduls ![]() der Parameter
der Parameter
![]() verwendet.
verwendet.
![]() die Zeit für eine Bewegung von 0 bis
die Zeit für eine Bewegung von 0 bis
![]() :
: ![]() .
Damit schreibt man die Schwingungsdauer
.
Damit schreibt man die Schwingungsdauer ![]() des Pendels für beliebige Ausschläge
des Pendels für beliebige Ausschläge
![\includegraphics[width=10cm]{K6mp3}](img1302.gif)
![$\displaystyle \int\limits_0^{\pi/2} d\bar{\psi} \
[1 - k^2 \sin^2\bar{\psi}]^{-1/2}$](img1308.gif)
![$\displaystyle \int\limits_0^{\pi/2} d\bar{\psi} \Big[ 1 + \frac{1}{2} \...
...si}
+ \frac{1 \cdot 3}{2 \cdot 4} k^4 \sin^4 \bar{\psi} + \dots \Big] .$](img1309.gif)
![]() auflösen. Links ist dies einfach, rechts wird dies in zwei Schritten
ausgeführt. Zuerst drückt man die obere Grenze des Integrals als Funktion der
Zeit aus. Die dabei auftretende transzendente Funktion heißt die Jacobische
Amplitude
auflösen. Links ist dies einfach, rechts wird dies in zwei Schritten
ausgeführt. Zuerst drückt man die obere Grenze des Integrals als Funktion der
Zeit aus. Die dabei auftretende transzendente Funktion heißt die Jacobische
Amplitude
![]() am
am![]() Abb. 6.11. Aus dem Integral (6.34),
das das elliptische Integral 1. Gattung definiert,
ersieht man, daß für kleine
Abb. 6.11. Aus dem Integral (6.34),
das das elliptische Integral 1. Gattung definiert,
ersieht man, daß für kleine ![]() das Produkt
das Produkt
![]() ist.
Für
ist.
Für ![]() nahe bei 1, also
nahe bei 1, also ![]() nahe bei 180^&cir#circ; überlagert sich noch eine
mit
nahe bei 180^&cir#circ; überlagert sich noch eine
mit ![]() periodische wellige Kurve.
periodische wellige Kurve.
![]() am
am![]() (sn = Sinus amplitudinis).
(sn = Sinus amplitudinis).
![]() nicht zu nahe bei
nicht zu nahe bei ![]() (nicht zu große Maximalausschläge
(nicht zu große Maximalausschläge ![]() ) sieht
die Funktion sn wie ein gewöhnlicher Sinus aus, nur hat sie die Periode 4K
) sieht
die Funktion sn wie ein gewöhnlicher Sinus aus, nur hat sie die Periode 4K![]() statt
statt ![]() , Abbn. 6.11 und 6.12. Für
, Abbn. 6.11 und 6.12. Für ![]() nahe bei
nahe bei ![]() wird der sn eckiger.
(Durch die Wahl der Abszisse
wird der sn eckiger.
(Durch die Wahl der Abszisse ![]() K werden die sn für verschiedene Werte von
K werden die sn für verschiedene Werte von ![]() vergleichbar.)
vergleichbar.)
![]() sn
sn![]() für reelle Argumente.
Deswegen oszilliert
für reelle Argumente.
Deswegen oszilliert ![]() in Gl. (6.35) zwischen
in Gl. (6.35) zwischen
![]() und
und ![]() .
Wegen seiner Periodizität kann sn in eine Fourierreihe entwickelt werden.
.
Wegen seiner Periodizität kann sn in eine Fourierreihe entwickelt werden.
![$\displaystyle (u,k) = \frac{2 \pi}{k \mbox{\bf K}} \sum_{m=0}^\infty \fra...
...2}}{1 - q^{2m + 1}} \sin \Big[ (2 m + 1) \frac{\pi u}{2 \mbox{\bf K}} \Big]$](img1336.gif)
![\includegraphics[width=15cm]{K6mp4}](img1340.gif)
![\includegraphics[width=14cm]{K6mp5}](img1341.gif)
![]() , lineare Näherung
noch brauchbar) mit einer Schwingung mit Maximalausschlag
, lineare Näherung
noch brauchbar) mit einer Schwingung mit Maximalausschlag
![]() des gleichen Pendels
verglichen. Man sieht, wie letztere wegen der längeren Periode hinter der
ersteren zurückbleibt.
des gleichen Pendels
verglichen. Man sieht, wie letztere wegen der längeren Periode hinter der
ersteren zurückbleibt.
![]()
![]()
![]()
![]() ständig zu (oder ab). Aus (6.21)
gewinnt man wieder eine Differentialgleichung, die durch Separation gelöst werden
kann. Der dabei auftretende Wurzelausdruck wird wieder durch eine Umformung und eine
Variablensubstitution auf die Standardform des elliptischen Integrals erster
Gattung gebracht:
ständig zu (oder ab). Aus (6.21)
gewinnt man wieder eine Differentialgleichung, die durch Separation gelöst werden
kann. Der dabei auftretende Wurzelausdruck wird wieder durch eine Umformung und eine
Variablensubstitution auf die Standardform des elliptischen Integrals erster
Gattung gebracht:
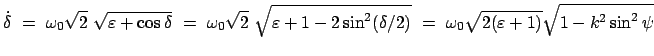
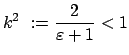 und
und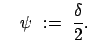
![]() als Funktion der Zeit zu bekommen, muß man Gl. (6.39) nach
als Funktion der Zeit zu bekommen, muß man Gl. (6.39) nach ![]() auflösen.
Die zu
auflösen.
Die zu ![]() inverse Funktion ist die Jacobische Amplitudenfunktion am; diese besteht aus einem
linearen und einem mit
inverse Funktion ist die Jacobische Amplitudenfunktion am; diese besteht aus einem
linearen und einem mit
![]() periodischen Anteil
(Abb. 6.11, Links),
periodischen Anteil
(Abb. 6.11, Links),
![]() ,
,
![]() ) , für schnelle
) , für schnelle
![]() und langsame
und langsame
![]() Rotation.
Rotation.
![]() und
und
![]() sind die drei Wurzeln
sind die drei Wurzeln ![]() des Polynoms
des Polynoms ![]() ,
Gl. (6.24), paarweise verschieden. Wegen
,
Gl. (6.24), paarweise verschieden. Wegen
![]() und
und
![]() ist
ist ![]() .
. ![]() ist bekannt, sobald
ist bekannt, sobald ![]() und
und ![]() gefunden worden sind; wofür meist
ein numerisches Verfahren verwendet wird. Der physikalisch zulässige Bereich
von
gefunden worden sind; wofür meist
ein numerisches Verfahren verwendet wird. Der physikalisch zulässige Bereich
von
![]() ist durch die folgenden Bedingungen
ist durch die folgenden Bedingungen
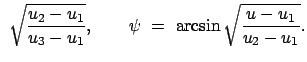
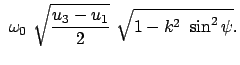
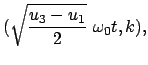
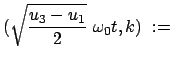 sn
sn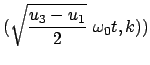
![$\displaystyle \varphi(\psi) = \frac{\lambda \sqrt{2}}{\sqrt{u_3 - u_1}} \
...
...2,k) + \
\frac{1}{1 + u_1} \Pi(\psi,\alpha_2^2,k) \right] . \hspace{3.6cm}$](img1410.gif)
![\includegraphics[width = 12.5cm]{K6sp3}](img1420.gif)
![\includegraphics[width=8cm]{K6sp4}](img1422.gif)