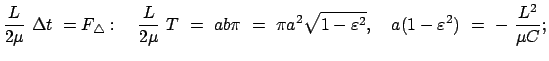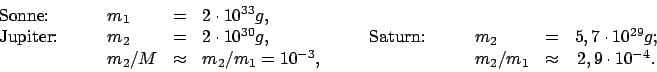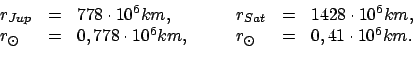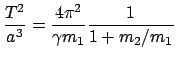Unterabschnitte
Systeme von Massenpunkten
Bisher ist nur die Bewegung eines einzelnen Massenpunktes im Felde äußerer
Kräfte untersucht worden. Nun soll der Fall von mehreren Massenpunkten
untersucht werden. Zuerst werden die Bewegungsgleichungen aufgestellt und
die grundlegenden Eigenschaften der Lösungen diskutiert.
Das System besteht aus 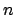 Massenpunkten. Der
Massenpunkten. Der 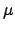 -te Massenpunkt hat die
Masse
-te Massenpunkt hat die
Masse 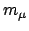 . Seine augenblickliche Lage wird durch den Vektor
. Seine augenblickliche Lage wird durch den Vektor
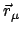 angegeben,
s. Abb. 7.1(a). Die Bewegung des
angegeben,
s. Abb. 7.1(a). Die Bewegung des 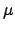 -ten
Massenpunktes wird durch die Newtonsche
Bewegungsgleichung beschrieben:
-ten
Massenpunktes wird durch die Newtonsche
Bewegungsgleichung beschrieben:
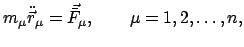 |
(71) |
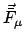 ist die Resultierende aller am
ist die Resultierende aller am 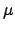 -ten Massenpunkt
angreifenden Kräfte. Die obigen
-ten Massenpunkt
angreifenden Kräfte. Die obigen 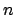 Vektorgleichungen
(7.1) bilden ein System
von
Vektorgleichungen
(7.1) bilden ein System
von 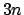 gewöhnlichen Differentialgleichungen 2. Ordnung.
gewöhnlichen Differentialgleichungen 2. Ordnung.
Abbildung 7.1:
a) Lage mehrerer Massenpunkte; b) Reaktionsprinzip.
|
[]
![\includegraphics[scale=0.8]{k7_lage_massenpkte}](img1428.gif) []
[]
![\includegraphics[scale=0.8]{k7_reaktionsprinzip}](img1429.gif) |
Die Kräfte werden in 2 Gruppen geteilt:
- Äußere Kräfte:
Sie hängen nur von den Koordinaten des
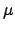 -ten Teilchens und eventuell von
dessen Geschwindigkeit und von der Zeit ab. Äußere Parameter sind z.B. elektrische
und magnetische Feldstärke oder andere physikalische Größen, die die
Kraft charakterisieren und unabhängig von
-ten Teilchens und eventuell von
dessen Geschwindigkeit und von der Zeit ab. Äußere Parameter sind z.B. elektrische
und magnetische Feldstärke oder andere physikalische Größen, die die
Kraft charakterisieren und unabhängig von
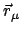 und
und
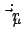 sind.
sind.
- Innere Kräfte: (Wechselwirkung der Massenpunkte untereinander)
Für diese werden nur Zweikörperkräfte in Betracht gezogen.
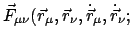
Parameter der Massenpunkte
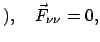
ist die Kraft des 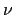 -ten Massenpunktes auf den
-ten Massenpunktes auf den 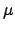 -ten Massenpunkt.
Parameter der Massenpunkte sind z.B. ihre Masse, ihre Ladung, ihre elektrischen und
magnetischen Momente, usw. Die Wechselwirkung eines Massenpunktes mit sich selbst,
-ten Massenpunkt.
Parameter der Massenpunkte sind z.B. ihre Masse, ihre Ladung, ihre elektrischen und
magnetischen Momente, usw. Die Wechselwirkung eines Massenpunktes mit sich selbst,
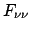 , wird Null gesetzt.
, wird Null gesetzt.
In der Natur entstehen die Kräfte durch Wechselwirkung der Teilchen, im
Prinzip gibt es also nur innere Kräfte. Aber oft kann ein System in zwei
Teile geteilt werden, sodaß die Wirkung des ersten Teiles auf den zweiten
vernachlässigt werden kann. Dann kann man die Kraft des zweiten Teiles auf
den ersten als äußere Kraft behandeln. Die Wechselwirkung der Bestandteile
des ersten Teiles untereinander gibt die inneren Kräfte.
Die inneren Kräfte sollen zwei Voraussetzungen erfüllen:
- Das Reaktionsprinzip (3. Newtonsches Axiom, actio = reactio)
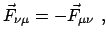 |
(72) |
ist ein allgemeines Grundgesetz der Mechanik (s. Abb. 7.1 b)).
- Die inneren Kräfte sind Zentralkräfte, sie hängen nur vom relativen
Abstand
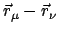 der beiden Massenpunkte ab und wirken
nur in der Verbindungslinie
der beiden Massenpunkte ab und wirken
nur in der Verbindungslinie
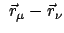
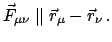 |
(73) |
Dies ist grundsätzlich naheliegend, weil für die beiden Massenpunkte ist im
freien Raum
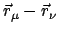 die einzige ausgezeichnete Richtung.
Die meisten Kräfte in der Natur erfüllen diese Bedingung.
die einzige ausgezeichnete Richtung.
Die meisten Kräfte in der Natur erfüllen diese Bedingung.
Man kann zwei Arten von Systemen unterscheiden:
- Freie Systeme: Die Massenpunkte sind bei der Bewegung unbehindert
und folgen nur den einwirkenden eingeprägten Kräften.
- Gebundene Systeme: Für die Koordinaten und/oder Geschwindigkeiten der
Massenpunkte liegen einschränkende Bedingungen vor, z.B. der Abstand der
Massenpunkte muß immer konstant bleiben (starrer Körper), oder die
Massenpunkte müssen sich auf vorgeschriebenen Kurven oder Flächen bewegen.
Diese Nebenbedingungen müssen dann durch die Einführung von Zwangskräften
berücksichtigt werden.
Hier werden nur freie Systeme betrachtet. Die Erhaltungssätze werden aus den
Bewegungsgleichungen abgeleitet:
 |
(74) |
Die Gesamtgrößen (Gesamtimpuls, -masse, -drehimpuls, usw.) sind definiert
als die Summen der entsprechenden Einzelgrößen. Für griechische Indices kein
Summationsübereinkommen.
 ist immer
ist immer
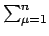 , ebenso
für
, ebenso
für 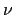 . Der Gesamtimpuls ist
. Der Gesamtimpuls ist
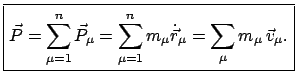 |
(75) |
Durch Summation der Bewegungsgleichung (7.4) ergibt sich
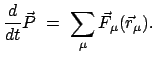 |
(76) |
In der oberen Zeile ist die Doppelsumme auf der rechten Seite Null wegen des
Reaktionsprinzipes, Gl. (7.3). Nun werden Schwerpunkt
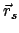 und
Gesamtmasse
und
Gesamtmasse 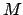 eingeführt.
eingeführt.
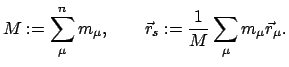 |
(77) |
Aus Gl. (7.5) und (7.7) folgt dann
![$\displaystyle \begin{tabular}{\vert rcl\vert} \hline && [-.8mm] $ \vec P $ \...
... = \sum_{\mu} \vec F_{\mu}(\vec r_{\mu}). $ [4mm] \hline \end{tabular}$](img1449.gif) |
(78) |
Die zeitliche Änderung des Gesamtimpulses wird nur von den äußeren
Kräften verursacht, die inneren können dazu nichts beitragen. Der Schwerpunkt
bewegt sich so, als ob die gesamte Masse des Systems in ihm vereinigt wäre
und alle äußeren Kräfte nur an diesem Punkt angriffen. Dies ist eine
Folge des Reaktionsprinzipes.
Ist die Resultierende der äußeren Kräfte Null (meist wird dies nur der Fall
sein, wenn alle
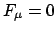 sind), dann gilt der Erhaltungssatz des
Impulses und des Anfangsschwerpunktes:
sind), dann gilt der Erhaltungssatz des
Impulses und des Anfangsschwerpunktes:
Bei Abwesenheit äußerer Kräfte
ist der Gesamtimpuls konstant; der Schwerpunkt bewegt sich mit gleichförmiger
Geschwindigkeit.
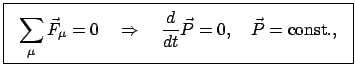 |
(79) |
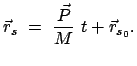 |
(710) |
Gesamtdrehimpuls
Die Bewegungsgleichung (7.4) wird von links mit
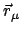 äußerlich
multipliziert und das Produkt über
äußerlich
multipliziert und das Produkt über  summiert. Dies gibt
summiert. Dies gibt
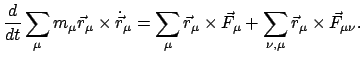 |
(711) |
Die zweite Summe auf der rechten Seite wird in zwei aufgespalten, in der so
erhaltenen zweiten Summe werden die Summationsindices umbenannt.
Nach diesen Umformungen sieht man, daß der Beitrag der inneren Kräfte
verschwindet, wenn diese Zentralkräfte, Gl. (7.3), sind.
Mittels der Definitionen des Gesamtdrehimpulses und -momentes
der äußeren Kräfte läßt sich Gl. (7.11) schreiben als
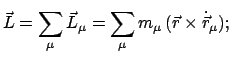 |
(712) |
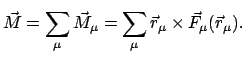 |
(713) |
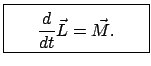 |
(714) |
Die zeitliche Änderung des gesamten Drehimpulses eines Systems ist gleich
dem resultierenden Drehmoment der äußeren Kräfte. Auch hier spielen die
inneren Kräfte keine Rolle, solange sie Zentralkräfte sind.
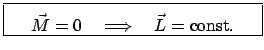 |
(715) |
Erhaltung des Gesamtdrehimpulses ist gewährleistet, wenn das resultierende
Moment der äußeren Kräfte Null und die inneren Kräfte Zentralkräfte sind.
Im allgemeinen ist der Drehimpuls vom Bezugspunkt abhängig.
Eine ungünstige Wahl des Bezugspunktes kann daher eine zeitliche Veränderung
des Drehimpulses, also eine Verletzung der Drehimpulserhaltung vortäuschen.
Geht man vom Bezugspunkt 0 zum neuen 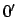 im Abstand
im Abstand
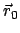 (Abb. 7.2(a))
über, ergibt einfache Ausrechnung:
(Abb. 7.2(a))
über, ergibt einfache Ausrechnung:
Abbildung:
a) Wechsel des Bezugspunktes; b)
Schwerpunktsbewegung ohne äußere Kräfte.
|
[]
![\includegraphics[scale=0.63]{k7_wechsel_bezugsys}](img1463.gif) []
[]
![\includegraphics[scale=0.63]{k7_schwerpuntsbew}](img1464.gif) |
Aus der vorhergehenden Gleichung ersieht man, daß
 ,
also der Wert des Drehimpulses unverändert bleibt, wenn
,
also der Wert des Drehimpulses unverändert bleibt, wenn
- der Bezugspunkt
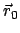 und der Schwerpunkt
und der Schwerpunkt
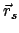 in Ruhe sind:
in Ruhe sind:
oder
- der Schwerpunkt der Bezugspunkt ist (dieser muß dann nicht in Ruhe sein
(vgl. Abb. 7.2(b)):
Die Bewegungsgleichung (7.4) wird mit
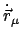 innerlich multipliziert,
das Produkt über
innerlich multipliziert,
das Produkt über 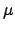 summiert. Der Ausdruck auf der linken Seite ist die gesamte kinetische
Energie
summiert. Der Ausdruck auf der linken Seite ist die gesamte kinetische
Energie 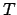 :
:
Wird die vorletzte Gleichung über die Zeit integriert, ergibt sich:
Die Änderung der kinetischen Energie ist gleich der von den äußeren
und inneren Kräften geleisteten Arbeit. Hier fällt der Beitrag der inneren
Kräfte nicht heraus wie bei den Sätzen für den Gesamtimpuls, Gl. (7.8), und für den
Gesamtdrehimpuls, Gln. (7.13), (7.14).
Wir nehmen zusätzlich an, daß die äußeren und inneren Kräfte Potentiale besitzen:
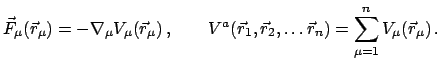 |
(718) |
Der Nablaoperator
 wirkt nur auf den Ortsvektor
wirkt nur auf den Ortsvektor
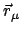 .
.
Für die inneren Kräfte können wir wegen der Voraussetzung, daß sie Zentralkräfte sind,
Gl. (7.3), ansetzen:
Das Reaktionsprinzip, Gl. (7.2), verlangt nun
Setzen wir nun
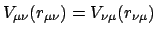 |
(721) |
(z.B. ist das Potential zwischen zwei Ladungen
von dieser Form), so ist die obige Bedingung, Gl. (7.21), erfüllt.
Wegen (7.19) und (7.21) bekommen wir:
In der Summe für die von den inneren Kräften geleistete Arbeit werden
jeweils die obigen beiden Ausdrücke zusammengefaßt:
Gl. (7.17) kann damit in folgender Weise umgeschrieben werden
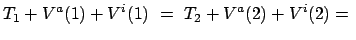
const.
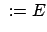
Dies gibt den Satz von der Erhaltung der Energie
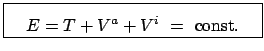 |
(722) |
mit
Die kinetische Energie kann noch umgeschrieben werden, indem man den Schwerpunkt
als Bezugspunkt einführt:
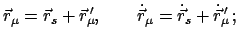 |
(723) |
![\begin{displaymath}\begin{array}{ccccccccc} T & = & \sum_{\mu} \frac{m_{\mu}}{2}...
...}^{2} && [1em] &&& = & T_{s} & + & T_{i} . && \end{array}\end{displaymath}](img1503.gif) |
(724) |
Die kinetische Energie ist gleich der kinetischen Energie des im
Schwerpunkt vereinigt gedachten Systems, vermehrt um die kinetische Energie
der Massenpunkte bezüglich des Schwerpunktes.
Denn der 3. Term der obigen Gleichung verschwindet wegen
Z.B. ist die Gesamtenergie eines neutralen Atoms mit  Elektronen und mit
fixem Kern (der als Bezugspunkt gewählt wird) im freien Raum
Elektronen und mit
fixem Kern (der als Bezugspunkt gewählt wird) im freien Raum
Das einfachste Mehrkörperproblem ist das zweier Körper. In diesem Fall lassen
sich auch noch in einigen Fällen Lösungen angeben.
Es wird die Bewegung zweier Massen im freien Raum betrachtet. Die beiden Massen
erfahren eine Wechselwirkung, also eine Kraft, nur beim Stoß. Da dieser als
elastisch vorausgesetzt wird, gelten die Erhaltungssätze für Gesamtimpuls und
-energie. Diese lassen sich sehr zweckmäßig zur Behandlung des Problems
heranziehen. Eine weitere Vereinfachung ergibt sich, wenn man den Stoßvorgang
im Schwerpunktsystem (dort ist der Gesamtimpuls Null) betrachtet. Die
Beobachtung des physikalischen Vorganges erfolgt natürlich im Laborsystem. -
Die nachfolgende Darstellung ist
einer unveröffentlichten Arbeit von Dr. H. Neuer (mit Erlaubnis
des Autors) entnommen.
Die Koordinaten der Massen  und
und 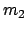 im Laborsystem (LS) und im
Schwerpunktsystem (SS) sind:
im Laborsystem (LS) und im
Schwerpunktsystem (SS) sind:
Die Umrechnung vom LS ins SS erfolgt mittels der Galileitransformation
Impulssatz im LS:
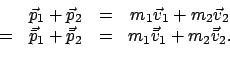 |
(726) |
Energiesatz im LS:
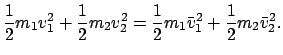 |
(727) |
Impulssatz im SS:
 |
(728) |
Energiesatz im SS:
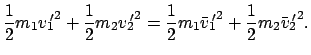 |
(729) |
Aus Gln. (7.25) und (7.28) folgt
Aus Gl. (7.28)
Abbildung:
Die Geschwindigkeiten zweier Teilchen vor und nach dem
elastischen Stoß (Zeichnung von F. Schürrer)
|
![\includegraphics[scale=0.9]{k7_elaststosz}](img1522.gif) |
folgt
und damit aus dem Energiesatz (7.29):
 |
(731) |
Im SS hat jedes Teilchen nach dem Stoß den gleichen Betrag der Geschwindigkeit
wie vor dem Stoß. Da im SS die Impulse entgegengesetzt groß sein müssen, kann
man ansetzen (s. Abb. 7.4):
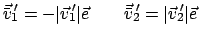 |
(732) |
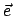 ist ein willkürlicher Einheitsvektor; er enthält 2 Freiheitsgrade,
die erst durch den eigentlichen Stoßvorgang näher bestimmt werden. Von den 6
Freiheitsgraden, die die beiden Massenpunkte
ist ein willkürlicher Einheitsvektor; er enthält 2 Freiheitsgrade,
die erst durch den eigentlichen Stoßvorgang näher bestimmt werden. Von den 6
Freiheitsgraden, die die beiden Massenpunkte
 besitzen, sind
aufgrund der 4 Erhaltungssätze (der 3 Komponenten des Gesamtimpulses und der
Gesamtenergie) nur diese 2 Freiheitsgrade übrig geblieben.
besitzen, sind
aufgrund der 4 Erhaltungssätze (der 3 Komponenten des Gesamtimpulses und der
Gesamtenergie) nur diese 2 Freiheitsgrade übrig geblieben.
Rücktransformation ins LS gibt als Resultat
Man beachte, daß der Einheitsvektor 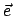 im SS bestimmt werden muß!
Die letzten beiden der obigen Gleichungen geben folgenden Sachverhalt
wieder (s. Abb. 7.3): Die Geschwindigkeit des Schwerpunkts bleibt während
des ganzen Vorgangs unverändert. Die beiden Geschwindigkeitsvektoren,
die den Einlauf der Teilchen beschreiben, spannen eine Ebene auf; die
des Auslaufes eine andere Ebene. Der elastische Stoßvorgang bewirkt
das Umschlagen von der einen Ebene in die andere. Dieser führt auch
den Vektor der anfänglichen Relativgeschwindigkeit
im SS bestimmt werden muß!
Die letzten beiden der obigen Gleichungen geben folgenden Sachverhalt
wieder (s. Abb. 7.3): Die Geschwindigkeit des Schwerpunkts bleibt während
des ganzen Vorgangs unverändert. Die beiden Geschwindigkeitsvektoren,
die den Einlauf der Teilchen beschreiben, spannen eine Ebene auf; die
des Auslaufes eine andere Ebene. Der elastische Stoßvorgang bewirkt
das Umschlagen von der einen Ebene in die andere. Dieser führt auch
den Vektor der anfänglichen Relativgeschwindigkeit
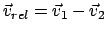 in den neuen Relativvektor
in den neuen Relativvektor
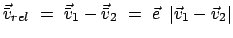 über;
der Vektor der Relativgeschwindigkeit ändert seine Richtung, nicht aber seinen Betrag.
über;
der Vektor der Relativgeschwindigkeit ändert seine Richtung, nicht aber seinen Betrag.
Abbildung:
Stoß auf ein Targetteilchen. a) Schwerpunktsystem, b) Laborsystem.
|
[]
![\includegraphics[scale=0.7]{k7_stoss_ss}](img1531.gif) []
[]
![\includegraphics[scale=0.7]{k7_stoss_ls}](img1532.gif) |
Es wird nun ein wichtiger Spezialfall weiter behandelt: 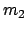 sei
vor dem Stoß in Ruhe,
sei
vor dem Stoß in Ruhe,
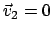 . Dann liegen die 3 Vektoren
. Dann liegen die 3 Vektoren
 wegen des Impulssatzes (7.26)
wegen des Impulssatzes (7.26)
 |
(733) |
in einer Ebene.
Wir setzen an
Damit erhält man aus Gl. (7.33) für das stoßende Teilchen
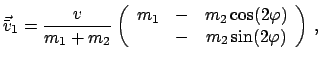 |
(734) |
und für das gestoßene Teilchen (Zielteilchen = Targetteilchen)
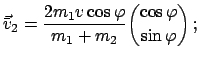 |
(735) |
2 ist der Winkel im SS (s. Abb. 7.4). Man sieht aber aus Gl. (7.35),
daß
ist der Winkel im SS (s. Abb. 7.4). Man sieht aber aus Gl. (7.35),
daß  der Ablenkwinkel für
der Ablenkwinkel für 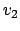 im LS ist. Der Ablenkwinkel für
im LS ist. Der Ablenkwinkel für 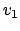 sei
sei  :
:
 |
(736) |
Bei der Inversion dieser Formel erhält man nicht den vollen Bereich
 wegen der Beschränkung des Hauptwertes des arctg. Am besten geht man von
Gl. (7.34) aus und rechnet
wegen der Beschränkung des Hauptwertes des arctg. Am besten geht man von
Gl. (7.34) aus und rechnet
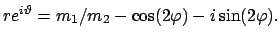 |
(737) |
Weitere Spezialisierung auf gleiche Massen gibt
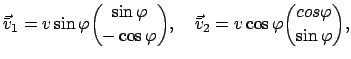 |
(738) |
Im LS stehen nach dem Stoß die beiden Geschwindigkeiten aufeinander senkrecht,
wenn
 . Es gibt keine Rückwärtsstreuung. Diese ist nur
möglich, wenn
. Es gibt keine Rückwärtsstreuung. Diese ist nur
möglich, wenn
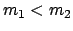 ist.
ist.
Wir wollen die vorliegende Theorie des Stoßes eines Teilchens auf ein
ruhendes noch weiterentwickeln, um den Einheitsvektor
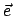 und
den Streuwinkel
und
den Streuwinkel
 aus der Stoßgeometrie zu berechnen.
Um die Berechnung ohne allzugroßen Aufwand durchführen zu können,
müssen wir voraussetzen, daß die beiden Kugeln (Masse
aus der Stoßgeometrie zu berechnen.
Um die Berechnung ohne allzugroßen Aufwand durchführen zu können,
müssen wir voraussetzen, daß die beiden Kugeln (Masse  und Radius
und Radius
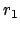 ; bzw.
; bzw. 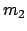 und
und 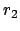 ) ideal glatt sind. Die
Stoßgeometrie ist im LS und im SS gleich, s. Abb. 7.4. Beim elastischen
Zusammenstoß der beiden ideal glatten Kugeln wird keine Energie in
Rotationsenergie umgesetzt, es werden nur die Komponenten der
Impulse
) ideal glatt sind. Die
Stoßgeometrie ist im LS und im SS gleich, s. Abb. 7.4. Beim elastischen
Zusammenstoß der beiden ideal glatten Kugeln wird keine Energie in
Rotationsenergie umgesetzt, es werden nur die Komponenten der
Impulse
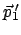 und
und
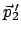 in Richtung der
Verbindungsachse
in Richtung der
Verbindungsachse 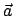 der beiden Kugelzentren umgekehrt. Dies gibt für
den Impuls der auslaufenden Kugel 1
der beiden Kugelzentren umgekehrt. Dies gibt für
den Impuls der auslaufenden Kugel 1
Abbildung:
Geometrie des Zusammenstoßes zweier Kugeln
|
![\includegraphics[scale=0.86]{k7_kugelstoss}](img1553.gif) |
mit
Wegen
ist also
Der Einheitsvektor 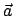 bestimmt den Vektor
bestimmt den Vektor 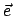 und damit den
Streuwinkel
und damit den
Streuwinkel  .
Für das behandelte ebene Problem ist das nur ein Freiheitsgrad und dieser wird
durch die Komponente von
.
Für das behandelte ebene Problem ist das nur ein Freiheitsgrad und dieser wird
durch die Komponente von 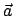 senkrecht zu
senkrecht zu
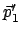 (oder
(oder
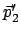 )
bestimmt. Diese hängt ihrerseits von den beiden Kugelradien und vom Abstand
)
bestimmt. Diese hängt ihrerseits von den beiden Kugelradien und vom Abstand
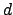 der beiden Zentren im Augenblick des Zusammenstoßes ab (7.5):
der beiden Zentren im Augenblick des Zusammenstoßes ab (7.5):
Für
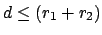 ist
ist
Aus Gl. (7.39) erhält man für den Winkel  , um den die vor dem Stoß
ruhende Masse
, um den die vor dem Stoß
ruhende Masse 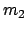 abgelenkt wird:
Der Streuwinkel
abgelenkt wird:
Der Streuwinkel  der einlaufenden Masse
der einlaufenden Masse 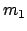 wird aus Gl. (7.37)
berechnet. Für
wird aus Gl. (7.37)
berechnet. Für
 findet kein Stoß statt:
In Abb. 7.6 werden die Streuwinkel als Funktion des relativen Abstandes der
beiden Kugeln gezeigt. Die einlaufende Masse
findet kein Stoß statt:
In Abb. 7.6 werden die Streuwinkel als Funktion des relativen Abstandes der
beiden Kugeln gezeigt. Die einlaufende Masse 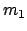 kann nach rückwärts
gestreut werden, wenn sie leichter als das Target
kann nach rückwärts
gestreut werden, wenn sie leichter als das Target 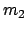 , sonst nicht.
, sonst nicht.
Zur Behandlung des Zweikörperproblems ohne äußere Kräfte gibt es einen
Satz von Koordinaten, der vorteilhafter ist als die Koordinaten relativ zum
Schwerpunkt, wie sie in Gl. (7.23) eingeführt worden sind. Diese
günstigeren Koordinaten sind die
Lage des Schwerpunktes
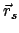 und der relative Abstand
und der relative Abstand 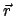 der
beiden Massenpunkte.
der
beiden Massenpunkte.
Abbildung:
Schwerpunkts- und Relativkoordinate im Zweikörperproblem
|
![\includegraphics[scale=0.8]{k7_relativ_schwerpkt_koord}](img1573.gif) |
Ist eine der Massen, 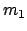 (Sonne), wesentlich schwerer als die andere,
(Sonne), wesentlich schwerer als die andere, 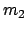 (Planet), dann unterscheidet sich
(Planet), dann unterscheidet sich
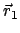 nur wenig von
nur wenig von
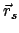 ;
und
;
und 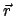 ist fast derRadiusvektor von der Sonne zum Planeten.
ist fast derRadiusvektor von der Sonne zum Planeten.
Aus den Bewegungsgleichungen für die beiden Massenpunkte folgt durch Addition
die Bewegungsgleichung für den Schwerpunkt (vgl. Gln. (7.4) - (7.8)):
Setzt man Gln. (7.42) in die obigen Bewegungsgleichungen für
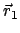 bzw.
bzw.
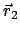 ein, dann ergibt sich in beiden Fällen dieselbe Gleichung:
ein, dann ergibt sich in beiden Fällen dieselbe Gleichung:
![\begin{displaymath}\begin{array}{\vert ccc\vert} \hline && [-0.5em]\mu \ddot...
...) < m_{2} \leq m_{1}. [-0.5em]&& \hline \end{array}\end{displaymath}](img1587.gif) |
(743) |
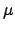 heißt die reduzierte Masse. Durch die Einführung der Koordinaten
heißt die reduzierte Masse. Durch die Einführung der Koordinaten
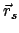 und
und
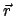 wird das Problem der relativen Bewegung zweier Massen in ein fiktives
Einkörperproblem verwandelt, in dem die reduzierte Masse die Rolle der
Einteilchenmasse und das Wechselwirkungspotential die Rolle des Potentials
einer ''fiktiven äußeren Kraft'' spielen.
wird das Problem der relativen Bewegung zweier Massen in ein fiktives
Einkörperproblem verwandelt, in dem die reduzierte Masse die Rolle der
Einteilchenmasse und das Wechselwirkungspotential die Rolle des Potentials
einer ''fiktiven äußeren Kraft'' spielen.
Einsetzen der Substitutionen (7.42) in den Ausdruck für die kinetische Energie
ergibt:
![\begin{displaymath}\begin{array}{ccccc} T = \frac{m_{1}}{2} \dot{\vec r}_{1}...
...} \vec v^{ 2} , [1mm] & = & T_{s} & + & T_{i} . \end{array}\end{displaymath}](img1588.gif) |
(744) |
Die kinetische Energie des Schwerpunktes 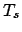 ist bei Fehlen äußerer
Kräfte konstant und kann daher weggelassen werden, wenn nur die innere Bewegung des
Systems interessiert. Dann lautet der Energiesatz
ist bei Fehlen äußerer
Kräfte konstant und kann daher weggelassen werden, wenn nur die innere Bewegung des
Systems interessiert. Dann lautet der Energiesatz
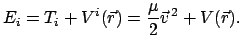 |
(745) |
Ist die Kraft zwischen den beiden Massenpunkten eine Zentralkraft, dann ist
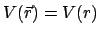 .
Daher können wir sofort die Lösung des Keplerproblems für unendlich schwere
Zentralmasse aus §5.2 übernehmen. Dabei bleibt die Konstante
.
Daher können wir sofort die Lösung des Keplerproblems für unendlich schwere
Zentralmasse aus §5.2 übernehmen. Dabei bleibt die Konstante 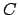 in Gl. (5.15) unverändert. Die Masse
in Gl. (5.15) unverändert. Die Masse  ist sonst überall durch
ist sonst überall durch 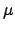 zu ersetzen
zu ersetzen
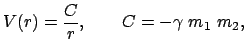
oder
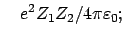
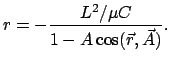 |
(746) |
Als erste Anwendung betrachten wir ein isoliertes Zweikörperproblem
(Doppelsternsystem). Das relative Verhältnis der beiden Massen ist für
die nachfolgende Betrachtung der Keplerschen Gesetze unwesentlich.
- Jeder der beiden Körper bewegt sich längs eines ähnlichen Kegelschnittes
um den gemeinsamen Schwerpunkt (= Brennpunkt jedes
Kegelschnittes), s. Notebook: K7Doppelst.nb.
- Der Flächensatz gilt auch hier: Dabei bestimmen die relative Position und
die Geschwindigkeit der beiden Massenpunkte die Flächengeschwindigkeit.
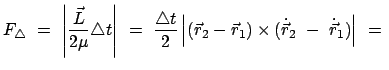 const. const. |
(747) |
- Für das dritte Keplersche Gesetz berechnet man analog wie in
Gl. (3.41), (vgl. §5.2.3)
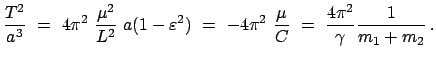 |
(748) |
Beide Körper haben die gleiche Umlaufdauer 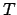 auf ihrer jeweiligen Bahn;
auf ihrer jeweiligen Bahn;
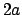 ist ihr maximaler Abstand.
ist ihr maximaler Abstand.
Für das Planetensystem kann das obige Resultat nur in einer Näherung benützt
werden: Die Anziehung der Planeten untereinander wird vernachlässigt gegenüber
der Kraft der Sonne (Masse 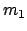 ). Für
). Für 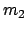 wird die Masse des jeweils
betrachteten Planeten eingesetzt. Dieses Näherungsverfahren ist nur sinnvoll, wenn die
Zentralmasse
wird die Masse des jeweils
betrachteten Planeten eingesetzt. Dieses Näherungsverfahren ist nur sinnvoll, wenn die
Zentralmasse 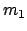 groß ist im Vergleich zur Masse aller Planeten. Dann ergibt
sich für die Keplerschen Gesetze:
groß ist im Vergleich zur Masse aller Planeten. Dann ergibt
sich für die Keplerschen Gesetze:
- Bei Vernachlässigung der gegenseitigen Anziehung der Planeten untereinander
und ihrer Wechselwirkung über die Sonne, bewegen sich die Sonne und der
betrachtete Planet auf ähnlichen Kegelschnitten um den gemeinsamen Schwerpunkt.
Für
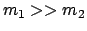 ist
ist 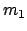 fast in Ruhe.
fast in Ruhe.
Im Sonnensystem ist Jupiter der schwerste Planet, Saturn der zweitschwerste.
Unter der Annahme, daß jeweils nur einer dieser beiden Planeten um die Sonne
kreist, ergeben sich aus Gl. (7.40) folgende Werte für die mittleren Bahnradien
Vergleicht man diese mit dem Wert des Sonnenradius
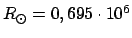 km, sieht
man, daß der gemeinsame Schwerpunkt des Systems Sonne - Jupiter (Saturn) in der
Sonnenkorona liegt.
km, sieht
man, daß der gemeinsame Schwerpunkt des Systems Sonne - Jupiter (Saturn) in der
Sonnenkorona liegt.
- Der Flächensatz gilt nur näherungsweise unter den Voraussetzungen wie in 1.
- Es folgt aus Gl. (7.48)
Die Umlaufzeiten aller Planeten gehorchen dem 3. Keplerschen Gesetz nur dann,
wenn die Gesamtheit ihrer Massen klein ist gegen die Zentralmasse
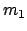 .
.
Christian Sommer
2003-01-27
![]() Massenpunkten. Der
Massenpunkten. Der ![]() -te Massenpunkt hat die
Masse
-te Massenpunkt hat die
Masse ![]() . Seine augenblickliche Lage wird durch den Vektor
. Seine augenblickliche Lage wird durch den Vektor
![]() angegeben,
s. Abb. 7.1(a). Die Bewegung des
angegeben,
s. Abb. 7.1(a). Die Bewegung des ![]() -ten
Massenpunktes wird durch die Newtonsche
Bewegungsgleichung beschrieben:
-ten
Massenpunktes wird durch die Newtonsche
Bewegungsgleichung beschrieben:
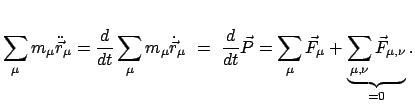
![]() sind), dann gilt der Erhaltungssatz des
Impulses und des Anfangsschwerpunktes:
sind), dann gilt der Erhaltungssatz des
Impulses und des Anfangsschwerpunktes:
![]() äußerlich
multipliziert und das Produkt über
äußerlich
multipliziert und das Produkt über ![]() summiert. Dies gibt
summiert. Dies gibt
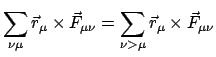
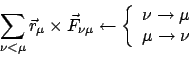
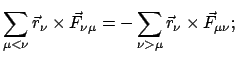

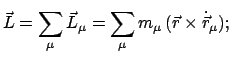
![]() im Abstand
im Abstand
![]() (Abb. 7.2(a))
über, ergibt einfache Ausrechnung:
(Abb. 7.2(a))
über, ergibt einfache Ausrechnung:
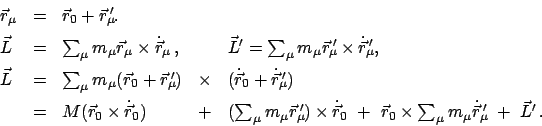
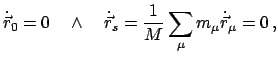
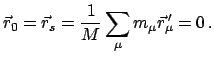
![]() innerlich multipliziert,
das Produkt über
innerlich multipliziert,
das Produkt über ![]() summiert. Der Ausdruck auf der linken Seite ist die gesamte kinetische
Energie
summiert. Der Ausdruck auf der linken Seite ist die gesamte kinetische
Energie ![]() :
:
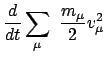
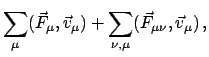

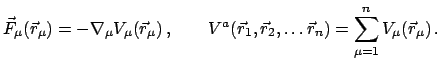
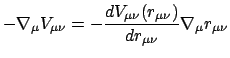
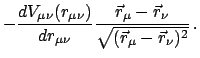
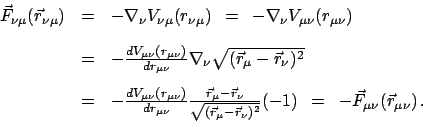

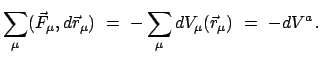
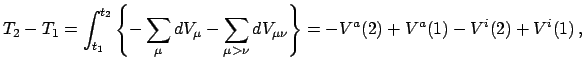
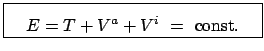
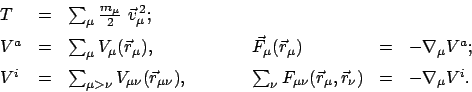
![\begin{displaymath}\begin{array}{ccccccccc} T & = & \sum_{\mu} \frac{m_{\mu}}{2}...
...}^{2} && [1em] &&& = & T_{s} & + & T_{i} . && \end{array}\end{displaymath}](img1503.gif)
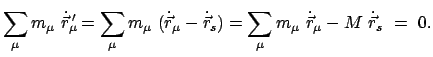
![]() Elektronen und mit
fixem Kern (der als Bezugspunkt gewählt wird) im freien Raum
Elektronen und mit
fixem Kern (der als Bezugspunkt gewählt wird) im freien Raum
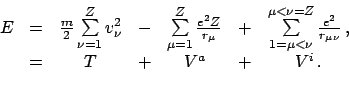
![]() und
und ![]() im Laborsystem (LS) und im
Schwerpunktsystem (SS) sind:
im Laborsystem (LS) und im
Schwerpunktsystem (SS) sind:
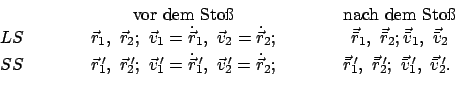
![\includegraphics[scale=0.9]{k7_elaststosz}](img1522.gif)
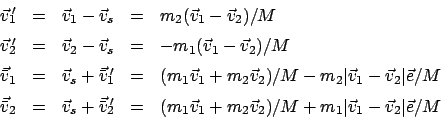
![]() sei
vor dem Stoß in Ruhe,
sei
vor dem Stoß in Ruhe,
![]() . Dann liegen die 3 Vektoren
. Dann liegen die 3 Vektoren
![]() wegen des Impulssatzes (7.26)
wegen des Impulssatzes (7.26)


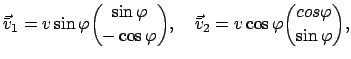
![]() und
den Streuwinkel
und
den Streuwinkel
![]() aus der Stoßgeometrie zu berechnen.
Um die Berechnung ohne allzugroßen Aufwand durchführen zu können,
müssen wir voraussetzen, daß die beiden Kugeln (Masse
aus der Stoßgeometrie zu berechnen.
Um die Berechnung ohne allzugroßen Aufwand durchführen zu können,
müssen wir voraussetzen, daß die beiden Kugeln (Masse ![]() und Radius
und Radius
![]() ; bzw.
; bzw. ![]() und
und ![]() ) ideal glatt sind. Die
Stoßgeometrie ist im LS und im SS gleich, s. Abb. 7.4. Beim elastischen
Zusammenstoß der beiden ideal glatten Kugeln wird keine Energie in
Rotationsenergie umgesetzt, es werden nur die Komponenten der
Impulse
) ideal glatt sind. Die
Stoßgeometrie ist im LS und im SS gleich, s. Abb. 7.4. Beim elastischen
Zusammenstoß der beiden ideal glatten Kugeln wird keine Energie in
Rotationsenergie umgesetzt, es werden nur die Komponenten der
Impulse
![]() und
und
![]() in Richtung der
Verbindungsachse
in Richtung der
Verbindungsachse ![]() der beiden Kugelzentren umgekehrt. Dies gibt für
den Impuls der auslaufenden Kugel 1
der beiden Kugelzentren umgekehrt. Dies gibt für
den Impuls der auslaufenden Kugel 1
![\begin{displaymath}
\begin{array}{lclcl}
\vec p_{1}{\hspace{-1mm}'} & = & \quad ...
...a) -
\frac{\vec{v}_{1}{\hspace{-1mm}'}}{v_{1}}\big]
\end{array}\end{displaymath}](img1554.gif)
![]() bestimmt den Vektor
bestimmt den Vektor ![]() und damit den
Streuwinkel
und damit den
Streuwinkel ![]() .
Für das behandelte ebene Problem ist das nur ein Freiheitsgrad und dieser wird
durch die Komponente von
.
Für das behandelte ebene Problem ist das nur ein Freiheitsgrad und dieser wird
durch die Komponente von ![]() senkrecht zu
senkrecht zu
![]() (oder
(oder
![]() )
bestimmt. Diese hängt ihrerseits von den beiden Kugelradien und vom Abstand
)
bestimmt. Diese hängt ihrerseits von den beiden Kugelradien und vom Abstand
![]() der beiden Zentren im Augenblick des Zusammenstoßes ab (7.5):
der beiden Zentren im Augenblick des Zusammenstoßes ab (7.5):
![]() ist
ist
![]() und der relative Abstand
und der relative Abstand ![]() der
beiden Massenpunkte.
der
beiden Massenpunkte.
![]() (Sonne), wesentlich schwerer als die andere,
(Sonne), wesentlich schwerer als die andere, ![]() (Planet), dann unterscheidet sich
(Planet), dann unterscheidet sich
![]() nur wenig von
nur wenig von
![]() ;
und
;
und ![]() ist fast derRadiusvektor von der Sonne zum Planeten.
ist fast derRadiusvektor von der Sonne zum Planeten.
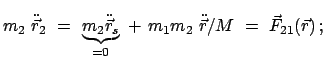
![\begin{displaymath}\begin{array}{\vert ccc\vert} \hline && [-0.5em]\mu \ddot...
...) < m_{2} \leq m_{1}. [-0.5em]&& \hline \end{array}\end{displaymath}](img1587.gif)
![]() heißt die reduzierte Masse. Durch die Einführung der Koordinaten
heißt die reduzierte Masse. Durch die Einführung der Koordinaten
![]() und
und
![]() wird das Problem der relativen Bewegung zweier Massen in ein fiktives
Einkörperproblem verwandelt, in dem die reduzierte Masse die Rolle der
Einteilchenmasse und das Wechselwirkungspotential die Rolle des Potentials
einer ''fiktiven äußeren Kraft'' spielen.
wird das Problem der relativen Bewegung zweier Massen in ein fiktives
Einkörperproblem verwandelt, in dem die reduzierte Masse die Rolle der
Einteilchenmasse und das Wechselwirkungspotential die Rolle des Potentials
einer ''fiktiven äußeren Kraft'' spielen.
![\begin{displaymath}\begin{array}{ccccc} T = \frac{m_{1}}{2} \dot{\vec r}_{1}...
...} \vec v^{ 2} , [1mm] & = & T_{s} & + & T_{i} . \end{array}\end{displaymath}](img1588.gif)
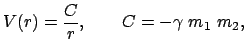 oder
oder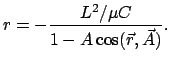
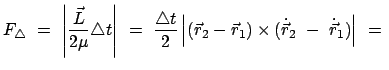 const.
const.