Unterabschnitte
Prinzipe der Mechanik
In diesem Kapitel werden einige verschiedene, mit den Newtonschen Axiomen (und
Bewegungsgleichungen) äquivalente Axiome oder Grundgleichungen (= Prinzipe)
zur Beschreibung der mechanischen Vorgänge behandelt. Als erstes wird
das Prinzip der virtuellen Verrückungen vorgestellt; es dient zur Bestimmung
des Gleichgewichts statischer Systeme. Dieses Prinzip wird dann verallgemeinert
zum d'Alembertschen Prinzip; damit kann man Bewegungsgleichungen erhalten;
insbesondere werden die Lagrangeschen Gleichungen 1. Art nochmals abgeleitet.
Ein grosser Vorteil mancher dieser Prinzipe ist es, dass diese in einer Form
ausgedrückt werden können, die von den Koordinaten unabhängig ist. Diese
Eigenschaft kommt insbesondere der Lagrangeschen Zentralgleichung, einem
Differentialprinzip, und dem Hamiltonschen Prinzip, einem Integralprinzip, zu.
Mit Ihrer Hilfe ist es dann möglich, die Bewegungsgleichungen in krummlinigen
Koordinatensystemen, die Lagrangeschen Gleichungen 2. Art, abzuleiten. -
Das Hamiltonsche Prinzip gestattet es, den Zusammenhang zwischen Symmetrien
eines Systems und dessen Erhaltungsgrößen aufzuzeigen.
Dieses Prinzip liefert eine Bedingung für das Gleichgewicht eines
mechanischen Systems. Es wird zuerst an einem freien System, bestehend aus
einem Massenpunkt, erläutert.
Gleichgewicht liegt vor, wenn die Resultierende, 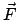 , der auf den Massenpunkt
wirkenden Kräfte Null ist. Diese Bedingung wird nun umformuliert, indem man die
drei Komponenten der Gleichung
, der auf den Massenpunkt
wirkenden Kräfte Null ist. Diese Bedingung wird nun umformuliert, indem man die
drei Komponenten der Gleichung
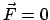 jeweils mit den willkürlichen
infinitesimalen Faktoren
jeweils mit den willkürlichen
infinitesimalen Faktoren
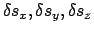 multipliziert und addiert. Nimmt man an, daß diese Faktoren die Dimension
einer Länge haben, dann erhält der
folgende so gewonnene Summenausdruck die Dimension einer Arbeit
multipliziert und addiert. Nimmt man an, daß diese Faktoren die Dimension
einer Länge haben, dann erhält der
folgende so gewonnene Summenausdruck die Dimension einer Arbeit
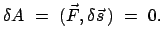 |
(111) |
Umgekehrt folgt das Verschwinden der Kraft aus
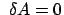 ,
,
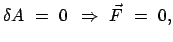 |
(112) |
da
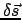 vollkommen willkürlich ist. (Die Willkürlichkeit ist
wichtig, denn sonst wäre
der Fall
vollkommen willkürlich ist. (Die Willkürlichkeit ist
wichtig, denn sonst wäre
der Fall
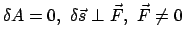 möglich).
möglich).
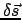 heißt virtuelle
(d.i. gedachte) Verrückung (E.: virtual displacement). Gl. (11.1)
ist das Prinzip der virtuellen Verrückung
oder das Prinzip der virtuellen Arbeit. Es bietet den Vorteil,
3 Vektorgleichungen in eine skalare Gleichung zusammenzufassen.
heißt virtuelle
(d.i. gedachte) Verrückung (E.: virtual displacement). Gl. (11.1)
ist das Prinzip der virtuellen Verrückung
oder das Prinzip der virtuellen Arbeit. Es bietet den Vorteil,
3 Vektorgleichungen in eine skalare Gleichung zusammenzufassen.
Als nächstes betrachten wir ein gebundenes System, bestehend aus einem
Massenpunkt. Hier beschränken Nebenbedingungen die Beweglichkeit des
Massenpunktes.
Diese werden in den Bewegungsgleichungen durch die Einführung von
Zwangskräften (Reaktionskräften) als Zusatzkräfte berücksichtigt.
Dadurch erhält man wieder ein fiktives freies System mit den
Bewegungsgleichungen
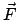 eingeprägte Kraft,
eingeprägte Kraft, 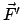 Zwangskraft. Letztere steht senkrecht
auf den Flächen oder Kurven, die als Führungen die Bewegung beschränken.
Nun hat man die Bedingung:
Zwangskraft. Letztere steht senkrecht
auf den Flächen oder Kurven, die als Führungen die Bewegung beschränken.
Nun hat man die Bedingung:
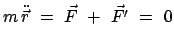 |
(113) |
Hier kann durchaus
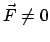 sein. Hier erfolgen die virtuellen
Verrückungen nur mehr in Richtung der Führungen. Genauer: Die infinitesimalen
virtuellen Verrückungen
sein. Hier erfolgen die virtuellen
Verrückungen nur mehr in Richtung der Führungen. Genauer: Die infinitesimalen
virtuellen Verrückungen
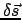 erfolgen nur mehr in Richtung der
Tangentialebene bzw. Tangente an die Führung. Die Zwangskräfte stehen auf diesen
senkrecht, s. Gl. (6.4).
erfolgen nur mehr in Richtung der
Tangentialebene bzw. Tangente an die Führung. Die Zwangskräfte stehen auf diesen
senkrecht, s. Gl. (6.4).
 |
(114) |
Die Bedingung für Gleichgewicht ist also:
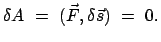 |
(115) |
Daraus folgt nicht unbedingt, daß
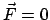 , da
, da
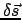 nicht mehr
vollständig willkürlich ist.
nicht mehr
vollständig willkürlich ist.
Abbildung 11.1:
Ein homogener Stab lehnt an einer Wand.
|
|
Dieses Prinzip wird nun an einem Beispiel vorgeführt. Ein Stab der Länge 2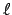 lehnt an einer Wand. Es sei keine Reibung an den Auflageflächen vorhanden. Wie
groß muß die Kraft
lehnt an einer Wand. Es sei keine Reibung an den Auflageflächen vorhanden. Wie
groß muß die Kraft 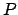 sein, damit der Stab nicht unter seinem Gewicht
sein, damit der Stab nicht unter seinem Gewicht 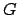 wegrutscht? (s. Abb. 11.1). Man kann annehmen, daß alle Kräfte im
Schwerpunkt
wegrutscht? (s. Abb. 11.1). Man kann annehmen, daß alle Kräfte im
Schwerpunkt  angreifen. Das Prinzip der virtuellen Arbeit gibt:
angreifen. Das Prinzip der virtuellen Arbeit gibt:
Die beiden Komponenten 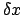 und
und 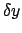 der Verrückung
der Verrückung
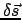 sind voneinander abhängig. Die Änderung
sind voneinander abhängig. Die Änderung
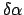 des
Neigungswinkels
des
Neigungswinkels 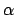 ist ein freier Parameter.
Die virtuelle Verrückung längs der Tangente an den Kreis
ist ein freier Parameter.
Die virtuelle Verrückung längs der Tangente an den Kreis
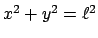 gibt für die virtuelle Arbeit und damit für
gibt für die virtuelle Arbeit und damit für 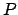 :
Die resultierende gesamte Kraft weist immer auf die Kante Boden - Mauer (Abb. 11.1)
:
Die resultierende gesamte Kraft weist immer auf die Kante Boden - Mauer (Abb. 11.1)
Für ein freies oder gebundenes System von 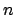 Massenpunkten gelten die
Bewegungsgleichungen
Massenpunkten gelten die
Bewegungsgleichungen
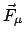 eingeprägte,
eingeprägte,
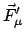 Zwangskräfte. Die Bedingung
für Gleichgewicht ist
Zwangskräfte. Die Bedingung
für Gleichgewicht ist
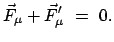 |
(116) |
Die virtuellen Verrückungen
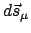 werden wieder so gewählt,
daß sie mit den Nebenbedingungen verträglich sind
werden wieder so gewählt,
daß sie mit den Nebenbedingungen verträglich sind
Ein System ist in Ruhe oder Gleichgewicht, wenn die potentielle Energie ein
Extremum oder einen Sattelpunkt hat. Bei einer kleinen Verrückung dürfen die
eingeprägten Kräfte keine Arbeit leisten, da sie sonst das System in Bewegung
setzen würden. Daher lautet die Bedingung für Gleichgewicht
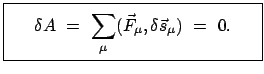 |
(117) |
Dies ist das Prinzip der virtuellen Verrückungen
(Johann Bernoulli, 1717). Ist
das System frei:
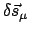 beliebig, so folgt
beliebig, so folgt
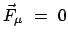 ;
ist das System gebunden,
dann sind die
;
ist das System gebunden,
dann sind die
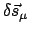 nicht völlig willkürlich (sie müssen
mit den Nebenbedingungen verträglich sein),
nicht völlig willkürlich (sie müssen
mit den Nebenbedingungen verträglich sein),
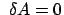 , aber meist
, aber meist
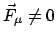 .
.
Das Prinzip der virtuellen Verrückungen, Gl. (11.5), gilt nur für statische
Systeme, es ist für dynamische, also für Bewegungsvorgänge, nicht
verwendbar. Seine Fortentwicklung für dynamische Vorgänge heißt das
Prinzip von d'Alembert.
Dazu wird die Bewegungsgleichung formal in eine Gleichung verwandelt, in der
nur Kräfte aufscheinen; auf diese wird dann das Prinzip der virtuellen
Verrückung angewendet. Dazu wird in die Bewegungsgleichung die d'Alembertsche
Trägheitskraft eingeführt
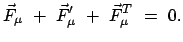 |
(118) |
Eine mit den Nebenbedingungen verträgliche Verrückung,
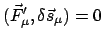 , gibt dann
, gibt dann
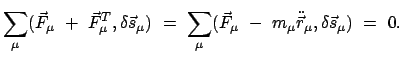 |
|
|
(119) |
Dies ist das Prinzip von d'Alembert (1743), (Lagrange 1788).
Für das Weitere wird nun eine neue Schreibweise eingeführt:
Damit lautet dann das Prinzip von d'Alembert:
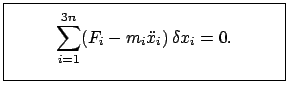 |
(1110) |
Die allgemeinste Form einer Nebenbedingung ist
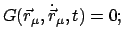 |
(1111) |
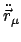 darf nicht vorkommen, sonst wäre Gl. (11.11) eine die
Bewegungsgleichung konkurrierende Bedingung.
darf nicht vorkommen, sonst wäre Gl. (11.11) eine die
Bewegungsgleichung konkurrierende Bedingung.
Abbildung 11.2:
Bewegung einer Schneide.
|
|
Gl. (11.11) ist eine Differentialgleichung. Eine solche
Nebenbedingung tritt z.B. bei der Beschreibung der Bewegung einer Schneide eines
Schlittschuhs auf ebenem Eis auf: Zwei Punkte sind durch eine feste Stange der
Länge 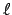 verbunden und werden gezwungen, sich in einer solchen Weise zu
bewegen, daß die Geschwindigkeit des Mittelpunktes der Stange in Richtung der
Stange liegt (Abb. 11.2). Dies gibt die beiden Nebenbedingungen
verbunden und werden gezwungen, sich in einer solchen Weise zu
bewegen, daß die Geschwindigkeit des Mittelpunktes der Stange in Richtung der
Stange liegt (Abb. 11.2). Dies gibt die beiden Nebenbedingungen
Aus der zweiten Gleichung eliminiert man den unbekannten Parameter 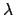 ,
indem man die
,
indem man die 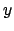 -Komponente durch die
-Komponente durch die 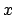 -Komponente dividiert.
-Komponente dividiert.
Tritt keine Ableitung in der Nebenbedingung auf, dann heißt diese holonom.
Enthält sie aber noch die Zeit, dann heißt sie rheonom. Kommt auch die
Zeit nicht
vor, dann heißt die Bedingung skleronom. Alle diese Bezeichnungen werden
nochmals zusammengefaßt:
Die Form der Bewegungsgleichungen bei Bestehen von einschränkenden
Nebenbedingungen ist in §6.1 mittels physikalischer Überlegungen
abgeleitet worden. Hier werden wir sie mit Hilfe des d'Alembertschen Prinzips
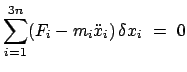 |
(1112) |
aufsuchen. Darin sind wegen der Nebenbedingungen nicht mehr alle
 unabhängig. Diese Abhängigkeit kann man angeben, wenn man die
skleronomen Nebenbedingungen
unabhängig. Diese Abhängigkeit kann man angeben, wenn man die
skleronomen Nebenbedingungen
 |
(1113) |
(m = 3n gäbe ebensoviele Nebenbedingungen wie Koordinaten; der Massenpunkt
könnte sich überhaupt nicht mehr bewegen) variiert
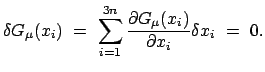 |
(1114) |
Aufgrund der Nebenbedingungen (11.13) sind nur mehr 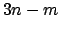 der
der
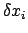 , z.B. die letzten
, z.B. die letzten 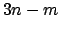 der
der
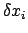 , voneinander
unabhängig; die übrigen, in unserem Beispiel die ersten
, voneinander
unabhängig; die übrigen, in unserem Beispiel die ersten
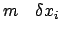 , hängen von den unabhängigen
, hängen von den unabhängigen
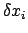 (im Beispiel von den letzten
(im Beispiel von den letzten
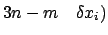 ab.
Daher kann im d'Alembertschen Prinzip, Gl. (11.12),
nicht gefolgert werden, daß der Koeffizient
ab.
Daher kann im d'Alembertschen Prinzip, Gl. (11.12),
nicht gefolgert werden, daß der Koeffizient
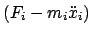 jedes
jedes
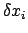 Null ist. Es gibt nun 2 Verfahren, diese Schwierigkeiten zu beheben:
Null ist. Es gibt nun 2 Verfahren, diese Schwierigkeiten zu beheben:
- Elimination der abhängigen
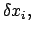
- Die Methode der Lagrangeschen Multiplikatoren.
Verfahren 1. wird am Beispiel einer Bewegung in zwei Dimensionen vorgeführt:
Da 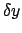 willkürlich ist, muß der Ausdruck in der rechteckigen
Klammer Null sein; dies ist aber eine komplizierte Gleichung.
Deswegen bevorzugt man das zweite Verfahren.
willkürlich ist, muß der Ausdruck in der rechteckigen
Klammer Null sein; dies ist aber eine komplizierte Gleichung.
Deswegen bevorzugt man das zweite Verfahren.
Beim Verfahren der Lagrangeschen Multiplikatoren (E. Lagrange multipliers)
werden die Gln. (11.14) mit
zunächst willkürlichen Faktoren
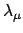 multipliziert,
über
multipliziert,
über 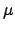 summiert und dann zu (11.12) addiert:
summiert und dann zu (11.12) addiert:
![$\displaystyle \sum_{i=1}^{3n} \left[ F_{i} - m_{i} \ddot{x}_{i} + \sum_{\mu...
...bda_{\mu} \frac{\partial G_{\mu}}{\partial x_{i}} \right] \delta x_{i} = 0.$](img3015.gif) |
(1115) |
In dieser Gleichung werden die
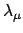 so gewählt, daß die ersten
so gewählt, daß die ersten  Klammerausdrücke (
Klammerausdrücke (
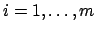 ) Null sind. Die verbleibende Summe
läuft nur mehr von
) Null sind. Die verbleibende Summe
läuft nur mehr von
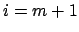 bis
bis 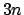 und enthält dann nur mehr
und enthält dann nur mehr
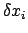 , die voneinander
unabhängig sind. Diese Summe
kann also nur Null sein, wenn der Koeffizient jedes
, die voneinander
unabhängig sind. Diese Summe
kann also nur Null sein, wenn der Koeffizient jedes
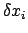 ,
also die Ausdrücke in den rechteckigen Klammern zu
,
also die Ausdrücke in den rechteckigen Klammern zu
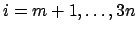 Null sind.
Dies gibt die Lagrangeschen Gleichungen 1. Art:
Null sind.
Dies gibt die Lagrangeschen Gleichungen 1. Art:
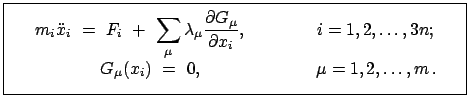 |
(1116) |
Zusammen sind dies 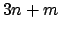 Gleichungen für die
Gleichungen für die 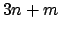 unbekannten Funktionen
unbekannten Funktionen
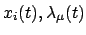 . Der zweite Term auf der rechten Seite von
Gl. (11.16) gibt die Zwangskräfte.
. Der zweite Term auf der rechten Seite von
Gl. (11.16) gibt die Zwangskräfte.
Die Lagrangesche Zentralgleichung und die Lagrangeschen Gleichungen
zweiter Art
Die Lösung der Lagrangeschen Gleichungen erster Art, Gln. (11.16),
wird oft dadurch erschwert, daß es schwierig ist, Lösungen dieser
Gleichungen zu finden, die
auch die Nebenbedingungen erfüllen. Oft ist es günstiger,
den Zwangsbedingungen
angepaßte krummlinige Koordinaten einzuführen, sodaß sich die
Zwangsbedingungen
in der Konstanz eines Teiles dieser Koordinaten ausdrücken lassen.
Man erhält damit eine geringere Anzahl von veränderlichen Koordinaten, eben
nur mehr soviel als den vorhandenen Bewegungsmöglichkeiten entspricht. Auch
bei freien Systemen ist es oft zweckmäßig, der Symmetrie des Systems angepaßte,
krummlinige Koordinaten zu verwenden. Die Bewegungsgleichungen in krummlinigen
Koordinatensystemen sind die Lagrangeschen Gleichungen zweiter Art.
Diese werden aus dem d'Alembertschen Prinzip
abgeleitet werden. Dabei ist es wichtig, den Unterschied zwischen 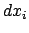 und
und
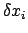 zu beachten, (Abb. 11.3):
zu beachten, (Abb. 11.3):
Abbildung 11.3:
Differential und Variationsinkrement
|
|
Das Differential
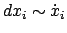 liegt in Richtung der Tangente an
die Raumkurve
liegt in Richtung der Tangente an
die Raumkurve 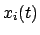 ;
;
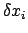 ist ein willkürliches Inkrement.
Deswegen ist es nicht von
vorneherein klar, ob man in dem zweiten Term der rechten Seite des Ausdruckes
ist ein willkürliches Inkrement.
Deswegen ist es nicht von
vorneherein klar, ob man in dem zweiten Term der rechten Seite des Ausdruckes
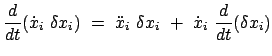 |
(1117) |
die Symbole 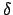 und
und 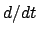 vertauschen darf. Dazu betrachten wir
vertauschen darf. Dazu betrachten wir
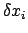 als
Differenz der gleichen Zeiten
als
Differenz der gleichen Zeiten  entsprechenden Punkte
entsprechenden Punkte 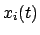 und
und
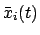 zweier Raumkurven, Abb. 11.3.
zweier Raumkurven, Abb. 11.3.
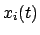 als Funktion von
als Funktion von  gibt die tatsächliche Bahn,
gibt die tatsächliche Bahn,
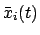 ist die variierte Vergleichsbahn. Die Zeitableitung der Variation
ist die variierte Vergleichsbahn. Die Zeitableitung der Variation
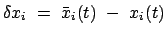 |
(1118) |
ist
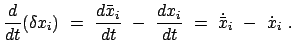 |
(1119) |
Andererseits folgt aus der Bedeutung des Zeichens 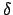 :
:
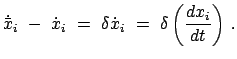 |
(1120) |
Vergleich der beiden vorhergehenden Gleichungen gibt das gesuchte Endresultat:
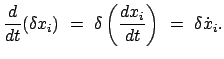 |
(1121) |
Die wesentliche Voraussetzung für den Beweis der Formel (11.21) ist die Existenz
der Differenz
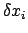 , Gl. (11.18). - Die Gln. (11.18)
und (11.21) gelten nicht bei
den sogenannten ''Quasikoordinaten''; letztere werden über die
Geschwindigkeiten oder Differentiale definiert:
, Gl. (11.18). - Die Gln. (11.18)
und (11.21) gelten nicht bei
den sogenannten ''Quasikoordinaten''; letztere werden über die
Geschwindigkeiten oder Differentiale definiert:
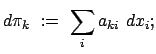 |
(1122) |
zu diesen Differentialausdrücken existieren keine entsprechenden
holonomen (''integrierten'') Gleichungen, wenn die Koeffizienten 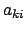 in
(11.22) die Integrabilitätsbedingungen
nicht erfüllen. - Beispiele solcher Quasikoordinaten sind die Komponenten des
Vektors
in
(11.22) die Integrabilitätsbedingungen
nicht erfüllen. - Beispiele solcher Quasikoordinaten sind die Komponenten des
Vektors
 der Winkelgeschwindigkeit, Gln. (8.22) und
(8.30).
der Winkelgeschwindigkeit, Gln. (8.22) und
(8.30).
Gl. (11.21) wird auf Gl. (11.17) angewendet, diese dann in
Gl. (11.12) eingesetzt. Dies gibt
Der erste Ausdruck der linken Seite ist die variierte Arbeit; der zweite gibt
die Variation der kinetischen Energie
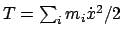 , wenn
man das
Variationszeichen vor die Summe zieht. Als Resultat der Umrechnung erhält man
die Lagrangesche Zentralgleichung.
, wenn
man das
Variationszeichen vor die Summe zieht. Als Resultat der Umrechnung erhält man
die Lagrangesche Zentralgleichung.
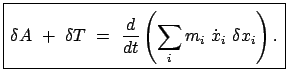 |
(1123) |
Man beachte, daß auf der linken Seite nur mehr koordinatenvariante Größen stehen.
Dies ist der Vorteil dieser Gleichung.
Wir gehen nun über auf neue (meist krummlinige) Koordinaten 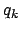 durch die
Transformationen
durch die
Transformationen
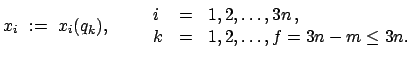 |
(1124) |
Diese sollen so beschaffen sein, daß etwa vorhandene Nebenbedingungen
für beliebige Werte der 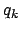 identisch befriedigt sind. Die Zahl der
unabhängigen Variablen
identisch befriedigt sind. Die Zahl der
unabhängigen Variablen 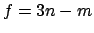 (= mechanischer Freiheitsgrad)
(E.: mechanical degree of freedom) ist kleiner als
(= mechanischer Freiheitsgrad)
(E.: mechanical degree of freedom) ist kleiner als
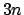 , weil die Nebenbedingungen eliminiert worden sind. Bei Fehlen von
Nebenbedingungen ist
, weil die Nebenbedingungen eliminiert worden sind. Bei Fehlen von
Nebenbedingungen ist
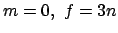 .
.
Aus der Transformation (11.24) folgt für die Variation
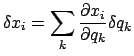 |
(1125) |
und für die Zeitableitung
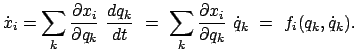 |
(1126) |
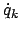 heißen die verallgemeinerten oder
generalisierten Geschwindigkeiten
(z.B. in Kugelkoordinaten
heißen die verallgemeinerten oder
generalisierten Geschwindigkeiten
(z.B. in Kugelkoordinaten  ,
,  ,
,  sind dies
sind dies
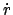 ,
,
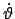 ,
,
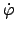 ).
Diese sind im allgemeinen verschieden von den sog. physikalischen
Geschwindigkeitskoordinaten, die in den Gln. (8.67) und (8.67a) angegeben worden
sind. Letztere sind in Kugelkoordinaten
).
Diese sind im allgemeinen verschieden von den sog. physikalischen
Geschwindigkeitskoordinaten, die in den Gln. (8.67) und (8.67a) angegeben worden
sind. Letztere sind in Kugelkoordinaten
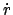 ,
,
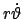 ,
,
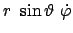 .
.
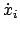 ist nach Gl. (11.26) eine gegebene Funktion der
ist nach Gl. (11.26) eine gegebene Funktion der
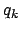 und
und
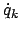 .
Diese kann partiell nach
.
Diese kann partiell nach
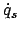 abgeleitet werden
abgeleitet werden
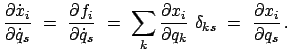 |
(1127) |
Mittels (11.24) und (11.25) werden die verschiedenen Terme der Lagrangeschen
Zentralgleichung (11.23) umgeformt. Der Term auf der rechten Seite wird
T ist die kinetische Energie. Für deren Ausdruck kann man noch eine etwas andere,
sehr zweckmäßige Form angeben. Dazu wird vorausgesetzt, daß es sich nur um
Teilchen der Masse  im dreidimensionalen Raum handelt. Dann ergibt sich
durch Einsetzen von Gl. (11.26) der folgende Ausdruck:
im dreidimensionalen Raum handelt. Dann ergibt sich
durch Einsetzen von Gl. (11.26) der folgende Ausdruck:
Im obigen Ausdruck ist 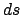 das Bogenelement der krummlinigen Koordinaten
das Bogenelement der krummlinigen Koordinaten
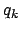 und
und 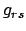 der zugehörige Maßtensor [11.1]. Für die
gängigen Koordinatensysteme findet man diese Ausdrücke fix und fertig berechnet
in entsprechenden Handbüchern [11.2,3].
der zugehörige Maßtensor [11.1]. Für die
gängigen Koordinatensysteme findet man diese Ausdrücke fix und fertig berechnet
in entsprechenden Handbüchern [11.2,3].
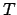 in Gl. (11.30) ist eine Funktion von
in Gl. (11.30) ist eine Funktion von
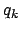 und
und
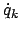 . Daher ergibt sich für die Variation der
kinetischen Energie
. Daher ergibt sich für die Variation der
kinetischen Energie
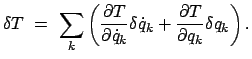 |
(1131) |
Für die Variation der Arbeit ergibt sich mit Gl. (11.25)
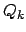 ist die Komponente der generalisierten Kraft in der
ist die Komponente der generalisierten Kraft in der
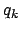 -Richtung. Z.B.
für eine Zentralkraft
-Richtung. Z.B.
für eine Zentralkraft
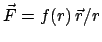 ist in Kugelkoordinaten
ist in Kugelkoordinaten
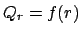 ,
,
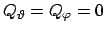 . Läßt man in der
Transformation (11.24) alle Variablen
. Läßt man in der
Transformation (11.24) alle Variablen 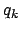 fix, außer einer,
fix, außer einer, 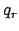 ,
dann beschreibt
eine Raumkurve im
,
dann beschreibt
eine Raumkurve im 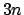 -dimensionalen Raum der
-dimensionalen Raum der 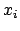 .
.
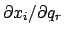 ist der Tangentenvektor an diese Raumkurve.
Das innere Produkt der Kraft mit diesem Tangentenvektor in Gl. (11.32) gibt die
Projektion der Kraft
ist der Tangentenvektor an diese Raumkurve.
Das innere Produkt der Kraft mit diesem Tangentenvektor in Gl. (11.32) gibt die
Projektion der Kraft 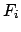 auf diesen ortsabhängigen Tangentenvektor.
auf diesen ortsabhängigen Tangentenvektor.
Einsetzen der Resultate von Gln. (11.25), (11.31)
und (11.32) in die Lagrangesche Zentralgleichung (11.23) gibt:
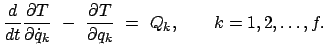 |
(1133) |
Da die Variationen
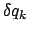 vollständig unabhängig sind, müssen ihre
Koeffizienten verschwinden. Das gibt dann die obige verallgemeinerte
Bewegungsgleichung
(Lagrangesche Gleichung zweiter Art) mit der kinetischen Energie
vollständig unabhängig sind, müssen ihre
Koeffizienten verschwinden. Das gibt dann die obige verallgemeinerte
Bewegungsgleichung
(Lagrangesche Gleichung zweiter Art) mit der kinetischen Energie 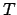 aus Gl. (11.29) bzw. (11.30).
aus Gl. (11.29) bzw. (11.30).
Existiert ein Potential für die Kraft, kann man dieses gemäß der
Transformation (11.24) umrechnen
Dies in Gl. (11.33) eingesetzt, gibt
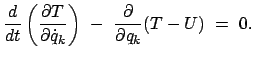 |
(1136) |
Da das Potential nicht geschwindigkeitsabhängig ist, kann man die
Lagrangefunktion (E.: Lagrangian)
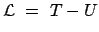 |
(1137) |
definieren und damit der Bewegungsgleichung (11.36) die folgende
endgültige Form der Lagrangeschen Gleichung 2. Art geben
 |
(1138) |
Literaturangaben zu krummlinigen Koordinaten
- 11.1
- W. Papousek: Vektor-, Tensorrechnung II, Kap.VI.
- 11.2
- E. Madelung: Die mathematischen Hilfsmittel des Physikers.
Springer 1964, 1. Teil, 8. Abschnitt
- 11.3
- P. Moon, D.E. Spencer: Field Theory Handbook. Springer 1988.
Existiert für die Kraft 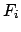 oder für gewisse Teile derselben kein
Potential, muß man Gl. (11.33) heranziehen. Ist
oder für gewisse Teile derselben kein
Potential, muß man Gl. (11.33) heranziehen. Ist 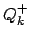 der Anteil der Kraft, für den kein Potential existiert, dann sind
die Bewegungsgleichungen
der Anteil der Kraft, für den kein Potential existiert, dann sind
die Bewegungsgleichungen
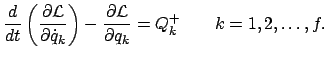 |
(1139) |
Insbesondere existiert kein Potential für geschwindigkeitsabhängige Kräfte
(wie z.B. Reibungskräfte).
Doch gibt es unter den geschwindigkeitsabhängigen Kräften solche, bei denen
die Kraft auf der Geschwindigkeit senkrecht steht (z.B. die Lorentzkraft
![$ e[\vec{v},\vec{B}]$](img3095.gif) auf ein sich mit der Geschwindigkeit
auf ein sich mit der Geschwindigkeit 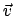 im
Magnetfeld
im
Magnetfeld 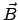 bewegendes geladenes Teilchen) und daher keine Arbeit
leisten kann. Für solche Kräfte
existiert ein verallgemeinertes Potential M, aus dem sich die Kraft
berechnen läßt nach
bewegendes geladenes Teilchen) und daher keine Arbeit
leisten kann. Für solche Kräfte
existiert ein verallgemeinertes Potential M, aus dem sich die Kraft
berechnen läßt nach
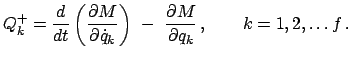 |
(1140) |
Dann gilt wieder die Lagrangesche Gleichung 2. Art, Gl. (11.38), mit der
Lagrangefunktion
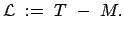 |
(1141) |
Die Bewegung eines Teilchens der Masse  und der Ladung
und der Ladung 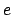 in einem
elektrischen Feld
in einem
elektrischen Feld
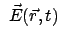 und einem magnetischen Feld
(magnetische Induktion
und einem magnetischen Feld
(magnetische Induktion
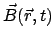 ) ist in MKSA-Einheiten
) ist in MKSA-Einheiten
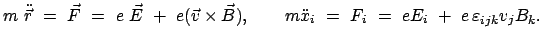 |
(1142) |
Die Lorentzkraft (der zweite Term) ist zwar geschwindigkeitsabhängig, jedoch
ist
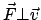 . Es gibt ein verallgemeinertes Potential. Um dieses
angeben zu können, müssen die beiden Felder
. Es gibt ein verallgemeinertes Potential. Um dieses
angeben zu können, müssen die beiden Felder 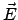 und
und 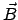 durch das skalare Potential
durch das skalare Potential 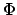 und das Vektorpotential
und das Vektorpotential 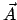 ausgedrückt werden
ausgedrückt werden
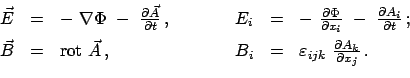 |
(1143) |
Diese Zusammenhänge sowie die Methoden zur Berechnung von
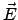 ,
, 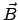 ,
, 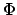 und
und 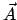 aus den vorgegebenen Ladungen und Strömen werden in der Elektrodynamik
behandelt. Für den gegenwärtigen Gebrauch können wir
aus den vorgegebenen Ladungen und Strömen werden in der Elektrodynamik
behandelt. Für den gegenwärtigen Gebrauch können wir 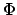 und
und 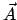 ebenso als
vorgegebene Felder betrachten wie
ebenso als
vorgegebene Felder betrachten wie 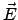 und
und 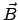 . Die Definitionen
(11.43) werden in den Ausdruck (11.42) für die Lorentzkraft
eingesetzt, die Überschiebung der
. Die Definitionen
(11.43) werden in den Ausdruck (11.42) für die Lorentzkraft
eingesetzt, die Überschiebung der
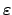 -Tensoren ausgeführt.
-Tensoren ausgeführt.
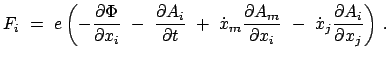 |
(1144) |
Wir definieren das zugehörige verallgemeinerte Potential
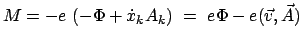 |
(1145) |
und verifizieren durch Ausrechnen die Gültigkeit der Gl. (11.42)
Gemäß Gln. (11.39), (11.40) und der vorhergehenden Gleichung ist daher die
Lagrangefunktion für ein
geladenes Teilchen in einem elektromagnetischen Feld
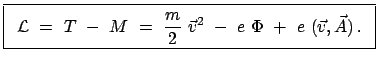 |
(1146) |
Für ein relativistisches Teilchen (Ruhemasse 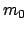 ) gilt statt der
Bewegungsgleichung (11.42) die folgende Bewegungsgleichung (s. §10.6):
) gilt statt der
Bewegungsgleichung (11.42) die folgende Bewegungsgleichung (s. §10.6):
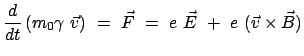 |
(1147) |
mit
Es muß nun in Gl. (11.46) der erste Ausdruck derart abgeändert werden, daß die
gesuchte Lagrangefunktion mittels der Lagrangeschen Gleichung 2. Art, Gl. (11.38),
die obige Bewegungsgleichung (11.47) liefert. Die nachfolgende
Rechnung ergibt als die
Lagrangefunktion für relativistische Bewegung:
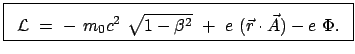 |
(1148) |
Es ist nämlich:
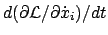 gibt die linke Seite von
Gl. (11.47). Die Punkte deuten die Terme
für die Potentiale an. Für diese läuft die Ableitung ganz wie im
vorhergehenden Paragraphen.
gibt die linke Seite von
Gl. (11.47). Die Punkte deuten die Terme
für die Potentiale an. Für diese läuft die Ableitung ganz wie im
vorhergehenden Paragraphen.
Als Beispiel für die Anwendung der Lagrangeschen Gleichungen zweiter Art
behandeln wir nochmals das sphärische Pendel der Länge R. Wir führen
Kugelkoordinaten
 const.,
const., 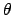 ,
,  ein. Die kinetische und die
potentielle Energie sind:
ein. Die kinetische und die
potentielle Energie sind:
Da die Variable  in der Lgrangefunktion
in der Lgrangefunktion
 nicht explizit vorkommt, ist
die zugehörige Lagrangegleichung 2. Art besonders einfach. Da
nicht explizit vorkommt, ist
die zugehörige Lagrangegleichung 2. Art besonders einfach. Da
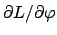 in dieser nicht auftritt, ist
in dieser nicht auftritt, ist
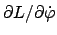 eine Konstante der Bewegung. Vergleich
mit Gl. (6.19) zeigt, daß dies die
eine Konstante der Bewegung. Vergleich
mit Gl. (6.19) zeigt, daß dies die 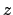 -Komponente des Drehimpulses ist.
-Komponente des Drehimpulses ist.
Die Bewegungsgleichung für 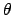 ist:
In dieser wird
ist:
In dieser wird
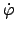 mittels Gl. (11.49) eliminiert und die ganze
Gleichung mit
mittels Gl. (11.49) eliminiert und die ganze
Gleichung mit
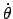 multipliziert. Dann kann man eine Zeitableitung herausziehen:
Diese Bewegungskonstante ist die Gesamtenergie
multipliziert. Dann kann man eine Zeitableitung herausziehen:
Diese Bewegungskonstante ist die Gesamtenergie 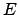 .
.
Diese Gleichung stimmt mit Gl. (6.20(b)) überein. Dort wird auch ihre Lösung
diskutiert.
Das Doppelpendel
Das Doppelpendel ist ein System mit zwei gekoppelten Schwingungsfreiheitsgraden
(s. Abb. 11.4). Es kann als einfaches Modell einer Glocke dienen. 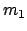 entspricht
dem Glockenkörper,
entspricht
dem Glockenkörper, 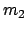 dem Klöppel. Die zweckmäßigsten Koordinaten
sind die
beiden Winkel
dem Klöppel. Die zweckmäßigsten Koordinaten
sind die
beiden Winkel
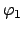 und
und
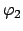 . In ihnen werden die
Kartesischen Koordinaten der
beiden Massenpunkte, danach die kinetische und potentielle Energie und die
Lagrangefunktion ausgedrückt:
. In ihnen werden die
Kartesischen Koordinaten der
beiden Massenpunkte, danach die kinetische und potentielle Energie und die
Lagrangefunktion ausgedrückt:
Die Bewegungsgleichungen sind wieder die Lagrangeschen Gleichungen 2. Art,
Gln. (11.38):
Dies ist ein System nichtlinearer gekoppelter Differentialgleichungen.
Damit man analytisch weiterrechnen kann, beschränkt man sich auf
die Näherung für kleine Schwingungen, in der alle in den
Winkeln nichtlinearen Terme vernachlässigt werden.
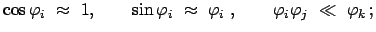 |
(1155) |
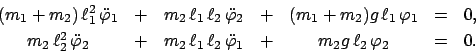 |
(1156) |
Es wird nun aus der ersten (zweiten) der obigen Gleichungen
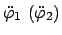 berechnet und in die
zweite (erste) Gleichung eingesetzt. Dies gibt dann folgendes neue System:
berechnet und in die
zweite (erste) Gleichung eingesetzt. Dies gibt dann folgendes neue System:
Das Problem wird nochmals vereinfacht durch folgende weitere Spezialisierungen:
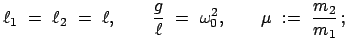 |
(1157) |
Die linke Seite jeder der obigen Gleichungen erfasst die Bewegung
des einzelnen Pendels, die rechte Seite gibt die Kopplung an das
jeweils andere. Ist die Masse 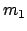 viel schwerer als
viel schwerer als 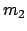 (bei einer Glocke ist die Masse des Klöppels klein gegen die des Körpers),
also
(bei einer Glocke ist die Masse des Klöppels klein gegen die des Körpers),
also 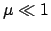 , dann ist die Wirkung von
, dann ist die Wirkung von 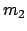 auf
auf 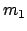 viel
geringer als die von
viel
geringer als die von 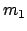 auf
auf 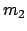 . Dies zeigt sich in den
obigen Gleichungen: Auf der rechten Seite der ersten steht der Faktor
. Dies zeigt sich in den
obigen Gleichungen: Auf der rechten Seite der ersten steht der Faktor 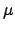 ,
der klein ist im Vergleich mit dem Faktor
,
der klein ist im Vergleich mit dem Faktor
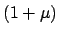 auf der rechten
Seite der zweiten Gleichung.
auf der rechten
Seite der zweiten Gleichung.
Dieses System gekoppelter linearer Schwingungsgleichungen wird durch Exponentialansätze
gelöst
Das lineare homogene Gleichungssystem in den 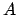 ,
, 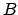 , das durch Einsetzen der
Exponentialansätze in die vorhergehenden Differentialgleichungen erhalten
worden ist, hat nur dann nichttriviale Lösungen für
, das durch Einsetzen der
Exponentialansätze in die vorhergehenden Differentialgleichungen erhalten
worden ist, hat nur dann nichttriviale Lösungen für 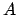 ,
, 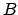 , wenn die
Determinante
verschwindet. Dies gibt eine biquadratische Gleichung für die Eigenwerte
, wenn die
Determinante
verschwindet. Dies gibt eine biquadratische Gleichung für die Eigenwerte
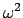 :
:
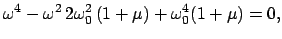 |
(1160) |
mit folgenden Wurzeln
Zu jeder dieser Wurzeln gehört dann ein bestimmtes Verhältnis der
beiden Amplituden  und
und  :
Die Eigenwerte
:
Die Eigenwerte
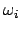 geben die Eigenfrequenzen des Systems, die
zugehörigen
Amplitudenverhältnisse
geben die Eigenfrequenzen des Systems, die
zugehörigen
Amplitudenverhältnisse 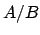 folgen aus der letzten Gleichung durch Einsetzen
der
folgen aus der letzten Gleichung durch Einsetzen
der
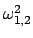 .
.
Diese Lösung wird noch weiter vereinfacht durch die Annahme, daß 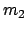 leicht gegenüber
leicht gegenüber 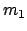 ist.
ist.
Nach den vorgehenden Annahmen haben beide Pendel gleiche Länge, daher gleiche Frequenz,
nämlich 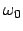 . Die Wechselwirkung erhöht eine der beiden Freqenzen und
erniedrigt die andere (s. Abb. 11.5).
. Die Wechselwirkung erhöht eine der beiden Freqenzen und
erniedrigt die andere (s. Abb. 11.5).
Abbildung:
Die Abhängigkeit der Eigenfrequenzen 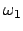 und
und 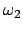 von der Kopplungsstärke
von der Kopplungsstärke 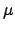 .Notebook:
K11DoppelPend.nb.
.Notebook:
K11DoppelPend.nb.
|
|
Abbildung 11.6:
Schwingungen der beiden Teile eines Doppelpendels bei kleinen
Amplituden. Notebook: K11DoppelPend.nb.
|
|
Aus den rechten Seiten der Gln. (11.58) und
(11.59) ersieht man, daß das erste Pendel
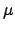 -mal schwächer an das zweite gekoppelt ist als umgekehrt. Darum
ist auch die
Amplitude
-mal schwächer an das zweite gekoppelt ist als umgekehrt. Darum
ist auch die
Amplitude
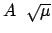 -mal kleiner als
-mal kleiner als 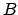 . Statt der
imaginären Exponentialfunktionen benützen wir nun
trigonometrische Funktionen:
. Statt der
imaginären Exponentialfunktionen benützen wir nun
trigonometrische Funktionen:
Als Anfangsbedingung wählen wir einen kurzen Stoss gegen den Glockenkörper,
während dieser und der Klöppel in der Ruhelage herabhängen.
Damit erhält dieser eine Anfangswinkelgeschwindigkeit
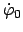 .
.
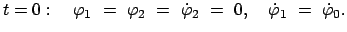 |
(1161) |
Dies gibt folgende Werte der Integrationskonstanten:
Damit nimmt die Lösung folgende Gestalt an:
Dabei wurden folgende Relationen benützt:
Die erste trigonometrische Funktion (Frequenz
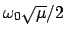 ) ist
langsam veränderlich gegenüber der zweiten; sie stellt eine Einhüllende
(Amplitudenmodulation)
der schnellen Oszillationen (Frequenz
) ist
langsam veränderlich gegenüber der zweiten; sie stellt eine Einhüllende
(Amplitudenmodulation)
der schnellen Oszillationen (Frequenz
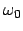 ) dar. Das eine Pendel kommt
zur Ruhe, wenn das andere maximale Amplitude hat. Die Energie wandert
zwischen den beiden Pendeln hin und her. Die Amplitude des ersten Pendels ist
) dar. Das eine Pendel kommt
zur Ruhe, wenn das andere maximale Amplitude hat. Die Energie wandert
zwischen den beiden Pendeln hin und her. Die Amplitude des ersten Pendels ist
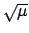 -fach kleiner als die des zweiten (s. Abb. 11.6).
-fach kleiner als die des zweiten (s. Abb. 11.6).
Aus den Gleichungen (11.62) kann man auch die Poincaré Abbildung finden.
Im vierdimensionalen Phasenraum entsprechen die Ebenen
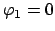
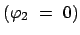 den Argumenten
den Argumenten
![$ \omega_{0} t_n = \pi n [\pi (n + 1/2)] $](img3190.gif) mit
mit
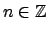 .
Zusammen mit der Zeitableitung von (11.62) erhält man zu diesen
Werten
.
Zusammen mit der Zeitableitung von (11.62) erhält man zu diesen
Werten
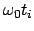 folgende Punkte in der
folgende Punkte in der
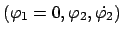 bzw.
bzw.
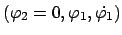 -Ebene:
-Ebene:
Für stetiges 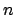 gibt jedes der obigen Funktionenpaare die Parameterdarstellung
einer Ellipse, deren Halbachsen das Verhältnis
gibt jedes der obigen Funktionenpaare die Parameterdarstellung
einer Ellipse, deren Halbachsen das Verhältnis
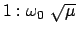 (oder umgekehrt) haben; für diskrete
(oder umgekehrt) haben; für diskrete 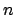 erhält man Punkte auf diesen.
erhält man Punkte auf diesen.
Abbildung:
Schwingungen der beiden Teile eines Doppelpendels bei grossen Amplituden.
Links: Die Winkel
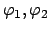 . Rechts der Poincaréschnitt für
. Rechts der Poincaréschnitt für
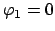 . Notebook: K11DoppelPend.nb.
. Notebook: K11DoppelPend.nb.
![\includegraphics[width=16cm]{K11dp5}](img3200.gif) |
Die obigen Abbildungen geben ein sehr einfaches, übersichtliches Bild für das
Verhalten des Doppelpendels. Diese einfache Form der Schwingung resultiert
aus den Vereinfachungen. Im allgemeinen Fall kann die Bewegung sehr
unübersichtlich, eben chaotisch sein; dann läßt sich nicht mehr
aus dem Verlauf der Schwingung während eines gewissen Zeitintervalls
der weitere Verlauf voraussagen.
Abb. 11.7 zeigt den Verlauf einer Schwingung eines Doppelpendels für grosse
Schwingungsamplituden. Die Kurven wurden durch numerische Integration der
nichtlinearen Bewegungsgleichungen (11.53) und (11.54) bestimmt.
Aus dem unregelmäßigen Verlauf läßt sich nicht vorhersehen, wie die
Bewegung weitergehen wird.
(Deterministisches Chaos. Die Termini: ''Deterministisch'' oder ''kausal''
besagen hier: Die Bewegungsgleichungen bestimmen eindeutig den weiteren Verlauf des
Vorganges). Weitere Beispiele chaotischer Bewegungen finden sich im Notebook:
K11DoppelPend.nb.
Die Lagrangefunktion für ein System von gekoppelten linearenSchwingern lautet:
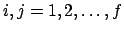 . Es gilt das Summationsübereinkommen.
Die Massenmatrix M =
. Es gilt das Summationsübereinkommen.
Die Massenmatrix M = 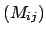 und Potentialmatrix P =
und Potentialmatrix P = 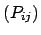 sind reelle, symmetrische Matrizen. Die
Massenmatrix ist zusätzlich positiv definit, d.h. sie hat nur positive Eigenwerte
sind reelle, symmetrische Matrizen. Die
Massenmatrix ist zusätzlich positiv definit, d.h. sie hat nur positive Eigenwerte 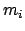 ; deswegen
gilt:
solange nicht alle
; deswegen
gilt:
solange nicht alle
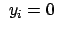 sind. Die Bewegungsgleichungen sind die Lagrangeschen Gleichungen
2. Art:
sind. Die Bewegungsgleichungen sind die Lagrangeschen Gleichungen
2. Art:
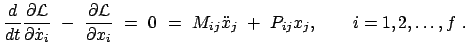 |
(1165) |
Sie sind ein System von gekoppelten Schwingungsgleichungen. Dieses läßt sich entkoppeln
durch Einführung von Normalkoordinaten. Die zugehörigen Normalschwingungen sind die
Eigenschwingungen des Systems. Das Verfahren ist eine Verallgemeinerung der Methode der
Hauptachentransformation einer Matrix.
Durch den üblichen Lösungsansatz mit einer 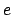 -Potenz wird das obige System
(11.65) in eine rein
algebraische Gleichung transformiert:
-Potenz wird das obige System
(11.65) in eine rein
algebraische Gleichung transformiert:
Das ist ein System von 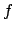 linearen Gleichungen für die
linearen Gleichungen für die 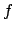 Unbekannten
Unbekannten 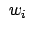 .
Die Koeffizientenmatrix hat
.
Die Koeffizientenmatrix hat 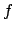 positive Eigenwerte
positive Eigenwerte
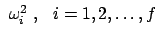 .
Diese berechnet man aus der charakteristischen Gleichung:
.
Diese berechnet man aus der charakteristischen Gleichung:
Die Eigenwerte liefern die Eigenfrequenzen 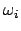 und die zugehörigen Eigenvektoren
und die zugehörigen Eigenvektoren
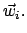 Diese können reell gewählt werden. Diese sind dann die nichttrivialen Lösugen des obigen
linearen Gleichungssystems (11.66).
Diese können reell gewählt werden. Diese sind dann die nichttrivialen Lösugen des obigen
linearen Gleichungssystems (11.66).
Diese Eigenvektoren müssen eine verallgemeinerte Orthonormalitätsrelation erfüllen,
in der die Massenmatrix M die Rolle eines Maßtensors spielt:
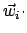 M M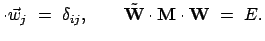 |
(1169) |
W =
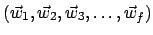 ist eine
ist eine
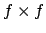 Matrix,
deren Spalten aus den
Matrix,
deren Spalten aus den 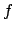 Eigenvektoren
Eigenvektoren 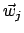 bestehen.
bestehen.
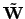 ist die
transponierte Matrix. Es gilt dann weiter:
ist die
transponierte Matrix. Es gilt dann weiter:
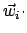 P P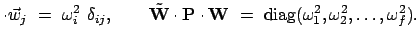 |
(1170) |
Damit sind die Werkzeuge bereitgestellt, mit deren Hilfe die Langrangefunktion auf
Normalform gebracht werden kann.
Die 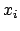 aus Gln. (11.64) und (11.65) werden nun zu einem Vektor
zusammengefasst und dieser wird nach den Eigenvektoren
aus Gln. (11.64) und (11.65) werden nun zu einem Vektor
zusammengefasst und dieser wird nach den Eigenvektoren 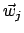 entwickelt:
entwickelt:
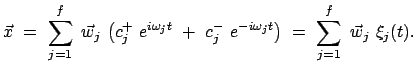 |
(1171) |
Die Koeffizienten
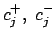 können komplex sein. Doch die obige Lösung
muß reell sein. Daher muß gelten:
Damit kann man den obigen Lösungsvektor folgendermaßen schreiben:
können komplex sein. Doch die obige Lösung
muß reell sein. Daher muß gelten:
Damit kann man den obigen Lösungsvektor folgendermaßen schreiben:
Dann kann man die kinetische, die potentielle Energie und die Lagrangefunktion
folgendermaßen schreiben:
Die Bewegungsgleichungen sind wieder die Lagrangeschen Gleichungen 2. Art. Diese
sind jetzt entkoppelt.
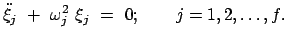 |
(1176) |
Die Anfangsbedingungen, die für die 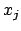 vorgeschrieben waren, müssen ebenfalls
umgerechnet werden:
vorgeschrieben waren, müssen ebenfalls
umgerechnet werden:
Als ein Beispiel werden die Normalschwingungen des Doppelpendels (§11.5.5) berechnet.
In Gln. (11.56) wird
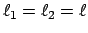 gesetzt und folgende Abkürzungen eingeführt:
gesetzt und folgende Abkürzungen eingeführt:
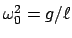 und
und
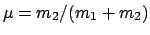 . Die resultierenden Bewegungsgleichungen sind:
. Die resultierenden Bewegungsgleichungen sind:
Die zugehörige Lagrangefunktion ist durch Gl. (11.64) gegeben mit den folgenden Ausdrücken
für die Massen- und Potentialmatrizen:
M![$\displaystyle = \left( \begin{array}{cc} 1/\mu & 1 [2mm] 1 & 1 \end{array} \right) ,$](img3257.gif) P
P![$\displaystyle = \left( \begin{array}{cc} \omega_0^2 / \mu & 0 [2mm] 0 & \omega_0^2 \end{array} \right)
$](img3258.gif)
Abbildung 11.8:
Zeitverhalten der beiden Normalschwingungen des mathematischen Pendels.
|
|
Damit bekommt man aus Gl. (11.67) folgende Eigenwerte:
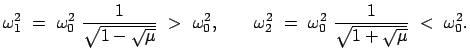 |
(1178) |
Die Eigenvektoren, die gemäß Gl. (11.69) orthonormiert sind, lauten:
Als Lösung der Lagrangeschen Gleichungen (11.76) können wir hier annehmen:
Dann sind die beiden Normalschwingungen gegeben durch:
Diese beiden Eigenschwingungen sind in Abb. 11.8 und Abb. 11.9 gezeichnet.
Bei der Normalschwingung
mit der höheren Frequenz, 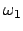 , bewegen sich die beiden Pendel in entgegengesetzter
Richtung; bei der mit der niederen Frequenz,
, bewegen sich die beiden Pendel in entgegengesetzter
Richtung; bei der mit der niederen Frequenz, 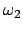 , bewegen sie sich gleichsinnig.
, bewegen sie sich gleichsinnig.
Abbildung 11.9:
Bewegungsrichtung der beiden Pendel bei den jeweiligen Normalschwingungen.
|
|
Auch die spezielle Lösung, die im vorhergehenden Paragraphen zu den Anfangsbedingungen
(11.61) aufgestellt wurde, kann durch die beiden Normalschwingungen ausgedrückt werden.
Setzt man diese Anfangsbedingungen in Gln. (11.77) ein, so ergibt sich:
Führt man diese Anfangsbedingungen in die allgemeine Lösung der Lagrangeschen
Gleichungen
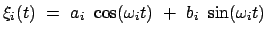 ein, so ergibt sich:
Entwickelt man die Kreisfrequenzen
ein, so ergibt sich:
Entwickelt man die Kreisfrequenzen 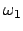 und
und 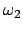 , Gl. (11.78)
nach dem kleinen Paramter
, Gl. (11.78)
nach dem kleinen Paramter
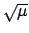 bis zur ersten Ordnung, so erhält man:
Die beiden vorhergehenden Resultate werden in die Gl. (11.72) eingesetzt. Doch werden in den
trigonometrischen Funktionen die ursprünglichen Kreisfrequenzen
bis zur ersten Ordnung, so erhält man:
Die beiden vorhergehenden Resultate werden in die Gl. (11.72) eingesetzt. Doch werden in den
trigonometrischen Funktionen die ursprünglichen Kreisfrequenzen 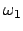 und
und 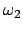 beibehalten. Dann findet man:
beibehalten. Dann findet man:
Im Nenner wird 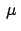 gegen 4 vernachläßigt, im Zähler der Term prorportional
zu
gegen 4 vernachläßigt, im Zähler der Term prorportional
zu
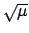 . Dieses Resultat stimmt mit der ersten Zeile von Gl. (11.62) überein.
. Dieses Resultat stimmt mit der ersten Zeile von Gl. (11.62) überein.
Auch dieses Prinzip wird aus der Lagrangeschen Zentrlgleichung (11.23) abgeleitet,
nachdem Gl. (11.25) eingesetzt worden ist:
Für Kräfte mit Potential kann gemäß Gln. (11.32) und (11.35)
die Variation der Arbeit
in der obigen Gleichung durch die des Potentials ersetzt werden
Im Gegensatz zur Betrachtungsweise im Kleinen, die bisher bei der Ableitung der
verschiedenen Prinzipe angewendet worden ist, soll nun die Bahn als Ganzes
während eines endlichen Zeitintervalles untersucht werden. In der Zeit von
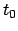 bis
bis 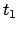 ändern sich die Koordinaten des Systems von
ändern sich die Koordinaten des Systems von
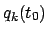 zu
zu
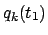 .
Wir vergleichen nun diese wahre Bahn (die vom System tatsächlich durchlaufen
wird) mit virtuellen Bahnen in der Nähe der wahren Bahn (vgl. Abb. A.1). Dabei
sollen auch die Vergleichsbahnen durch den gleichen Anfangs- und Endpunkt gehen, d.h.
.
Wir vergleichen nun diese wahre Bahn (die vom System tatsächlich durchlaufen
wird) mit virtuellen Bahnen in der Nähe der wahren Bahn (vgl. Abb. A.1). Dabei
sollen auch die Vergleichsbahnen durch den gleichen Anfangs- und Endpunkt gehen, d.h.
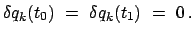 |
(1180) |
Da das Intervall, das bisher betrachtet wird, nicht infinitesimal ist, muß
über Gl. (11.79) von 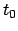 bis
bis 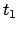 integriert werden. Dabei darf das
Variationszeichen vor das Integral gezogen werden. Danach ist der Integrand
die Lagrangefunktion
integriert werden. Dabei darf das
Variationszeichen vor das Integral gezogen werden. Danach ist der Integrand
die Lagrangefunktion
 , Gl. (11.37).
, Gl. (11.37).
Die rechte Seite der obigen Gleichung ist eine totale Ableitung, daher kann das
Integral sofort ausgeführt werden; wegen Bedingung (11.80) verschwindet es.
Daher folgt aus der obigen Gleichung
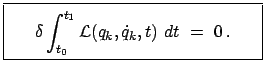 |
(1181) |
Dies ist das Hamiltonsche Prinzip. Die Bewegung des Systems zwischen
den Zeitpunkten 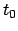 und
und 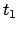 ist derart, daß das folgende Linienintegral
ist derart, daß das folgende Linienintegral
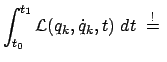
Extr.
für die tatsächlich durchlaufene Bahn ein Extremum (oder stationär) ist.
Die Eulerschen Differentialgleichungen zu dem Variationsprinzip (11.81) (vgl.
Gl. (A.14) sind die Lagrangeschen Gleichungen 2. Art (s. Gl. (11.38))
Für Untersuchungen allgemeiner Art ist aber das Variationsprinzip (11.81)
günstiger als die eben angegebenen Differentialgleichungen.
Wir werden es im nächsten Kapitel
benützen, um weitere Formen von Bewegungsgleichungen und Methoden zu deren
Integration abzuleiten.
Die Lagrangefunktion für ein System von 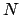 Massenpunkten lautet:
Massenpunkten lautet:
mit
Die Teilchen und Koordinatenindices werden wieder fortlaufend numeriert,
vgl. (11.10).
Damit lauten dann die Lagrangeschen Gleichungen 2. Art:
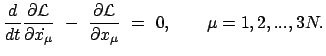 |
(1183) |
Das Hamiltonsche Prinzip ermöglicht es, den Zusammenhang zwischen den Symmetrien eines
physikalischen Problems, die in der Lagrangefunktion ihren Niederschlag finden, und
zugeordneten Erhaltungsgrößen zu zeigen. Jeder Symmetrie entsprechen Transformationen,
die die Lagrangefunktion (oder zumindest das Hamiltonsche Prinzip) unverändert lassen.
Dabei genügt es bereits von diesen Symmetrieoperationen die infinitesimalen einzusetzen,
z.B. genügt es, bei Drehungen solche um ganz kleine Winkel zu verwenden. Dies vereinfacht
die Rechnung beträchtlich.
Wir werden zeigen, daß bei einem nicht zeitabhängigen Problem im homogenen Raum Invarianz
gegen mindestens 10 Symmetrieoperationen gegeben ist und damit jeweils eine Erhaltungsgrösse
verknüpft ist; nämlich:
Operation Erhaltungsgröße Anzahl
Zeitverschiebung Energie 1
Drehungen Drehimpuls 3
Translationen Impuls 3
Boosts Anfangsschwerpunkt 3
Die Lagrangefunktion hängt nicht explizit von der Zeit  ab:
ab:
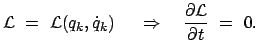 |
(1184) |
Damit ist das Hamiltonsche Prinzip
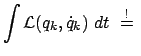 Extr Extr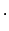 |
(1185) |
invariant gegen eine Verschiebung der Zeit
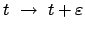 . Im Anhang zu diesem
Kapitel (Gl. (A.9)) wird gezeigt, daß dann das Jacobiintegral des
Variationsproblems erhalten ist:
. Im Anhang zu diesem
Kapitel (Gl. (A.9)) wird gezeigt, daß dann das Jacobiintegral des
Variationsproblems erhalten ist:
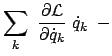 |
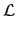 |
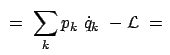 const. const. |
(1186) |
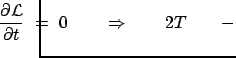 |
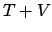 |
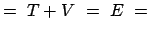 const. const. |
(1187) |
Vergleiche hiezu auch die Gln. (12.16) und
(12.17). Jetzt wird gezeigt, daß die Invarianz gegen
Zeitverschiebungen impliziert, daß die partielle Ableitung der Lagrangefunktion nach der
Zeit Null ist. Dazu wird eine Taylorreihenentwicklung nach
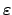 herangezogen.
herangezogen.
Vergleich der oberen mit der unteren Zeile ergibt dann:
Infinitesimale Koordinatentransformationen werden in folgender Form geschrieben:
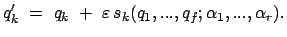 |
(1189) |
Darin geben die Funktionen 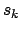 die Transformationen; diese wirken auf die Koordinaten
die Transformationen; diese wirken auf die Koordinaten
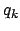 und führen diese in die
und führen diese in die 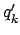 über; die Paramter
über; die Paramter 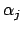 kennzeichnen die
Transformation, z.B. bei einer Drehung im dreidimensionalen Raum sind dies die drei Drehwinkel.
kennzeichnen die
Transformation, z.B. bei einer Drehung im dreidimensionalen Raum sind dies die drei Drehwinkel.
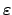 ist so klein, daß alle seine höheren Potenzen vernachläßigt werden können;
dies charakterisiert infinitesimale Transformationen.
So haben wir bei Translationen:
ist so klein, daß alle seine höheren Potenzen vernachläßigt werden können;
dies charakterisiert infinitesimale Transformationen.
So haben wir bei Translationen:
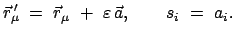 |
(1190) |
Bei den Drehungen gehen wir von den endlichen Drehungen auf die infinitesimalen über.
Dazu werden die ersteren durch den Drehtensor ausgedrückt:
Beim Übergang zur letzten Zeile wurde angenommen, daß der Drehwinkel
 klein ist,
deswegen
klein ist,
deswegen
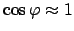 und
und
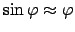 gesetzt
werden können.
Dieser kleine Drehwinkel wird mit den Komponenten der Drehachse
multipliziert; dies gibt den Drehvektor:
gesetzt
werden können.
Dieser kleine Drehwinkel wird mit den Komponenten der Drehachse
multipliziert; dies gibt den Drehvektor:
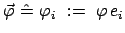 . Damit können die Drehungen
zu infinitesimalen umgeschrieben werden:
. Damit können die Drehungen
zu infinitesimalen umgeschrieben werden:
In der ersten Zeile wurde der Teilchenindex 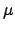 nicht angeschrieben. In der letzten Zeile
wurde der infinitesimale Charakter der Drehung durch das Einfügen des
nicht angeschrieben. In der letzten Zeile
wurde der infinitesimale Charakter der Drehung durch das Einfügen des
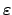 hervorgehoben.
hervorgehoben.
Die Geschwindigkeitstransformationen = Boosts tragen dem
Relativitätsprinzip Rechnung, nämlich,
daß die Physik in allen Inertialsystemen gleich abläuft.
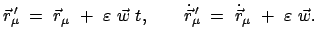 |
(1192) |
Nun wird ein allgemeiner Ausdruck für die Erhaltungsgrößen abgeleitet.
Die infinitesimale Transformation (11.89) wird in die Lagrangefunktion eingesetzt und der
Ausdruck nach
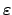 bis zur ersten Ordnung entwickelt:
bis zur ersten Ordnung entwickelt:
Daraus folgt wieder:
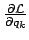 wird mittels der Lagrangeschen
Gl. 2. Art (11.38) durch
wird mittels der Lagrangeschen
Gl. 2. Art (11.38) durch
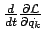 ersetzt. Dann
kann man die Zeitableitung herausziehen und
bekommt:
ersetzt. Dann
kann man die Zeitableitung herausziehen und
bekommt:
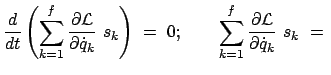 const. const. |
(1195) |
Dies gibt nun das Theorem von E. Noether:
Aus der Invarianz der Lagrangefunktion unter einer  -parametrigen
infinitesimalen Transformation,
eq. (11.89), folgt die Existenz von
-parametrigen
infinitesimalen Transformation,
eq. (11.89), folgt die Existenz von  Konstanten der Bewegung wie
sie in der vorstehenden
Gleichung angegeben worden sind für die Lagrangefunktion:
Konstanten der Bewegung wie
sie in der vorstehenden
Gleichung angegeben worden sind für die Lagrangefunktion:
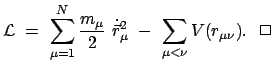 |
(1196) |
Aus der Invarianz gegen Translationen
im Raum folgt die Erhaltung des Gesamtimpulses. Denn die Erhaltungsgröß
e, Gl. (11.95)
wird dann für die Lagrangefunktion (11.96):
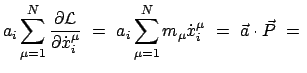 const. const.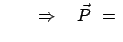 const. const. |
(1198) |
Da 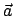 vollständig willkürlich ist, folgt aus der Konstanz des Skalarprodukts
vollständig willkürlich ist, folgt aus der Konstanz des Skalarprodukts
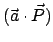 die Konstanz jeder einzelnen Komponents des Gesamtimpulses.
die Konstanz jeder einzelnen Komponents des Gesamtimpulses.
Aus den infinitesimalen Drehungen (11.91)
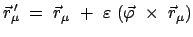 |
(1199) |
ergibt sich für die Invariante (11.95)
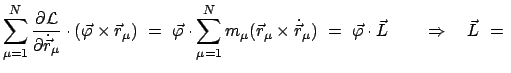 const. const. |
(11100) |
Aus der Invarianz der Lagrangefunktion (11.96) gegenüber der Wahl
der Geschwindigkeit des Inertialsystems folgt die Erhaltung des
Anfangsschwerpunkts
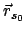 (vgl. Gln. (7.9) und
(7.10)).
(vgl. Gln. (7.9) und
(7.10)).
Zum Beweis dieses Zusammenhangs muß eine Verallgemeinerung des
Noetherschen Theorems abgeleitet werden. Wir wählen für die Invarianz
der Lagrangefunktion gegenüber den
Symmetrie-Transformationen (11.89) die folgende allgemeinere Bedingung:
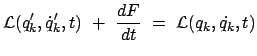 |
(11101) |
mit einer willkürlichen Funktion 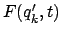 . Für beide Lagrangefunktionen liefert das
Hamiltonsche Prinzip die gleiche Eulersche Gleichung, also die gleiche Lagrangesche Gleichung 2. Art.
Denn bildet man die Zeitableitung
dieser Funktion und leitet diese nach
. Für beide Lagrangefunktionen liefert das
Hamiltonsche Prinzip die gleiche Eulersche Gleichung, also die gleiche Lagrangesche Gleichung 2. Art.
Denn bildet man die Zeitableitung
dieser Funktion und leitet diese nach
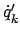 ab, so ergibt sich:
ab, so ergibt sich:
und damit
Für
 ist die transformierte Lagrangefunktion gleich
der ursprünglichen,
daher muß die Funktion
ist die transformierte Lagrangefunktion gleich
der ursprünglichen,
daher muß die Funktion 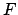 mindestens proportional zu
mindestens proportional zu
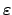 sein.
Die Reihenentwicklung
der Lagrangefunktion nach
sein.
Die Reihenentwicklung
der Lagrangefunktion nach
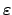 enthält dann einen zusätzlichen Term.
enthält dann einen zusätzlichen Term.
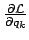 wird mittels der Lagrangeschen Gl. 2. Art durch
wird mittels der Lagrangeschen Gl. 2. Art durch
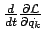 ersetzt. Dann
kann man die Zeitableitung herausziehen und bekommt:
ersetzt. Dann
kann man die Zeitableitung herausziehen und bekommt:
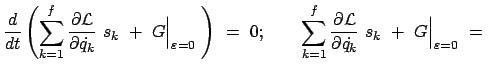 const. const. |
(11102) |
Die Geschwindigkeitstransformationen (11.92)
werden nun in die Lagrangefunktion (11.96) eingesetzt. Dies gibt
Der 2. Term in der letzten Zeile kann unter Benutzung der Definition des Schwerpunkts umgeschrieben
werden zu:
Damit ergibt sich aus dem obigen Formelblock:
mit
Daraus ergibt sich für die Invariante:
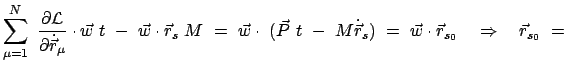 const. const. |
(11103) |
Wegen der Willkürlichkeit von  ergibt sich daraus wieder die Konstanz des
Anfangsschwerpunkts.
ergibt sich daraus wieder die Konstanz des
Anfangsschwerpunkts.
In der folgenden Tabelle sind die Invarianzoperationen, die damit
zusammenhängenden Eigenschaften
des Systems und die Erhaltungsgrößen aufgelistet.
| Operation |
Eigenschaft |
Erhaltungsgröße |
| Translation |
Homogenität des Raumes |
Gesamtimpuls  |
| Drehung |
Isotropie des Raumes |
Gesamtdrehimpuls 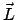 |
| Zeitverschiebung |
Homogenität der Zeit |
Gesamtenergie 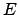 |
| Boost |
Gleichwertigkeit der Inertialsysteme |
Anfangsschwerpunkt
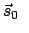 |
Christian Sommer
2003-01-27
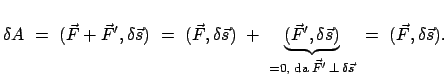
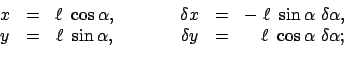
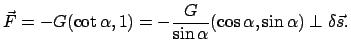
![]() Massenpunkten gelten die
Bewegungsgleichungen
Massenpunkten gelten die
Bewegungsgleichungen
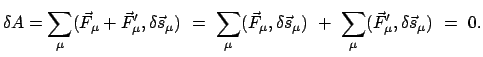
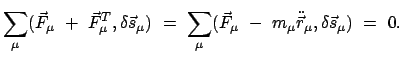

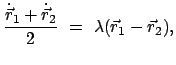
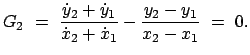
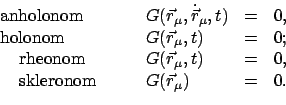
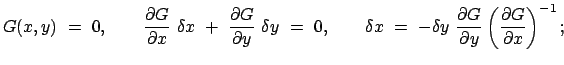
![$\displaystyle \left [ -(F_{x} - m \ddot{x}) \frac{\partial G}{\partial y} \l...
...partial x}\right)^{-1} + (F_{y} - m \ddot{y}) \right ] \delta y = 0.
$](img3013.gif)
![]() multipliziert,
über
multipliziert,
über ![]() summiert und dann zu (11.12) addiert:
summiert und dann zu (11.12) addiert:
![$\displaystyle \sum_{i=1}^{3n} \left[ F_{i} - m_{i} \ddot{x}_{i} + \sum_{\mu...
...bda_{\mu} \frac{\partial G_{\mu}}{\partial x_{i}} \right] \delta x_{i} = 0.$](img3015.gif)
![$\displaystyle \sum_{i=1}^{3n} \Big[ F_{i} - m_{i} \ddot{x}_{i} \Big] \delta x_{i} = 0
$](img3022.gif)
![]() , Gl. (11.18). - Die Gln. (11.18)
und (11.21) gelten nicht bei
den sogenannten ''Quasikoordinaten''; letztere werden über die
Geschwindigkeiten oder Differentiale definiert:
, Gl. (11.18). - Die Gln. (11.18)
und (11.21) gelten nicht bei
den sogenannten ''Quasikoordinaten''; letztere werden über die
Geschwindigkeiten oder Differentiale definiert:
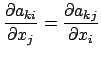
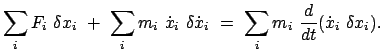
![]() durch die
Transformationen
durch die
Transformationen
![]() ist nach Gl. (11.26) eine gegebene Funktion der
ist nach Gl. (11.26) eine gegebene Funktion der
![]() und
und
![]() .
Diese kann partiell nach
.
Diese kann partiell nach
![]() abgeleitet werden
abgeleitet werden
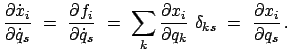
![]() in Gl. (11.30) ist eine Funktion von
in Gl. (11.30) ist eine Funktion von
![]() und
und
![]() . Daher ergibt sich für die Variation der
kinetischen Energie
. Daher ergibt sich für die Variation der
kinetischen Energie
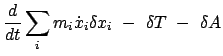
![$\displaystyle \sum_{k} \left[ \frac{d}{dt}
\left( \frac{\partial T}{\partial \d...
... \
\frac{\partial T}{\partial q_{k}} \delta q_{k} - Q_{k} \delta q_{k} \right]$](img3083.gif)
![$\displaystyle \sum_{k} \left[ \frac{d}{dt}
\left( \frac{\partial T}{\partial \d...
...ght) - \
\frac{\partial T}{\partial q_{k}} - Q_{k} \right] \delta q_{k} ;$](img3084.gif)
![]() vollständig unabhängig sind, müssen ihre
Koeffizienten verschwinden. Das gibt dann die obige verallgemeinerte
Bewegungsgleichung
(Lagrangesche Gleichung zweiter Art) mit der kinetischen Energie
vollständig unabhängig sind, müssen ihre
Koeffizienten verschwinden. Das gibt dann die obige verallgemeinerte
Bewegungsgleichung
(Lagrangesche Gleichung zweiter Art) mit der kinetischen Energie ![]() aus Gl. (11.29) bzw. (11.30).
aus Gl. (11.29) bzw. (11.30).
![]() oder für gewisse Teile derselben kein
Potential, muß man Gl. (11.33) heranziehen. Ist
oder für gewisse Teile derselben kein
Potential, muß man Gl. (11.33) heranziehen. Ist ![]() der Anteil der Kraft, für den kein Potential existiert, dann sind
die Bewegungsgleichungen
der Anteil der Kraft, für den kein Potential existiert, dann sind
die Bewegungsgleichungen
![]() auf ein sich mit der Geschwindigkeit
auf ein sich mit der Geschwindigkeit ![]() im
Magnetfeld
im
Magnetfeld ![]() bewegendes geladenes Teilchen) und daher keine Arbeit
leisten kann. Für solche Kräfte
existiert ein verallgemeinertes Potential M, aus dem sich die Kraft
berechnen läßt nach
bewegendes geladenes Teilchen) und daher keine Arbeit
leisten kann. Für solche Kräfte
existiert ein verallgemeinertes Potential M, aus dem sich die Kraft
berechnen läßt nach
![]() und der Ladung
und der Ladung ![]() in einem
elektrischen Feld
in einem
elektrischen Feld
![]() und einem magnetischen Feld
(magnetische Induktion
und einem magnetischen Feld
(magnetische Induktion
![]() ) ist in MKSA-Einheiten
) ist in MKSA-Einheiten
![]() ,
, ![]() ,
, ![]() und
und ![]() aus den vorgegebenen Ladungen und Strömen werden in der Elektrodynamik
behandelt. Für den gegenwärtigen Gebrauch können wir
aus den vorgegebenen Ladungen und Strömen werden in der Elektrodynamik
behandelt. Für den gegenwärtigen Gebrauch können wir ![]() und
und ![]() ebenso als
vorgegebene Felder betrachten wie
ebenso als
vorgegebene Felder betrachten wie ![]() und
und ![]() . Die Definitionen
(11.43) werden in den Ausdruck (11.42) für die Lorentzkraft
eingesetzt, die Überschiebung der
. Die Definitionen
(11.43) werden in den Ausdruck (11.42) für die Lorentzkraft
eingesetzt, die Überschiebung der
![]() -Tensoren ausgeführt.
-Tensoren ausgeführt.
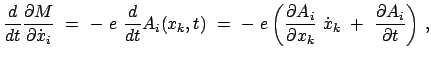
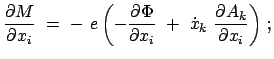
![$\displaystyle \frac{d}{dt} \left( \frac{\partial M}{\partial \dot{x}_{i}} \righ...
... \dot{x}_{k} \frac{\partial A_{i}}{\partial x_{k}} \right] = F_{i} .
$](img3111.gif)
![]() ) gilt statt der
Bewegungsgleichung (11.42) die folgende Bewegungsgleichung (s. §10.6):
) gilt statt der
Bewegungsgleichung (11.42) die folgende Bewegungsgleichung (s. §10.6):
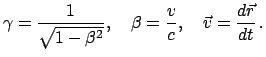
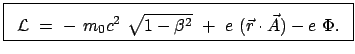
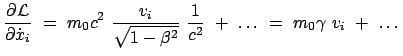
![]() const.,
const., ![]() ,
, ![]() ein. Die kinetische und die
potentielle Energie sind:
ein. Die kinetische und die
potentielle Energie sind:
![]() in der Lgrangefunktion
in der Lgrangefunktion
![]() nicht explizit vorkommt, ist
die zugehörige Lagrangegleichung 2. Art besonders einfach. Da
nicht explizit vorkommt, ist
die zugehörige Lagrangegleichung 2. Art besonders einfach. Da
![]() in dieser nicht auftritt, ist
in dieser nicht auftritt, ist
![]() eine Konstante der Bewegung. Vergleich
mit Gl. (6.19) zeigt, daß dies die
eine Konstante der Bewegung. Vergleich
mit Gl. (6.19) zeigt, daß dies die ![]() -Komponente des Drehimpulses ist.
-Komponente des Drehimpulses ist.
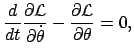
![$\displaystyle \frac{d}{dt} \left\{ \frac{m}{2} \left[ R^2 \dot{\theta}^2 + ...
..._{z}}
{m^2R^2 \sin^2 \theta} \right] + mgR \cos\theta \right\} = 0 .
$](img3133.gif)
![\begin{displaymath}\begin{array}{lclclcl} E & = & \frac{m}{2} \left[ R^2 \dot{...
...i}^{2} \right] & + & mgR \cos\theta & = & T + U . \end{array}\end{displaymath}](img3134.gif)
![]() entspricht
dem Glockenkörper,
entspricht
dem Glockenkörper, ![]() dem Klöppel. Die zweckmäßigsten Koordinaten
sind die
beiden Winkel
dem Klöppel. Die zweckmäßigsten Koordinaten
sind die
beiden Winkel
![]() und
und
![]() . In ihnen werden die
Kartesischen Koordinaten der
beiden Massenpunkte, danach die kinetische und potentielle Energie und die
Lagrangefunktion ausgedrückt:
. In ihnen werden die
Kartesischen Koordinaten der
beiden Massenpunkte, danach die kinetische und potentielle Energie und die
Lagrangefunktion ausgedrückt:
![\begin{displaymath}
\begin{array}{ccccl}
\left[ (1 + \mu) \omega_{0}^{2} - \...
...u) \omega_{0}^{2} - \omega^2) \right] B & = & 0 .
\end{array}\end{displaymath}](img3166.gif)
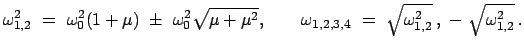
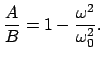
![]() leicht gegenüber
leicht gegenüber ![]() ist.
ist.
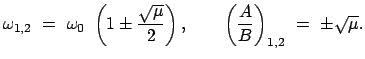
![\includegraphics[height=4cm]{K11dp2}](img3174.gif)
![\includegraphics[height=6cm]{K11dp3}](img3175.gif)
![]() -mal schwächer an das zweite gekoppelt ist als umgekehrt. Darum
ist auch die
Amplitude
-mal schwächer an das zweite gekoppelt ist als umgekehrt. Darum
ist auch die
Amplitude
![]() -mal kleiner als
-mal kleiner als ![]() . Statt der
imaginären Exponentialfunktionen benützen wir nun
trigonometrische Funktionen:
. Statt der
imaginären Exponentialfunktionen benützen wir nun
trigonometrische Funktionen:
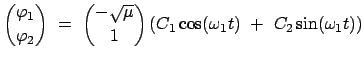
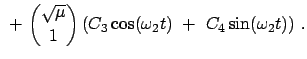
![]() .
. 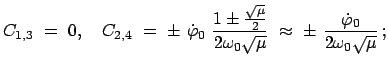
![]()
![]() den Argumenten
den Argumenten
![]() mit
mit
![]() .
Zusammen mit der Zeitableitung von (11.62) erhält man zu diesen
Werten
.
Zusammen mit der Zeitableitung von (11.62) erhält man zu diesen
Werten
![]() folgende Punkte in der
folgende Punkte in der
![]() bzw.
bzw.
![]() -Ebene:
-Ebene:
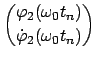
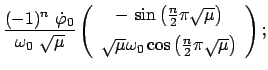
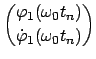
![$\displaystyle \frac{(-1)^n \dot{\varphi}_0}{\omega_{0} \sqrt{\mu}} \vspace{...
...eft(\frac{n}{2} + \frac{1}{4}\right) \pi \sqrt{\mu}
\right] \end{array}\right).$](img3198.gif)
![\includegraphics[width=16cm]{K11dp5}](img3200.gif)
![]() -Potenz wird das obige System
(11.65) in eine rein
algebraische Gleichung transformiert:
-Potenz wird das obige System
(11.65) in eine rein
algebraische Gleichung transformiert:
![]() aus Gln. (11.64) und (11.65) werden nun zu einem Vektor
zusammengefasst und dieser wird nach den Eigenvektoren
aus Gln. (11.64) und (11.65) werden nun zu einem Vektor
zusammengefasst und dieser wird nach den Eigenvektoren ![]() entwickelt:
entwickelt:
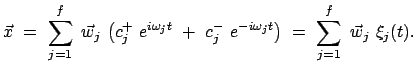
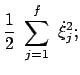
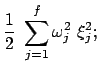
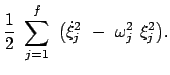
![]() gesetzt und folgende Abkürzungen eingeführt:
gesetzt und folgende Abkürzungen eingeführt:
![]() und
und
![]() . Die resultierenden Bewegungsgleichungen sind:
. Die resultierenden Bewegungsgleichungen sind:
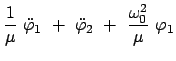
![$\displaystyle = \left( \begin{array}{cc} 1/\mu & 1 [2mm] 1 & 1 \end{array} \right) ,$](img3257.gif) P
P![$\displaystyle = \left( \begin{array}{cc} \omega_0^2 / \mu & 0 [2mm] 0 & \omega_0^2 \end{array} \right)
$](img3258.gif)
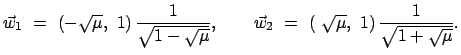
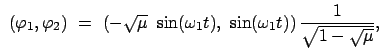
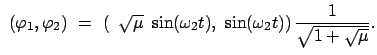
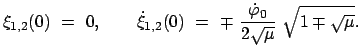
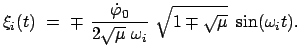
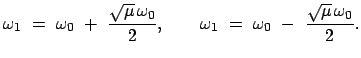
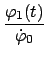
![$\displaystyle \
\frac{ 2 \sin (\omega_1 t) + 2 \sin (\omega_2 t) - \sqrt{\mu} \
[ \sin (\omega_1 t) - \sin (\omega_2 t)]}{(4 - \mu) \omega_0} ,$](img3273.gif)
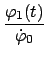
![$\displaystyle \
\frac{- 2 \sin (\omega_1 t) + 2 \sin (\omega_2 t) + \sqrt{...
...sin (\omega_1 t) + \sin (\omega_2 t)]}{(4 - \mu) \omega_0 \sqrt{\mu}} .$](img3274.gif)
![]() gegen 4 vernachläßigt, im Zähler der Term prorportional
zu
gegen 4 vernachläßigt, im Zähler der Term prorportional
zu
![]() . Dieses Resultat stimmt mit der ersten Zeile von Gl. (11.62) überein.
. Dieses Resultat stimmt mit der ersten Zeile von Gl. (11.62) überein.
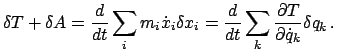
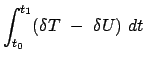
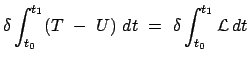
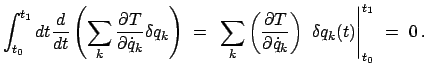
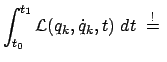 Extr.
Extr.
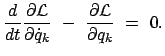
![]() Massenpunkten lautet:
Massenpunkten lautet:
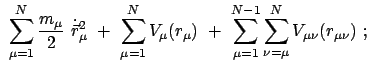
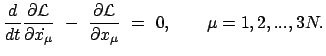
![]() ab:
ab:
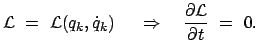
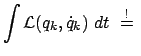 Extr
Extr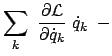
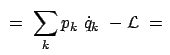 const.
const.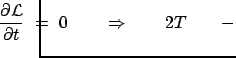
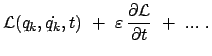
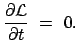
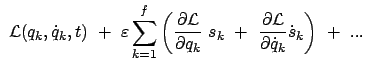
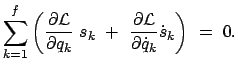
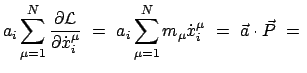 const.
const.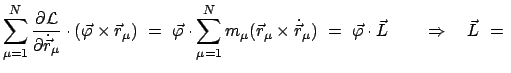 const.
const.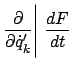
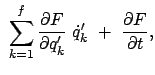
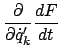
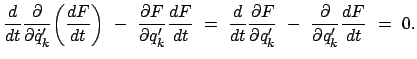
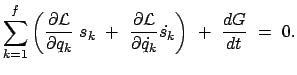
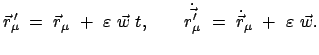
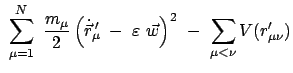
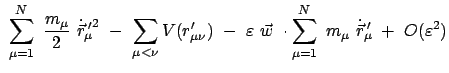
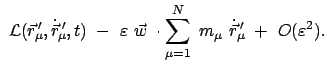
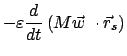
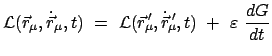
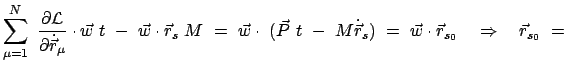 const.
const.