Unterabschnitte
In einem starren Körper (E. rigid body) bleiben definitionsgemäß die
relativen Abstände aller Punkte konstant,
 const. const. |
(91) |
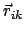 ist der Abstand der Punkte
ist der Abstand der Punkte
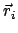 und
und
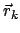 . Die
durch die Vektoren
. Die
durch die Vektoren
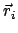 bezeichneten
Punkte mögen die Lage der Gitterpunkte (z.B. in einem Kristallgitter)
bezeichnen oder die Lage der Punkte, die man in einem kontinuierlich
gedachten Körper anzeichnet (s. Abb. 9.1).
bezeichneten
Punkte mögen die Lage der Gitterpunkte (z.B. in einem Kristallgitter)
bezeichnen oder die Lage der Punkte, die man in einem kontinuierlich
gedachten Körper anzeichnet (s. Abb. 9.1).
Die Bewegung des ganzen Körpers wird durch die dreier nicht kollinearer
Punkte
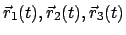 dieses
Körpers beschrieben.
Da die relativen Abstände der drei Punkte konstant sind, bleiben
9 Koordinaten - 3 Nebenbedingungen = 6 Freiheitsgrade.
Zu dieser Zahl kommt man auch über folgende geometrische Überlegung:
Die Bewegung des ersten Punktes, die Translation genannt wird, wird
durch 3 Parameter angegeben.
dieses
Körpers beschrieben.
Da die relativen Abstände der drei Punkte konstant sind, bleiben
9 Koordinaten - 3 Nebenbedingungen = 6 Freiheitsgrade.
Zu dieser Zahl kommt man auch über folgende geometrische Überlegung:
Die Bewegung des ersten Punktes, die Translation genannt wird, wird
durch 3 Parameter angegeben.
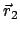 kann sich nur mehr auf der Oberfläche der Kugel vom Radius
kann sich nur mehr auf der Oberfläche der Kugel vom Radius
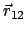 bewegen; dies gibt zwei weitere Parameter.
bewegen; dies gibt zwei weitere Parameter.
 kann sich nur mehr auf
einem Kreis (von gegebenem Radius) in einer Ebene senkrecht zur Verbindungsachse
von
kann sich nur mehr auf
einem Kreis (von gegebenem Radius) in einer Ebene senkrecht zur Verbindungsachse
von
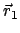 und
und
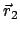 bewegen; dies wird durch den 6. Parameter beschrieben.
bewegen; dies wird durch den 6. Parameter beschrieben.
Wir können über die Bewegung eines starren Körpers einige allgemeine Aussagen
machen:
Satz 9.1: Die allgemeinste Bewegung eines starren Körpers besteht aus einer
Translation und einer Rotation.
Dazu wählen wir einen Punkt des Körpers (z.B.
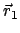 ) als Bezugspunkt.
Die Translation entspricht dem Verbindungsvektor von der Anfangslage
) als Bezugspunkt.
Die Translation entspricht dem Verbindungsvektor von der Anfangslage
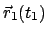 zur Endlage
zur Endlage
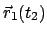 . Die Bewegung der
übrigen Punkte des Körpers, also insbesondere von
. Die Bewegung der
übrigen Punkte des Körpers, also insbesondere von
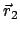 und
und
 wird durch ebendieselbe Translation plus eine
Drehung um eine durch
wird durch ebendieselbe Translation plus eine
Drehung um eine durch
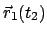 gehende Achse wiedergegeben.
Translationsvektor und Drehvektor enthalten je 3 Parameter; dies gibt wieder
die vorerwähnten 6 Freiheitsgrade.
gehende Achse wiedergegeben.
Translationsvektor und Drehvektor enthalten je 3 Parameter; dies gibt wieder
die vorerwähnten 6 Freiheitsgrade.
Der Satz wird im folgenden für infinitesimale Bewegung bewiesen. Wir betrachten
die 3 Punkte
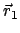 ,
,
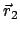 ,
,
 und ihre Geschwindigkeiten
und ihre Geschwindigkeiten
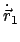 ,
,
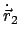 ,
,
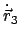 . Da
. Da
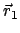 als
Bezugspunkt gewählt worden ist, ist
als
Bezugspunkt gewählt worden ist, ist
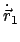 die
Translationsgeschwindigkeit. Für Punkt
die
Translationsgeschwindigkeit. Für Punkt
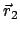 gilt
gilt
 const. const. |
(92) |
Da
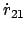 auf
auf
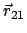 senkrecht steht, kann man einen Drehvektor
einführen (Abb. 9.2):
senkrecht steht, kann man einen Drehvektor
einführen (Abb. 9.2):
![$\displaystyle \dot{\vec r}_{21} = [\vec \omega, \vec r_{21}] \qquad \dot{\vec r}_{2} = \dot{\vec r}_{1} + [\vec \omega, \vec{r}_{2}-\vec{r}_{1}].$](img1997.gif) |
(93) |
Satz 9.2: Die Winkelgeschwindigkeit
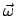 ist für alle Punkte des
Körpers gleich.
ist für alle Punkte des
Körpers gleich.
Auch für den Abstand
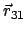 gelten analoge Berechnungen wie in Gl. (9.2),
sodaß wir wieder wie in Gl. (9.3) einen Drehvektor
gelten analoge Berechnungen wie in Gl. (9.2),
sodaß wir wieder wie in Gl. (9.3) einen Drehvektor
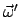 einführen können.
einführen können.
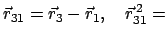 const. const.![$\displaystyle \quad \dot{\vec r}_{3} = \dot{\vec r}_{1} + [\vec{\omega}', \vec{r}_{3} - \vec{r}_{1}].$](img2008.gif) |
(94) |
Aus
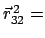 const. folgt, mit (9.3) und (9.4), daß
const. folgt, mit (9.3) und (9.4), daß
 ist:
ist:
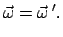 |
(95) |
Da die Vektoren
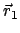 ,
,
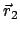 ,
,
 in weitem Maße
beliebig sind, kann immer erreicht werden, daß ihre Kombination in den
vorhergehenden Ausdrücken ungleich Null und nicht normal zu
in weitem Maße
beliebig sind, kann immer erreicht werden, daß ihre Kombination in den
vorhergehenden Ausdrücken ungleich Null und nicht normal zu
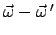 ist. Also muß diese Differenz der
Winkelgeschwindigkeitsvektoren Null sein.
ist. Also muß diese Differenz der
Winkelgeschwindigkeitsvektoren Null sein.
Satz 9.3: Die Winkelgeschwindigkeit
 ist unabhängig vom Bezugspunkt;
also nur durch die Bewegung charakterisiert.
ist unabhängig vom Bezugspunkt;
also nur durch die Bewegung charakterisiert.
Auch für
 als Bezugspunkt muß eine Gleichung analog zu (9.3) gelten.
Wir nehmen an, die zugehörige Winkelgeschwindigkeit sei
als Bezugspunkt muß eine Gleichung analog zu (9.3) gelten.
Wir nehmen an, die zugehörige Winkelgeschwindigkeit sei
 und
setzen dann Gln. (9.3), (9.4), (9.5) ein.
und
setzen dann Gln. (9.3), (9.4), (9.5) ein.
Sei
 Bezugspunkt:
Bezugspunkt:
Die Winkelgeschwindigkeit
 ist also eine für die Bewegung des Körpers
charakteristische Größe; mit ihrer Hilfe läßt sich die Bewegung jedes Punktes
berechnen.
ist also eine für die Bewegung des Körpers
charakteristische Größe; mit ihrer Hilfe läßt sich die Bewegung jedes Punktes
berechnen.
Satz 9.4: Die Winkelgeschwindigkeit
 läßt sich aus der Geschwindigkeit dreier
Punkte des Körpers berechnen., (Gl. (9.6)).
läßt sich aus der Geschwindigkeit dreier
Punkte des Körpers berechnen., (Gl. (9.6)).
Wir bilden
Wegen (9.4) ist der erste Term der rechten Seite Null.
Daher gilt
![$\displaystyle \vec{\omega} = - \frac{[\dot{\vec r}_{2}-\dot{\vec r}_{1} , \dot{...
...ec r}_{1}]}{(\vec{r}_{2}-\vec{r}_{1} , \dot{\vec r}_{3}-\dot{\vec r}_{1})} .$](img2026.gif) |
(96) |
Während die Winkelgeschwindigkeit vom Bezugspunkt unabhängig ist und ausschließlich
von der Bewegung bestimmt wird,ist die Translationsgeschwindigkeit im allgemeinen
für die Wahl jedes Bezugspunktes verschieden. Doch gibt es für jede Bewegung eine
ausgezeichnete Achse, die Schrotachse. Für jeden Punkt der Schrotachse als
Bezugspunkt ist die Translation parallel der Winkelgeschwindigkeit. Um die
Schrotachse aufzusuchen, gehen wir von einem beliebigen Bezugspunkt aus. Die
zugehörige Translationsgeschwindigkeit wird in eine Komponente senkrecht und eine
parallel zur Winkelgeschwindigkeit
 zerlegt (Abb. 9.3).
zerlegt (Abb. 9.3).
Wir suchen nun einen Bezugspunkt
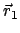 , der durch die folgenden zwei
Bedingungen festgelegt ist
, der durch die folgenden zwei
Bedingungen festgelegt ist
Ein solcher Bezugspunkt läßt sich immer finden. Denn multipliziert man die
linke der obigen Gleichungen vektoriell mit
 und benutzt dann
die rechte, findet man
und benutzt dann
die rechte, findet man
Die Translationsgeschwindigkeit
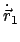 dieses Punktes ist gemäß (9.3)
und den vorhergehenden Gln.
Der Punkt
dieses Punktes ist gemäß (9.3)
und den vorhergehenden Gln.
Der Punkt
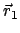 ist also ein Bezugspunkt, dessen Translationsgeschwindigkeit
ist also ein Bezugspunkt, dessen Translationsgeschwindigkeit
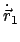 parallel zu
parallel zu
 ist. Die Menge aller Punkte,
für die dies gilt, ist die Schrotachse
ist. Die Menge aller Punkte,
für die dies gilt, ist die Schrotachse
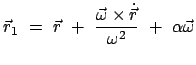 |
(97) |
Berechnet man nämlich für alle diese Bezugspunkte die
Translationsgeschwindigkeit
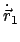 wie vor Gl. (9.7), dann kommt aus dem einen zusätzlichen Term
wie vor Gl. (9.7), dann kommt aus dem einen zusätzlichen Term
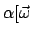 ,
,
![$ \vec{\omega} ] = 0$](img2039.gif) .
.
Für alle Punkte der Schrotachse ist die Bewegung des Körpers eine Translation
in Richtung der Schrotachse und eine Drehung um diese; eine solche Bewegung
heißt Schraubbewegung.
Im Laufe der Bewegung ändert sich auch im allgemeinen die Schrotachse. Sie
erzeugt dabei eine Regelfläche. (Bewegt man eine Gerade im Raum, so überstreicht
sie eine Fläche, eben die Regelfläche.) Verfolgt man die Bewegung der
Schrotachse vom mitbewegten System aus, dann erhält man dabei auch eine Regelfläche,
die aber im allgemeinen von der ersten verschieden sein wird. Die beiden
Regelflächen berühren sich immer entlang der Schrotachse; sie rollen aber nicht nur
aufeinander, sondern gleiten gegeneinander längs der Berührungsgeraden: Sie
'schroten' aufeinander.
Als Beispiel betrachten wir einen Kreiszylinder, der mit konstanter Winkelgeschwindigkeit
 um seine Achse rotiert, während diese Achse mit der konstanten
Geschwindigkeit
um seine Achse rotiert, während diese Achse mit der konstanten
Geschwindigkeit
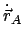 parallel zu sich selbst fliegt,
s. Abb. 9.4. Für den
Bezugspunkt
parallel zu sich selbst fliegt,
s. Abb. 9.4. Für den
Bezugspunkt
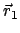 heben sich
heben sich
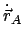 und
und
![$ [\vec{\omega},\vec{r}_{1}]$](img2041.gif) auf. Dies ist die Schrotachse; die Translationsgeschwindigkeit ist hier Null
auf. Dies ist die Schrotachse; die Translationsgeschwindigkeit ist hier Null
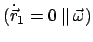 . Die raumfeste Regelfläche
ist eine Ebene,
die körperfeste ein Zylinder (Abb. 9.4, in Strichen gezeichnet), der auf
der Ebene rollt. Hat
. Die raumfeste Regelfläche
ist eine Ebene,
die körperfeste ein Zylinder (Abb. 9.4, in Strichen gezeichnet), der auf
der Ebene rollt. Hat
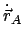 auch eine Komponente in Richtung der
Zylinderachse, dann gleitet der körperfeste Zylinder auf der Ebene längs
der momentan berührenden Erzeugenden, er 'schrotet'.
auch eine Komponente in Richtung der
Zylinderachse, dann gleitet der körperfeste Zylinder auf der Ebene längs
der momentan berührenden Erzeugenden, er 'schrotet'.
Abbildung 9.4:
Translation und Rotation eines Zylinders: Schrotachse, raumfeste
und körperfeste Regelfläche.
|
![\includegraphics[scale=0.83]{k9_rot_trans_zyl}](img2043.gif) |
Der starre Körper wird als ein Ensemble von 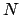 Massenpunkten mit Lagen
Massenpunkten mit Lagen
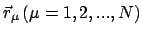 betrachtet. Die Bedingung der Starrheit
lautet dann (vgl. Gl. (9.1)):
Die Bewegungsgleichungen für diese Massenpunkte sind die Lagrangeschen
Gleichungen 1. Art, Gln. (11.16), s. a. (6.8):
betrachtet. Die Bedingung der Starrheit
lautet dann (vgl. Gl. (9.1)):
Die Bewegungsgleichungen für diese Massenpunkte sind die Lagrangeschen
Gleichungen 1. Art, Gln. (11.16), s. a. (6.8):
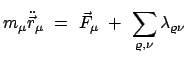
grad
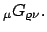
Da in
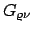 für gegebenes
für gegebenes 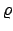 und
und 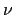 nur die
Koordinaten der beiden Vektoren
nur die
Koordinaten der beiden Vektoren
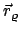 und
und
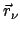 vorkommen, liefert grad
vorkommen, liefert grad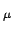 nur dann einen nicht verschwindenden Beitrag,
wenn
nur dann einen nicht verschwindenden Beitrag,
wenn 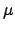 mit
mit 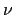 oder
oder 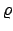 übereinstimmt:
übereinstimmt:
grad
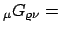
grad
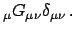
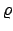 in
in 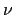 umgetauft. Die beiden Summen lassen sich wegen
umgetauft. Die beiden Summen lassen sich wegen
grad

grad
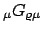
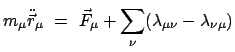 grad grad |
(98) |
Die Zwangskräfte
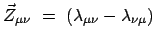
grad
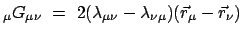
wirken in Richtung der Verbindungslinie der jeweiligen Punkte, sind also
Zentralkräfte. Die in Kap. 7 entwickelte Theorie der Systeme von Massenpunkten
läßt sich daher auf die Bewegungsgleichungen (9.8) anwenden. Natürlich wäre
es sehr umständlich, diese für praktische Berechnungen zu verwenden, doch
können wir darauf einige Untersuchungen grundsätzlicher Art aufbauen.
In §7.2.2 ist der Satz über den Zusammenhang zwischen der Änderung des
Drehimpulses und dem Moment der äußeren Kräfte abgeleitet worden.
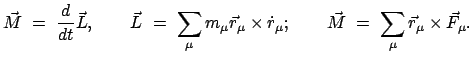 |
(99) |
Dabei ist vorausgesetzt worden, daß das Bezugssystem ein Inertialsystem ist
und daß die inneren Kräfte Zentralkräfte sind, die nur vom relativen Abstand der
jeweiligen zwei Punkte abhängen.
Für die Anwendung dieses Satzes auf die Bewegung des starren Körpers ist es
nötig, seine Gültigkeit auf bewegte und sogar beschleunigte Bezugspunkt zu erweitern.
Dies wird uns dann gestatten, eine Formel für den Drehimpuls der Relativbewegung anzugeben,
in die der Trägheitstensor eingeht.
Wir gehen zunächst zu einem neuen Bezugspunkt
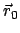 über, der ebenfalls im
Inertialsystem ruht:
Da sich bei diesem Wechsel des Bezugspunktes physikalisch nichts ändert, muß
auch hier gelten
über, der ebenfalls im
Inertialsystem ruht:
Da sich bei diesem Wechsel des Bezugspunktes physikalisch nichts ändert, muß
auch hier gelten
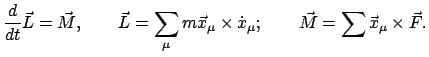 |
(910) |
Ist der Bezugspunkt bewegt, dann gilt im allgemeinen dieser Zusammenhang nicht.
Ist aber der Bezugspunkt der Schwerpunkt
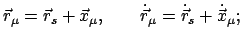 |
|
|
(911) |
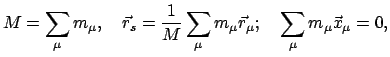 |
|
|
|
dann gilt wieder
bei beliebiger Bewegung des Schwerpunktes. Zum Beweis dieser Relation werden
Gln. (9.11) in (9.9) eingesetzt
In der letzten Zeile heben sich die Exprodukte, die
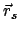 enthalten,
gemäß der Bewegungsgleichung für den Schwerpunkt; die jeweils links und
rechts verbleibenden Terme geben das obige Resultat (9.12).
enthalten,
gemäß der Bewegungsgleichung für den Schwerpunkt; die jeweils links und
rechts verbleibenden Terme geben das obige Resultat (9.12).
Die Gleichungen (9.10) verwendet man vor allem bei der Untersuchung
der Bewegung eines Körpers,
der in einem Punkt in einem Inertialsystem fixiert ist; Gl. (9.12) bei der
eines Körpers, der nirgends festgehalten ist. Obwohl diese Gleichungen etwas
verschiedene Aussagen enthalten, ist ihr formales Aussehen gleich. Gerade darauf
bauen die weiteren Ableitungen auf. Da
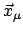 immer vom Bezugspunkt aus
gerechnet wird und der Körper starr ist, gilt wie in Gl. (9.3)
immer vom Bezugspunkt aus
gerechnet wird und der Körper starr ist, gilt wie in Gl. (9.3)
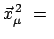
const.
![$\displaystyle \quad \Rightarrow \quad \dot{\vec x}_{\mu} = \
[\vec{\omega}, \vec{x}_{\mu}] .
$](img2075.gif)
Für das weitere ist es zweckmäßiger, auf die Tensorschreibweise überzugehen
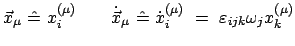 |
(913) |
Diese Ausdrücke werden in Gln. (9.10) oder (9.12) eingesetzt:
Der Zusammenhang zwischen Drehimpuls 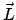 und Drehvektor
und Drehvektor
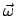
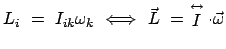 |
(914) |
wird durch den Trägheitstensor
![$\displaystyle I_{ik} = \sum_{\mu} m_{\mu} \left[\delta_{ik} x^{(\mu)}_{s} x^{(\mu)}_{s} - x^{(\mu)}_{i} x^{(\mu)}_{k} \right]$](img2081.gif) |
(915) |
vermittelt. Damit wird aus Gln. (9.10) bzw. (9.12)
 |
(916) |
Diese Gleichung gilt wegen der Voraussetzungen für Gln. (9.10) und (9.12)
nur dann, wenn für sie als Bezugspunkt entweder ein Punkt, der in einem
Inertialsystem ruht und in dem der Körper fixiert ist, oder der beliebig
bewegte Schwerpunkt des Körpers gewählt wird.
Da bei all diesen Betrachtungen ein Koordinatensystem
benützt worden ist, dessen Koordinatenachsen immer parallel denen des raumfesten
Systems sind, handelt es sich nicht um körperfeste Systeme. Daher werden im allgemeinen
die Vektoren
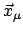 zeitabhängig sein und daher auch die Komponenten des
Trägheitstensors (9.15).
zeitabhängig sein und daher auch die Komponenten des
Trägheitstensors (9.15).
Für Systeme von Massenpunkten gelten der Schwerpunktsatz, Gl. (7.8) und der
Drehimpulssatz, Gl. (7.15):
Da es beim starren Körper keine innere Bewegung gibt, genügt es für
Gleichgewicht, daß sich die Wirkungen der äußeren Kräfte aufheben.
Ist der Körper anfänglich in Ruhe, d.h. im Gleichgewicht, dann bleibt er es
auch weiterhin. Im ebenen Fall hat man zwei Kräfte- und eine Momentengleichung.
Diese Bedingungen werden vor allem auch verwendet in der Statik der
Fachwerke. Es ist wesentlich, daß nicht nur die Summe der Kräfte, sondern
auch die Summe der Momente Null ist. Denn z.B. für ein Kräftepaar verschwindet
die Summe der Kräfte, nicht aber deren Moment.
Als ein Beispiel betrachten wir einen homogenen Stab, der an einer Wand lehnt
(Abb. 9.5). Wir suchen den Neigungswinkel, bei dem dieser gerade noch von den
Kräften der Haftreibung gehalten wird. Man kann annehmen, daß das Gewicht 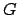 nur im Schwerpunkt
nur im Schwerpunkt  angreift. Die Rektionskräfte
angreift. Die Rektionskräfte 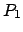 ,
,  und die
Reibungskräfte
und die
Reibungskräfte 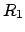 ,
, 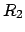 wirken nur an den Endpunkten. Die Kräfte
und ihre Kraftarme sind
wirken nur an den Endpunkten. Die Kräfte
und ihre Kraftarme sind
Abbildung:
Ein Stab lehnt an einer Wand. Die Reibungskräfte verhindern das Abrutschen.
|
![\includegraphics[scale=0.83]{k9_stabanwand}](img2097.gif) |
Die Gleichgewichtsbedingungen (9.17) und (9.18) liefern
![$\displaystyle \vec{F}_{0} + \vec{F}_{1} + \vec{F}_{2} = 0:\;\left\{ \begin{arra...
...cc} - R_{1} + P_{2} = 0 , [0.5em] P_{1} + R_{2} = G . \end{array}\right.$](img2098.gif) |
(919) |
Wir nehmen weiter an, daß für die Reibungskräfte das Coulombsche
Reibungsgesetz gilt: Die Reibungskraft ist proportional der Normalkraft.
Die Normalkraft ist aber gleich groß wie die Reaktionskraft an diesem Punkt.
Daher können wir schreiben
 |
(921) |
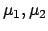 sind die Koeffizienten der Haftreibung für
den Stab längs des Bodens (der Wand). Obige Relationen werden in
Gln. (9.19) eingesetzt und das entstehende Gleichungssystem gelöst.
sind die Koeffizienten der Haftreibung für
den Stab längs des Bodens (der Wand). Obige Relationen werden in
Gln. (9.19) eingesetzt und das entstehende Gleichungssystem gelöst.
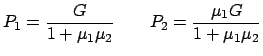 |
(922) |
Werden (9.21) und (9.22) in (9.20) eingesetzt, ergibt sich für den Neigungswinkel,
der gerade noch zulässig ist, ohne daß der Stab wegrutscht:
Der Stab steht stabil für Neigungswinkel
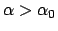 . Für diesen Fall
können die Kräfte aus den obigen Gleichungen nicht eindeutig bestimmt werden,
weil dann an Stelle der obigen Gleichung eine Ungleichung steht (Statisch unbestimmtes
System). Für
. Für diesen Fall
können die Kräfte aus den obigen Gleichungen nicht eindeutig bestimmt werden,
weil dann an Stelle der obigen Gleichung eine Ungleichung steht (Statisch unbestimmtes
System). Für
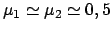 (Haftreibungskoeffizient für
Holz auf Holz) ist
(Haftreibungskoeffizient für
Holz auf Holz) ist
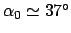 .
.
Der Trägheitstensor, s. Gl. (9.15),
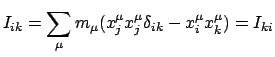 |
(923) |
ist ein symmetrischer Tensor zweiter Stufe. Als Matrix geschrieben, sieht er
so aus:
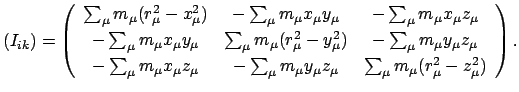 |
(924) |
Seine Elemente sind vom Bezugspunkt und von der Lage des Koordinatensystems
abhängig. Meist denkt man an ein körperfestes Koordinatensystem. 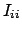 ,
die Elemente der Hauptdiagonale, heißen Trägheitsmomente;
,
die Elemente der Hauptdiagonale, heißen Trägheitsmomente; 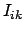 ,
die Elemente außerhalb der Hauptdiagonalen, heißen Deviationsmomente.
Die Bedeutung dieser Namen wird unten erläutert.
,
die Elemente außerhalb der Hauptdiagonalen, heißen Deviationsmomente.
Die Bedeutung dieser Namen wird unten erläutert.
Für eine kontinuierliche, durch die Dichtfunktion
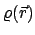 beschriebene
Massenverteilung, hat man statt (9.23)
beschriebene
Massenverteilung, hat man statt (9.23)
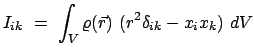 |
(925) |
Der Trägheitstensor kann durch eine Äquivalenztransformation mittels
einer Matrix 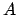 auf Hauptachsen transformiert werden:
auf Hauptachsen transformiert werden:
 |
(926) |
Dabei geht 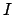 in Diagonalform über:
in Diagonalform über:
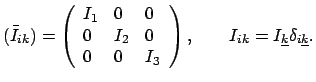 |
(927) |
(Nicht über
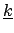 summieren !). Die Matrix
summieren !). Die Matrix 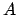 kann dabei reell orthogonal
gewählt werden. Die inverse Matrix
kann dabei reell orthogonal
gewählt werden. Die inverse Matrix 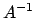 ist dann gleich der transponierten
Matrix
ist dann gleich der transponierten
Matrix  (vgl. Gln. (8.7)):
Eine Hauptachsentransformation wie oben angegeben stellt eine Drehung des Koordinatensystems dar.
(vgl. Gln. (8.7)):
Eine Hauptachsentransformation wie oben angegeben stellt eine Drehung des Koordinatensystems dar.
Die  heißen die Hauptträgheitsmomente; sie sind immer positiv (Beweis
am Ende dieses §).
heißen die Hauptträgheitsmomente; sie sind immer positiv (Beweis
am Ende dieses §).
Für den Trägheitstensor wie für jeden symmetrischen Tensor zweiter Stufe
kann eine geometrische Deutung gegeben werden. Wir ziehen einen dreidimensionalen
kartesischen Raum
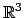 mit Punkten (oder Vektoren)
mit Punkten (oder Vektoren)
 heran. In diesem Raum
stellt der Ausdruck
heran. In diesem Raum
stellt der Ausdruck
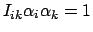 |
(928) |
einen Kegelschnitt dar, das Trägheitsellipsoid. Da 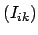 symmetrisch ist, sind die Eigenwerte reell
und die Transformationsmatrix
symmetrisch ist, sind die Eigenwerte reell
und die Transformationsmatrix 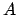 , die aus den Eigenvektoren aufgebaut ist und
die in Gl. (9.26) erwähnte Hauptachsentransformation vermittelt, kann orthogonal
gewählt werden:
Sie ist also eine Drehung auf ein Koordinatensystem, dessen Achsen mit denen
des Ellipsoids zusammenfällt:
, die aus den Eigenvektoren aufgebaut ist und
die in Gl. (9.26) erwähnte Hauptachsentransformation vermittelt, kann orthogonal
gewählt werden:
Sie ist also eine Drehung auf ein Koordinatensystem, dessen Achsen mit denen
des Ellipsoids zusammenfällt:
Abbildung:
a) Das Trägheitsellipsoid. b) Verschiedene Trägheitsellipsoide entsprechen
verschiedenen Stellen eines Körpers als Bezugspunkte.
|
[]
![\includegraphics[scale=0.63]{k9_treagheits_ellipso}](img2127.gif) []
[]
![\includegraphics[scale=0.54]{k9_versch_treagh_ell}](img2128.gif) |
Die Halbachsen des Ellipsoides haben die Länge
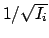 , s. Abb. 9.6(a).
Da die Werte der Elemente des Trägheitstensors auch von der Lage des Bezugspunktes
abhängen, muß man sich vorstellen, daß zu jedem Punkt des Körpers ein
anderes Trägheitsellipsoid gehört, s. Abb. 9.6(b).
, s. Abb. 9.6(a).
Da die Werte der Elemente des Trägheitstensors auch von der Lage des Bezugspunktes
abhängen, muß man sich vorstellen, daß zu jedem Punkt des Körpers ein
anderes Trägheitsellipsoid gehört, s. Abb. 9.6(b).
Daß alle Eigenwerte  nicht nur reell, sondern auch positiv sind, folgert
man daraus, daß die quadratische Form
nicht nur reell, sondern auch positiv sind, folgert
man daraus, daß die quadratische Form
immer positiv definit, also immer positiv ist. Die Summe ganz rechts besteht
aus mehreren Summanden, die nicht alle Null sein können, wenn nicht alle
Vektoren
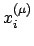 kollinear sind. Es gibt also keinen Vektor (außer
dem Nullvektor), für den die obige Summe Null oder negativ ist. Ist nun
kollinear sind. Es gibt also keinen Vektor (außer
dem Nullvektor), für den die obige Summe Null oder negativ ist. Ist nun
 ein Eigenvektor, und zwar der zum Eigenwert
ein Eigenvektor, und zwar der zum Eigenwert  ,
dann folgt weiter
,
dann folgt weiter
Durch diesen Satz wird der Trägheitstensor bezüglich eines beliebigen
Bezugspunktes in Beziehung gebracht zum Trägheitstensor bezüglich des
Schwerpunktes S (mit Koordinaten 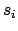 ).
).
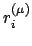 seien die
Koordinaten des Punktes
seien die
Koordinaten des Punktes
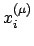 bezüglich S, Abb. 9.7.
bezüglich S, Abb. 9.7.
Abbildung 9.7:
Wechsel des Bezugspunkts. S ist der Schwerpunkt des Körpers.
|
![\includegraphics[scale=0.83]{k9_bezugssys_wechsel}](img2138.gif) |
Aus Gl. (9.23) erhält man damit
![$\displaystyle \hspace*{-6.45cm} I_{ik}\;\; =\;\; I_{ik}^{s}\; \;+\;\; M [s^{2} \delta_{ik} - s_{i}s_{k} ].$](img2142.gif) |
(929) |
Der Trägheitstensor bezüglich eines beliebigen Punktes ist gleich dem
Trägheitstensor bezüglich des Schwerpunktes plus dem Trägheitstensor der
in S vereinigten Gesamtmasse bezüglich des beliebigen Punktes.
Sehr oft benötigt man das Trägheitsmoment für eine Drehung um eine vorgegebene Achse. Diese
sei durch den Einheitsvektor  gegeben:
gegeben:
Dies wird in Gl. (9.14) eingesetzt
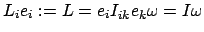 |
(930) |
mit
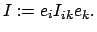 |
(931) |
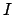 ist das Trägheitsmoment um
ist das Trägheitsmoment um  ;
; 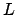 der Drehimpuls um
der Drehimpuls um  .
Vergleich von Gl. (9.30) mit
.
Vergleich von Gl. (9.30) mit 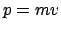 , Gl. (3.18),
zeigt, daß Drehimpuls, Trägheitsmoment und
Winkelgeschwindigkeit bei Rotation eines Körpers eine analoge Rolle spielen
wie Impuls, Masse und Geschwindigkeit bei der Bewegung eines Massenpunktes.
Der Ausdruck (9.23) wird in (9.31) eingesetzt
, Gl. (3.18),
zeigt, daß Drehimpuls, Trägheitsmoment und
Winkelgeschwindigkeit bei Rotation eines Körpers eine analoge Rolle spielen
wie Impuls, Masse und Geschwindigkeit bei der Bewegung eines Massenpunktes.
Der Ausdruck (9.23) wird in (9.31) eingesetzt
![$\displaystyle I = \sum_{\mu} m_{\mu} \left[ x_{s}^{(\mu)} x_{s}^{(\mu)} e_{i}e_...
...mu)})^{2} \right] = \sum_{\mu} m_{\mu} \left[ \varrho_{i}^{(\mu)} \right]^{2} .$](img2148.gif) |
(932) |
ist der Normalabstand des Punktes 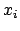 von der Drehachse
von der Drehachse  . Das
Trägheitsmoment einer Masse ist gleich Masse mal Quadrat des Normalabstandes
(vgl. die Ausdrücke in der Hauptdiagonale von Gl. (9.24)).
. Das
Trägheitsmoment einer Masse ist gleich Masse mal Quadrat des Normalabstandes
(vgl. die Ausdrücke in der Hauptdiagonale von Gl. (9.24)).
Wir setzen noch
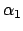 ist der Winkel zwischen dem Vektor
ist der Winkel zwischen dem Vektor  der Drehachse und der
der Drehachse und der
 -ten Hauptträgheitsachse. Dann bekommen wir
-ten Hauptträgheitsachse. Dann bekommen wir
Wir überschieben den Steinerschen Satz, Gl. (9.7), mit  und
und 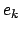 und bekommen
und bekommen
![\begin{displaymath}\begin{array}{cccccc} & e_{i}I_{ik}e_{k} & = & e_{i}I_{ik}^{s...
...2}] [2mm] = & I & = & I^{s} & + & M \varrho^{2}. \end{array}\end{displaymath}](img2156.gif) |
(933) |
Das Trägheitsmoment um eine beliebige Achse = Trägheitsmoment um
eine parallele Achse durch Schwerpunkt + Trägheitsmoment der Gesamtmasse im
Normalabstand der beiden Achsen (s. Abb. 9.8).
1cm
Abbildung 9.8:
Steinerscher Satz
|
![\includegraphics[scale=0.63]{k9_steiner_satz}](img2157.gif)
|
Abbildung 9.9:
Drehung eines Stabes
|
![\includegraphics[scale=0.63]{k9_drehung_stab}](img2158.gif)
|
Abbildung 9.10:
Drehung eines Rechtecks
|
![\includegraphics[scale=0.63]{k9_drehung_rechteck}](img2159.gif)
|
Das Trägheitsmoment eines Stabes (Gesamtmasse 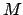 , Länge
, Länge 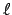 ) für Rotation um
eine Achse senkrecht durch einen Endpunkt (Abb. 9.9) ist nach (9.32)
) für Rotation um
eine Achse senkrecht durch einen Endpunkt (Abb. 9.9) ist nach (9.32)
 |
(934) |
oder mittels des Steinerschen Satzes (9.33)
Das Trägheitsmoment eines Rechteckes um eine senkrechte Achse durch den
Mittelpunkt (Abb. 9.10) ist
Wir zerlegen die Bewegung des Körpers in eine Translation (des Bezugspunktes
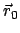 ) und in eine Rotation gegeben durch den Drehvektor
) und in eine Rotation gegeben durch den Drehvektor
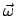 .
Die Bewegung des Punktes
.
Die Bewegung des Punktes
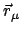 ist (vgl. Gl. (9.13))
ist (vgl. Gl. (9.13))
Die kinetische Energie des Körpers ist
Gesamte kinetische Energie = Energie der Translation der im Bezugspunkt
vereinigten Gesamtmasse + Energie der Rotation des Körpers + Wechselwirkungsenergie
zwischen Translation und Rotation.
Für den Schwerpunkt als Bezugspunkt ist die Wechselwirkungsenergie
Null:
Ist ein Punkt des Körpers fixiert, dann wählt man diesen als Bezugspunkt;
damit sind Translations- und Wechselwirkungsenergie Null;
Die Rotationsenergie kann noch umgeformt werden durch die Einführung des
Trägheitstensors gemäß. Gln. (9.13) und (9.23)
Für die letzte Umformung wurde Gl. (9.14) herangezogen.
Für die Rotation um eine Achse  wird daraus wegen Gln. (9.30)
und (9.31)
wird daraus wegen Gln. (9.30)
und (9.31)
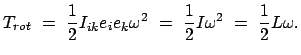 |
(936) |
Auch hier fällt die Ähnlichkeit mit
 auf.
auf.
Die Änderung des dynamischen Zustandes des Körpers durch das Moment der
äußeren Kräfte ist im raumfesten Koordinatensystem in Gl. (9.16) angegeben
worden. Diese Gleichung hat den Nachteil, daß der Trägheitstensor im
raumfesten System im allgemeinen nicht zeitlich konstant ist. Wohl aber sind seine
Komponenten im körperfesten System konstant. Daher ist in diesem System die
Gleichung für die Änderung des Drehimpulses einfacher
Das körperfeste System ist im allgemeinen ein beschleunigtes Bezugssystem.
Gemäß Gln. (8.5), (8.9) und (8.32b), (8.33) gilt
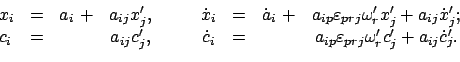 |
(939) |
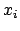 bzw.
bzw. 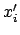 sind die Koordinaten ein- und desselben Punktes im raum-
bzw. körperfesten System.
sind die Koordinaten ein- und desselben Punktes im raum-
bzw. körperfesten System. 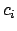 bzw.
bzw. 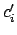 sind die entsprechenden
Koordinaten eines echten Vektors.
sind die entsprechenden
Koordinaten eines echten Vektors.
Die letzte der obigen Gleichungen wird für die Transformation des Drehimpulses
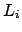 in den nachfolgenden Gleichungen verwendet. Zusammen mit Gl. (9.37) gibt das:
in den nachfolgenden Gleichungen verwendet. Zusammen mit Gl. (9.37) gibt das:
In Gl. (9.41) wird die Bewegung zuerst im körperfesten System berechnet und dann
durch die Transformation mittels 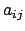 zum Moment im raumfesten System in
Beziehung gesetzt. Gl. (9.42) ist vollständig im körperfesten
System gerechnet. Gl. (9.43) ist dieselbe in symbolischer Form.
Nun wird das körperfeste Koordinatensystem so gewählt, daß der
Trägheitstensor Diagonalform, Gl. (9.27), annimmt (über unterstrichene doppelte Indices
nicht summieren !)
zum Moment im raumfesten System in
Beziehung gesetzt. Gl. (9.42) ist vollständig im körperfesten
System gerechnet. Gl. (9.43) ist dieselbe in symbolischer Form.
Nun wird das körperfeste Koordinatensystem so gewählt, daß der
Trägheitstensor Diagonalform, Gl. (9.27), annimmt (über unterstrichene doppelte Indices
nicht summieren !)
Dies sind die Eulerschen Gleichungen für die Bewegung eines starren Körpers.
Die in 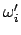 nichtlinearen Terme entsprechen dem Moment der Zentrifugalkraft.
nichtlinearen Terme entsprechen dem Moment der Zentrifugalkraft.
Wir betrachten Gl. (9.43) für den Fall, daß der Körper auf einer fest gelagerten
Achse steckt. Diese sei die 3'-Achse. Dann ergibt sich unter Beachtung von
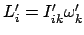
Die Bewegunggleichung im körperfesten System (9.42) gibt dann:
Die letzte Gleichung kann sofort integriert werden, da das Moment 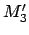 von der
Antriebskraft herrührt und daher im Prinzip eine gegebene Funktion der Zeit
ist. Die so erhaltene Lösung
von der
Antriebskraft herrührt und daher im Prinzip eine gegebene Funktion der Zeit
ist. Die so erhaltene Lösung
 wird in die linken Seiten der beiden
vorhergehenden Gleichungen eingesetzt. Dies gibt Momente
wird in die linken Seiten der beiden
vorhergehenden Gleichungen eingesetzt. Dies gibt Momente
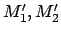 , die
die
, die
die 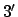 -Achse abzudrehen suchen und von den Lagern aufgefangen werden müssen.
Diese Momente werden von den Deviationsmomenten des Trägheitstensors verursacht.
Daher deren Name. Sie resultieren aus einer unsymmetrischen Montierung des Körpers.
-Achse abzudrehen suchen und von den Lagern aufgefangen werden müssen.
Diese Momente werden von den Deviationsmomenten des Trägheitstensors verursacht.
Daher deren Name. Sie resultieren aus einer unsymmetrischen Montierung des Körpers.
Abb. 9.11(a) gibt ein Beispiel:
Eine Stange rotiert um die 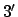 -Achse. Sie steht nicht vollkommen senkrecht zu
dieser, daher suchen die Zentrifugalkräfte die Stange in die senkrechte
Stellung zu ziehen und erzeugen ein Moment um die
-Achse. Sie steht nicht vollkommen senkrecht zu
dieser, daher suchen die Zentrifugalkräfte die Stange in die senkrechte
Stellung zu ziehen und erzeugen ein Moment um die 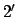 -Achse. Ist die
Rotation um die
-Achse. Ist die
Rotation um die 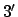 -Achse nicht gleichförmig, entsteht auch noch ein Moment
um die
-Achse nicht gleichförmig, entsteht auch noch ein Moment
um die  -Achse.
-Achse.
Abbildung 9.11:
a) Deviation eines unsymmetrisch gelagerten Stabes. b) Physikalisches Pendel
|
[]
![\includegraphics[scale=0.8]{k9_deviation}](img2207.gif) []
[]
![\includegraphics[scale=0.8]{k9_phys_pendel}](img2208.gif) |
Sind die Deviationsmomente
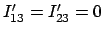 , dann
, dann
 .
Der Körper kann um eine solche Achse rotieren, ohne festgehalten werden zu
müssen. Eine solche Achse heißt eine freie Achse des Körpers. In diesem
Fall ist der Drehimpuls der Achse parallel gerichtet.
Wir haben dann:
.
Der Körper kann um eine solche Achse rotieren, ohne festgehalten werden zu
müssen. Eine solche Achse heißt eine freie Achse des Körpers. In diesem
Fall ist der Drehimpuls der Achse parallel gerichtet.
Wir haben dann:
Für die letzte Gleichung hat man wieder die Analogie von
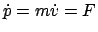 .
Daß Gln. (9.45) auch im raumfesten System gelten, sieht man durch Transformation
ins raumfeste System. Dabei ergibt sich auch noch, daß
.
Daß Gln. (9.45) auch im raumfesten System gelten, sieht man durch Transformation
ins raumfeste System. Dabei ergibt sich auch noch, daß 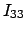 nicht von der
Zeit abhängt.
nicht von der
Zeit abhängt.
Ein physikalisches Pendel ist ein starrer Körper, der um eine waagrechte Achse (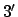 -Achse)
drehbar gelagert ist und sich unter dem Einfluß der Schwerkraft bewegt,
Abb. 9.11(b).
Das Trägheitsmoment ist:
-Achse)
drehbar gelagert ist und sich unter dem Einfluß der Schwerkraft bewegt,
Abb. 9.11(b).
Das Trägheitsmoment ist:
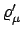 ist der Abstand der Masse
ist der Abstand der Masse 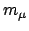 von der
von der 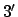 -Achse.
Für das Moment der Schwerkraft ergibt sich
-Achse.
Für das Moment der Schwerkraft ergibt sich
Die Bewegungsgleichung ist also gemäss Gl. (9.45)
Vergleich mit der Schwingungsgleichung für das mathematische Pendel, Gl. (3.14),
ergibt, daß ein mathematisches Pendel der Länge
(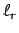 = reduzierte Pendellänge) gleiche Schwingungsdauer hat wie das
physikalische Pendel. Z.B. ist die Schwingungsdauer für einen Stab
(Abb. 9.9, Gl. (9.34)) für kleine Schwingungen
= reduzierte Pendellänge) gleiche Schwingungsdauer hat wie das
physikalische Pendel. Z.B. ist die Schwingungsdauer für einen Stab
(Abb. 9.9, Gl. (9.34)) für kleine Schwingungen
kürzer als die, Gl. (3.16), des mathematischen Pendels gleicher Länge.
Ein Kreisel ist ein starrer Körper, der in einem Punkt, dem Stützpunkt,
festgehalten ist und sich um diesen frei bewegen kann. Allgemeiner ist ein Kreisel
ein Körper, dessen Bewegung um einen Punkt (z.B. Schwerpunkt) von der Bewegung
dieses Punktes separiert werden kann. Der Kreisel hat daher 3 Freiheitsgrade,
wenn seine Bewegung nicht durch weitere Nebenbedingungen eingeschränkt ist. Das
dynamische Verhalten des Kreisels ist durch den zum Stützpunkt gehörigen
Trägheitstensor bestimmt. Die kinetische Energie ist gleich der Rotationsenergie,
Gl. (9.48).
Sind alle Hauptträgheitsmomente verschieden, heißt der Kreisel unsymmetrisch;
sind genau zwei gleich, heißt er symmetrisch; sind alle drei gleich, dann
spricht man von einem Kugelkreisel.
In der Beschreibung der Kreiselbewegung spielen der Drehimpulsvektor 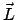 und
der Winkelgeschwindigkeitsvektor
und
der Winkelgeschwindigkeitsvektor
 eine wichtige Rolle. Die durch
eine wichtige Rolle. Die durch
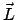 bestimmte Gerade heißt Drehimpulsachse; die durch
bestimmte Gerade heißt Drehimpulsachse; die durch
 gehende heißt momentane Drehachse.
gehende heißt momentane Drehachse.
Die zeitliche Änderung der Rotationsenergie (9.36) ist:
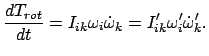 |
(946) |
Dabei wurde benützt, daß
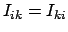 ist, daß
ist, daß
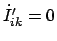 und daß
In der letzten Gleichung wurde die Transformationsformel für einen Tensor
zweiter Stufe verwendet und
und daß
In der letzten Gleichung wurde die Transformationsformel für einen Tensor
zweiter Stufe verwendet und
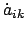 gemäß Gl. (8.29a) eliminiert.
Den gleichen Ausdruck wie auf der rechten Seite von (9.46) erhält man,
indem man Gl. (9.37) bzw. Gl. (9.43) mit
gemäß Gl. (8.29a) eliminiert.
Den gleichen Ausdruck wie auf der rechten Seite von (9.46) erhält man,
indem man Gl. (9.37) bzw. Gl. (9.43) mit
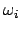 bzw.
bzw.
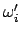 überschiebt; damit ergibt sich
überschiebt; damit ergibt sich
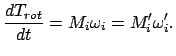 |
(947) |
Ein Kreisel heißt frei, wenn keine Kräfte auf ihn wirken. Im Schwerefeld kann
man einen solchen näherungsweise realisieren durch eine kardanische Aufhängung
oder durch eine solche Formgebung, daß der Schwerpunkt in der Spitze liegt, in
der der Kreisel gestützt ist, Abb. 9.12. Die Gesamtenergie ist gleich der
Rotationsenergie, Gl. (9.35), und ist eine Erhaltungsgröße
 const. const. |
(948) |
Dies folgt aus (9.47) oder aus dem entsprechenden Erhaltungssatz für
Vielteilchensysteme in Kap. 7; ebenso wie die Konstanz des Gesamtdrehimpulses
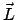 mit Benutzung von Gl. (9.37)
mit Benutzung von Gl. (9.37)
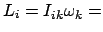 const. const. |
(949) |
Die Komponenten des Vektors der Winkelgeschwindigkeit
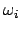 bzw.
bzw.
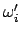 sind im allgemeinen nicht konstant. Das Zeitverhalten der körperfesten Komponenten
sind im allgemeinen nicht konstant. Das Zeitverhalten der körperfesten Komponenten
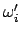 kann aus den Eulerschen Gleichungen (9.44) mit
kann aus den Eulerschen Gleichungen (9.44) mit
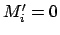 berechnet werden. Diese lassen sich unter Zuhilfenahme der Erhaltungssätze
für Energie und Drehimpuls exakt lösen; doch die Lösungen enthalten
elliptische Integrale und sind so kompliziert, daß man kaum Einblick
in die Natur der Bewegung erhalten kann. Diesen gewährt aber ein geometrisches
Konstruktionsverfahren von Poinsot.
berechnet werden. Diese lassen sich unter Zuhilfenahme der Erhaltungssätze
für Energie und Drehimpuls exakt lösen; doch die Lösungen enthalten
elliptische Integrale und sind so kompliziert, daß man kaum Einblick
in die Natur der Bewegung erhalten kann. Diesen gewährt aber ein geometrisches
Konstruktionsverfahren von Poinsot.
Man betrachtet einen Euklidischen Raum mit den kartesischen Koordinaten
 . Aus Gl. (9.48) folgt, daß in diesem Raum
die zu einer bestimmten Bewegung (zu einer bestimmten Energie
. Aus Gl. (9.48) folgt, daß in diesem Raum
die zu einer bestimmten Bewegung (zu einer bestimmten Energie 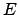 )
gehörige Menge der Werte
)
gehörige Menge der Werte
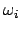 auf einem Ellipsoid mit der Gl. (9.48)
liegen, das zum Trägheitsellipsoid (9.28) ähnlich und koaxial ist. Aus
auf einem Ellipsoid mit der Gl. (9.48)
liegen, das zum Trägheitsellipsoid (9.28) ähnlich und koaxial ist. Aus
grad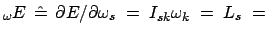 const. const. |
(950) |
folgt, daß der Drehimpulsvektor in jedem Augenblick parallel zur Flächennormalen
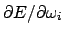 , also senkrecht zur Tangentialebene
, also senkrecht zur Tangentialebene  steht. Deswegen gilt die Poinsotsche Konstruktion (Abb. 9.13):
steht. Deswegen gilt die Poinsotsche Konstruktion (Abb. 9.13):
Man erhält die Richtung von 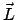 zu einem vorgegebenen
zu einem vorgegebenen
 ,
indem man an den durch
,
indem man an den durch
 bezeichneten Punkt des Poinsotschen
Ellipsoids die Tangentialebene
bezeichneten Punkt des Poinsotschen
Ellipsoids die Tangentialebene  legt und ihre Normalenrichtung einzeichnet.
Wegen der Erhaltung des Drehimpulses ist die Stellung von
legt und ihre Normalenrichtung einzeichnet.
Wegen der Erhaltung des Drehimpulses ist die Stellung von  im Raum
zeitlich konstant. Daher heißt sie invariable Ebene. Ihr Abstand vom
raumfesten Bezugspunkt 0 ist konstant, da alle während der Bewegung möglichen
im Raum
zeitlich konstant. Daher heißt sie invariable Ebene. Ihr Abstand vom
raumfesten Bezugspunkt 0 ist konstant, da alle während der Bewegung möglichen
 die gleiche Projektion auf die Normalenrichtung haben gemäß
den aus Gln. (9.48) und (9.49) folgenden Gleichungen:
die gleiche Projektion auf die Normalenrichtung haben gemäß
den aus Gln. (9.48) und (9.49) folgenden Gleichungen:
1cm
Abbildung:
Lagerung eines kräftefreien Kreisels im Schwerpunkt 
|
![\includegraphics[scale=1.15]{k9_kreisel}](img2254.gif)
|
Abbildung 9.13:
Poinsotsche Konstruktion
|
![\includegraphics[scale=0.52]{k9_poinsot}](img2255.gif)
|
Abbildung 9.14:
Polbahnen auf dem Poinsotschen Ellipsoid
|
![\includegraphics[scale=0.7]{k9_polbahn_ellipso}](img2256.gif)
|
Im Laufe der Bewegung des Körpers rollt das Poinsotsche Ellipsoid, das fest
mit dem Körper verbunden ist, gleitungsfrei auf der invariablen Ebene ab
(s. K9RollPoinsot.mov).
Der
Vektor vom zeitlich unveränderlichen Zentrum 0 der Ellipse zum
Berührungspunkt 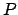 gibt immer die momentane Winkelgeschwindigkeit
gibt immer die momentane Winkelgeschwindigkeit
 an. Die Kurve, die von der Folge von Berührungspunkten auf
dem Ellipsoid erzeugt wird, heißt Polbahn (oder Polhodie).
Sie ist eine geschlossene Kurve, s. Abb. 9.14. Der Kegel, der von allen von
0 ausgehenden und durch die Polbahn gehenden Strahlen erzeugt
wird, heißt Polkegel. Die Bahn des Berührungspunktes
an. Die Kurve, die von der Folge von Berührungspunkten auf
dem Ellipsoid erzeugt wird, heißt Polbahn (oder Polhodie).
Sie ist eine geschlossene Kurve, s. Abb. 9.14. Der Kegel, der von allen von
0 ausgehenden und durch die Polbahn gehenden Strahlen erzeugt
wird, heißt Polkegel. Die Bahn des Berührungspunktes 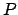 auf
der invariablen Ebene heißt Spurbahn (Herpolhodie) und
ist im allgemeinen nicht geschlossen. Sie bestimmt zusammen mit 0
den Spurkegel. Die Bewegung des Kreisels besteht also in diesem
geometrischen Bild in einem Abrollen des körperfesten Polkegels
auf dem raumfesten Spurkegel, da sich beide Kegel längs der momentanen
Drehachse berühren.
auf
der invariablen Ebene heißt Spurbahn (Herpolhodie) und
ist im allgemeinen nicht geschlossen. Sie bestimmt zusammen mit 0
den Spurkegel. Die Bewegung des Kreisels besteht also in diesem
geometrischen Bild in einem Abrollen des körperfesten Polkegels
auf dem raumfesten Spurkegel, da sich beide Kegel längs der momentanen
Drehachse berühren.
Dreht sich der Kreisel um eine seiner Hauptträgheitsachsen,
dann haben 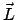 und
und
 gleiche Richtung, die Pol- und
Spurbahn entarten in einen Punkt auf einem der drei Scheitel
des Ellipsoides. Auch
gleiche Richtung, die Pol- und
Spurbahn entarten in einen Punkt auf einem der drei Scheitel
des Ellipsoides. Auch
 ist dann raumfest. Der Körper dreht
sich um eine freie Achse. Doch sind die drei Hauptträgheitsachsen
nicht gleichwertig. Die Drehung um die Achsen mit dem größten
und dem kleinsten Hauptträgheitsmoment ist stabil, die um
die Achse mit dem mittelgroßen Hauptträgheitsmoment ist instabil. Darunter
versteht man, daß eine Drehung, die anfänglich wenig von einer um eine
stabile Achse abweicht, für alle Zeiten sich nur wenig von der stabilen
unterscheidet; während eine anfängliche Drehung um eine instabile Achse
ihren Charakter sehr stark ändert.
ist dann raumfest. Der Körper dreht
sich um eine freie Achse. Doch sind die drei Hauptträgheitsachsen
nicht gleichwertig. Die Drehung um die Achsen mit dem größten
und dem kleinsten Hauptträgheitsmoment ist stabil, die um
die Achse mit dem mittelgroßen Hauptträgheitsmoment ist instabil. Darunter
versteht man, daß eine Drehung, die anfänglich wenig von einer um eine
stabile Achse abweicht, für alle Zeiten sich nur wenig von der stabilen
unterscheidet; während eine anfängliche Drehung um eine instabile Achse
ihren Charakter sehr stark ändert.
Dies ersieht man aus der Poinsotschen Darstellung: Eine Drehung, die sich nur
wenig von einer um die Achse mit größtem (kleinstem) Hauptträgheitsmoment
unterscheidet, hat eine Polkurve in der Nähe des Scheitels der längsten
(kleinsten) Hauptachse, s. Abb. 9.14. Die gemäß Gl. (9.49) zeitlich konstante
Projektion von
 auf die Drehimpulsachse ist größer
(kleiner) als die mittlere Halbachse und die Polkurve kann sich dem
mittleren Scheitel nicht nähern. Bei einer Drehung in der Nähe des
mittleren Scheitels ist eine solche Beschränkung nicht gegeben.
auf die Drehimpulsachse ist größer
(kleiner) als die mittlere Halbachse und die Polkurve kann sich dem
mittleren Scheitel nicht nähern. Bei einer Drehung in der Nähe des
mittleren Scheitels ist eine solche Beschränkung nicht gegeben.
Dieses Resultat kann man auch näherungweise aus den Eulerschen Gleichungen
ableiten. Die betrachtete freie Achse sei die 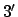 -Achse. Die Näherungsannahme,
daß die anfängliche Bewegung in deren Nähe erfolge, bedeutet, daß
-Achse. Die Näherungsannahme,
daß die anfängliche Bewegung in deren Nähe erfolge, bedeutet, daß
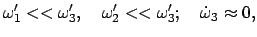
also
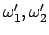 sehr klein sind. Dann ist die dritte
Eulersche Gleichung vernachlässigbar klein; die beiden ersten werden in
zwei äquivalente Differentialgleichungen zweiter Ordnung umgewandelt,
indem jeweils die eine nach der Zeit differenziert und in die zweite
eingesetzt wird. Dies gibt
sehr klein sind. Dann ist die dritte
Eulersche Gleichung vernachlässigbar klein; die beiden ersten werden in
zwei äquivalente Differentialgleichungen zweiter Ordnung umgewandelt,
indem jeweils die eine nach der Zeit differenziert und in die zweite
eingesetzt wird. Dies gibt
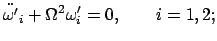
mit
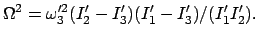
Ist 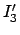 , das Hauptträgheitsmoment um die betrachtete freie Achse, das kleinste
oder das größte, dann ist
, das Hauptträgheitsmoment um die betrachtete freie Achse, das kleinste
oder das größte, dann ist
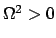 ; obige Differentialgleichungen
sind Schwingungsgleichungen; eine Lösung kleiner Amplitude bleibt klein. Liegt
dagegen
; obige Differentialgleichungen
sind Schwingungsgleichungen; eine Lösung kleiner Amplitude bleibt klein. Liegt
dagegen 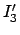 zwischen
zwischen  und
und 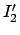 , dann ist
, dann ist
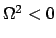 .
Die Lösungen obiger Differentialgleichungen enthalten Exponentialfunktion
.
Die Lösungen obiger Differentialgleichungen enthalten Exponentialfunktion
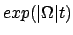 , sodaß die
, sodaß die
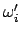 im Laufe der Zeit größer werden
können. Natürlich sind dann obige Näherungsannahmen nicht mehr erfüllt,
sodaß die Lösungen nur in der Nähe von
im Laufe der Zeit größer werden
können. Natürlich sind dann obige Näherungsannahmen nicht mehr erfüllt,
sodaß die Lösungen nur in der Nähe von
 gültig
sind.
gültig
sind.
Die Bewegung ist wesentlich einfacher, wenn der Kreisel symmetrisch ist.
Das Trägheitsellipsoid eines symmetrischen Kreisels ist ein Rotationsellipsoid.
Die der Symmetrieachse des Rotationsellipsoids (und auch des Körpers)
entsprechende Achse heißt Figurenachse. Sie wird zur 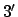 -Achse des
körperfesten Systems gewählt. Wir bezeichnen die körperfesten
Hauptträgheitsmomente
-Achse des
körperfesten Systems gewählt. Wir bezeichnen die körperfesten
Hauptträgheitsmomente
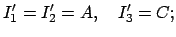 |
(952) |
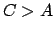 .... abgeplatteter Kreisel (E.: oblate top) (z.B. Scheibe senkrecht zu
.... abgeplatteter Kreisel (E.: oblate top) (z.B. Scheibe senkrecht zu 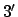 )
)
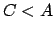 .... verlängerter Kreisel (E.: prolate top) (zigarrenförmig um
.... verlängerter Kreisel (E.: prolate top) (zigarrenförmig um 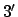 )
)
Die Poinsotsche Darstellung wird in diesem Fall noch wesentlich einfacher. Da
die Polbahn auf dem Poinsotschen Ellipsoid von den Punkten gebildet wird, die
von 0 konstante Entfernung haben, ist sie hier ein Kreis; der Polkegel ist
ein Kreiskegel mit der Figurenachse als Achse. Daher ist die Winkelgeschwindigkeit
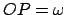 konstant. Ebenso besteht die Spurkurve aus allen Punkten der
invariablen Ebene, deren Entfernung von 0 konstant ist, und ist daher
gleichfalls ein Kreis. Der Spurkegel ist ein Kreiskegel mit der Drehimpulsachse
als Achse. Da der Polkegel auf dem Spurkegel abrollt, gilt also:
Die Figurenachse
konstant. Ebenso besteht die Spurkurve aus allen Punkten der
invariablen Ebene, deren Entfernung von 0 konstant ist, und ist daher
gleichfalls ein Kreis. Der Spurkegel ist ein Kreiskegel mit der Drehimpulsachse
als Achse. Da der Polkegel auf dem Spurkegel abrollt, gilt also:
Die Figurenachse 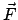 und die momentane Drehachse
und die momentane Drehachse
 beschreiben je einen Kreiskegel, und zwar mit konstanter Winkelgeschwindigkeit.
Die Bewegung der Figurenachse heißt
beschreiben je einen Kreiskegel, und zwar mit konstanter Winkelgeschwindigkeit.
Die Bewegung der Figurenachse heißt
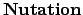 (manchmal auch reguläre
Präzession). Wegen der achsialen Symmetrie des Kreisels liegen die drei Achsen
immer in einer Ebene. Für die Reihenfolge der drei Achsen gibt es zwei
Möglichkeiten; diese sind in Abb. 9.15 und
Abb. 9.16 gezeigt.
(manchmal auch reguläre
Präzession). Wegen der achsialen Symmetrie des Kreisels liegen die drei Achsen
immer in einer Ebene. Für die Reihenfolge der drei Achsen gibt es zwei
Möglichkeiten; diese sind in Abb. 9.15 und
Abb. 9.16 gezeigt.
1cm
Abbildung 9.15:
 abgeplatteter Kreisel
abgeplatteter Kreisel
|
![\includegraphics[scale=0.76]{k9_abgeplattet_kreisel}](img2271.gif)
|
Abbildung:
 verlängerter Kreisel
verlängerter Kreisel
|
![\includegraphics[scale=0.76]{k9_langer_kreisel}](img2272.gif)
|
Für den symmetrischen Kreisel lassen sich die Eulerschen Gleichungen (9.44) sehr
einfach lösen. Mit den in Gl. (9.52) eingeführten Bezeichnungen werden die
Eulerschen Gleichungen
Aus der letzten Gleichung folgt die Konstanz von
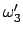 . Danach sind die
ersten zwei Gleichungen leicht zu lösen. Aus Gl. (9.14) erhält man die
Drehimpulskomponenten
. Danach sind die
ersten zwei Gleichungen leicht zu lösen. Aus Gl. (9.14) erhält man die
Drehimpulskomponenten
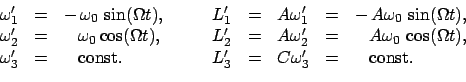 |
(954) |
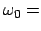 const., daher auch
const., daher auch
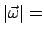 const.
Die Projektionen von
const.
Die Projektionen von
 und
und 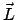 auf die
auf die
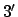 -Achse sind konstant. Beide Vektoren präzessieren mit der Frequenz
-Achse sind konstant. Beide Vektoren präzessieren mit der Frequenz
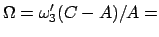 const. const. |
(955) |
auf Kegeln um die 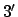 -Achse. Die halben Öffnungswinkel dieser Kegel sind
konstant und haben die Werte (s. Abb. 9.17):
-Achse. Die halben Öffnungswinkel dieser Kegel sind
konstant und haben die Werte (s. Abb. 9.17):
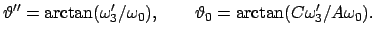 |
(956) |
Die Bewegung des Kreisels ist vollständig erfaßt, wenn man noch das
zeitliche Verhalten der Eulerschen Winkel (s. §8.3) angibt, die die
augenblickliche Lage des körperfesten Systems im Raum festlegen. Das
raumfeste System wird so orientiert, daß die 3-Achse mit dem
Drehimpulsvektor zusammenfällt. Der Winkel  zwischen
letzterem und der Figurenachse ist gemäß Gl. (9.54) konstant und hat den
in Gl. (9.56) angegebenen Wert
zwischen
letzterem und der Figurenachse ist gemäß Gl. (9.54) konstant und hat den
in Gl. (9.56) angegebenen Wert
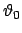 . Es werden die Ausdrücke
aus Gl. (8.31) in den Ausdruck für die kinetische Energie im
Hauptachsensystem eingesetzt
. Es werden die Ausdrücke
aus Gl. (8.31) in den Ausdruck für die kinetische Energie im
Hauptachsensystem eingesetzt
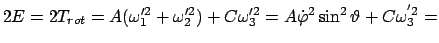 const. const. |
(957) |
Wegen
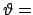 const. und
const. und
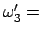 const. ist auch
const. ist auch
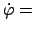 const.; damit ist wegen, s. (8.31),
const.; damit ist wegen, s. (8.31),
 const. const. |
(958) |
auch
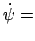 const. Vergleich der Ausdrücke für
const. Vergleich der Ausdrücke für
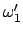 und
und
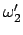 in Gl. (8.31) mit den entsprechenden Lösungen (9.54)
gibt für
in Gl. (8.31) mit den entsprechenden Lösungen (9.54)
gibt für  und
und 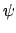
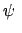 |
 |
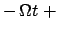 const. const. |
|
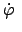 |
 |
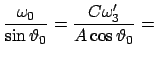 const. const.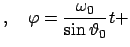 const. const. |
(959) |
Damit und mit Gl. (8.31) sind die Komponenten von
 im
raumfesten System gegeben:
im
raumfesten System gegeben:
 und
und 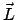 schließen den Winkel
schließen den Winkel
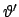 ein
ein
Dabei wurden Gln. (9.59) und (9.56) herangezogen. Die Stellung der Figurenachse ist
durch die der 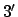 -Achse im Raum gegeben (Gl. (8.16d)):
Aus diesen Gleichungen folgt: Der Kreisel rotiert mit der Frequenz
-Achse im Raum gegeben (Gl. (8.16d)):
Aus diesen Gleichungen folgt: Der Kreisel rotiert mit der Frequenz
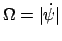 um seine Symmetrieachse (Figurenachse); letztere präzessiert
mit Frequenz
um seine Symmetrieachse (Figurenachse); letztere präzessiert
mit Frequenz
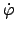 auf einem Kegel mit halbem Öffnungswinkel
auf einem Kegel mit halbem Öffnungswinkel
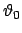 um die Drehimpuls-(3-Achse) (Nutation).
um die Drehimpuls-(3-Achse) (Nutation).
 liegt mit
liegt mit 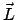 und der Figurenachse in einer Ebene und präzessiert
mit Frequenz
und der Figurenachse in einer Ebene und präzessiert
mit Frequenz
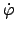 auf dem Spurkegel mit halbem Öffnungswinkel
auf dem Spurkegel mit halbem Öffnungswinkel
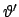 (Abb. 9.17).
(Abb. 9.17).
1cm
Abbildung 9.17:
Der freie symmetrische Kreisel
|
![\includegraphics[scale=0.8]{k9_freiersym_kreisel}](img2303.gif)
|
Abbildung 9.18:
Der schwere symmetrische Kreisel
|
![\includegraphics[scale=0.8]{k9_schw_sym_kreisel}](img2304.gif)
|
Wenn man in erster Näherung das Drehmoment, das Sonne und Mond auf den
äquatorialen Wulst der Erde ausüben, vernachlässigt, kann die Erde als ein
freier symmetrischer Kreisel behandelt werden. Aufgrund der Abplattung der
Erde ist
Danach sollte die momentane Drehachse im Lauf von 300 Tagen (= 10 Monaten)
einen Kreis um den Nordpol beschreiben. Es wurde eine stark fluktuierende
Bewegung mit einem Radius von nicht mehr als 4,5 m und einer Periode von 427
Tagen beobachtet (Chandlersche Periode). Daraus und aus Gl. (9.60) kann man
berechnen, daß Drehimpuls- und Figurenachse an den Polen einen Abstand
von maximal 1,5 cm haben,
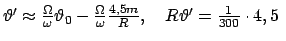 m
m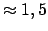 cm. Der Unterschied in der Periode kann erklärt werden,
wenn man annimmt, daß die Erdkugel nicht ideal starr ist, sondern elastische
Eigenschaften wie Stahl hat.
cm. Der Unterschied in der Periode kann erklärt werden,
wenn man annimmt, daß die Erdkugel nicht ideal starr ist, sondern elastische
Eigenschaften wie Stahl hat.
Dieser Kreisel ist nicht im Schwerpunkt gelagert. Die Gesamtmasse 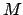 , die man
sich im Schwerpunkt
, die man
sich im Schwerpunkt  konzentriert denken kann, erzeugt ein Moment um die
Knotenachse (s. Abb. 9.18):
konzentriert denken kann, erzeugt ein Moment um die
Knotenachse (s. Abb. 9.18):
Da  der Winkel um die Knotenachse ist, kann man für dieses Moment
das folgende Potential einführen
der Winkel um die Knotenachse ist, kann man für dieses Moment
das folgende Potential einführen
 |
(961) |
Die kinetische Energie (= Rotationsenergie) berechnet man in den Eulerschen
Winkeln aus Gln. (9.57) und (8.31). Zusammen mit Gl. (9.61) gibt das die
Lagrangefunktion (vgl. §11.5):
In ihr sind  und
und 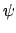 zyklische Koordinaten; daher sind die
kanonisch konjugierten Impulse zeitlich konstant (vgl. §12.4),
zyklische Koordinaten; daher sind die
kanonisch konjugierten Impulse zeitlich konstant (vgl. §12.4), 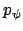 ist die Projektion von
ist die Projektion von 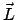 auf die
auf die 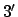 -Achse,
-Achse,
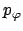 die auf die 3-Achse.
die auf die 3-Achse.
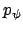 |
 |
 const. const. |
(963) |
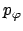 |
 |
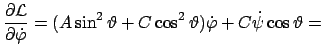 const. const. |
(964) |
| |
 |
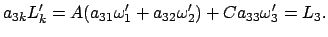 |
|
(Letzteres erkennt man aus Gln. (8.13) und (8.31). Diese beiden Impulse sind
erhalten, da die Knotenlinie, also auch das obige Moment des Schwerpunktes, auf
diesen beiden Achsen senkrecht steht. Obige Gleichungen werden nach
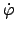 und
und
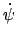 aufgelöst und geben:
aufgelöst und geben:
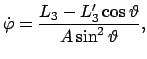 (a) (a)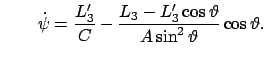 (b) (b) |
(965) |
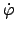 und
und
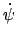 sind bekannt, sobald
sind bekannt, sobald  als Funktion
der Zeit bekannt ist. Letzteres Verhalten kann aus dem Energiesatz abgeleitet
werden. In diesem wird berücksichtigt, daß gemäß Gl. (9.63)
als Funktion
der Zeit bekannt ist. Letzteres Verhalten kann aus dem Energiesatz abgeleitet
werden. In diesem wird berücksichtigt, daß gemäß Gl. (9.63)
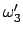 konstant ist;
konstant ist;
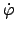 wird darin mittels Gl. (9.65) eliminiert
wird darin mittels Gl. (9.65) eliminiert
Die Substitution
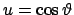 und Auflösen nach
und Auflösen nach 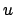 geben eine
Differentialgleichung für
geben eine
Differentialgleichung für 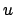 bzw.
bzw.
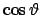 , die durch Separation
gelöst werden kann.
, die durch Separation
gelöst werden kann.
![$\displaystyle P(u) = (1-u^{2}) \left[ \frac{2EA}{L^{'2}_{3}} - \frac{A}{C} - \frac{2MgsA}{L_{3}^{'2}} u \right] - \left( \frac{L'_{3}}{L_{3}} - u \right)^{2}.$](img2330.gif) |
(967) |
Da 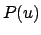 ein Polynom dritten Grades ist, ist das Integral in u elliptisch.
Man kann aber einen qualitativen Überblick über die Bewegungstypen erhalten,
indem man das Realitätsverhalten der Wurzel diskutiert, ähnlich wie beim
sphärischen Pendel in §6.3.1. Die Eulerschen Winkel
ein Polynom dritten Grades ist, ist das Integral in u elliptisch.
Man kann aber einen qualitativen Überblick über die Bewegungstypen erhalten,
indem man das Realitätsverhalten der Wurzel diskutiert, ähnlich wie beim
sphärischen Pendel in §6.3.1. Die Eulerschen Winkel  und
und
 geben die augenblickliche Lage des Punktes auf der Einheitskugel
um 0 an, in dem die Figurenachse diese durchstößt; dieser heißt der
Locus der Figurenachse. Wieder sind für die Bewegung nur die
Teilintervalle
geben die augenblickliche Lage des Punktes auf der Einheitskugel
um 0 an, in dem die Figurenachse diese durchstößt; dieser heißt der
Locus der Figurenachse. Wieder sind für die Bewegung nur die
Teilintervalle
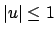 zulässig, in denen
zulässig, in denen
 ist. Wegen
ist. Wegen
ist eine Wurzel, 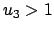 . Es können daher nur die beiden anderen,
. Es können daher nur die beiden anderen,
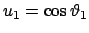 und
und
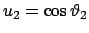 den
physikalischen Bereich begrenzen (Abb. 9.20(a)).
den
physikalischen Bereich begrenzen (Abb. 9.20(a)).  ist auf die
Kugelzone zwischen
ist auf die
Kugelzone zwischen
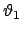 und
und
 beschränkt,
die Figurenachse präzessiert um die Vertikale. Diese Beschränkung
der Bewegung ist auch aus Gl. (9.66) abzulesen.
Für
beschränkt,
die Figurenachse präzessiert um die Vertikale. Diese Beschränkung
der Bewegung ist auch aus Gl. (9.66) abzulesen.
Für
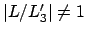 würde der Term
würde der Term
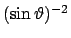 an
an
 unendlich werden. Aus Gl. (9.65a) ersieht man,
daß die Bewegung durch die Lage der Nullstelle
unendlich werden. Aus Gl. (9.65a) ersieht man,
daß die Bewegung durch die Lage der Nullstelle 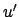 von
bestimmt wird. Liegt
von
bestimmt wird. Liegt 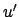 außerhalb
außerhalb
![$ [u_{1},u_{2}]$](img2349.gif) , dann wächst (oder
fällt)
, dann wächst (oder
fällt)
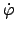 monoton (Abb. 9.19(a)); ist
monoton (Abb. 9.19(a)); ist
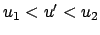 ,
dann ändert
,
dann ändert
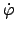 sein Vorzeichen, die Locuskurve hat Schleifen
(Abb. 9.19(b)). Fällt
sein Vorzeichen, die Locuskurve hat Schleifen
(Abb. 9.19(b)). Fällt 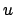 mit einer der Wurzeln
mit einer der Wurzeln 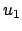 ,
, 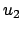 zusammen,
dann sind dort
zusammen,
dann sind dort
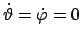 , die Locuskurve hat Spitzen.
Dies entspricht dem folgenden Fall: Zur Zeit
, die Locuskurve hat Spitzen.
Dies entspricht dem folgenden Fall: Zur Zeit 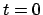 wird die Figurenachse
mit einer Anfangslage
wird die Figurenachse
mit einer Anfangslage
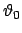 ausgelassen; Anfangsbedingungen sind
dann:
ausgelassen; Anfangsbedingungen sind
dann:
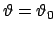 ,
,
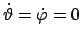 .
Es ist
.
Es ist
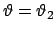 , und entspricht dem oberen Begrenzungskreis,
denn sobald
, und entspricht dem oberen Begrenzungskreis,
denn sobald
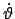 und
und
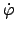 von Null weggehen, nimmt
die (positive) kinetische Energie zu, die potentielle muß abnehmen, also
muß
von Null weggehen, nimmt
die (positive) kinetische Energie zu, die potentielle muß abnehmen, also
muß  von
von
 gegen
gegen 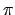 gehen; die Kreiselachse
kippt, bis der Grenzwinkel
gehen; die Kreiselachse
kippt, bis der Grenzwinkel
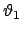 erreicht ist, dann strebt sie
wieder gegen
erreicht ist, dann strebt sie
wieder gegen
 (Abb. 9.19(c)).
(Abb. 9.19(c)).
Abbildung:
Locuskurve für die Bewegung des schweren symmetrischen Kreisels
|
![\includegraphics[scale=1.1]{k9_locuskurve}](img2356.gif) |
Abbildung:
Links: a) Bewegung mit Nutationen wie in Abb. 9.19. Rechts:
b) Reguläre Präcession, keine Nutationen.
|
|
Falls
 ist, kann der obere (untere) Grenzkreis auf
den Nordpol (Südpol) zusammenschrumpfen. Wenn die beiden Grenzkreise
zusammenfallen,
ist, kann der obere (untere) Grenzkreis auf
den Nordpol (Südpol) zusammenschrumpfen. Wenn die beiden Grenzkreise
zusammenfallen,
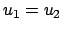 , treten keine Nutationen auf, der Kreisel
führt eine reguläre Präzession aus.
, treten keine Nutationen auf, der Kreisel
führt eine reguläre Präzession aus. 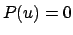 muß dann eine
Doppelwurzel haben (Abb. 9.20(b)). Diese findet man leichter, indem man Gl. (9.66)
nach
muß dann eine
Doppelwurzel haben (Abb. 9.20(b)). Diese findet man leichter, indem man Gl. (9.66)
nach  differenziert und
differenziert und
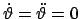 ,
,
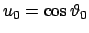 verlangt. Dies gibt
verlangt. Dies gibt
| |
|
![$\displaystyle \dot{\vartheta} \bigg[\ddot{\vartheta} -
\frac{\cos\vartheta_0}...
...3 - L'_3 \cos\vartheta_0\big)
- \frac{Mgs}{A} \sin\vartheta_0 \bigg] = 0.$](img2362.gif) |
|
| |
|
 |
(968) |
Zur Berechnung der 2. und 3. Gleichung wurde Gl. (9.63) benützt. Aus Gln. (9.68)
folgt, daß
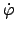 und
und
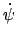 konstant sind. Sie müssen
zusammen mit
konstant sind. Sie müssen
zusammen mit
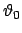 die obigen Bedingungen erfüllen.
die obigen Bedingungen erfüllen.
Eine Näherungslösung mit elementaren Funktionen kann erhalten werden, falls
die kinetische Energie der Rotation des Kreisels um die Figurenachse groß ist
im Vergleich zur Änderung der potentiellen Energie,
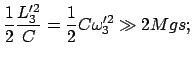 |
(969) |
dann sind die Wirkungen des Gravitationsmomentes, nämlich die Präzession
und die sie begleitende Nutation, nur kleine Störungen der vorherrschenden Rotation
des Kreisels um seine Figurenachse (''Schneller Kreisel'', pseudoreguläre
Präzession).
Ein interessanter Fall entspricht der Wurzel 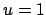 von
von 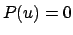 . Der Kreisel
steht am Anfang vertikal
. Der Kreisel
steht am Anfang vertikal
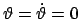 ; daraus folgt
die Gleichheit der Komponenten
; daraus folgt
die Gleichheit der Komponenten  und
und 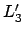 ; weiters folgt aus Gln. (9.66)
und (9.67)
; weiters folgt aus Gln. (9.66)
und (9.67)
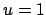 ist immer Doppelwurzel, die dritte Wurzel ist
ist immer Doppelwurzel, die dritte Wurzel ist
Abbildung 9.21:
Links: a) Schneller Kreisel (
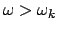 ) bleibt aufrecht. Rechts:
b) Langsamer Kreisel (
) bleibt aufrecht. Rechts:
b) Langsamer Kreisel (
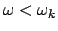 ) taumelt.
) taumelt.
|
|
Für 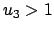 , (d.h.
, (d.h.
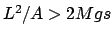 , und das entspricht ungefähr der
Bedingung, Gl. (9.69), für einen schnellen Kreisel) ist die einzige Möglichkeit
, und das entspricht ungefähr der
Bedingung, Gl. (9.69), für einen schnellen Kreisel) ist die einzige Möglichkeit
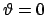 (Abb. 9.21(a)). Für
(Abb. 9.21(a)). Für 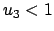 hat die Kurve die
in Abb. 9.21(b) gezeigte Gestalt, der Kreisel nutiert zwischen
hat die Kurve die
in Abb. 9.21(b) gezeigte Gestalt, der Kreisel nutiert zwischen
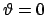 und
und
und
und
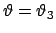 .
.
Es gibt eine kritische Winkelgeschwindigkeit
oberhalb derer nur Rotation um die Vertikale möglich ist. Wenn die Drehachse
des Kreisels anfangs vertikal steht und seine Winkelgeschwindigkeit 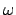 größer als
größer als
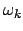 ist, dann dreht er sich für einige Zeit nur um die
Vertikale; durch die Reibung nimmt aber
ist, dann dreht er sich für einige Zeit nur um die
Vertikale; durch die Reibung nimmt aber 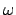 ab und der Kreisel beginnt
zu taumeln, sobald
ab und der Kreisel beginnt
zu taumeln, sobald
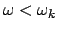 geworden ist.
geworden ist.
Christian Sommer
2003-01-27
![]() dieses
Körpers beschrieben.
Da die relativen Abstände der drei Punkte konstant sind, bleiben
9 Koordinaten - 3 Nebenbedingungen = 6 Freiheitsgrade.
Zu dieser Zahl kommt man auch über folgende geometrische Überlegung:
Die Bewegung des ersten Punktes, die Translation genannt wird, wird
durch 3 Parameter angegeben.
dieses
Körpers beschrieben.
Da die relativen Abstände der drei Punkte konstant sind, bleiben
9 Koordinaten - 3 Nebenbedingungen = 6 Freiheitsgrade.
Zu dieser Zahl kommt man auch über folgende geometrische Überlegung:
Die Bewegung des ersten Punktes, die Translation genannt wird, wird
durch 3 Parameter angegeben.
![]() kann sich nur mehr auf der Oberfläche der Kugel vom Radius
kann sich nur mehr auf der Oberfläche der Kugel vom Radius
![]() bewegen; dies gibt zwei weitere Parameter.
bewegen; dies gibt zwei weitere Parameter.
![]() kann sich nur mehr auf
einem Kreis (von gegebenem Radius) in einer Ebene senkrecht zur Verbindungsachse
von
kann sich nur mehr auf
einem Kreis (von gegebenem Radius) in einer Ebene senkrecht zur Verbindungsachse
von
![]() und
und
![]() bewegen; dies wird durch den 6. Parameter beschrieben.
bewegen; dies wird durch den 6. Parameter beschrieben.
![]() ) als Bezugspunkt.
Die Translation entspricht dem Verbindungsvektor von der Anfangslage
) als Bezugspunkt.
Die Translation entspricht dem Verbindungsvektor von der Anfangslage
![]() zur Endlage
zur Endlage
![]() . Die Bewegung der
übrigen Punkte des Körpers, also insbesondere von
. Die Bewegung der
übrigen Punkte des Körpers, also insbesondere von
![]() und
und
![]() wird durch ebendieselbe Translation plus eine
Drehung um eine durch
wird durch ebendieselbe Translation plus eine
Drehung um eine durch
![]() gehende Achse wiedergegeben.
Translationsvektor und Drehvektor enthalten je 3 Parameter; dies gibt wieder
die vorerwähnten 6 Freiheitsgrade.
gehende Achse wiedergegeben.
Translationsvektor und Drehvektor enthalten je 3 Parameter; dies gibt wieder
die vorerwähnten 6 Freiheitsgrade.
![]() ,
,
![]() ,
,
![]() und ihre Geschwindigkeiten
und ihre Geschwindigkeiten
![]() ,
,
![]() ,
,
![]() . Da
. Da
![]() als
Bezugspunkt gewählt worden ist, ist
als
Bezugspunkt gewählt worden ist, ist
![]() die
Translationsgeschwindigkeit. Für Punkt
die
Translationsgeschwindigkeit. Für Punkt
![]() gilt
gilt
![]() auf
auf
![]() senkrecht steht, kann man einen Drehvektor
einführen (Abb. 9.2):
senkrecht steht, kann man einen Drehvektor
einführen (Abb. 9.2):
![\includegraphics[scale=0.7]{k9_dreipkt_starr_k}](img2001.gif)
![\includegraphics[scale=0.7]{k9_winkgeschw_starr_k}](img2003.gif)
![]() ist für alle Punkte des
Körpers gleich.
ist für alle Punkte des
Körpers gleich.
![]() gelten analoge Berechnungen wie in Gl. (9.2),
sodaß wir wieder wie in Gl. (9.3) einen Drehvektor
gelten analoge Berechnungen wie in Gl. (9.2),
sodaß wir wieder wie in Gl. (9.3) einen Drehvektor
![]() einführen können.
einführen können.
![]() ,
,
![]() ,
,
![]() in weitem Maße
beliebig sind, kann immer erreicht werden, daß ihre Kombination in den
vorhergehenden Ausdrücken ungleich Null und nicht normal zu
in weitem Maße
beliebig sind, kann immer erreicht werden, daß ihre Kombination in den
vorhergehenden Ausdrücken ungleich Null und nicht normal zu
![]() ist. Also muß diese Differenz der
Winkelgeschwindigkeitsvektoren Null sein.
ist. Also muß diese Differenz der
Winkelgeschwindigkeitsvektoren Null sein.
![]() ist unabhängig vom Bezugspunkt;
also nur durch die Bewegung charakterisiert.
ist unabhängig vom Bezugspunkt;
also nur durch die Bewegung charakterisiert.
![]() als Bezugspunkt muß eine Gleichung analog zu (9.3) gelten.
Wir nehmen an, die zugehörige Winkelgeschwindigkeit sei
als Bezugspunkt muß eine Gleichung analog zu (9.3) gelten.
Wir nehmen an, die zugehörige Winkelgeschwindigkeit sei
![]() und
setzen dann Gln. (9.3), (9.4), (9.5) ein.
und
setzen dann Gln. (9.3), (9.4), (9.5) ein.
![]() Bezugspunkt:
Bezugspunkt:
![]() läßt sich aus der Geschwindigkeit dreier
Punkte des Körpers berechnen., (Gl. (9.6)).
läßt sich aus der Geschwindigkeit dreier
Punkte des Körpers berechnen., (Gl. (9.6)).
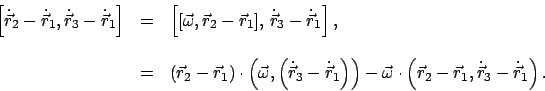
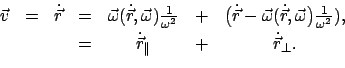
![]() , der durch die folgenden zwei
Bedingungen festgelegt ist
, der durch die folgenden zwei
Bedingungen festgelegt ist
![$\displaystyle \dot{\vec r} - \vec{\omega}(\vec{\omega},\dot{\vec r}) \frac{1}{{...
...r}_{1} - \vec{r}] \quad \wedge \quad (\vec{\omega},\vec{r}_{1} - \vec{r})
= 0.
$](img2029.gif)
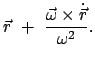
![$\displaystyle \dot{\vec r}_{1} = \dot{\vec r} + [\vec{\omega},\vec{r}_{1}-\vec{...
...\frac{\vec{\omega} \times \dot{\vec r}}
{\omega^{2}} \right ] \right)}_{= 0} .
$](img2034.gif)
![\includegraphics[scale=0.83]{k9_rot_trans_zyl}](img2043.gif)
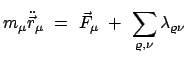 grad
grad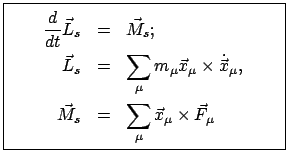
![$\displaystyle \sum_{\mu} \left[ \vec{r}_{s}+\vec{x}_{\mu}, m_{\mu}
\dot{\vec r}_{s}+m_{\mu}\dot{\vec x}_{\mu} \right],$](img2067.gif)
![$\displaystyle M \left[\vec{r}_{s}, \dot{\vec r}_{s} \right] +
\Big[\vec{r}_{s},...
...{\mu}}_
{= 0} \Big] + \sum_{\mu} m_{\mu} [\vec{x}_{\mu}, \dot{\vec x}_{\mu} ] .$](img2068.gif)
![$\displaystyle \sum_{\mu} [\vec{r}_{s}+\vec{x}_{\mu}, \vec{F}_{\mu} ]$](img2070.gif)
![$\displaystyle [\vec{r}_{s}, \sum_{\mu} \vec{F}_{\mu} ] + \vec{M}_{s} =
\dot{\vec L} = M[\vec{r}_{s}, \ddot{\vec r}_{s} ] + \frac{d}{dt} \vec{L}_{s} .$](img2071.gif)

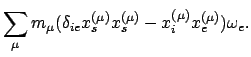
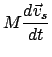
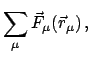
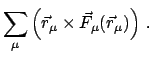
![]() nur im Schwerpunkt
nur im Schwerpunkt ![]() angreift. Die Rektionskräfte
angreift. Die Rektionskräfte ![]() ,
, ![]() und die
Reibungskräfte
und die
Reibungskräfte ![]() ,
, ![]() wirken nur an den Endpunkten. Die Kräfte
und ihre Kraftarme sind
wirken nur an den Endpunkten. Die Kräfte
und ihre Kraftarme sind
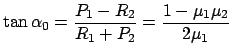
![]() ,
die Elemente der Hauptdiagonale, heißen Trägheitsmomente;
,
die Elemente der Hauptdiagonale, heißen Trägheitsmomente; ![]() ,
die Elemente außerhalb der Hauptdiagonalen, heißen Deviationsmomente.
Die Bedeutung dieser Namen wird unten erläutert.
,
die Elemente außerhalb der Hauptdiagonalen, heißen Deviationsmomente.
Die Bedeutung dieser Namen wird unten erläutert.
![]() beschriebene
Massenverteilung, hat man statt (9.23)
beschriebene
Massenverteilung, hat man statt (9.23)
![]() heißen die Hauptträgheitsmomente; sie sind immer positiv (Beweis
am Ende dieses §).
heißen die Hauptträgheitsmomente; sie sind immer positiv (Beweis
am Ende dieses §).
![]() mit Punkten (oder Vektoren)
mit Punkten (oder Vektoren)
![]() heran. In diesem Raum
stellt der Ausdruck
heran. In diesem Raum
stellt der Ausdruck
![\includegraphics[scale=0.63]{k9_treagheits_ellipso}](img2127.gif) []
[]
![\includegraphics[scale=0.54]{k9_versch_treagh_ell}](img2128.gif)
![]() ).
).
![]() seien die
Koordinaten des Punktes
seien die
Koordinaten des Punktes
![]() bezüglich S, Abb. 9.7.
bezüglich S, Abb. 9.7.
![$\displaystyle \hspace*{-0.65cm} I_{ik}\;\; =\;\; \sum_{\mu} m_{\mu} \left[ (s_{...
...{(\mu)})
\delta_{ik}\; -\; (s_{i}+r_{i}^{(\mu)})(s_{k}+r_{k}^{(\mu)}) \right];
$](img2140.gif)

![]() gegeben:
gegeben:
![]() ist der Winkel zwischen dem Vektor
ist der Winkel zwischen dem Vektor ![]() der Drehachse und der
der Drehachse und der
![]() -ten Hauptträgheitsachse. Dann bekommen wir
-ten Hauptträgheitsachse. Dann bekommen wir
![]() und
und ![]() und bekommen
und bekommen
![\includegraphics[scale=0.63]{k9_steiner_satz}](img2157.gif)
![\includegraphics[scale=0.63]{k9_drehung_stab}](img2158.gif)
![\includegraphics[scale=0.63]{k9_drehung_rechteck}](img2159.gif)
![]() , Länge
, Länge ![]() ) für Rotation um
eine Achse senkrecht durch einen Endpunkt (Abb. 9.9) ist nach (9.32)
) für Rotation um
eine Achse senkrecht durch einen Endpunkt (Abb. 9.9) ist nach (9.32)
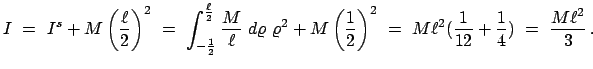
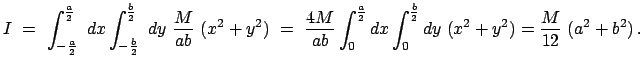
![]() ) und in eine Rotation gegeben durch den Drehvektor
) und in eine Rotation gegeben durch den Drehvektor
![]() .
Die Bewegung des Punktes
.
Die Bewegung des Punktes
![]() ist (vgl. Gl. (9.13))
ist (vgl. Gl. (9.13))
![]() wird daraus wegen Gln. (9.30)
und (9.31)
wird daraus wegen Gln. (9.30)
und (9.31)
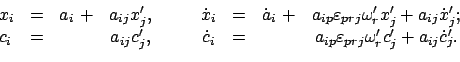
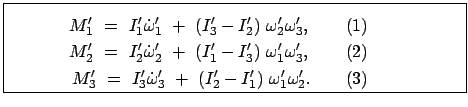
![]() nichtlinearen Terme entsprechen dem Moment der Zentrifugalkraft.
nichtlinearen Terme entsprechen dem Moment der Zentrifugalkraft.
![]()
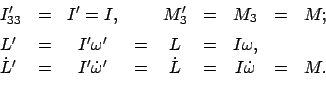
![]() .
Daß Gln. (9.45) auch im raumfesten System gelten, sieht man durch Transformation
ins raumfeste System. Dabei ergibt sich auch noch, daß
.
Daß Gln. (9.45) auch im raumfesten System gelten, sieht man durch Transformation
ins raumfeste System. Dabei ergibt sich auch noch, daß ![]() nicht von der
Zeit abhängt.
nicht von der
Zeit abhängt.
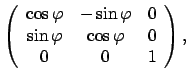
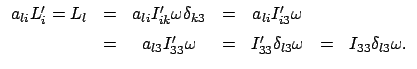
![]() -Achse)
drehbar gelagert ist und sich unter dem Einfluß der Schwerkraft bewegt,
Abb. 9.11(b).
Das Trägheitsmoment ist:
-Achse)
drehbar gelagert ist und sich unter dem Einfluß der Schwerkraft bewegt,
Abb. 9.11(b).
Das Trägheitsmoment ist:
![$\displaystyle \vec{M} = \sum_{\mu} \left[\vec{r}_{\mu}, \vec{F}_{\mu} \right] =
\sum_{\mu} \left[\vec{r}_{\mu}, gm_{\mu}\vec{e}_{1}\right]$](img2225.gif)
![$\displaystyle g \left[ \sum_{\mu} m_{\mu} \vec{r}_{\mu}, \vec{e}_{1} \right]$](img2226.gif)
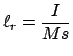
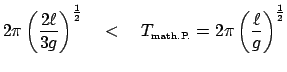
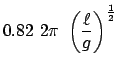
![]() und
der Winkelgeschwindigkeitsvektor
und
der Winkelgeschwindigkeitsvektor
![]() eine wichtige Rolle. Die durch
eine wichtige Rolle. Die durch
![]() bestimmte Gerade heißt Drehimpulsachse; die durch
bestimmte Gerade heißt Drehimpulsachse; die durch
![]() gehende heißt momentane Drehachse.
gehende heißt momentane Drehachse.
![\includegraphics[scale=1.15]{k9_kreisel}](img2254.gif)
![\includegraphics[scale=0.52]{k9_poinsot}](img2255.gif)
![\includegraphics[scale=0.7]{k9_polbahn_ellipso}](img2256.gif)
![]() gibt immer die momentane Winkelgeschwindigkeit
gibt immer die momentane Winkelgeschwindigkeit
![]() an. Die Kurve, die von der Folge von Berührungspunkten auf
dem Ellipsoid erzeugt wird, heißt Polbahn (oder Polhodie).
Sie ist eine geschlossene Kurve, s. Abb. 9.14. Der Kegel, der von allen von
0 ausgehenden und durch die Polbahn gehenden Strahlen erzeugt
wird, heißt Polkegel. Die Bahn des Berührungspunktes
an. Die Kurve, die von der Folge von Berührungspunkten auf
dem Ellipsoid erzeugt wird, heißt Polbahn (oder Polhodie).
Sie ist eine geschlossene Kurve, s. Abb. 9.14. Der Kegel, der von allen von
0 ausgehenden und durch die Polbahn gehenden Strahlen erzeugt
wird, heißt Polkegel. Die Bahn des Berührungspunktes ![]() auf
der invariablen Ebene heißt Spurbahn (Herpolhodie) und
ist im allgemeinen nicht geschlossen. Sie bestimmt zusammen mit 0
den Spurkegel. Die Bewegung des Kreisels besteht also in diesem
geometrischen Bild in einem Abrollen des körperfesten Polkegels
auf dem raumfesten Spurkegel, da sich beide Kegel längs der momentanen
Drehachse berühren.
auf
der invariablen Ebene heißt Spurbahn (Herpolhodie) und
ist im allgemeinen nicht geschlossen. Sie bestimmt zusammen mit 0
den Spurkegel. Die Bewegung des Kreisels besteht also in diesem
geometrischen Bild in einem Abrollen des körperfesten Polkegels
auf dem raumfesten Spurkegel, da sich beide Kegel längs der momentanen
Drehachse berühren.
![]() und
und
![]() gleiche Richtung, die Pol- und
Spurbahn entarten in einen Punkt auf einem der drei Scheitel
des Ellipsoides. Auch
gleiche Richtung, die Pol- und
Spurbahn entarten in einen Punkt auf einem der drei Scheitel
des Ellipsoides. Auch
![]() ist dann raumfest. Der Körper dreht
sich um eine freie Achse. Doch sind die drei Hauptträgheitsachsen
nicht gleichwertig. Die Drehung um die Achsen mit dem größten
und dem kleinsten Hauptträgheitsmoment ist stabil, die um
die Achse mit dem mittelgroßen Hauptträgheitsmoment ist instabil. Darunter
versteht man, daß eine Drehung, die anfänglich wenig von einer um eine
stabile Achse abweicht, für alle Zeiten sich nur wenig von der stabilen
unterscheidet; während eine anfängliche Drehung um eine instabile Achse
ihren Charakter sehr stark ändert.
ist dann raumfest. Der Körper dreht
sich um eine freie Achse. Doch sind die drei Hauptträgheitsachsen
nicht gleichwertig. Die Drehung um die Achsen mit dem größten
und dem kleinsten Hauptträgheitsmoment ist stabil, die um
die Achse mit dem mittelgroßen Hauptträgheitsmoment ist instabil. Darunter
versteht man, daß eine Drehung, die anfänglich wenig von einer um eine
stabile Achse abweicht, für alle Zeiten sich nur wenig von der stabilen
unterscheidet; während eine anfängliche Drehung um eine instabile Achse
ihren Charakter sehr stark ändert.
![]() auf die Drehimpulsachse ist größer
(kleiner) als die mittlere Halbachse und die Polkurve kann sich dem
mittleren Scheitel nicht nähern. Bei einer Drehung in der Nähe des
mittleren Scheitels ist eine solche Beschränkung nicht gegeben.
auf die Drehimpulsachse ist größer
(kleiner) als die mittlere Halbachse und die Polkurve kann sich dem
mittleren Scheitel nicht nähern. Bei einer Drehung in der Nähe des
mittleren Scheitels ist eine solche Beschränkung nicht gegeben.
![]() -Achse. Die Näherungsannahme,
daß die anfängliche Bewegung in deren Nähe erfolge, bedeutet, daß
-Achse. Die Näherungsannahme,
daß die anfängliche Bewegung in deren Nähe erfolge, bedeutet, daß
![]() -Achse des
körperfesten Systems gewählt. Wir bezeichnen die körperfesten
Hauptträgheitsmomente
-Achse des
körperfesten Systems gewählt. Wir bezeichnen die körperfesten
Hauptträgheitsmomente
![]() .... abgeplatteter Kreisel (E.: oblate top) (z.B. Scheibe senkrecht zu
.... abgeplatteter Kreisel (E.: oblate top) (z.B. Scheibe senkrecht zu ![]() )
)
![]() .... verlängerter Kreisel (E.: prolate top) (zigarrenförmig um
.... verlängerter Kreisel (E.: prolate top) (zigarrenförmig um ![]() )
)
![]() konstant. Ebenso besteht die Spurkurve aus allen Punkten der
invariablen Ebene, deren Entfernung von 0 konstant ist, und ist daher
gleichfalls ein Kreis. Der Spurkegel ist ein Kreiskegel mit der Drehimpulsachse
als Achse. Da der Polkegel auf dem Spurkegel abrollt, gilt also:
Die Figurenachse
konstant. Ebenso besteht die Spurkurve aus allen Punkten der
invariablen Ebene, deren Entfernung von 0 konstant ist, und ist daher
gleichfalls ein Kreis. Der Spurkegel ist ein Kreiskegel mit der Drehimpulsachse
als Achse. Da der Polkegel auf dem Spurkegel abrollt, gilt also:
Die Figurenachse ![]() und die momentane Drehachse
und die momentane Drehachse
![]() beschreiben je einen Kreiskegel, und zwar mit konstanter Winkelgeschwindigkeit.
Die Bewegung der Figurenachse heißt
beschreiben je einen Kreiskegel, und zwar mit konstanter Winkelgeschwindigkeit.
Die Bewegung der Figurenachse heißt
![]() (manchmal auch reguläre
Präzession). Wegen der achsialen Symmetrie des Kreisels liegen die drei Achsen
immer in einer Ebene. Für die Reihenfolge der drei Achsen gibt es zwei
Möglichkeiten; diese sind in Abb. 9.15 und
Abb. 9.16 gezeigt.
(manchmal auch reguläre
Präzession). Wegen der achsialen Symmetrie des Kreisels liegen die drei Achsen
immer in einer Ebene. Für die Reihenfolge der drei Achsen gibt es zwei
Möglichkeiten; diese sind in Abb. 9.15 und
Abb. 9.16 gezeigt.
![]() , die man
sich im Schwerpunkt
, die man
sich im Schwerpunkt ![]() konzentriert denken kann, erzeugt ein Moment um die
Knotenachse (s. Abb. 9.18):
konzentriert denken kann, erzeugt ein Moment um die
Knotenachse (s. Abb. 9.18):
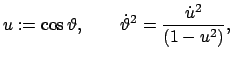
![\includegraphics[width=16cm]{K9A2021}](img2357.gif)
![]() ist, kann der obere (untere) Grenzkreis auf
den Nordpol (Südpol) zusammenschrumpfen. Wenn die beiden Grenzkreise
zusammenfallen,
ist, kann der obere (untere) Grenzkreis auf
den Nordpol (Südpol) zusammenschrumpfen. Wenn die beiden Grenzkreise
zusammenfallen,
![]() , treten keine Nutationen auf, der Kreisel
führt eine reguläre Präzession aus.
, treten keine Nutationen auf, der Kreisel
führt eine reguläre Präzession aus. ![]() muß dann eine
Doppelwurzel haben (Abb. 9.20(b)). Diese findet man leichter, indem man Gl. (9.66)
nach
muß dann eine
Doppelwurzel haben (Abb. 9.20(b)). Diese findet man leichter, indem man Gl. (9.66)
nach ![]() differenziert und
differenziert und
![]() ,
,
![]() verlangt. Dies gibt
verlangt. Dies gibt

![$\displaystyle (1-u^{2})(1-u) \frac{2AMgs}{L^{2}_{3}} - (1-u)^{2} \; =\; \
(1-u)^{2} \left[(1+u)\frac{2AMgs}{L^{2}_{3}} - 1 \right]$](img2370.gif)
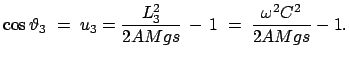
![\includegraphics[width=16cm]{K9A2223}](img2372.gif)
![]() , (d.h.
, (d.h.
![]() , und das entspricht ungefähr der
Bedingung, Gl. (9.69), für einen schnellen Kreisel) ist die einzige Möglichkeit
, und das entspricht ungefähr der
Bedingung, Gl. (9.69), für einen schnellen Kreisel) ist die einzige Möglichkeit
![]() (Abb. 9.21(a)). Für
(Abb. 9.21(a)). Für ![]() hat die Kurve die
in Abb. 9.21(b) gezeigte Gestalt, der Kreisel nutiert zwischen
hat die Kurve die
in Abb. 9.21(b) gezeigte Gestalt, der Kreisel nutiert zwischen
![]() und
und
und
und
![]() .
.
